4.1: Geometría, límites y continuidad

En este capítulo trataremos el caso general de una función mapeando\(\mathbb{R}^m\) a\(\mathbb{R}^n\). Desde los casos\(m=1\) y se\(n=1\) han manejado en capítulos anteriores, nuestro énfasis estará en los casos de dimensiones superiores, lo más importante cuando\(m\) y\(n\) son 2 o 3. Comenzaremos en esta sección con alguna terminología básica y definiciones.

Superficies parametrizadas

Si\(f: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\) tiene dominio\(D\), llamamos al conjunto\(S\) de todos los puntos\(\mathbf{y}\) en\(\mathbb{R}^n\) para los cuales\(\mathbf{y}=f(\mathbf{x})\) para algunos\(\mathbf{x}\) en\(D\) la imagen de \(f\). Es decir,

\[ S=\{f(\mathbf{x}): \mathbf{x} \in D\} ,\]

que es lo mismo que lo que antes hemos llamado el rango de\(f\). Si\(m=1\),\(S\) es una curva como se define en la Sección 2.1. Si\(m>1\) y\(n>m\), entonces llamamos\(S\) una superficie\(m\) -dimensional en\(\mathbb{R}^{n}\). Si dejamos\(\mathbf{x}=\left(x_{1}, x_{2}, \ldots, x_{m}\right)\) y\(\left(y_{1}, y_{2}, \ldots, y_{n}\right)=f\left(x_{1}, x_{2}, \ldots, x_{m}\right)\), entonces, for\(k=1,2, \ldots, n\), llamamos a la función\(f_{k}: \mathbb{R}^{n} \rightarrow \mathbb{R}\) definida por

\[ f_{k}\left(x_{1}, x_{2}, \ldots, x_{m}\right)=y_{k} \nonumber \]

la\(k\) -ésima función de coordenadas de\(f\). Llamamos al sistema de ecuaciones

\ [\ begin {align}
y_ {1} &=f_ {1}\ izquierda (x_ {1}, x_ {2},\ ldots, x_ {m}\ derecha),\ nonumber\\
y_ {2} &=f_ {2}\ izquierda (x_ {1}, x_ {2},\ ldots, x_ {m}\ derecha),\ nonumber\\
\ vdots &=\ quad\ vdots\ label {}\\
y_ {n} &=f_ {n}\ left (x_ {1}, x_ {2},\ ldots, x_ {m}\ derecha),\ nonumber
\ end {align}\]

una parametrización de la superficie\(S\). Obsérvese que\(f_k\) es el tipo de función que estudiamos en el Capítulo 3. Por otro lado, si fijamos valores de\(x_i\) para todos\(i \neq k\), entonces la función\(\varphi_{k}: \mathbb{R} \rightarrow \mathbb{R}^{n}\) definida por

\[ \varphi_{k}(t)=f\left(x_{1}, x_{2}, \ldots, x_{k-1}, t, x_{k+1}, \ldots, x_{m}\right) \]

es del tipo que estudiamos nosotros Capítulo 2. En particular, para cada\(k=1,2, \ldots, n, \varphi_{k}\) parametriza una curva que se encuentra en la superficie\(S\). Los siguientes ejemplos ilustran cómo este último comentario es útil cuando se intenta imaginar una superficie parametrizada\(S\).

Ejemplo\(\PageIndex{1}\)

Considerar\(f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{3}\) definido por

\[ f(s, t)=(t \cos (s), t \sin (s), t) \nonumber \]

para\(0 \leq s \leq 2 \pi\) y\(-\infty<t<\infty\). La imagen de\(f\) es la superficie\(S\) en\(\mathbb{R}^{3}\) parametrizada por las ecuaciones

\ [\ begin {alineado}
&x=t\ cos (s),\\
&y=t\ sin (s),\\
&z=t.
\ end {alineado}\]

Tenga en cuenta que para un valor fijo de\(t\), la función

\[ \varphi_{1}(s)=(t \cos (s), t \sin (s), t) \nonumber \]

parametriza un círculo de radio\(t\) en el plano\(z=t\) con el centro en\( (0,0,t) \). Por otro lado, para un valor fijo de\(s\), la función

\[ \varphi_{2}(t)=(t \cos (s), t \sin (s), t)=t(\cos (s), \sin (s), 1) \nonumber \]

parametriza una línea a través del origen en la dirección del vector\((\cos (s), \sin (s), 1)\). De ahí que la superficie\(S\) sea un cono en\(\mathbb{R}^{3}\), parte de la cual se muestra en la Figura 4.1.1. Observe cómo se dibujó la superficie trazando las curvas correspondientes a valores fijos de\(s\) y\(t\) (es decir, las curvas parametrizadas por\(\varphi_1\) y\(\varphi_2\)), y luego rellenando los “rectángulos” curvilíneos resultantes.

Figura\(\PageIndex{1}\): Cono parametrizado por\(f(s, t)=(t \cos (s), t \sin (s), t)\)

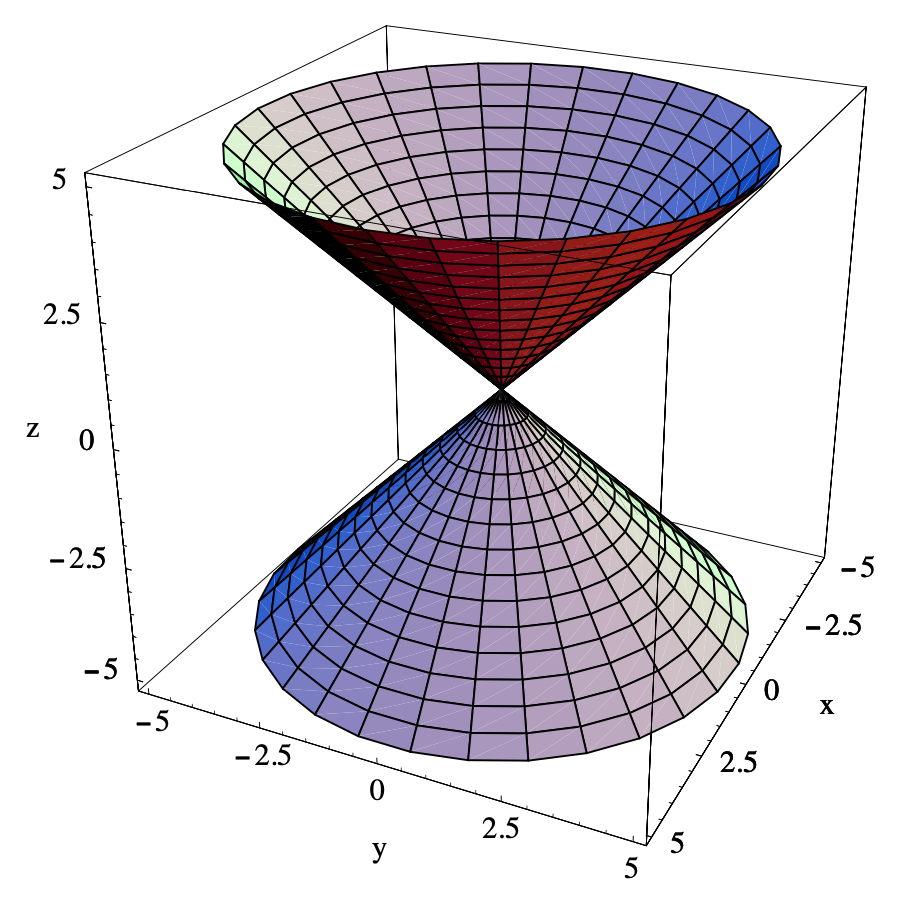
Ejemplo\(\PageIndex{2}\)

Para un fijo\(a>0\), considere la función\(f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{3}\) definida por

\[ f(s, t)=(a \cos (s) \sin (t), a \sin (s) \sin (t), a \cos (t)) \nonumber \]

para\(0 \leq s \leq 2 \pi\) y\(0 \leq t \leq \pi\). La imagen de\(f\) es la superficie\(S\) en\(\mathbb{R}^3\) parametrizada por las ecuaciones

\ [\ begin {align}
&x=a\ cos (s)\ sin (t),\ nonumber\\
&y=a\ sin (s)\ sin (t),\ label {}\\
&z=a\ cos (t). \ nonumber
\ end {align}\]

Tenga en cuenta que estas son las ecuaciones para el cambio de coordenadas esféricas de las variables discutidas en la Sección 3.7, con\(\rho=a, \theta=s\), y\(\varphi = t\). Dado que\(a\) es fijo mientras que\(s\) varía de 0 a\(2 \pi\) y\(t\) varía de 0 a\(\pi\), se deduce que\(S\) es una esfera de radio\(a\) con centro (0, 0 , 0). La Figura 4.1.2 muestra\(S\) cuándo\(a=1\).

Figura\(\PageIndex{2}\): Esfera unitaria parametrizada por\(f(s, t)=(\cos (s) \sin (t), \sin (s) \sin (t), \cos (t))\)

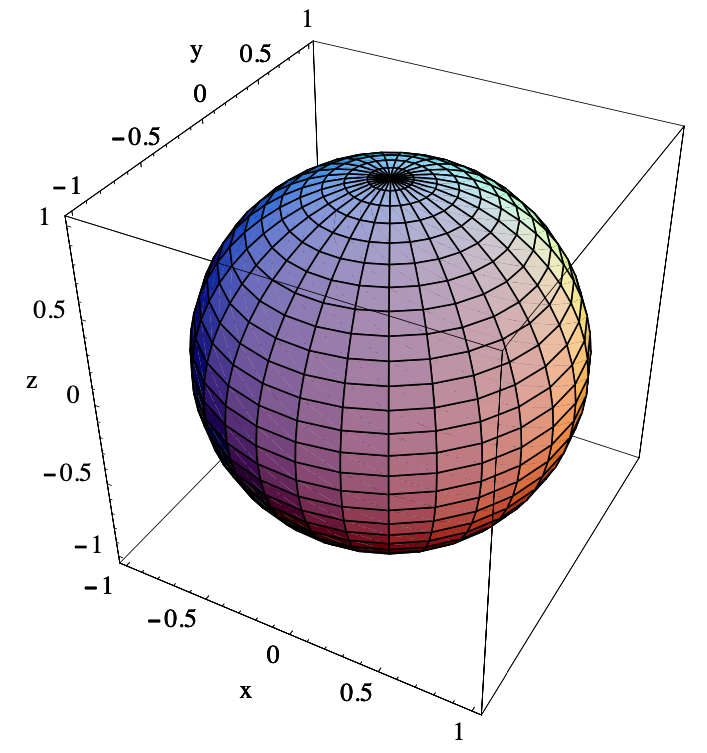
Si no hubiéramos estudiado previamente las coordenadas esféricas, podríamos llegar a esta conclusión de la\(S\) siguiente manera. Primero tenga en cuenta que

\ [\ begin {alineado}
x^ {2} +y^ {2} +z^ {2} &=a^ {2}\ cos ^ {2} (s)\ sin ^ {2} (t) +a^ {2}\ sin ^ {2} (s)\ sin ^ {2} (t) +a^ {2}\ cos ^ {2} (t)\\
&a=^ {2}\ sin ^ {2} (t)\ izquierda (\ cos ^ {2} (s) +\ sin ^ {2} (s)\ derecha) +a^ {2}\ cos ^ {2} (t)\\
&=a^ {2}\ izquierda (\ sin ^ {2} (t) +\ cos ^ {2} (t)\ derecha)\\
&=a^ {2},
\ end {alineado}\]

de donde se deduce que cada punto de\(S\) yace sobre la esfera de radio a centrada en el origen. Ahora por un valor fijo de\(t\),

\[ \varphi_{1}(s)=(a \cos (s) \sin (t), a \sin (s) \sin (t), a \cos (t)) \nonumber \]

parametriza un círculo en el plano\(z=a \cos (t)\) con centro\((0,0, a \cos (t))\) y radio\(a \sin (t)\). Como\(t\) varía de 0 a\(\pi \), estos círculos varían de un círculo en el\(z=a\) plano con centro\( (0,0,a) \) y radio 0 (cuando\(t=0\)) a un círculo en el\(xy\) plano -con centro (0, 0, 0) y radio\(a\) (cuando\(t= \frac{\pi}{2}\)) a un círculo en el\(z=-a\) plano con centro\( (0,0,−a) \) y radio 0 (cuando\(t=\pi\)). En otras palabras, los círculos llenan todas las “líneas de latitud” de la esfera desde el “Polo Norte” hasta el “Polo Sur”, y por lo tanto\(S\) es toda la esfera. También se puede demostrar que las funciones

\[ \varphi_{2}(t)=(a \cos (s) \sin (t), a \sin (s) \sin (t), a \cos (t)) \nonumber \]

parametrizar las “líneas de longitud” de\(S\) como\(s\) varía de 0 a\(2\pi\). Tanto las líneas de “latitud” como de “longitud” son visibles en la Figura 4.2.2.

Ejemplo\(\PageIndex{3}\)

Supongamos\(0<b<a\) y definimos\(f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{3}\) por

\[ f(s, t)=((a+b \cos (t)) \cos (s),(a+b \cos (t)) \sin (s), b \sin (t)) \nonumber \]

para\(0 \leq s \leq 2 \pi\) y\(0 \leq t \leq 2 \pi\). La imagen de\(f\) es la superficie\(T\) parametrizada por las ecuaciones

\ [\ begin {alineado}
&x= (a+b\ cos (t))\ cos (s),\\
&y =( a+b\ cos (t))\ sin (s),\\
&z=b\ sin (t).
\ end {alineado}\]

Tenga en cuenta que para un valor fijo de\(t\),

\[ \varphi_{1}(s)=((a+b \cos (t)) \cos (s),(a+b \cos (t)) \sin (s), b \sin (t)) \nonumber \]

parametriza un círculo en el plano\(z=b \sin (t)\) con centro\((0,0, b \sin (t))\) y radio\(a+b \cos (t)\). En particular, cuando\(t=0\), tenemos un círculo en el\(xy\) plano -con centro (0, 0, 0) y radio\(a+b\); cuando\(t=\frac{\pi}{2}\), tenemos un círculo en el plano\(z=b\) con centro\( (0,0,b) \) y radio\(a\); cuándo\(t=\pi\), tenemos un círculo encendido el\(xy\) -plano con centro (0, 0, 0) y radio\(a-b\); cuando\(t= \frac{3\pi}{2}\), tenemos un círculo en el\(z=-b\) plano con centro\( (0,0,−b) \) y radio\(a\); y cuando\(t=2 \pi \), volvemos a un círculo en el\(xy\) plano -con centro (0 , 0, 0) y radio\(a+b\). Para valores fijos de\(s\), las curvas parametrizadas por

\[ \varphi_{2}(t)=((a+b \cos (t)) \cos (s),(a+b \cos (t)) \sin (s), b \sin (t)) \nonumber \]

no se identifican con facilidad. Sin embargo, algunos casos particulares son esclarecedoras. Cuando\(s=0\), tenemos un círculo en el\(xz\) plano -con centro (\(a\), 0, 0) y radio\(b\); cuando\(s=\frac{\pi}{2}\), tenemos un círculo en el\(yz\) plano -con centro (0,\(a\), 0) y radio\(b\); cuando\(s=\pi\), tenemos un círculo en el\(xz\) plano -con centro (\(-a\), 0, 0) y radio\(b\); cuando\(s=\frac{3\pi}{2}\), tenemos un círculo en el\(yz\) plano -con centro (0 \(-a\), 0) y radio\(b\); y cuando\(t=2\pi\), volvemos a una círculo en el\(xz\) plano -con centro (\(a\), 0, 0) y radio\(b\). Armando todo esto, vemos que\(T\) es un toro, la superficie de un objeto en forma de donut. La figura 4.1.3 muestra uno de esos toro, el caso\(a=3\) y\(b=1\).

Figura\(\PageIndex{3}\): Un toro:\(f(s, t)=((3+\cos (t)) \cos (s),(3+\cos (t)) \sin (s), \sin (t))\)

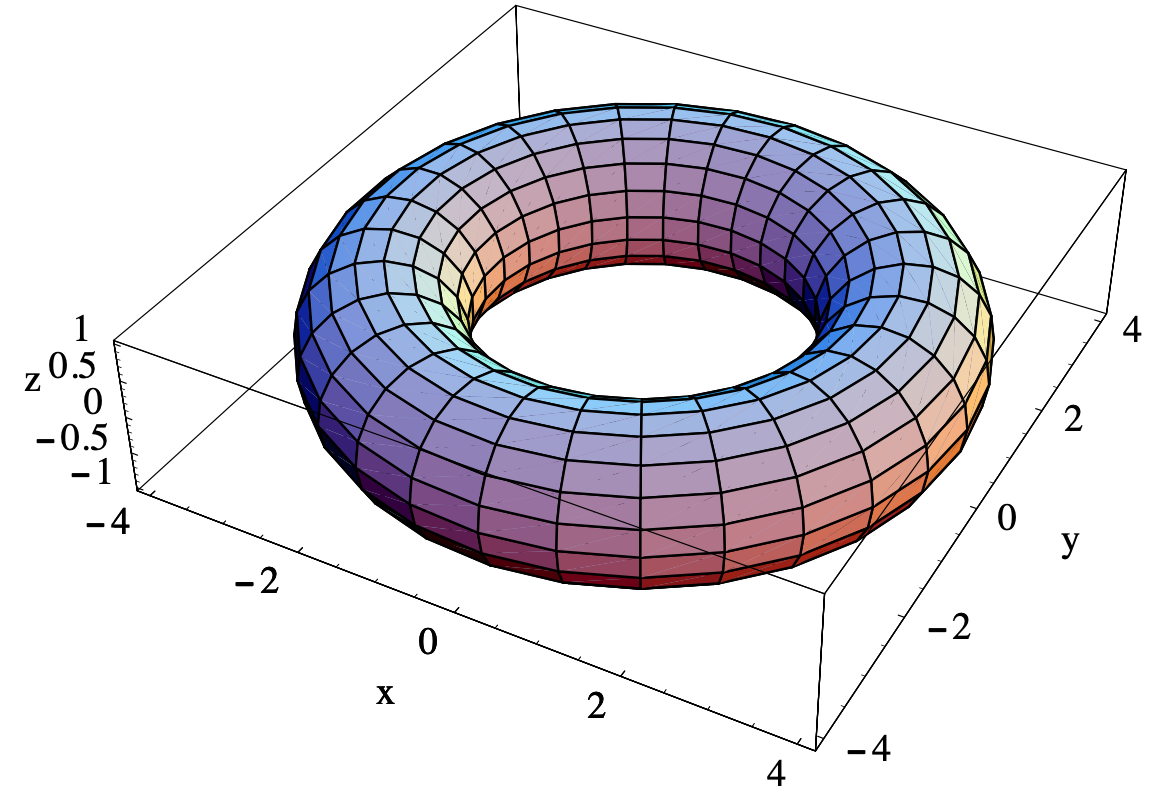
Campos vectoriales

Llamamos a una función\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}\), es decir, una función para la cual el espacio de dominio y rango tienen la misma dimensión, un campo vectorial. Ya hemos visto algunos ejemplos de este tipo de funciones. Por ejemplo, el cambio de funciones variables en la Sección 3.7 fueron de este tipo. También, dada una función\(g: \mathbb{R}^{n} \rightarrow \mathbb{R}\), el gradiente de\(g\),

\[ \nabla g(\mathbf{x})=\left(\frac{\partial}{\partial x_{1}} g(\mathbf{x}), \frac{\partial}{\partial x_{2}} g(\mathbf{x}), \ldots, \frac{\partial}{\partial x_{n}} g(\mathbf{x})\right) , \nonumber \]

es una función de\(\mathbb{R}^n\) a\(\mathbb{R}^n\). Como vimos en nuestra discusión sobre los campos vectoriales de gradiente en la Sección 3.2, una gráfica que muestra los vectores\(f(\mathbf{x})\) en cada punto de una cuadrícula rectangular proporciona una vista geométrica útil de un campo vectorial\(f\).

Ejemplo\(\PageIndex{4}\)

Considere el campo vectorial\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}\) definido por

\[ f(\mathbf{x})=-\frac{\mathbf{x}}{\|\mathbf{x}\|^{2}} \nonumber \]

para todos\(\mathbf{x} \neq \mathbf{0}\). Tenga en cuenta que\(f(\mathbf{x})\) es un vector de longitud

\[ \left\|\frac{\mathbf{x}}{\|\mathbf{x}\|^{2}}\right\|=\frac{\|\mathbf{x}\|}{\|\mathbf{x}\|^{2}}=\frac{1}{\|\mathbf{x}\|} \nonumber \]

apuntando en dirección opuesta a la de\(\mathbf{x}\). Si\(n=2\), las funciones de coordenadas de\(f\) son

\[ f_{1}\left(x_{1}, x_{2}\right)=-\frac{x_{1}}{x_{1}^{2}+x_{2}^{2}} \nonumber \]

y

\[ f_{2}\left(x_{1}, x_{2}\right)=-\frac{x_{2}}{x_{1}^{2}+x_{2}^{2}}. \nonumber \]

La Figura 4.1.4 muestra una gráfica de los vectores\(f(\mathbf{x})\) para este caso, dibujados en una cuadrícula sobre el rectángulo\([-3,3] \times[-3,3]\), y para el caso\(n=3\), usando el cubo\([-3,3] \times[-3,3] \times[-3,3] \). Tenga en cuenta que estas gráficas no muestran los vectores en\(f(\mathbf{x})\) sí, sino vectores que han sido escalados proporcionalmente para que no se superpongan entre sí.

Figura\(\PageIndex{4}\): Campo vectorial\(f(\mathbf{x})=\frac{\mathbf{x}}{\|\mathbf{x}\|^{2}}\) para\(n=2\) y\(n=3\)

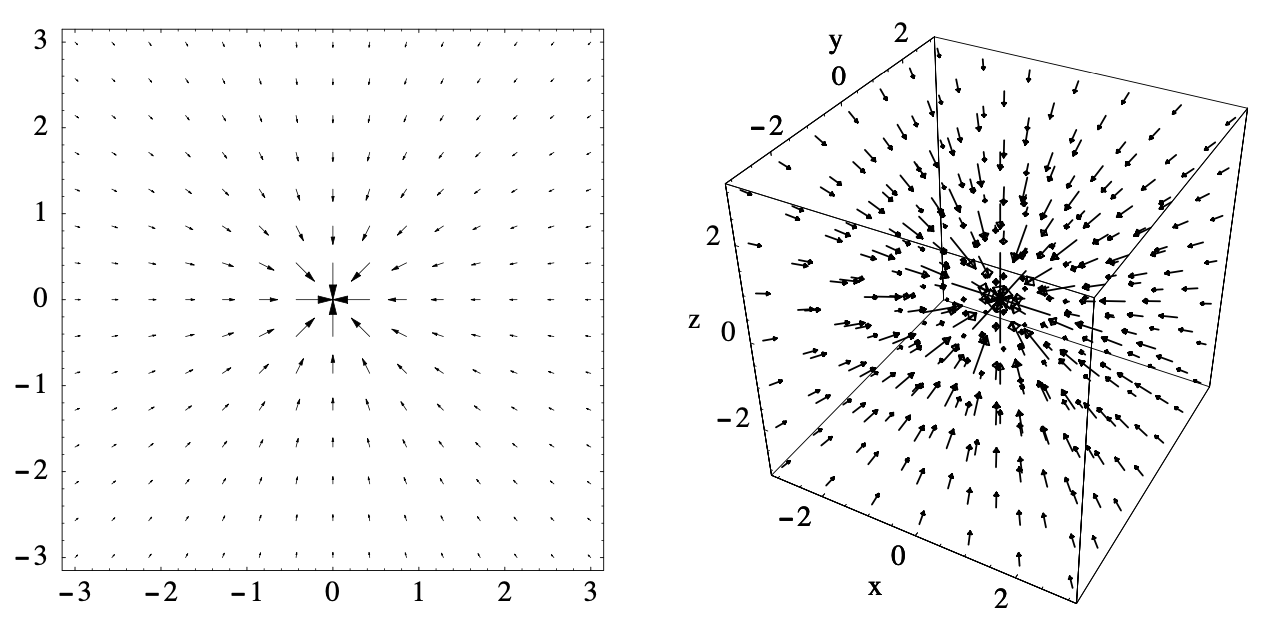
Límites y continuidad

Las definiciones de límites y continuidad para las funciones\(f: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\) siguen el patrón familiar.

Definición\(\PageIndex{1}\)

Dejar\(\mathbf{a}\) ser un punto adentro\(\mathbb{R}^m\) y dejar\(O\) ser el conjunto de todos los puntos en la bola abierta de radio\(r>0\) centrada en\(\mathbf{a}\) excepto\(\mathbf{a}\). Es decir,

\[ O=\left\{\mathbf{x}: \mathbf{x} \in B^{m}(\mathbf{a}, r), \mathbf{x} \neq \mathbf{a}\right\} . \nonumber \]

Supongamos que\(f: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\) se define para todos\(\mathbf{x}\) en\(O\). Decimos que el límite de\(f(\mathbf{x})\) como\(\mathbf{x}\) enfoques\(\mathbf{a}\) es\(\mathbf{L}\), escrito\(\lim _{\mathbf{x} \rightarrow \mathbf{a}} f(\mathbf{x})=\mathbf{L}\), si por cada secuencia de puntos\(\left\{\mathbf{x}_{k}\right\}\) en\(O\),

\[ \lim _{k \rightarrow \infty} f\left(\mathbf{x}_{k}\right)=\mathbf{L} \]

cuando sea\(\lim _{k \rightarrow \infty} \mathbf{x}_{k}=\mathbf{a}\).

En la Sección 2.1 vimos que una secuencia de puntos en\(\mathbb{R}^{n}\) tiene un límite si y sólo si las coordenadas individuales de los puntos en la secuencia tienen cada una un límite. La siguiente proposición es una consecuencia inmediata.

Proposición\(\PageIndex{1}\)

Si\(f_{k}: \mathbb{R}^{m} \rightarrow \mathbb{R}, k=1,2, \ldots, n\), es la función de coordenada\(k\) th de ^{\(f: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\)}, entonces

\[ \lim _{\mathbf{x} \rightarrow \mathbf{a}} f(\mathbf{x})=\left(L_{1}, L_{2}, \ldots, L_{n}\right) \nonumber \]

si y solo si

\[ \lim _{\mathbf{x} \rightarrow \mathbf{a}} f_{k}(\mathbf{x})=L_{k} \nonumber \]

para\(k=1,2, \ldots, n\).

En otras palabras, el cálculo de límites para funciones\(f: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\) reduce al problema familiar de computar límites de funciones de valor real, como se discutió en la Sección 3.1.

Ejemplo\(\PageIndex{5}\)

Si

\[ f(x, y, z)=\left(x^{2}-3 y z, 4 x z\right) , \nonumber \]

una función desde\(\mathbb{R}^3\) hasta\(\mathbb{R}^2\), entonces, por ejemplo,

\[ \lim _{(x, y, z) \rightarrow(1,-2,3)} f(x, y, z)=\left(\lim _{(x, y, z) \rightarrow(1,-2,3)}\left(x^{2}-3 y z\right), \lim _{(x, y, z) \rightarrow(1,-2,3)} 4 x z\right)=(19,12) . \nonumber \]

Definición\(\PageIndex{2}\)

Supongamos que\(f: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\) se define para todos\(\mathbf{x}\) en alguna bola abierta\(B^{n}(\mathbf{a}, r), r>0\). Decimos que\(f\) es continuo en\(\mathbf{a}\) si\(\lim _{\mathbf{x} \rightarrow \mathbf{a}} f(\mathbf{x})=f(\mathbf{a})\).

El siguiente resultado es una consecuencia inmediata de la proposición anterior.

Proposición\(\PageIndex{2}\)

Si\(f_{k}: \mathbb{R}^{m} \rightarrow \mathbb{R}, k=1,2, \ldots, n\), es la función de coordenada\(k\) th de\(f: \mathbb{R}^{m} \rightarrow \mathbb{R}^n\), entonces\(f\) es continuo en un punto\(\mathbf{a}\) si y solo si\(f_k\) es continuo en\(\mathbf{a}\) for\(k=1,2, \ldots, n\).

Es decir, verificar la continuidad de una función\(f: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\) reduce a verificar la continuidad de funciones de valor real, un problema familiar de la Sección 3.1.

Ejemplo\(\PageIndex{6}\)

La función

\[ f(x, y)=\left(3 \sin (x+y), 4 x^{2} y\right) \nonumber \]

tiene funciones de coordenadas

\[ f_{1}(x, y)=3 \sin (x+y) \nonumber \]

y

\[ f_{2}(x, y)=4 x^{2} y . \nonumber \]

Ya que, a partir de nuestros resultados en la Sección 3.1, ambos\(f_1\) y\(f_2\) son continuos en cada punto de\(\mathbb{R}^2\), se deduce que\(f\) es continuo en cada punto de\(\mathbb{R}^2\).

Definición\(\PageIndex{3}\)

Decimos que una función\(f: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\) es continua en un conjunto abierto\(U\) si\(f\) es continua en cada punto\(\mathbf{u}\) de\(U\).

Ejemplo\(\PageIndex{7}\)

Podemos reafirmar la conclusión del ejemplo anterior diciendo que

\[ f(x, y)=\left(3 \sin (x+y), 4 x^{2} y\right) \nonumber \]

es continuo en\(\mathbb{R}^2\).