4.2: Mejores aproximaciones afín

Mejores aproximaciones afín

Las siguientes definiciones deberían parecer muy familiares.

Definición\(\PageIndex{1}\)

Supongamos que\(f: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\) se define sobre una bola abierta que contiene el punto\(\mathbf{c}\). Llamamos a una función afín\(A: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\) la mejor aproximación afín a\(f\) at\(\mathbf{c}\) if (1)\(A(\mathbf{c})=f(\mathbf{c})\) y (2)\(\|R(\mathbf{h})\|\) es\(o(\mathbf{h})\), donde

\[ R(\mathbf{h})=f(\mathbf{c}+\mathbf{h})-A(\mathbf{c}+\mathbf{h}) . \]

Supongamos que\(A: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}\) es la mejor aproximación afín a\(f\) at\(\mathbf{c}\). Entonces, de nuestro trabajo en la Sección 1.5, existe una\(n \times m\) matriz\(M\) y un vector\(\mathbf{b}\) en\(\mathbb{R}^n\) tal que

\[ A(\mathbf{x})=M \mathbf{x}+\mathbf{b} \]

para todos\(\mathbf{x}\) en\(\mathbb{R}^m\). Además, la condición\(A(\mathbf{c})=f(\mathbf{c})\) implica\(f(\mathbf{c})=M \mathbf{c}+\mathbf{b}\), y así\(\mathbf{b}=f(\mathbf{c})-M \mathbf{c}\). De ahí que tengamos

\[ A(\mathbf{x})=M \mathbf{x}+f(\mathbf{c})-M \mathbf{c}=M(\mathbf{x}-\mathbf{c})+f(\mathbf{c}) \label{4.2.3} \]

para todos\(\mathbf{x}\) en\(\mathbb{R}^m\). Así, para encontrar la mejor aproximación afín solo necesitamos identificar la matriz\(M\) en (\(\ref{4.2.3}\)).

Definición\(\PageIndex{2}\)

Supongamos que\(f: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\) se define sobre una bola abierta que contiene el punto\(\mathbf{c}\). Si\(f\) tiene una mejor aproximación afín a\(\mathbf{c}\), entonces decimos que\(f\) es diferenciable en\(\mathbf{c}\). Además, si la mejor aproximación afín a\(f\) at\(\mathbf{c}\) viene dada por

\[ A(\mathbf{x})=M(\mathbf{x}-\mathbf{c})+f(\mathbf{c}) , \]

entonces llamamos a\(M\) la derivada de\(f\) at\(\mathbf{c}\) y escribimos\(D f(\mathbf{c})=M\).

Ahora supongamos\(f: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\) y\(A\) es una función afín con\(A(\mathbf{c})=f(\mathbf{c})\). Let\(f_k\) y\(A_k\) ser las funciones de coordenadas\(k\) th de\(f\) y\(A\), respectivamente, for\(k=1,2, \ldots, n\), y let\(R\) ser la función restante

\ [\ begin {alineado}
R (\ mathbf {h}) &=f (\ mathbf {c} +\ mathbf {h}) -A (\ mathbf {c} +\ mathbf {h})\\
&=\ left (f_ {1} (\ mathbf {c} +\ mathbf {h}) -A_ {1} (\ mathbf {c} +\ mathbf {h}), f_ {2} (\ mathbf {c} +\ mathbf {h}) -A_ {2} (\ mathbf {c} +\ mathbf {h}),\ ldots, f_ {n} (\ mathbf {c} +\ mathbf {h}) -A_ {n} (\ mathbf {c} +\ mathbf { h})\ derecha).
\ end {alineado}\]

Entonces

\[ \frac{R(\mathbf{h})}{\|\mathbf{h}\|}=\left(\frac{f_{1}(\mathbf{c}+\mathbf{h})-A_{1}(\mathbf{c}+\mathbf{h})}{\|\mathbf{h}\|}, \frac{f_{2}(\mathbf{c}+\mathbf{h})-A_{2}(\mathbf{c}+\mathbf{h})}{\|\mathbf{h}\|}, \ldots, \frac{f_{n}(\mathbf{c}+\mathbf{h})-A_{n}(\mathbf{c}+\mathbf{h})}{\|\mathbf{h}\|}\right) , \nonumber \]

y así

\[ \lim _{\mathbf{h} \rightarrow \mathbf{0}} \frac{\| R(\mathbf{h} \|}{\|\mathbf{h}\|}=0 , \]

es decir,\(A\) es la mejor aproximación afín a\(f\) at\(\mathbf{c}\), si y solo si

\[ \lim _{\mathbf{h} \rightarrow \mathbf{0}} \frac{f_{k}(\mathbf{c}+\mathbf{h})-A_{k}(\mathbf{c}+\mathbf{h})}{\|\mathbf{h}\|}=0 \label{4.2.6} \]

para\(k=1,2, \ldots, n\). Pero (\(\ref{4.2.6}\)) es la afirmación que\(A_k\) es la mejor aproximación afín a\(f_k\) at\(\mathbf{c}\). En otras palabras,\(A\) es la mejor aproximación afín a\(f\) at\(\mathbf{c}\) if y solo si\(A_k\) es la mejor aproximación afín a\(f_k\) at\(\mathbf{c}\) for \(k=1,2, \ldots, n\). Este resultado tiene muchas consecuencias interesantes.

Proposición\(\PageIndex{1}\)

Si\(f_{k}: \mathbb{R}^{m} \rightarrow \mathbb{R}\) es la función de coordenada\(k\) th de\(f: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\), entonces\(f\) es diferenciable en un punto\(\mathbf{c}\) si y solo si\(f_k\) es diferenciable en\(\mathbf{c}\) for\(k=1,2, \ldots, n\).

Definición\(\PageIndex{3}\)

Si\(f_{k}: \mathbb{R}^{m} \rightarrow \mathbb{R}\) es la función de coordenada\(k\) th de\(f: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\), entonces decimos que\(f\) está\(C^1\) en un conjunto abierto\(U\) si\(f_k\) está\(C^1\) encendido\(U\) para\(k=1,2, \ldots, n\).

Al poner nuestros resultados en la Sección 3.3 junto con la proposición y definición anteriores, tenemos el siguiente resultado básico.

Teorema\(\PageIndex{1}\)

Si\(f: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\) está\(C^1\) en una bola abierta que contiene el punto\(\mathbf{c}\), entonces\(f\) es diferenciable en\(\mathbf{c}\).

Supongamos que\(f: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\) es diferenciable en\(\mathbf{c}=\left(c_{1}, c_{2}, \ldots, c_{m}\right)\) con la mejor aproximación afín\(A\) \(f_{k}: \mathbb{R}^{m} \rightarrow \mathbb{R}\)y y\(A_{k}: \mathbb{R}^{m} \rightarrow \mathbb{R}\) son las funciones coordinadas de\(f\) y\(A\), respectivamente, para\(k=1,2, \ldots, n\). Dado que\(A_k\) es la mejor aproximación afín a\(f_k\) at\(\mathbf{c}\), sabemos por la Sección 3.3 que

\[ A_{k}(\mathbf{x})=\nabla f_{k}(\mathbf{c}) \cdot(\mathbf{x}-\mathbf{c})+f_{k}(\mathbf{c}) \]

para todos\(\mathbf{x}\) en\(\mathbb{R}^m\). De ahí que al escribir los vectores como vectores de columna, tenemos

\ [\ begin {align}
A (\ mathbf {x}) =&\ left [\ begin {array} {c}
A_ {1} (\ mathbf {x})\\
A_ {2} (\ mathbf {x})\\
\ vdots\\
A_ {n} (\ mathbf {x})
\ end {array}\ derecha]\ nonumber\\
=&\ izquierda [\ begin {array} {cccc}
\ nabla f_ {1} (\ mathbf {c})\ cdot (\ mathbf {x} -\ mathbf {c}) +f_ {1} (\ mathbf {c})\
\ nabla f_ {2} (\ mathbf {c})\ cdot (\ mathbf {x} -\ mathbf {c}) +f_ {2} (\ mathbf {c})\\
\ vdots\
\ nabla f_ {n} (\ mathbf {c})\ cdot (\ mathbf {x} -\ mathbf {c}) +f_ {n} (\ mathbf {c})
\ end {array}\ derecha]\ nonumber\\
=&\ izquierda [\ begin {array} {cccc}
\ frac {\ parcial} {\ parcial} {\ parcial x_ {1}} f_ {1} (\ mathbf {c}) &\ frac {\ parcial} {\ parcial x_ {2}} f_ {1} (\ mathbf {c}) &\ cdots &\ frac {\ parcial} x_ {m}} f_ {1} (\ mathbf {c})\
\ frac {\ parcial} {\ parcial x_ {1}} f_ {2} (\ mathbf {c}) &\ frac {\ parcial} {\ parcial x_ {2}} f_ {2} (\ mathbf {c}) &\ cdots &\ frac {\ parcial} {x_ {m}} f_ {2} (\ mathbf {c})\\ vdots &
\ vdots &\ ddots &\ vdots\\ vdots\
\ frac {\ parcial} {parcial x_ {1}} f_ {n} (\ mathbf {c}) &\ frac {\ parcial} {\ parcial} {\ parcial x_ {2}} f_ {n} (\ mathbf {c}) & amp;\ cdots &\ frac {\ parcial} {x_ {m}} f_ {n} (\ mathbf {c})
\ end {array}\ derecha]\ izquierda [\ begin {array} {c}
x_ {1} -c_ {1}\
x_ {2} -c_ {2} -c_ {2}
\\ vdots\\
x_ {m} -c_ {m}
\ fin array}\ derecha] +\ left [\ begin {array} {c}
f_ {1} (\ mathbf {c})\\
f_ {2} (\ mathbf {c})\\
\ vdots\\
f_ {m} (\ mathbf {c})
\ end {array}\ right]. \ label {4.2.8}
\ end {align}\]

De ello se deduce que la\(n \times m \) matriz in (\(\ref{4.2.8}\)) es la derivada de\(f\).

Teorema\(\PageIndex{2}\)

Si\(f: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\) es diferenciable en un punto\(\mathbf{c}\), entonces la derivada de\(f\) at\(\mathbf{c}\) viene dada por

\ [D f (\ mathbf {c}) =\ left [\ begin {array} {cccc}
\ frac {\ parcial} {\ parcial} {\ parcial x_ {1}} f_ {1} (\ mathbf {c}) &\ frac {\ parcial} {\ parcial} {2}} f_ {1} (\ mathbf {c}) &\ cdots &\ frac\ parcial} {x_ {m}} f_ {1} (\ mathbf {c})\
\ frac {\ parcial} {\ parcial x_ {1}} f_ {2} (\ mathbf {c}) &\ frac {\ parcial } {\ parcial x_ {2}} f_ {2} (\ mathbf {c}) &\ cdots &\ frac {\ parcial} {x_ {m}} f_ {2} (\ mathbf {c})\\
\ vdots &\ vdots &\ ddots &\ vdots\\ vdots
\\ frac {\ parcial} {\ parcial} {1}} f_ {n} (\ mathbf {c}) &\ frac {\ parcial} {\ parcial x_ {2}} f_ {n} (\ mathbf {c}) &\ cdots &\ frac {\ parcial} {x_ {m}} f_ {n} (\ mathbf {c})
\ end {array}\ right]. \ label {4.2.9}\]

Llamamos a la matriz en (\(\ref{4.2.9}\)) la matriz jacobiana de\(f\), según el matemático alemán Carl Gustav Jacob Jacobi (1804-1851). Obsérvese que hemos visto antes esta matriz en nuestra discusión del cambio de variables en integrales en la Sección 3.7.

Ejemplo\(\PageIndex{1}\)

Considere la función\(f: \mathbb{R}^{3} \rightarrow \mathbb{R}^{2}\) definida por

\[ f(x, y, z)=(x y z, 3 x-2 y z) . \nonumber \]

Las funciones coordinadas de\(f\) son

\[ f_{1}(x, y, z)=x y z \nonumber \]

y

\[ f_{2}(x, y, z)=3 x-2 y z \text {. } \nonumber \]

Ahora

\[ \nabla f_{1}(x, y, z)=(y z, x z, x y) \nonumber \]

y

\[ \nabla f_{2}(x, y, z)=(3,-2 z,-2 y) , \nonumber \]

así que el jacobiano de\(f\) es

\ [D f (x, y, z) =\ left [\ begin {array} {ccc}
y z & x z & x y\\
3 & -2 z & -2 y
\ end {array}\ right]. \ nonumber\]

De ahí que, por ejemplo,

\ [D f (1,2, -1) =\ left [\ begin {array} {rrr}
-2 & -1 & 2\\
3 & 2 & -4
\ end {array}\ right]. \ nonumber\]

Ya que\(f(1,2,-1)=(-2,7)\), la mejor aproximación afín a\(f\) at (1, 2, −1) es

\ [\ begin {aligned}
A (x, y, z) &=\ left [\ begin {array} {rrr}
-2 & -1 & 2\\
3 & 2 & -4
\ end {array}\ right]\ left [\ begin {array} {l}
x-1\
y-2\
z+1
\ end {array}\ right] +\ left [\ begin { array} {r}
-2\\
7
\ end {array}\ derecha]\\
&=\ izquierda [\ begin {array} {c}
-2 (x-1) - (y-2) +2 (z+1) -2\\
3 (x-1) +2 (y-2) -4 (z+1) +7
\ end {array}\ derecha]\\
&=\ left [\ begin {array} {c}
-2 x-y+2 z+4\\
3 x+2 y-4 z-4
\ end {array}\ right].
\ end {alineado}\]

Planos tangentes

Supongamos que\(f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{3}\) parametriza una superficie\(S\) en\(\mathbb{R}^3\). Si\(f_1\),\(f_2\), y\(f_3\) son las funciones de coordenadas de\(f\), entonces la mejor aproximación afín a\(f\) en un punto\((s_0,t_0)\) viene dada por

\ [\ begin {align}
&A (s, t) =\ izquierda [\ begin {array} {ll}
\ frac {\ parcial} {\ parcial} f_ {1}\ izquierda (t_ {0}, s_ {0}\ derecha) &\ frac {\ parcial} {\ parcial} {\ t parcial} f_ {1}\ izquierda (t_ {0}, s_ {0}\ derecha)\
\\ frac {\ parcial} {\ parcial s} f_ {2}\ izquierda (t_ {0}, s_ {0}\ derecha) &\ frac {\ parcial} {\ parcial t} f_ {2}\ izquierda (t_ {0}, s_ {0}\ derecha)\
\ frac {\ parcial} {\ parcial} f_ {3}\ izquierda (t_ {0}, s_ {0}\ derecha) &\ frac {\ parcial} {\ parcial} {\ t parcial} f_ {3}\ izquierda (t_ {0}, s_ {0} derecha)
\ end {array}\ derecha]\ left [\ begin {array} {c}
s-s_ {0}\
t-t_ {0}
\ end {array }\ derecha] +\ izquierda [\ begin {array} {l}
f_ {1}\ izquierda (s_ {0}, t_ {0}\ derecha)\\
f_ {2}\ izquierda (s_ {0}, t_ {0}\ derecha)\
f_ {3}\ izquierda (s_ {0}, t_ {0}\ derecha)
\ end {array}\ derecha]\ nonumber\\
&=\ left [\ begin {array} {l}
\ frac {\ parcial} {\ parcial s} f_ {1}\ izquierda (s_ {0}, t_ {0}\ derecha)\
\ frac {\ parcial} {\ parcial} f_ {2}\ izquierda (s_ {0}, t_ {0}\ derecha)\\ frac {
\ parcial} {\ parcial} {\ s} f_ {3}\ izquierda (s_ {0}, t_ {0}\ derecha)
\ end {array}\ derecha]\ izquierda (s-s_ {0}\ derecha) +\ izquierda [\ begin {array} {l}
\ frac {\ parcial} {\ t parcial} f_ {1} \ izquierda (s_ {0}, t_ {0}\ derecha)\
\ frac {\ parcial} {\ parcial} f_ {2}\ izquierda (s_ {0}, t_ {0}\ derecha)\\ frac {
\ parcial} {\ parcial} {\ t parcial} f_ {3}\ izquierda (s_ {0}, t_ {0}\ derecha)
\ end {array}\ derecha]\ izquierda (t-t_ {0}\ derecha) +\ izquierda [\ begin {array} {l}
f_ {1}\ izquierda (s_ {0}, t_ {0}\ derecha)\\
f_ {2}\ izquierda (s_ {0}, t_ {0}\ derecha)\\
f_ {3}\ izquierda (s_ {0}, t_ {0}\ derecha)
\ end {array}\ derecha]\ label {4.2.10}
\ end {align}\]

Si los vectores

\ [\ mathbf {v} =\ izquierda [\ begin {array} {l}
\ frac {\ parcial} {\ parcial} f_ {1}\ izquierda (s_ {0}, t_ {0}\ derecha)\
\ frac {\ parcial} {\ parcial} {\ parcial} f_ {2}\ izquierda (s_ {0}, t_ {0}\ derecha)\
\ frac {\ parcial} {\ parcial s} f_ {3}\ izquierda (s_ {0}, t_ {0}\ derecha)
\ end {array}\ derecha]\ label {4.2.11} \]

y

\ [\ mathbf {w} =\ izquierda [\ begin {array} {l}
\ frac {\ parcial} {\ parcial} f_ {1}\ izquierda (s_ {0}, t_ {0}\ derecha)\\ frac {
\ parcial} {\ parcial} {\ t parcial} f_ {2}\ izquierda (s_ {0}, t_ {0}\ derecha)\
\ frac {\ parcial} {\ t parcial} f_ {3}\ izquierda (s_ {0}, t_ {0}\ derecha)
\ end {array}\ derecha]\ label {4.2.12} \]

son linealmente independientes, entonces (\(\ref{4.2.10}\)) implica que la imagen de\(A\) es un plano en el\(\mathbb{R}^3\) que pasa por el punto\(f\left(s_{0}, t_{0}\right)\) en la superficie\(S\). Además, si dejamos\(C_1\) ser la curva\(S\) a través del punto\(f\left(s_{0}, t_{0}\right)\) parametrizado por\(\varphi_{1}(s)=f\left(s, t_{0}\right)\) y\(C_2\) ser la curva\(S\) a través del punto\(f\left(s_{0}, t_{0}\right)\) parametrizado por\(\varphi_{2}(t)=f\left(s_{0}, t\right)\), entonces\(\mathbf{v}\) es tangente a\(C_1\) at\(f\left(s_{0}, t_{0}\right)\) y\(\mathbf{w}\) es tangente a\(C_2\) at\(f\left(s_{0}, t_{0}\right)\). De ahí que llamemos a\(A\) la imagen del plano tangente a la superficie\(S\) en el punto\(f\left(s_{0}, t_{0}\right)\).

Ejemplo\(\PageIndex{2}\)

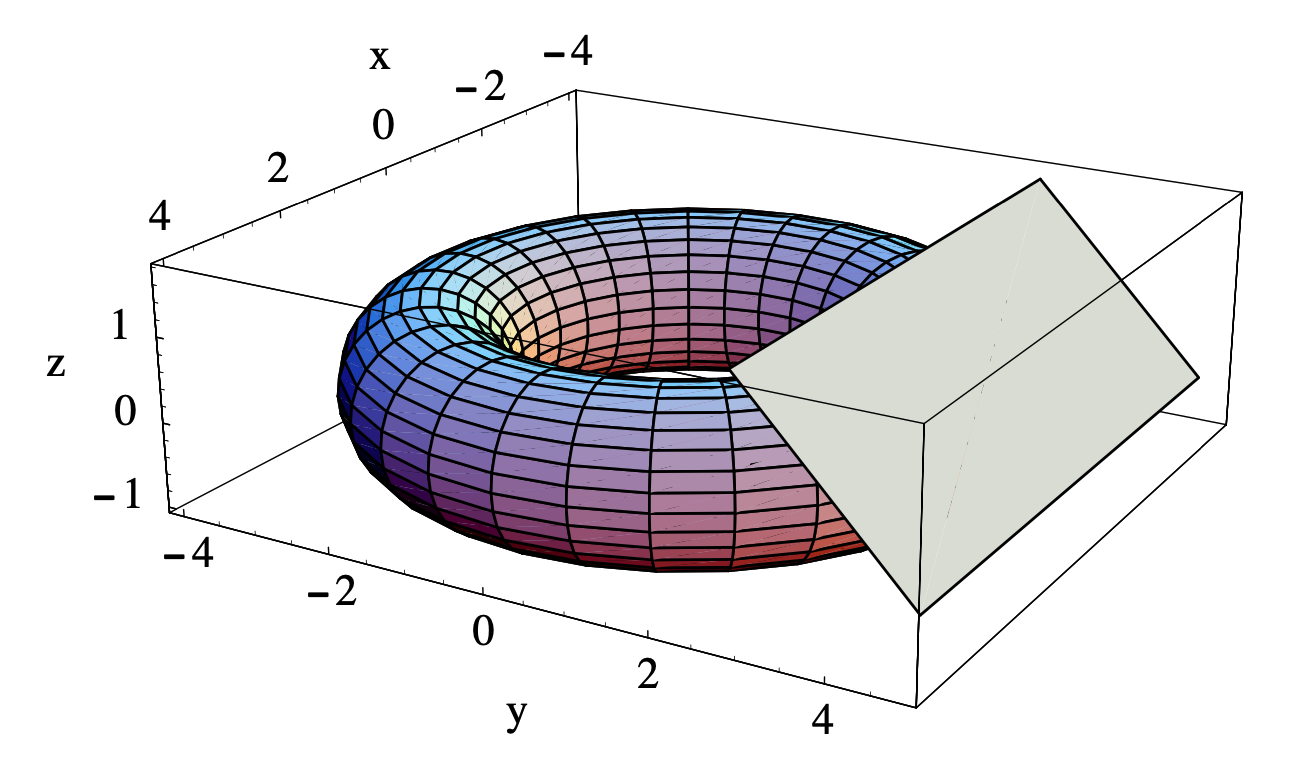
Deja\(T\) ser el toro parametrizado por

\[ f(s, t)=((3+\cos (t)) \cos (s),(3+\cos (t)) \sin (s), \sin (t)) \nonumber \]

para\(0 \leq s \leq 2 \pi\) y\(0 \leq t \leq 2 \pi\). Entonces

\ [D f (s, t) =\ left [\ begin {array} {cc}
- (3+\ cos (t))\ sin (s) & -\ sin (t)\ cos (s)\\
(3+\ cos (t))\ cos (s) & -\ sin (t)\ sin (s)\\
0 &\ cos (t)
\ end {array}\ derecho]. \ nonumber\]

Así, por ejemplo,

\ [\ nombreoperador {Df}\ izquierda (\ frac {\ pi} {2},\ frac {\ pi} {4}\ derecha) =\ left [\ begin {array} {cc}
-\ left (3+\ frac {1} {\ sqrt {2}}\ derecha) & 0\\
0 & -\ frac {1} {\ sqrt {2}}\
0 &\ frac {1} {\ sqrt {2}}
\ end {array}\ right]. \ nonumber\]

Desde

\[ f\left(\frac{\pi}{2}, \frac{\pi}{4}\right)=\left(0,3+\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right) \text {, } \nonumber \]

la mejor aproximación afín a\(f\) at\(\left(\frac{\pi}{2}, \frac{\pi}{4}\right)\) es

\ [A (s, t) =\ left [\ begin {array} {cc}
-\ left (3+\ frac {1} {\ sqrt {2}}\ right) & 0\\
0 & -\ frac {1} {\ sqrt {2}}\\
0 &\ frac {1} {\ sqrt {2}}
\ end {array}\ derecha]\ izquierda [comenzar\ {array} {c}
s-\ frac {\ pi} {2}\\
t-\ frac {\ pi} {4}
\ end {array}\ right] +\ left [\ begin {array} {c}
0\\
3+\ frac {1} {\ sqrt {2}}\\
\ frac {1} {\ sqrt {2}}
\ end {array}\ derecha]\ nonumber\]

\ [=\ left [\ begin {array} {c}
-\ left (3+\ frac {1} {\ sqrt {2}}\ right)\\

0
\ end {array}\ right]\ left (s-\ frac {\ pi} {2}\ right) +\ left [\ begin {array} {c}
0\
-\ frac {1} {\ sqrt {2}}\
\ frac {1} {\ sqrt {2}}
\ end { array}\ derecha]\ izquierda (t-\ frac {\ pi} {4}\ derecha) +\ izquierda [\ begin {array} {c}
0\\
3+\ frac {1} {\ sqrt {2}}\
\ frac {1} {\ sqrt {2}}
\ end {array}\ derecha]. \ nonumber\]

De ahí

\ [\ begin {alineado}
&x=-\ izquierda (3+\ frac {1} {\ sqrt {2}}\ derecha)\ izquierda (s-\ frac {\ pi} {2}\ derecha),\\
&y=-\ frac {1} {\ sqrt {2}}\ izquierda (t-\ frac {\ pi} {4}\ derecha) +3+\ frac {1} {\ sqrt {2}},\\
&z=\ frac {1} {\ sqrt {2}}\ left (t-\ frac {\ pi} {4}\ derecha) +\ frac {1} {\ sqrt {2}},
\ end { alineado}\]

son ecuaciones paramétricas para el plano\(P\) tangente a\(T\) at\(\left(0,3+\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)\). Ver Figura 4.2.1.

Figura\(\PageIndex{1}\): Torus con plano tangente

Regla de la cadena

Ahora estamos en condiciones de afirmar la regla de la cadena en su forma más general. Considerar funciones\(g: \mathbb{R}^{m} \rightarrow \mathbb{R}^{q}\) y\(f: \mathbb{R}^{q} \rightarrow \mathbb{R}^{n}\) y supongamos\(g\) es diferenciable en\(\mathbf{c}\) y\(f\) es diferenciable en\(g(\mathbf{c})\). Dejar\(h: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\) ser la composición\(h(\mathbf{x})=f(g(\mathbf{x}))\) y denotar las funciones coordinadas de\(f\)\(g\),, y\(h\) por\(f_{i}, i=1,2, \ldots, n, g_{j}, j=1,2 \ldots, q\), y\(h_{k}, k=1,2, \ldots, n\), respectivamente. Entonces, para\(k=1,2, \ldots, n\),

\[ h_{k}\left(x_{1}, x_{2}, \ldots, x_{m}\right)=f_{k}\left(g_{1}\left(x_{1}, x_{2}, \ldots, x_{m}\right), g_{2}\left(x_{1}, x_{2}, \ldots, x_{m}\right), \ldots, g_{q}\left(x_{1}, x_{2}, \ldots, x_{m}\right)\right) . \nonumber \]

Ahora bien, si arreglamos\(m-1\) de las variables\(x_{1}, x_{2}, \ldots, x_{m}\), digamos\(x_j\), todas menos, entonces\(h_k\) es la composición de una función de\(\mathbb{R}\) a\(\mathbb{R}^q\) con una función de\(\mathbb{R}^q\) a\(\mathbb{R}\). Por lo tanto, podemos usar la regla de la cadena de la Sección 3.3 para calcular\(\frac{\partial}{\partial x_{j}} h_{k}(\mathbf{c})\), es decir,

\ [\ comenzar {reunir}
\ frac {\ parcial} {\ parcial x_ {j}} h_ {k} (\ mathbf {c}) =\ nabla f_ {k} (g (\ mathbf {c}))\ cdot\ izquierda (\ frac {\ parcial} {\ parcial} {j}} g_ {1} (\ mathbf {c}),\ frac {\ parcial} {j} g_ {1} (\ mathbf {c}),\ frac {\ parcial} {j} ac {\ parcial} {\ parcial x_ {j}} g_ {2} (\ mathbf {c}),\ ldots,\ frac {\ parcial} {x_ {j}} g_ {q} (\ mathbf {c})\ derecha)\ nonumber\\
=\ frac {\ parcial} {\ parcial x_ {1}} f_ {k} (g (\ mathbf {c}))\ frac {\ parcial} {\ parcial} {j}} g_ {1} (\ mathbf {c}) +\ frac {\ parcial} {\ parcial} {\ parcial x_ {2}} f_ {k} (g (\ mathbf {c}))\ frac {\ parcial} {\ parcial x_ {j}} g_ {2} (\ mathbf {c}) +\ label {4.2.13}\\
\ cdots+\ frac {\ parcial} {\ parcial} {q}} f_ {k} (g (\ mathbf {c}))\ frac {\ parcial} {\ parcial} {\ parcial x_ {j}} g_ {q} (\ mathbf {c}). \ nonumber
\ fin {reunir}\]

De ahí que\(\frac{\partial}{\partial x_{j}} h_{k}(\mathbf{c})\) sea igual al producto punto de la fila\(k\) th de\(D f(g(\mathbf{c}))\) con la\(j\) ésima columna de\(D g(\mathbf{c})\). Además, si\(g\) está\(C^1\) en una bola abierta alrededor\(\mathbf{c}\) y\(f\) está\(C^1\) sobre una bola abierta alrededor\(g(\mathbf{c})\), entonces (\(\ref{4.2.13}\)) muestra que\(\frac{\partial}{\partial x_{j}} h_{k}\) es continuo sobre una bola abierta alrededor\(\mathbf{c}\). De nuestros resultados en la Sección 3.3 se desprende que\(h\) es diferenciable en\(\mathbf{c}\). Ya que\(\frac{\partial}{\partial x_{j}} h_{k}\) es la entrada en la fila\(k\) th y\(j\) th columna de\(\operatorname{Dh}(\mathbf{c})\), (\(\ref{4.2.13}\)) implica\(\operatorname{Dh}(\mathbf{c})=D f(g(\mathbf{c})) D g(\mathbf{c})\). Este resultado, la regla de la cadena, puede probarse sin asumir que\(f\) y\(g\) son ambos\(C^1\), y así señalamos el resultado más general en el siguiente teorema.

Teorema: Regla de la Cadena\(\PageIndex{3}\)

Si\(g: \mathbb{R}^{m} \rightarrow \mathbb{R}^{q}\) es diferenciable en\(\mathbf{c}\) y\(f: \mathbb{R}^{q} \rightarrow \mathbb{R}^{n}\) es diferenciable en\(g(\mathbf{c})\), entonces\(f \circ g\) es diferenciable en\(\mathbf{c}\) y

\[ D(f \circ g)(\mathbf{c})=D f(g(\mathbf{c})) D g(\mathbf{c}) . \]

Equivalentemente, la regla de la cadena dice que si\(A\) es la mejor aproximación afín a\(g\) at\(\mathbf{c}\) y\(B\) es la mejor aproximación afín a\(f\) at\(g(\mathbf{c})\), entonces\(B \circ A\) es la mejor aproximación afín a\(f \circ g\) at\(\mathbf{c}\). Es decir, la mejor aproximación afín a una composición de funciones es la composición de las mejores aproximaciones afinas individuales.

Ejemplo\(\PageIndex{3}\)

Supongamos que\(g: \mathbb{R}^{2} \rightarrow \mathbb{R}^{3}\) está definido por

\[ g(s, t)=(\cos (s) \sin (t), \sin (s) \sin (t), \cos (t)) \nonumber \]

y\(f: \mathbb{R}^{3} \rightarrow \mathbb{R}^{2}\) se define por

\[ f(x, y, z)=\left(10 x y z, x^{2}-y z\right) . \nonumber \]

Entonces

\ [D g (s, t) =\ left [\ begin {array} {cc}
-\ sin (s)\ sin (t) &\ cos (s)\ cos (t)\ cos (t)
\\ cos (s)\ sin (t) &\ sin (s)\ cos (t)\
0 & -\ sin (t)
\ end {array}\ derecha]\ nonumber\]

y

\ [D f (x, y, z) =\ left [\ begin {array} {ccc}
10 y z y 10 x z y 10 x y\\
2 x & -z & -y
\ end {array}\ right]. \ nonumber\]

Vamos\(h(s, t)=f(g(s, t))\). Para encontrar\(D h\left(\frac{\pi}{4}, \frac{\pi}{4}\right)\), primero notamos que

\[ g\left(\frac{\pi}{4}, \frac{\pi}{4}\right)=\left(\frac{1}{2}, \frac{1}{2}, \frac{1}{\sqrt{2}}\right) , \nonumber \]

\ [D g\ izquierda (\ frac {\ pi} {4},\ frac {\ pi} {4}\ derecha) =\ izquierda [\ begin {array} {rr}
-\ frac {1} {2} &\ frac {1} {2}\
\ frac {1} {2} &\ frac {1} {2}\\
0 & -\ frac {1}} {\ sqrt {2}}
\ end {array}\ derecha]\ nonumber\]

y

\ [D f\ izquierda (g\ izquierda (\ frac {\ pi} {4},\ frac {\ pi} {4}\ derecha)\ derecha) =D f\ izquierda (\ frac {1} {2},\ frac {1} {2},\ frac {1} {\ sqrt {2}}\ derecha) =\ izquierda [\ begin {array} {ccc}
\ frac {5} {\ sqrt {2}} &\ frac {5} {\ sqrt {2}} &\ frac {5} {2}\\
1 & -\ frac {1} {\ sqrt {2}} & -\ frac {1} {2}
\ end { array}\ derecho]. \ nonumber\]

Por lo tanto

\ [\ begin {alineado}
\ nombreoperador {Dh}\ izquierda (\ frac {\ pi} {4},\ frac {\ pi} {4}\ derecha) &=D f\ izquierda (g\ izquierda (\ frac {\ pi} {4},\ frac {\ pi} {4}\ derecha)\ derecha) D g\ izquierda (\ frac {\ pi} {4},\ frac {\ pi} {4}\ derecha)\\
&=\ izquierda [\ begin {array} {ccc}
\ frac {5} {\ sqrt {2}} &\ frac {5} {\ sqrt {2}} & amp;\ frac {5} {2}\\
1 & -\ frac {1} {\ sqrt {2}} & -\ frac {1} {2}
\ end {array}\ right]\ left [\ begin {array} {rr}
-\ frac {1} {2} &\ frac {1} {2} {2}
\ frac {1} {2} &\ frac {1} {2}\\
0 & -\ frac {1} {\ sqrt {2}}
\ end {array}\ derecha]\ \
&=\ left [\ begin {array} {cc}
0 &\ frac {5} {2\ sqrt {2}}\\
-\ frac {1+\ sqrt {2}} {2\ sqrt {2}} &\ frac {1} {2}
\ end {array}\ right].
\ end {alineado}\]