4.3: Integrales de línea

Motivaremos el concepto matemático de una línea integral a través de una discusión inicial del concepto físico de trabajo.

Trabajo

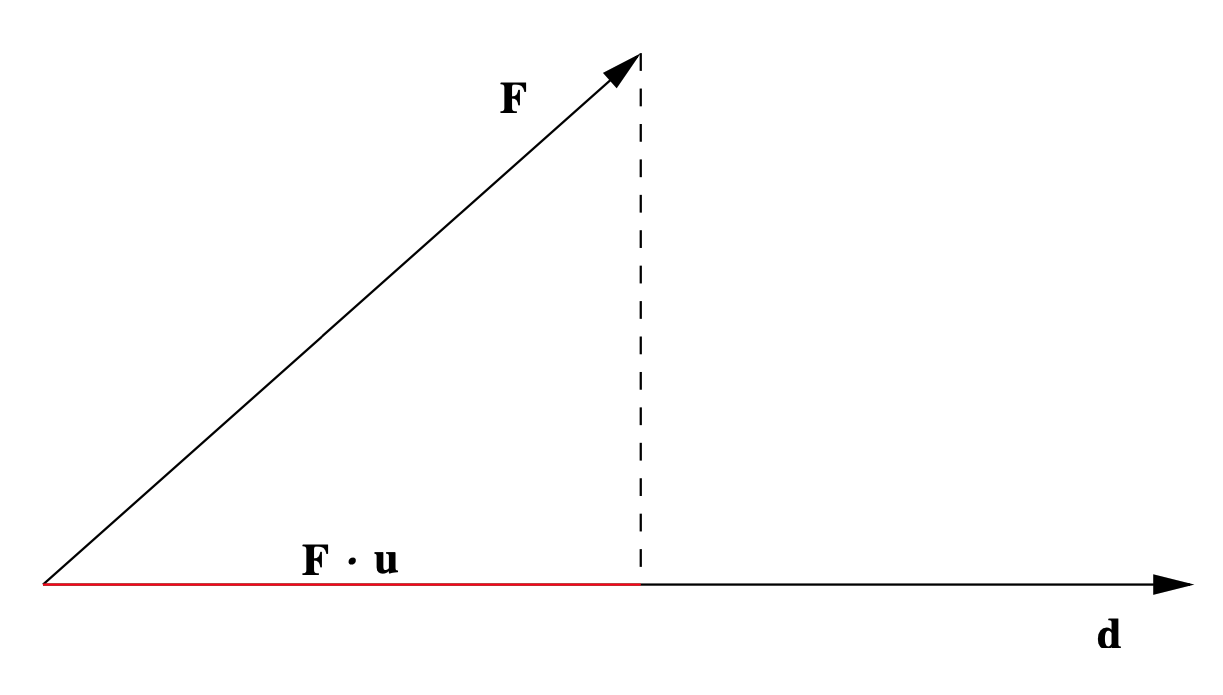
Si una fuerza de magnitud constante\(F\) está actuando en la dirección del movimiento de un objeto a lo largo de una línea, y el objeto se mueve una distancia\(d\) a lo largo de esta línea, entonces llamamos a\(Fd\) la cantidad el trabajo realizado por la fuerza sobre el objeto. Más generalmente, si el vector\(\mathbf{F}\) representa una fuerza constante que actúa sobre un objeto a medida que se mueve a lo largo de un vector de desplazamiento\(\mathbf{d}\), entonces

\[ \mathbf{F} \cdot \frac{\mathbf{d}}{\|\mathbf{d}\|} \label{4.3.1} \]

es la magnitud de\(\mathbf{F}\) en la dirección del movimiento (ver Figura 4.3.1) y definimos

\[ \left(\mathbf{F} \cdot \frac{\mathbf{d}}{\|\mathbf{d}\|}\right)\|\mathbf{d}\|=\mathbf{F} \cdot \mathbf{d} \label{4.3.2} \]

ser el trabajo realizado por\(\mathbf{F}\) sobre el objeto cuando es desplazado por\(\mathbf{d}\).

Figura\(\PageIndex{1}\): Magnitud de\(\mathbf{F}\) en la dirección de\(\mathbf{d}\) es\(\mathbf{F} \cdot \mathbf{u}\), donde\(\mathbf{u}=\frac{\mathbf{d}}{\|\mathbf{d}\|}\)

Ahora generalizamos la formulación del trabajo en (\(\ref{4.3.2}\)) a la situación en la que un objeto\(P\) se mueve a lo largo de alguna curva\(C\) sujeto a una fuerza que depende continuamente de la posición (pero no depende del tiempo). Específicamente, representamos la fuerza por un campo vectorial continuo, digamos,\(F: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}\), y suponemos que\(P\) se mueve a lo largo de una curva\(C\) que tiene una parametrización suave\(\varphi: I \rightarrow \mathbb{R}^{n}\), donde\(I=[a, b]\). Ver Figura 4.3.2.

Figura\(\PageIndex{2}\): Objeto que\(P\) se mueve a lo largo de una curva\(C\) sujeto a una fuerza\(F\)

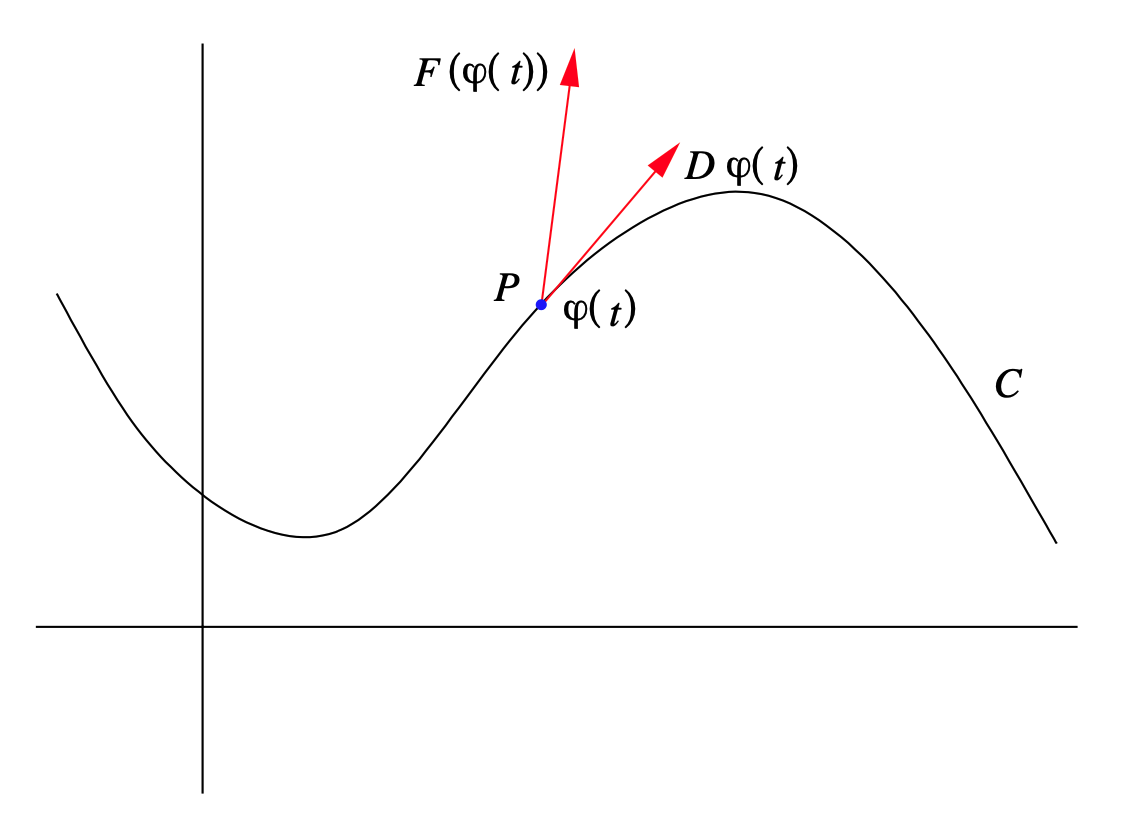
Para aproximar el trabajo realizado a\(F\) medida que\(P\) se mueve de\(\varphi(a)\) a\(\varphi(b)\) lo largo\(C\), primero\(I\) dividimos en subintervalos\(m\) iguales de longitud

\[ \Delta t=\frac{b-a}{m} \nonumber \]

con puntos finales\(t_{0}=a<t_{1}<t_{2}<\cdots<t_{m}=b\). Ahora en el momento\(t_{k}, k=0,1, \ldots, m-1, P\) se está moviendo en la dirección de\(D \varphi\left(t_{k}\right)\) a una velocidad de\(\left\|D \varphi\left(t_{k}\right)\right\|\), y así se moverá una distancia de aproximadamente a lo\(\left\|D \varphi\left(t_{k}\right)\right\| \Delta t\) largo del intervalo de tiempo\(\left[t_{k}, t_{k+1}\right]\). Así podemos aproximar el trabajo realizado por\(F\) como\(P\) se mueve de\(\varphi\left(t_{k}\right)\) a\(\varphi\left(t_{k+1}\right)\) por el trabajo realizado por la fuerza\(F\left(\varphi\left(t_{k}\right)\right)\) en movimiento\(P\) a lo largo del vector de desplazamiento\(D \varphi\left(t_{k}\right) \Delta t\), que es un vector de longitud\(\left\|D \varphi\left(t_{k}\right)\right\| \Delta t\) en la dirección de\(D \varphi\left(t_{k}\right)\). Es decir, si dejamos\(W_k\) denotar el trabajo realizado por\(F\) como\(P\) se mueve de\(\varphi\left(t_{k}\right)\) a\(\varphi\left(t_{k-1}\right)\), entonces

\[ W_{k} \approx F\left(\varphi\left(t_{k}\right)\right) \cdot D \varphi\left(t_{k}\right) \Delta t . \]

Si dejamos\(W\) denotar el trabajo total realizado por\(F\) como\(P\) se mueve a lo largo\(C\), entonces tenemos

\[ W=\sum_{k=0}^{m-1} W_{k}=\sum_{k=0}^{m-1} F\left(\varphi\left(t_{k}\right)\right) \cdot D \varphi\left(t_{k}\right) \Delta t . \label{4.3.4} \]

A medida que\(m\) aumenta, debemos esperar que la aproximación in (\(\ref{4.3.4}\)) se acerque\(W\). Además, dado que\(F(\varphi(t)) \cdot D \varphi(t)\) es una función continua de\(t\) y la suma in (\(\ref{4.3.4}\)) es una aproximación de regla de la izquierda para la integral definida de\(F(\varphi(t)) \cdot D \varphi(t)\) sobre el intervalo\([a,b]\), deberíamos tener

\[ W=\lim _{m \rightarrow \infty} \sum_{k=0}^{m-1} F\left(\varphi\left(t_{k}\right)\right) \cdot D \varphi\left(t_{k}\right) \Delta t=\int_{a}^{b} F(\varphi(t)) \cdot D \varphi(t) d t . \]

Ejemplo\(\PageIndex{1}\)

Supongamos que un objeto se mueve a lo largo de la curva\(C\) parametrizado por\(\varphi(t)=\left(t, t^{2}\right)\)\(-1 \leq t \leq 1\),, sujeto a la fuerza\(F(x, y)=(y, x)\). Entonces el trabajo realizado por a\(F\) medida que el objeto se mueve de\(\varphi(-1)=(-1,1)\) a\(\varphi(1)=(1,1)\) es

\ [\ begin {alineado}
W &=\ int_ {-1} ^ {1} F (\ varphi (t))\ cdot D\ varphi (t) d t\\
&=\ int_ {-1} ^ {1} F\ izquierda (t, t^ {2}\ derecha)\ cdot (1,2 t) d t\
&=\ int_ {-1} ^ {1} izquierda\ (t^ {2}, t\ derecha)\ cdot (1,2 t) d t\\
&=\ int_ {-1} ^ {1} 3 t^ {2} d t\\
&=\ izquierda.t^ {3}\ derecha|_ {-1} ^ {1}\\
&=2.
\ end {alineado}\]

Ejemplo\(\PageIndex{2}\)

La función\(\psi(t)=\left(\frac{t}{2}, \frac{t^{2}}{4}\right),-2 \leq t \leq 2\), es también una parametrización suave de la curva\(C\) en el ejemplo anterior. Usando la misma función de fuerza\(F\), tenemos

\ [\ begin {alineado}
\ int_ {-2} ^ {2} F (\ psi (t))\ cdot D\ psi (t) d t &=\ int_ {-2} ^ {2}\ izquierda (\ frac {t^ {2}} {4},\ frac {t} {2}\ derecha)\ cdot\ izquierda (\ frac {1} {2},\ frac {t} {2}\ derecha) d t\\
&=\ int_ {-2} ^ {2}\ frac {3 t^ {2}} {8} d t\\
&=\ izquierda. \ frac {t^ {3}} {8}\ derecha|_ {-2} ^ {2}\\
&=2.
\ end {alineado}\]

Este es el resultado que debemos esperar: siempre y cuando la curva sea atravesada solo una vez, el trabajo realizado por una fuerza cuando un objeto se mueve a lo largo de la curva debe depender únicamente de la curva y no de ninguna parametrización particular de la curva.

Tenemos que verificar el enunciado anterior en general antes de poder exponer nuestra definición de la integral de línea. Obsérvese que en estos dos ejemplos,\(\psi(t)=\varphi\left(\frac{t}{2}\right)\). En otras palabras,\(\psi(t)=\varphi(g(t))\), donde\(g(t)=\frac{t}{2}\) para\(-2 \leq t \leq 2\). En general, si\(\varphi(t)\), para\(t\) en un intervalo\([a,b]\), y\(\psi(t)\), para\(t\) en un intervalo\([c,d]\), son ambas parametrizaciones suaves de una curva\(C\) tal que cada punto en\(C\) corresponde exactamente a un punto adentro\(I\) y exactamente un punto adentro\(J\), entonces existe una función diferenciable\(g\) que mapea\(J\) sobre\(I\) tal que\(\psi(t)=\varphi(g(t))\). Definir tal\(g\) es sencillo: dado cualquiera\(t\) en\([c,d]\), encontrar el valor único\(s\) en\([a,b]\) tal que\(\varphi(s)=\psi(t)\) (tal valor\(s\) tiene que existir ya que\(C\) es la imagen de ambos\(\psi\) y\(\varphi\)). Entonces\(g(t) = s\). Demostrar que\(g\) es diferenciable no es tan fácil, y no vamos a proporcionar una prueba aquí. Sin embargo, suponiendo que ello\(g\) sea diferenciable, se deduce que para cualquier campo vectorial continuo\(F\),

\ begin {align}
\ int_ {c} ^ {d} F (\ psi (t))\ cdot D\ psi (t) d t &=\ int_ {c} ^ {d} F (\ varphi (g (t))\ cdot D (\ varphi\ circ g) (t)) d t\ nonumber\\
&=\ int_ {c} ^ {d} F\ izquierda (\ varphi (g (t))\ cdot D\ varphi (g (t)) g^ {\ prime} (t) d t\ derecha. \ label {4.3.6}
\ end {align}

Ahora si dejamos

\ [\ begin {aligned}
u &=g (t),\\
d u &=g^ {\ prime} (t) d t,
\ end {alineado}\]

en (\(\ref{4.3.6}\)), luego

\[ \int_{c}^{d} F(\psi(t)) \cdot D \psi(t) d t=\int_{a}^{b} F(\varphi(u)) \cdot D \varphi(u) d t \label{4.3.7} \]

si\(g(c)=a\) y\(g(d) = b\) (es decir,\(\varphi(a)=\psi(c)\) y\(\varphi(b)=\psi(d)\), y

\[ \int_{c}^{d} F(\psi(t)) \cdot D \psi(t) d t=\int_{b}^{a} F(\varphi(u)) \cdot D \varphi(u) d t=-\int_{b}^{a} F(\varphi(u)) \cdot D \varphi(u) d t \label{4.3.8} \]

si\(g(c)=b\) y\(g(d) = a\) (es decir,\(\varphi(a)=\psi(d)\) y\(\varphi(b)=\psi(c)\). Obsérvese que el segundo caso ocurre sólo si se\(\psi\) parametriza\(C\) en la dirección inversa de\(\varphi\), en cuyo caso decimos\(\psi\) es una orientación que revierte la reparametrización de\(\varphi\). En el primer caso, es decir, cuándo\(\varphi(a)=\psi(c)\) y\(\varphi(b)=\psi(d)\), decimos\(\psi\) es una orientación preservando la reparametrización de\(\varphi\). Nuestros resultados en (\(\ref{4.3.7}\)) y (\(\ref{4.3.8}\)) corresponden entonces a la noción física de que el trabajo realizado por una fuerza al mover un objeto a lo largo de una curva es lo negativo del trabajo realizado por la fuerza de mover el objeto a lo largo de la curva en dirección opuesta. A partir de ahora, al referirnos a una curva\(C\), asumiremos que se ha especificado alguna orientación, o dirección. Luego usaremos\(-C\) para referirnos a la curva que consiste en el mismo conjunto de puntos que\(C\), pero con la orientación inversa.

Integrales de línea

Ahora que sabemos que, a excepción de la dirección, el valor de la integral involucrada en el trabajo de computación no depende de la parametrización particular de la curva, podemos afirmar una definición matemática formal.

Definición\(\PageIndex{1}\)

Supongamos que\(C\) es una curva adentro\(\mathbb{R}^n\) con parametrización suave\(\varphi: I \rightarrow \mathbb{R}^{n}\), donde\(I = [a,b]\) es un intervalo adentro\(R\). Si\(F: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}\) es un campo vectorial continuo, entonces definimos la línea integral de\(F\) a lo largo\(C\), denotado

\[ \int_{C} F \cdot d s , \nonumber \]

por

\[ \int_{C} F \cdot d s=\int_{a}^{b} F(\varphi(t)) \cdot D \varphi(t) d t . \label{4.3.9} \]

Como consecuencia de nuestras anteriores observaciones, tenemos el siguiente resultado.

Proposición\(\PageIndex{1}\)

Utilizando la notación de la definición,

\[ \int_{C} F \cdot d s \nonumber \]

depende únicamente de la curva C y su orientación, no de la parametrización\(\varphi\). Por otra parte,

\[ \int_{-C} F \cdot d s=-\int_{C} F \cdot d s . \label{4.3.10} \]

Ejemplo\(\PageIndex{3}\)

Dejar\(C\) ser el círculo de la unidad centrado en el origen en\(\mathbb{R}^2\), orientado en el sentido contrario a las agujas del reloj, y dejar

\[ F(x, y)=\left(-\frac{y}{x^{2}+y^{2}}, \frac{x}{x^{2}+y^{2}}\right)=\frac{1}{x^{2}+y^{2}}(-y, x) . \nonumber \]

Para calcular la línea integral de\(F\) lo largo\(C\), primero necesitamos encontrar una parametrización suave de\(C\). Una de esas parametrización es

\[ \varphi(t)=(\cos (t), \sin (t)) \nonumber \]

para\(0 \leq t \leq 2 \pi\). Entonces

\ [\ begin {alineado}
\ int_ {C} F\ cdot d s &=\ int_ {0} ^ {2\ pi} F (\ cos (t),\ sin (t))\ cdot (-\ sin (t),\ cos (t)) d t\
&=\ int_ {0} ^ {2\ pi}\ frac {1} {\ cos ^ {2\ pi}} (t) +\ sin ^ {2} (t)} (-\ sin (t),\ cos (t))\ cdot (-\ sin (t),\ cos (t)) d t\
&=\ int_ {0} ^ {2\ pi}\ left (\ sin ^ {2 } (t) +\ cos ^ {2} (t)\ derecha) d t\\
&=\ int_ {0} ^ {2\ pi} d t\\
&=2\ pi.
\ end {alineado}\]

Tenga en cuenta que\(\psi(t)=(\sin (t), \cos (t)), 0 \leq t \leq 2 \pi\), parametriza\(-C\), a partir de la cual podemos calcular

\ [\ begin {alineado}
\ int_ {-C} F\ cdot d s &=\ int_ {0} ^ {2\ pi} F (\ sin (t),\ cos (t))\ cdot (\ cos (t), -\ sin (t)) d t\\
&=\ int_ {0} ^ {2\ pi}\ frac {1} {\ sin ^ {2} (t) +\ cos ^ {2} (t)} (-\ cos (t),\ sin (t))\ cdot (\ cos (t), -\ sin (t)) d t\
&=\ int_ {0} ^ {2\ pi}\ izquierda (-\ cos ^ {2 } (t) -\ sin ^ {2} (t)\ derecha) d t\\
&=-\ int_ {0} ^ {2\ pi} d t\\
&=-2\ pi,
\ end {alineado}\]

de acuerdo con la proposición anterior.

Una curva lisa por tramos es aquella que puede descomponerse en un número finito de curvas, cada una de las cuales tiene una parametrización suave. Si\(C\) es una curva lisa por tramos compuesta por la unión de las curvas\(C_{1}, C_{2}, \ldots, C_{m}\), entonces podemos extender la definición de la línea integral a\(C\) definiendo

\[ \int_{C} F \cdot d s=\int_{C_{1}} F \cdot d s+\int_{C_{2}} F \cdot d s+\cdots+\int_{C_{m}} F \cdot d s . \label{4.3.11} \]

El siguiente ejemplo ilustra este procedimiento.

Ejemplo\(\PageIndex{4}\)

Dejar\(C\) ser el rectángulo adentro\(\mathbb{R}^2\) con vértices en (0, 0), (2, 0), (2, 1), y (0, 1), orientado en sentido contrario a las agujas del reloj, y let\(F(x, y)=\left(y^{2}, 2 x y\right)\). Si dejamos\(C_1\),,\(C_2\)\(C_3\), y\(C_4\) ser los cuatro lados de\(C\), como se etiqueta en la Figura 4.3.3, entonces podemos parametrizar\(C_1\) por

\[ \alpha(t)=(t, 0) , \nonumber \]

\(0 \leq t \leq 2, C_{2}\)por

\[ \beta(t)=(2, t) , \nonumber \]

\(0 \leq t \leq 1, C_{3}\)por

\[ \gamma(t)=(2-t, 1) , \nonumber \]

\(0 \leq t \leq 2\), y\(C_4\) por

\[ \delta(t)=(0,1-t) , \nonumber \]

\(0 \leq t \leq 1\).

Figura\(\PageIndex{3}\): Rectángulo con orientación en sentido antihorario

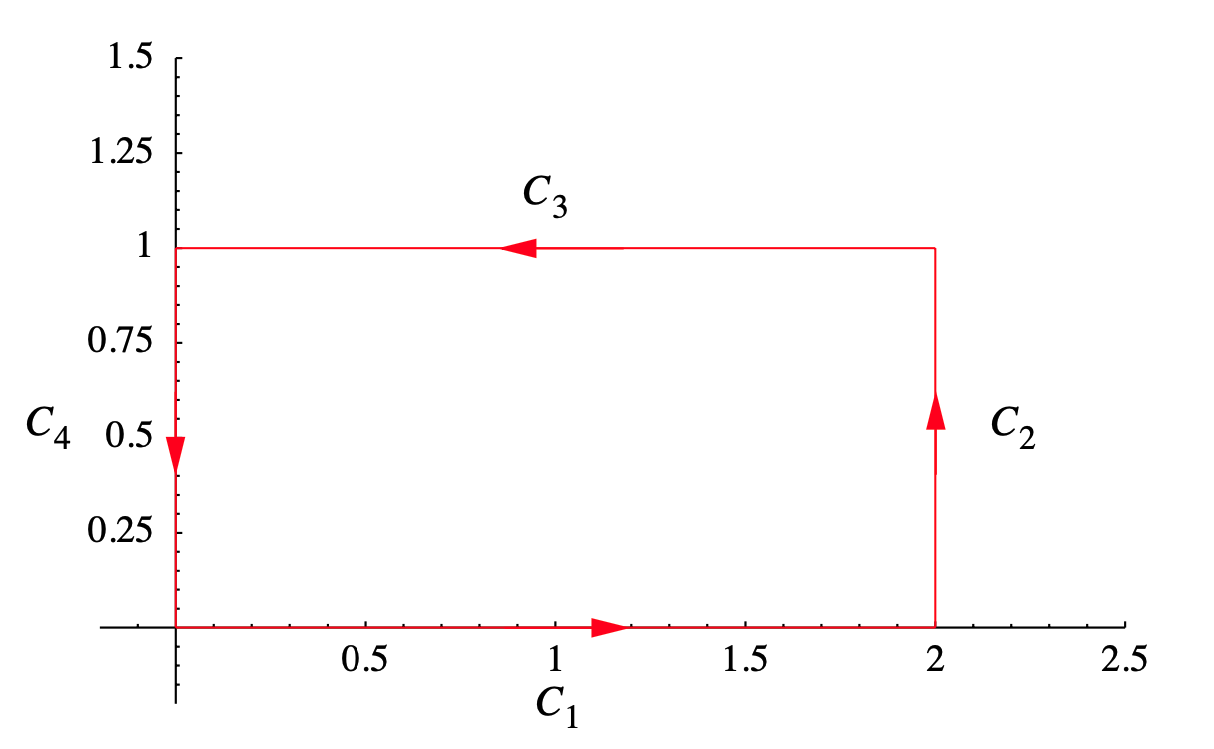
Entonces

\ [\ comenzar {alineado}
\ int_ {C} F\ cdot d s &=\ int_ {C_ {1}} F\ cdot d s+\ int_ {C_ {2}} F\ cdot d s+\ int_ {C_ {3}} F\ cdot d s+\ int_ {C_ {4}} F\ cdot d s\
&= _ {0} ^ {2} F (t, 0)\ cdot (1,0) d t+\ int_ {0} ^ {1} F (2, t)\ cdot (0,1) d t+\ int_ {0} ^ {2} F (2-t, 1)\ cdot (-1,0) d t\\
& amp; +\ int_ {0} ^ {1} F (0,1-t)\ cdot (0, -1) d t\\
=&\ int_ {0} ^ {2} (0,0)\ cdot (1,0) d t+\ int_ {0} ^ {1}\ izquierda (t^ {2}, 4 t\ derecha)\ cdot (0,1) d t+\ int_ {0} ^ {2} (1,4-2 t)\ cdot (-1,0) d t\\
&\ quad+\ int_ {0} ^ {1}\ izquierda ((1-t) ^ {2}, 0\ derecha)\ cdot (0, -1) d t\\
=&\ int_ {0} ^ {2} 0 d t+\ int_ {0} ^ {1} 4 t d t+\ int_ {0} ^ {2} (-1) d t+\ int_ {0} ^ {1} 0 d t\\
=&\ izquierda.2 t^ {2}\ derecha|_ {0} ^ {1} -2\\
=& 2-2\\
=& 0.
\ end {alineado}\]

Tenga en cuenta que sería un poco más sencillo parametrizar\(-C_3\) y\(-C_4\), utilizando

\[ \varphi(t)=(1, t) , \nonumber \]

\(0 \leq t \leq 2\), y

\[ \psi(t)=(t, 0) , \nonumber \]

\(0 \leq t \leq 1\), respectivamente, que parametrizar\(C_3\) y\(C_4\) directamente. Luego evaluaríamos

\[ \int_{C} F \cdot d s=\int_{C_{1}} F \cdot d s+\int_{C_{2}} F \cdot d s-\int_{-C_{3}} F \cdot d s-\int_{-C_{4}} F \cdot d s . \nonumber \]

Una nota sobre la notación

Supongamos que\(C\) es una curva suave en\(\mathbb{R}^n\), parametrizada por\(\varphi: I \rightarrow \mathbb{R}^{n}\)\(I = [a,b]\), donde, y dejar\(F: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}\) ser un campo vectorial continuo. Nuestra notación para la línea integral de\(F\) lo largo\(C\) viene de dejar\(s = \varphi (t) \), de la que tenemos

\[ \frac{d s}{d t}=D \varphi(t) , \nonumber \]

que podemos escribir, simbólicamente, como

\[ d s=D \varphi(t) d t . \nonumber \]

Ahora supongamos\(\varphi_{1}, \varphi_{2}, \ldots, \varphi_{n}\) y\(F_{1}, F_{2}, \ldots, F_{n}\) son las funciones componentes de\(\varphi\) y\(F\), respectivamente. Si dejamos

\ [\ comenzar {reunido}
x_ {1} =\ varphi_ {1} (t),\\
x_ {2} =\ varphi_ {2} (t),\\
\ vdots\\
x_ {n} =\ varphi_ {n} (t),
\ end {reunido}\]

entonces podemos escribir

\ [\ begin {align}
\ int_ {C} F\ cdot d s &=\ int_ {a} ^ {b} F (\ varphi (t))\ cdot D\ varphi (t) d t\ nonumber\\
&=\ int_ {a} ^ {b} F\ left (x_ {1} (t), x_ {2} (t),\ puntos, x_ {n} (t)\ derecha)\ cdot\ izquierda (\ varphi_ {1} ^ {\ prime} (t),\ varphi_ {2} ^ {\ prime} (t),\ ldots,\ varphi_ {n} ^ {\ prime} (t)\ derecha) d t\ nonumber\\
&\ izquierda. =\ int_ {a} ^ {b}\ izquierda (F_ {1}\ izquierda (x_ {1} (t), x_ {2} (t),\ ldots, x_ {n} (t)\ derecha)\ varphi_ {1} ^ {\ prime} (t) +F_ {2}\ izquierda (x_ {1} (t), x_ {2} (t),\ ldots, x_ {n} (t)\ derecha)\ varphi_ {2} ^ {\ prime} (t)\ derecha) +\ cDots+f_ {n}\ izquierda (x_ {1} (t), x_ {2} (t),\ ldots, x_ {n} (t)\ derecha)\ varphi_ {n} prime ^ {\} (t)\ derecha) d t\ nonumber\\
& =\ int_ {a} ^ {b} F_ {1}\ izquierda (x_ {1} (t), x_ {2} (t),\ ldots, x_ {n} (t)\ derecha)\ varphi_ {1} ^ {\ prime} (t) d t+\ int_ {a} ^ {b} F_ {2}\ izquierda (x_ {1} (t), x_ {2} (t),\ ldots, x_ {n} (t)\ derecha)\ varphi_ {2} ^ {\ prime} (t) d t+\ cdots+\ int_ {a} ^ {b} F_ {n}\ izquierda (x_ {1} (t), x_ {2} (t),\ lpuntos, x_ {} (t)\ derecha)\ varphi_ {n} ^ {\ prime} (t) d t. \ label {4.3.12}
\ end {align}\]

Suprimiendo la dependencia\(d x_{k}\) de\(t\)\(\varphi_{k}^{\prime}(t) d t, k=1,2, \ldots, n\), escribiendo y usando solo un solo signo integral, podemos reescribir (\(\ref{4.3.12}\)) como

\[ \int_{C} F_{1}\left(x_{1}, x_{2}, \ldots, x_{n}\right) d x_{1}+F_{2}\left(x_{1}, x_{2}, \ldots, x_{n}\right) d x_{2}+\cdots+F_{n}\left(x_{1}, x_{2}, \ldots, x_{n}\right) d x_{n} . \label{4.3.13} \]

Esta es una notación común y útil para una integral de línea.

Ejemplo\(\PageIndex{5}\)

Evaluaremos

\[ \int_{C} y d x+x d y+z^{2} d z , \nonumber \]

donde\(C\) está la parte de una hélice\(\mathbb{R}^3\) con ecuaciones paramétricas

\ [\ begin {aligned}
&x=\ cos (t),\\
&y=\ sin (t),\\
&z=t,
\ end {alineado}\]

\(0 \leq t \leq 2 \pi\). Tenga en cuenta que esto equivale a evaluar

\[ \int_{C} F \cdot d s , \nonumber \]

donde\(F: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}\) está el campo vectorial\(F(x, y, z)=\left(y, x, z^{2}\right)\). Tenemos

\ [\ begin {alineado}
\ int_ {C} y d x+x d y+z^ {2} d z &=\ int_ {0} ^ {2\ pi}\ izquierda (\ sin (t) (-\ sin (t)) +\ cos (t)\ cos (t) +t^ {2}\ derecha) d t\
&=\ int_ {0} ^ {2\ pi}\ izquierda (\ cos ^ {2} (t) -\ sin ^ {2} (t) +t^ {2}\ derecha) d t\
&=\ int_ {0} ^ {2\ pi}\ izquierda (\ cos (2 t) +t^ {2}\ derecha) d t\\
&=\ izquierda. \ frac {1} {2}\ sin (2 t)\ derecha|_ {0} ^ {2\ pi} +\ izquierda. \ frac {1} {3} t^ {3}\ derecha|_ {0} ^ {2\ pi}\\
&=\ frac {8\ pi^ {3}} {3}.
\ end {alineado}\]

Campos de degradado

Recordemos que si\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es\(C^1\), entonces\(\nabla f\) es un campo vectorial continuo encendido\(\mathbb{R}^n\). Supongamos\(\varphi: I \rightarrow \mathbb{R}^{n}, I=[a, b]\), es una parametrización suave de una curva\(C\). Luego, usando la regla de la cadena y el Teorema Fundamental del Cálculo,

\ [\ comenzar {alineado}
\ int_ {C}\ nabla f\ cdot d s &=\ int_ {a} ^ {b}\ nabla f (\ varphi (t))\ cdot D\ varphi (t) d t\
&=\ int_ {a} ^ {b}\ frac {d} {d} f (\ varphi (t)) d t\\
&=\ izquierda.f (\ varphi (t))\ derecha|_ {a} ^ {b}\\
&=f (\ varphi (b)) -f (\ varphi (a)).
\ end {alineado}\]

Teorema\(\PageIndex{1}\)

Si\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es\(C^1\) y\(\varphi: I \rightarrow \mathbb{R}^{n}, I=[a, b]\), es una parametrización suave de una curva\(C\), entonces

\[ \int_{C} \nabla f \cdot d s=f(\varphi(b))-f(\varphi(a)) . \label{4.3.14} \]

Tenga en cuenta que (\(\ref{4.3.14}\)) muestra que el valor de una integral de línea de un campo vectorial de gradiente depende únicamente de los puntos inicial y final de la curva, no de qué camino particular se toma entre estos dos puntos. Además, (\(\ref{4.3.14}\)) proporciona un medio simple para evaluar una integral de línea si el campo vectorial dado puede identificarse como el gradiente de una función de valor escalar. Otra consecuencia interesante es que si los puntos inicial y final de\(C\) son los mismos, es decir, si\(\mathbf{v}=\varphi(a)=\varphi(b)\), entonces

\[ \int_{C} \nabla f \cdot d s=f(\varphi(b))-f(\varphi(b))=f(\mathbf{v})-f(\mathbf{v})=0 . \]

A tales curvas las llamamos curvas cerradas. En palabras, la integral de línea de un campo vectorial de gradiente es 0 a lo largo de cualquier curva cerrada.

Ejemplo\(\PageIndex{6}\)

Si\(F(x, y)=(y, x)\), entonces

\[ F(x, y)=\nabla f(x, y) , \nonumber \]

donde\(f(x, y)=x y\). Por lo tanto, por ejemplo, para cualquier curva suave\(C\) que comience en (-1, 1) y termine en (1, 1) tenemos

\[ \int_{C} F \cdot d s=f(1,1)-f(-1,1)=1+1=2 . \nonumber \]

Obsérvese que esto concuerda con el resultado en nuestro primer ejemplo anterior, donde\(C\) estaba la parte de la parábola\(y=x^2\) extendiéndose de (−1, 1) a (1, 1).

Ejemplo\(\PageIndex{7}\)

Si\(f(x, y)=x y^{2}\), entonces

\[ \nabla f(x, y)=\left(y^{2}, 2 x y\right) . \nonumber \]

Si\(C\) es el rectángulo adentro\(\mathbb{R}^2\) con vértices en (0, 0), (2, 0), (2, 1), y (0, 1), entonces, ya que\(C\) es una curva cerrada,

\[ \int_{C} y^{2} d x+2 x y d y=0 , \nonumber \]

de acuerdo con un ejemplo anterior. Del mismo modo, si el círculo unitario\(E\) está\(\mathbb{R}^2\) centrado en el origen, entonces sabemos que

\[ \int_{E} y^{2} d x+2 x y d y=0 , \nonumber \]

sin necesidad de más cálculos.

En física,\(F\) se dice que un campo de fuerza es conservador si el trabajo realizado\(F\) al mover un objeto entre dos puntos cualesquiera depende únicamente de los puntos, y no del camino utilizado entre los dos puntos. En particular, hemos demostrado que si\(F\) es el gradiente de alguna función escalar\(f\), entonces\(F\) es un campo de fuerza conservador. Bajo ciertas condiciones en el dominio de\(F\), lo contrario también es cierto. Es decir, bajo ciertas condiciones, si\(F\) es un campo de fuerza conservador, entonces existe una función escalar\(f\) tal que\(F = \nabla f\). El ejercicio 9 explora una situación de este tipo en la que esto es cierto. La función\(f\) se conoce entonces como una función potencial.