2.1: Funciones de dos o tres variables
- Page ID
- 111350
En la Sección 1.8 discutimos las funciones vectoriales de una sola variable real. Ahora examinaremos las funciones de valor real de un punto (o vector) en\(\mathbb{R}^2\) o\(\mathbb{R}^ 3\). En su mayor parte estas funciones se definirán sobre conjuntos de puntos en\(\mathbb{R}^2\), pero habrá momentos en los que usaremos puntos en\(\mathbb{R}^ 3\), y también habrá momentos en los que será conveniente pensar en los puntos como vectores (o puntos terminales de vectores).
Una función de valor real f definida en un subconjunto\(D\) de\(\mathbb{R}^2\) es una regla que asigna a cada punto\(f(x,y)\) en\(D\) un número real\(f(x,y)\). El conjunto más grande posible\(D\)\(\mathbb{R}^2\) en el que\(f\) se define se llama el dominio de\(f\), y el rango de\(f\) es el conjunto de todos los números reales\(f(x,y)\) como\((x,y)\) varía sobre el dominio\(D\). Una definición similar se mantiene para las funciones\(f(x,y,z)\) definidas en puntos\((x,y,z)\) en\(\mathbb{R}^ 3\).
Ejemplo 2.1
El dominio de la función
\[\nonumber f(x,y)=xy\]
es todo el\(\mathbb{R}^2\), y el rango de\(f\) es todo de\(\mathbb{R}\).
Ejemplo 2.2
El dominio de la función
\[\nonumber f(x,y)=\dfrac{1}{x-y}\]
es todo\(\mathbb{R}^2\) excepto los puntos\((x,y)\) para los cuales\(x = y\). Es decir, el dominio es el conjunto\(D = \{(x, y) : x \ne y\}\). El rango de\(f\) es todos los números reales excepto 0.
Ejemplo 2.3
El dominio de la función
\[\nonumber f(x,y)=\sqrt{1-x^2-y^2}\]
es el conjunto\(D = \{(x, y) : x^ 2 + y^ 2 ≤ 1\}\), ya que la cantidad dentro de la raíz cuadrada no es negativa si y solo si 1−\((x^2 + y^2 ) ≥ 0\). Vemos que\(D\) consiste en todos los puntos dentro y dentro del círculo unitario en\(\mathbb{R}^2\) (a veces\(D\) se llama el disco de unidad cerrada). El rango de\(f\) es el intervalo [0,1] pulg\(\mathbb{R}\).
Ejemplo 2.4
El dominio de la función
\[\nonumber f(x,y,z)=e^{x+y-z}\]
es todo de\(\mathbb{R}^ 3\), y el rango de\(f\) es todos los números reales positivos.
Una función\(f (x, y)\) definida en\(\mathbb{R}^2\) suele escribirse como\(z = f (x, y)\), como se mencionó en la Sección 1.1, de manera que la gráfica de\(f (x, y)\) es el conjunto\(\{(x, y, z) : z = f (x, y)\}\) en\(\mathbb{R}^3\). Entonces vemos que esta gráfica es una superficie en\(\mathbb{R}^3\), ya que satisface una ecuación de la forma\(F(x, y, z) = 0\) (a saber, F (x, y, z) = f (x, y) − z). Las huellas de esta superficie en los planos\(z = c\), donde\(c\) varía sobre\(\mathbb{R}\), se llaman las curvas de nivel de la función. Equivalentemente, las curvas de nivel son los conjuntos de solución de las ecuaciones\(f (x, y) = c\), para\(c\) in\(\mathbb{R}\). Las curvas de nivel a menudo se proyectan sobre el\(xy\) plano para dar una idea de los diversos niveles de “elevación” de la superficie (como se hace en la topografía).
Ejemplo 2.5
La gráfica de la función
\[\nonumber f(x,y)=\dfrac{\sin \sqrt{x^2+y^2}}{\sqrt{x^2+y^2}}\]
se muestra a continuación. Tenga en cuenta que las curvas de nivel (mostradas tanto en la superficie como proyectadas sobre el\(xy\) plano) son grupos de círculos concéntricos.
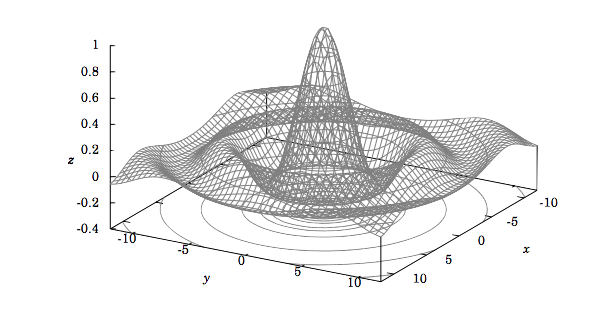
Quizás se esté preguntando qué pasa con la función en el Ejemplo 2.5 en el punto\((x, y) = (0,0)\), ya que tanto el numerador como el denominador son 0 en ese punto. La función no se define en (0,0), pero el límite de la función existe (y es igual a 1) como\((x, y)\) enfoques (0,0). Ahora vamos a exponer explícitamente lo que se entiende por el límite de una función de dos variables.
Definición 2.1
Dejar\((a,b)\) ser un punto en\(\mathbb{R}^2\), y dejar\(f(x,y)\) ser una función de valor real definida en algún conjunto que contiene\((a,b)\) (pero no necesariamente definido en\((a,b)\) sí mismo). Entonces decimos que el límite de\(f(x,y)\) iguales\(L\) como\((x,y)\) aproximaciones\((a,b)\), escrito como
\[\label{Eq2.1} \lim \limits_{(x,y) \to (a,b)}f(x,y)=L\]
si se le da alguna\(\epsilon > 0\), existe\(δ > 0\) tal que
\[\nonumber \lvert f(x,y)-L\rvert<\epsilon \text{ whenever } 0<\sqrt{(x-a)^2+(y-b)^2}<δ\]
Se puede hacer una definición similar para funciones de tres variables. La idea detrás de la definición anterior es que los valores de\(f(x, y)\) pueden acercarse arbitrariamente a\(L\) (es decir, dentro\(\epsilon\) de\(L\)) si elegimos\((x, y)\) suficientemente cerca a\((a,b)\) (es decir, dentro de un círculo centrado en\((a,b)\) con algún radio suficientemente pequeño δ).
Si recuerdas las pruebas “épsilon-delta” de límites de funciones de valor real de una sola variable, tal vez recuerdes lo incómodas que pueden ser, y cómo generalmente solo se pueden hacer fácilmente para funciones simples. En general, los casos multivariables son al menos igualmente incómodos de atravesar, por lo que no nos molestaremos con tales pruebas. En cambio, simplemente vamos a decir que cuando la función\(f (x, y)\) viene dada por una sola fórmula y se define en el punto\((a,b)\) (por ejemplo, no es una forma indeterminada como 0/0) entonces usted puede simplemente sustituir\((x, y) = (a,b)\) en la fórmula para\(f (x, y)\) para encontrar el límite.
Ejemplo 2.6
\[\nonumber \lim \limits_{(x,y) \to (1,2)} \dfrac{xy}{x^2+y^2}=\dfrac{(1)(2)}{1^2+2^2}=\dfrac{2}{5}\]
ya que\(f(x,y)=\dfrac{xy}{x^2+y^2}\) se define correctamente en el punto (1,2).
La mayor diferencia entre límites en una variable y límites en dos o más variables tiene que ver con cómo se aborda un punto. En el caso de una sola variable, la sentencia\(“x → a”\) significa que\(x\) se acerca al valor a desde dos direcciones posibles a lo largo de la línea numérica real (ver Figura 2.1.2 (a)). En dos dimensiones, sin embargo,\((x, y)\) puede acercarse a un punto\((a,b)\) a lo largo de un número infinito de caminos (ver Figura 2.1.2 (b)).
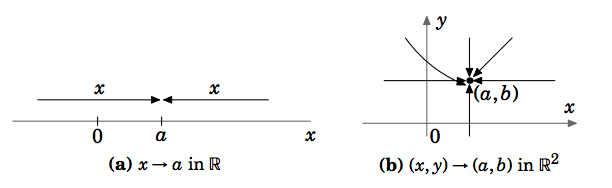
Ejemplo 2.7
\[\nonumber \lim \limits_{(x,y) \to (0,0)} \dfrac{xy}{x^2+y^2} \text{ does not exist}\]
Tenga en cuenta que no podemos simplemente sustituir\((x, y) = (0,0)\) a la función, ya que hacerlo da una forma indeterminada 0/0. Para demostrar que el límite no existe, mostraremos que la función se acerca a diferentes valores como\((x, y) \) enfoques (0,0) a lo largo de diferentes caminos en\(\mathbb{R}^2\). Para ver esto, supongamos que\((x, y) → (0,0)\) a lo largo del\(x\) eje positivo, así que\(y = 0\) a lo largo de ese camino. Entonces
\[\nonumber f(x,y)=\dfrac{xy}{x^2+y^2}=\dfrac{x0}{x^2+0^2}=0\]
a lo largo de ese camino (ya que\(x > 0\) en el denominador). Pero si\((x, y) → (0,0)\) a lo largo de la línea recta\(y = x\) por el origen\(x > 0\), pues, entonces vemos que
\[\nonumber f(x,y)=\dfrac{xy}{x^2+y^2}=\dfrac{x^2}{x^2+y^2}=\dfrac{1}{2}\]
lo que significa que\(f (x, y)\) se acerca a diferentes valores como\((x, y) → (0,0) \) a lo largo de diferentes caminos. De ahí que el límite no exista.
Los límites de las funciones multivariables de valor real obedecen a las mismas reglas algebraicas que en el caso de una sola variable, como se muestra en el siguiente teorema, que declaramos sin pruebas.
Teorema 2.1
Supongamos que eso\(\lim \limits_{(x,y) \to (a,b)}f(x,y)\) y\(\lim \limits_{(x,y) \to (a,b)}g(x,y)\) ambos existen, y eso\(k\) es algo escalar. Entonces:
- \(\lim \limits_{(x,y) \to (a,b)}\left [ f(x,y)\pm g(x,y)\right ] = \left [ \lim \limits_{(x,y) \to (a,b)}f(x,y)\right ] \pm \left [ \lim \limits_{(x,y) \to (a,b)}g(x,y)\right ] \)
- \(\lim \limits_{(x,y) \to (a,b)}kf(x,y)=k\left [ \lim \limits_{(x,y) \to (a,b)}f(x,y)\right ] \)
- \(\lim \limits_{(x,y) \to (a,b)}\left [ f(x,y)g(x,y)\right ] =\left [ \lim \limits_{(x,y) \to (a,b)}f(x,y)\right ] \left [ \lim \limits_{(x,y) \to (a,b)}g(x,y)\right ] \)
- \(\lim \limits_{(x,y) \to (a,b)}\dfrac{f(x,y)}{g(x,y)}=\dfrac{\lim \limits_{(x,y) \to (a,b)}f(x,y)}{\lim \limits_{(x,y) \to (a,b)}g(x,y)}\)si\(\lim \limits_{(x,y) \to (a,b)}g(x,y)\ne 0\)
- Si\(\lvert f(x,y)-L\rvert \le g(x,y)\) para todos\((x,y)\) y si\(\lim \limits_{(x,y) \to (a,b)}g(x,y)=0\), entonces\(\lim \limits_{(x,y) \to (a,b)}f(x,y)=L\)
Obsérvese que en la parte (e), basta con tener\(\lvert f(x,y)-L\rvert \le g(x,y)\) para todos\((x, y)\) “suficientemente cerca”\((a,b)\) (pero excluyéndose a\((a,b)\) sí mismo).
Ejemplo 2.8
Demostrar que
\[\nonumber \lim \limits_{(x,y) \to (0,0)}\dfrac{y^4}{x^2+y^2}=0\]
Dado que la sustitución\((x, y) = (0,0)\) en la función da la forma indeterminada 0/0, necesitamos un método alternativo para evaluar este límite. Utilizaremos el Teorema 2.1 (e). Primero, fíjate eso\(y^4 = (\sqrt{y^2})^4\) y así\(0\le y^4\le (\sqrt{x^2+y^2})^4\) para todos\((x, y)\). Pero\((\sqrt{x^2+y^2})^4=(x^2+y^2)^2\). Así, por todo\((x, y) \neq (0,0)\) lo que tenemos
\[\nonumber \lvert \dfrac{y^4}{x^2+y^2}\rvert \le \dfrac{(x^2+y^2)^2}{x^2+y^2}=x^2+y^2 → 0\,as\,(x,y)→(0,0)\]
Por lo tanto\(\lim \limits_{(x,y) \to (0,0)}\dfrac{y^4}{x^2+y^2}=0\).
La continuidad se puede definir de manera similar como en el caso de una sola variable.
Definición 2.2
Una función de valor real\(f (x, y)\) con dominio\(D\) en\(\mathbb{R}^2\) es continua en el punto\((a,b)\) en\(D\) if\(\lim \limits_{(x,y) \to (a,b)}f(x,y)=f(a,b)\). Decimos que\(f (x, y)\) es una función continua si es continua en cada punto de su dominio\(D\).
A menos que se indique lo contrario, puede asumir que todas las funciones que tratamos son continuas. De hecho, podemos modificar la función del Ejemplo 2.8 para que sea continua en todos\(\mathbb{R}^2\).
Ejemplo 2.9
Defina una función\(f (x, y)\) en todos de la\(\mathbb{R}^2\) siguiente manera:
\[\nonumber f(x,y)\cases{0 & \text{if } (x,y)=(0,0) \\[4pt] \nonumber \dfrac{y^4}{x^2+y^2} & \text{ if } (x,y)\neq (0,0) \\[4pt] }\]
Entonces\(f (x, y)\) está bien definido para todos\((x, y)\) en\(\mathbb{R}^2\) (es decir, no hay formas indeterminadas para ninguna\((x, y))\), y vemos que
\[\nonumber \lim \limits_{(x,y) \to (a,b)} f(x,y)=\dfrac{b^4}{a^2+b^2}=f(a,b) \text{ for } (a,b) \neq (0,0)\]
Así que desde
\[\nonumber \lim \limits_{(x,y) \to (0,0)} f(x,y)=0=f(0,0) \text{ by Example 2.8, }\]
entonces\(f(x,y)\) es continuo en todos\(\mathbb{R}^2\).


