3.E: Integrales Múltiples (Ejercicios)
- Page ID
- 111234
3.1: Integrales dobles
A
Para los Ejercicios 1-4, encuentra el volumen debajo de la superficie\(z = f (x, y)\) sobre el rectángulo\(R\).
3.1.1. \(f (x, y) = 4x y,\, R = [0,1]×[0,1] \)
3.1.2. \(f (x, y) = e^{ x+y} ,\, R = [0,1]×[−1,1] \)
3.1.3. \(f (x, y) = x^ 3 + y^ 2 ,\, R = [0,1]×[0,1] \)
3.1.4. \(f (x, y) = x^ 4 + x y+ y^ 3 ,\, R = [1,2]×[0,2]\)
Para los Ejercicios 5-12, evaluar la doble integral dada.
3.1.5. \(\int_0^1 \int_1^2 (1− y)x^ 2 \,dx \,d y\)
3.1.6. \(\int_0^1 \int_0^2 x(x+ y)\,dx \,d y\)
3.1.7. \(\int_0^2 \int_0^1 (x+2)\,dx \,d y\)
3.1.8. \(\int_{−1}^2 \int_{−1}^1 x(x y+\sin x)\,dx\, d y\)
3.1.9. \(\int_0^{\pi /2} \int_0^1 x y\cos (x^ 2 y)\,dx\, d y\)
3.1.10. \(\int_0^{\pi} \int_0^{π/2} \sin x \cos (y−π) \,dx\, d y\)
3.1.11. \(\int_0^2 \int_1^4 x y \,dx\, d y\)
3.1.12. \(\int_{-1}^1 \int_{-1}^2 1\,dx\, d y\)
3.1.13. Que\(M\) sea una constante. Demostrar que\(\int_c^d \int_a^b M\, dx \,d y = M(d − c)(b − a).\)
3.2: Integrales dobles sobre una región general
A
Para los Ejercicios 1-6, evaluar la doble integral dada.
3.2.1. \(\int_0^1 \int_{\sqrt{ x}}^1 24x^ 2 y \,d y\, dx\)
3.2.2. \(\int_0^π \int_0^y \sin x \,dx\, d y\)
3.2.3. \(\int_1^2 \int_0^{\ln x} 4x \,d y\, dx\)
3.2.4. \(\int_0^2 \int_0^{2y} e^ {y^ 2} \,dx \,d y\)
3.2.5. \(\int_0^{π/2} \int_0^y \cos x \sin y \,dx \,d y\)
3.2.6. \(\int_0^{∞} \int_0^{∞} x ye^{−(x^ 2+y^ 2 )}\, dx \,d y\)
3.2.7. \(\int_0^2 \int_0^y 1\,dx \,d y\)
3.2.8. \(\int_0^1 \int_0^{x^ 2} 2\,d y\, dx\)
3.2.9. Encuentra el volumen\(V\) del sólido delimitado por los tres planos de coordenadas y el plano\(x+ y+ z = 1\).
3.2.10. Encuentra el volumen\(V\) del sólido delimitado por los tres planos de coordenadas y el plano\(3x+2y+5z = 6\).
B
3.2.11. Explique por qué la doble integral\(\iint\limits_R 1\,d A\) da el área de la región\(R\). Por simplicidad, se puede suponer que\(R\) es una región del tipo que se muestra en la Figura 3.2.1 (a).
C
3.2.12. Demostrar que el volumen de un tetraedro con lados adyacentes mutuamente perpendiculares de longitudes\(a,\, b, \text{ and }c\), como en la Figura 3.2.6, es\(\frac{abc}{ 6}\). (Pista: Ejemplo mímico 3.5, y recordar de la Sección 1.5 cómo tres puntos no colineales determinan un plano. )
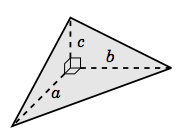
Figura 3.2.6
3.2.13. Mostrar cómo se puede utilizar el Ejercicio 12 para resolver el Ejercicio 10.
3.3: Integrales triples
A
Para los Ejercicios 1-8, evaluar la triple integral dada.
3.3.1. \(\int_0^3 \int_0^2 \int_0^1 x yz \,dx\, d y\, dz\)
3.3.2. \(\int_0^1 \int_0^x \int_0^y x yz \,dz\, d y\, dx\)
3.3.3. \(\int_0^π \int_0^x \int_0^{x y} x^ 2 \sin z \,dz\, d y\, dx\)
3.3.4. \(\int_0^1 \int_0^z \int_0^y ze^{ y^ 2} \,dx\, d y\, dz\)
3.3.5. \(\int_1^e \int_0^y \int_0^{1/y} x^ 2 z \,dx \,dz \,d y\)
3.3.6. \(\int_1^2 \int_0^{y^ 2} \int_0^{z^ 2} yz \,dx \,dz \,d y\)
3.3.7. \(\int_1^2 \int_2^4 \int_0^3 1\,dx \,d y\, dz\)
3.3.8. \(\int_0^1 \int_0^{1−x} \int_0^{1−x−y} 1\,dz\, d y\, dx\)
3.3.9. Que\(M\) sea una constante. \(\int_{z_1}^{z_2} \int_{y_1}^{y_2} \int_{x_1}^{x_2} M\, dx\, d y\, dz = M(z_2 − z_1)(y_2 − y_1)(x_2 − x_1)\)Demuéstralo.
B
3.3.10. Encuentra el volumen\(V\) del sólido\(S\) delimitado por los tres planos de coordenadas, delimitado arriba por el plano\(x+ y+ z = 2\) y delimitado por debajo por el plano\(z = x+ y\).
C
3.3.11. \(\int_a^b \int_a^z \int_a^y f (x)\,dx \,d y \,dz = \int_a^b \frac{(b−x)^ 2}{ 2} f (x)\,dx\)Demuéstralo. (Pista: Piense en cómo cambiar el orden de integración en la triple integral cambia los límites de la integración.)
3.4: Aproximación numérica de integrales múltiples
C
3.4.1. Escribir un programa que utilice el método Monte Carlo para aproximarse a la doble integral\(\iint\limits_R e^{ x y}\, d A\), donde\(R = [0,1]×[0,1]\). Mostrar la salida del programa para puntos\(N = 10,\, 100,\, 1000,\, 10000,\, 100000 \text{ and }1000000\) aleatorios.
3.4.2. Escribe un programa que utilice el método Montecarlo para aproximar la triple integral\ iiint\ Limits_s e^ {x yz}\, dV\), donde\(S = [0,1] × [0,1] × [0,1]\). Mostrar la salida del programa para puntos\(N = 10,\, 100,\, 1000,\, 10000,\, 100000 \text{ and }1000000\) aleatorios.
3.4.3. Repita el Ejercicio 1 con la región\(R = {(x, y) : −1 ≤ x ≤ 1,\, 0 ≤ y ≤ x^ 2 }\).
3.4.4. Repita el Ejercicio 2 con el sólido\(S = {(x, y, z) : 0 ≤ x ≤ 1,\, 0 ≤ y ≤ 1, \,0 ≤ z ≤ 1− x− y}\).
3.4.5. Utilice el método Montecarlo para aproximar el volumen de una esfera de radio 1.
3.4.6. Utilice el método de Monte Carlo para aproximar el volumen del elipsoide\(\frac{x^ 2}{ 9} + \frac{y^ 2}{ 4} + \frac{z^ 2}{ 1} = 1\).
3.5: Cambio de Variables en Integrales Múltiples
A
3.5.1. Encuentra el volumen\(V\) dentro del paraboloide\(z = x^ 2 + y^ 2 \text{ for }0 ≤ z ≤ 4\).
3.5.2. Encuentra el volumen\(V\) dentro del cono\(z = \sqrt{ x^ 2 + y^ 2}\) para\(0 ≤ z ≤ 3\).
B
3.5.3. Encuentra el volumen\(V\) del sólido dentro de ambos\(x^ 2 + y^ 2 + z^ 2 = 4\) y\(x^ 2 + y^ 2 = 1\).
3.5.4. Encuentra el volumen\(V\) dentro tanto de la esfera\(x^ 2 + y^ 2 + z^ 2 = 1\) como del cono\(z = \sqrt{ x^ 2 + y^ 2}\).
3.5.5. Demostrar Ecuación (3.25).
3.5.6. Demostrar Ecuación (3.26).
3.5.7. Evaluar\(\iiint\limits_R \sin \left ( \frac{x+y}{ 2} \right ) \cos \left ( \frac{x−y}{ 2} \right ) \,d A\), donde\(R\) está el triángulo con vértices\((0,0),\, (2,0) \text{ and }(1,1)\). (Pista: Usar el cambio de variables\(u = (x+ y)/2,\, v = (x− y)/2.\))
3.5.8. Encuentra el volumen del sólido delimitado por\(z = x^ 2 + y^ 2 \text{ and }z^ 2 = 4(x^ 2 + y^ 2 )\).
3.5.9. Encuentra el volumen dentro del cilindro elíptico\(\frac{x^ 2}{ a^ 2} + \frac{y^ 2}{ b^ 2} = 1 \text{ for } 0 ≤ z ≤ 2\).
C
3.5.10. Mostrar que el volumen dentro del elipsoide\(\frac{x^ 2}{ a^ 2} + \frac{y^ 2}{ b^ 2} + \frac{z^ 2}{ c^ 2} = 1 \text{ is }\frac{4πabc}{ 3}\). (Pista: Usa el cambio de variables\(x = au,\, y = bv,\, z = cw\), luego considera el Ejemplo 3.12. )
3.5.11. Mostrar que la función Beta, definida por
\[B(x, y) = \int_0^1 t^{ x−1} (1− t)^{ y−1} dt ,\text{ for }x > 0,\, y > 0,\]
satisface la relación\(B(y, x) = B(x, y) \text{ for }x > 0,\, y > 0.\)
3.5.12. Usando la sustitución\(t = u/(u +1)\), muestra que la función Beta se puede escribir como
\[B(x, y) = \int_0^∞ \frac{u^{ x−1}}{ (u +1)^{x+y}}\, du ,\text{ for }x > 0,\, y > 0.\]
3.6: Aplicación: Centro de Masa
A
Para los Ejercicios 1-5, encuentra el centro de masa de la región\(R\) con la función de densidad dada\(δ(x, y)\).
3.6.1. \(R = {(x, y) : 0 ≤ x ≤ 2,\, 0 ≤ y ≤ 4 },\, δ(x, y) = 2y\)
3.6.2. \(R = {(x, y) : 0 ≤ x ≤ 1,\, 0 ≤ y ≤ x 2 },\, δ(x, y) = x+ y \)
3.6.3. \(R = {(x, y) : y ≥ 0,\, x^ 2 + y^ 2 ≤ a^ 2 },\, δ(x, y) = 1\)
3.6.4. \(R = {(x, y) : y ≥ 0,\, x ≥ 0,\, 1 ≤ x^ 2 + y^ 2 ≤ 4 },\, δ(x, y) = \sqrt{ x^ 2 + y^ 2}\)
3.6.5. \(R = {(x, y) : y ≥ 0,\, x^ 2 + y^ 2 ≤ 1 },\, δ(x, y) = y\)
B
Para Ejercicios 6-10, encuentra el centro de masa del sólido\(S\) con la función de densidad dada\(δ(x, y, z)\).
3.6.6. \(S = {(x, y, z) : 0 ≤ x ≤ 1,\, 0 ≤ y ≤ 1,\, 0 ≤ z ≤ 1 },\, δ(x, y, z) = x yz\)
3.6.7. \(S = {(x, y, z) : z ≥ 0,\, x^ 2 + y^ 2 + z^ 2 ≤ a^ 2 },\, δ(x, y, z) = x^ 2 + y^ 2 + z^ 2\)
3.6.8. \(S = {(x, y, z) : x ≥ 0,\, y ≥ 0,\, z ≥ 0,\, x^ 2 + y^ 2 + z^ 2 ≤ a^ 2 },\, δ(x, y, z) = 1\)
3.6.9. \(S = {(x, y, z) : 0 ≤ x ≤ 1,\, 0 ≤ y ≤ 1,\, 0 ≤ z ≤ 1 },\, δ(x, y, z) = x^ 2 + y^ 2 + z^ 2\)
3.6.10. \(S = {(x, y, z) : 0 ≤ x ≤ 1,\, 0 ≤ y ≤ 1,\, 0 ≤ z ≤ 1− x− y},\, δ(x, y, z) = 1\)
3.7: Aplicación: Probabilidad y Valor Esperado
B
3.7.1. Evalúa la integral\(\int_{−\infty}^{\infty} e^{ −x^ 2}\, dx\) usando cualquier cosa que hayas aprendido hasta ahora.
3.7.2. Para\(σ > 0 \text{ and }µ > 0\), evaluar\(\int_{\infty}^{−\infty} \frac{1}{ σ \sqrt{ 2π}} e^{ −(x−µ)^ 2 /2σ^ 2} dx\).
3.7.3. Mostrar que\(EY = \frac{n}{ n+1}\) en el Ejemplo 3.18
C
3.7.4. Escriba un programa de computadora (en el idioma de su elección) que verifique los resultados en el Ejemplo 3.18 para el caso\(n = 3\) tomando grandes cantidades de muestras.
3.7.5. Repita el Ejercicio 4 para el caso cuando\(n = 4\).
3.7.6. Para variables aleatorias continuas\(X, Y \text{ with joint p.d.f. }f (x, y)\), defina los segundos momentos\(E(X^ 2 ) \text{ and }E(Y^ 2 )\) por
\[E(X^ 2 ) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x^ 2 f (x, y)\,dx\, d y \text{ and }E(Y^ 2 ) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} y^ 2 f (x, y)\,dx \,d y ,\]
y las varianzas Var\((X)\) y Var\((Y)\) por
\[\text{Var}(X) = E(X^ 2 )−(EX)^ 2 \text{ and Var}(Y) = E(Y^ 2 )−(EY)^ 2 .\]
Encuentra Var\((X)\) y Var\((Y)\) para\(X\) y\(Y\) como en el Ejemplo 3.18.
3.7.7. Continuando con el Ejercicio 6, la correlación\(ρ \text{ between }X \text{ and }Y\) se define como
\[ρ = \frac{E(XY)−(EX)(EY)}{ \sqrt{ \text{Var}(X)\text{Var}(Y)}} ,\]
donde\(E(XY) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x y \,f (x, y)\,dx\, d y\). Encuentra\(ρ\) por\(X \text{ and }Y\) como en el Ejemplo 3.18.
(Nota: La cantidad\(E(XY)−(EX)(EY)\) se llama la covarianza de\(X\) y\(Y\).)
3.7.8. En el Ejemplo 3.17 cambiaría la respuesta si\((0,100)\) se usa el intervalo en lugar de\((0,1)\)? Explique.


