4.3: Teorema de Green
- Page ID
- 111287
Ahora veremos una manera de evaluar la integral de línea de un campo vectorial suave alrededor de una curva cerrada simple. Un campo vectorial\(\textbf{f}(x, y) = P(x, y)\textbf{i} + Q(x, y)\textbf{j}\) es suave si su componente funciona\(P(x, y)\) y\(Q(x, y)\) son suaves. Utilizaremos el Teorema de Green (a veces llamado Teorema de Green en el plano) para relacionar la línea integral alrededor de una curva cerrada con una doble integral sobre la región dentro de la curva:
Teorema 4.7: Teorema de Green
Let\(R\) Ser una región en\(\mathbb{R}^2\) cuyo límite es una simple curva cerrada\(C\) que es lisa por tramos. Let\(\textbf{f}(x, y) = P(x, y)\textbf{i}+Q(x, y)\textbf{j}\) Ser un campo vectorial suave definido en ambos\(R\) y\(C\). Entonces
\[\oint_C \textbf{f}\cdot d\textbf{r} = \iint\limits_R \left ( \dfrac{∂Q}{ ∂x} - \dfrac{∂P}{ ∂y} \right )\,dA, \label{Eq4.21}\]
donde\(C\) se recorre de manera que\(R\) esté siempre en el lado izquierdo de\(C\).
Prueba: Vamos a probar el teorema en el caso de una región simple\(R\), es decir, donde la curva límite se\(C\) puede escribir como de dos\(C = C_1 \cup C_2\) maneras distintas:
\[\begin{align} C_1 &= \text{ the curve }y = y_1(x)\text{ from the point }X_1 \text{ to the point }X_2 \label{Eq4.22} \\[4pt] C_2 &=\text{ the curve }y = y_2(x) \text{ from the point }X_2 \text{ to the point } X_1 , \label{Eq4.23} \\[4pt] \end{align}\]
donde\(X_1\) y\(X_2\) son los puntos\(C\) más alejados a la izquierda y a la derecha, respectivamente; y
\[\begin{align} C_1 &= \text{ the curve }x = x_1(y)\text{ from the point }Y_2 \text{ to the point } Y_1 \label{Eq4.24} \\[4pt] C_2 &= \text{ the curve } x = x_2(y)\text{ from the point } Y_1 \text{ to the point }Y_2,\label{Eq4.25} \\[4pt] \end{align}\]
donde\(Y_1\) y\(Y_2\) son los puntos más bajos y más altos, respectivamente, en\(C\). Ver Figura 4.3.1.
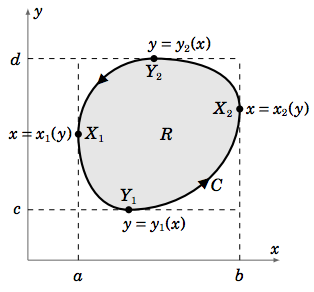
Integrar\(P(x, y)\) alrededor\(C\) usando la representación\(C = C_1 \cup C_2\) dada por la Ecuación\ ref {Eq4.23} y Ecuación\ ref {Eq4.24}.
Ya que\(y = y_1(x) \text{ along }C_1\) (como\(x\) va desde\(a \text{ to }b)\) y\(y = y_2(x) \text{ along }C_2\) (como\(x\) va desde\(b \text{ to }a)\), como vemos en la Figura 4.3.1, entonces tenemos
\[\nonumber \begin{align} \oint_C P(x, y)\,dx&=\int_{C_1}P(x, y)\,dx+\int_{C_2}P(x, y)\,dx \\[4pt] \nonumber &=\int_a^b P(x, y_1(x))\,dx+\int_b^a P(x, y_2(x))\,dx \\[4pt] \nonumber &=\int_a^b P(x, y_1(x))\,dx - \int_a^b P(x, y_2(x))\,dx \\[4pt] \nonumber &=-\int_a^b (P(x, y_2(x)) - P(x, y_1(x)))\, dx \\[4pt] \nonumber &=-\int_a^b \left ( P(x, y) \Big |_{y=y_1(x)}^{y=y_2(x)} \right )\,dx \\[4pt] \nonumber &=-\int_a^b \int_{y_1(x)}^{y_2(x)} \dfrac{∂P(x, y)}{ ∂y}\,dy\,dx \text{ (by the Fundamental Theorem of Calculus)} \\[4pt] &=-\iint\limits_R \dfrac{∂P}{ ∂y}\,dA. \\[4pt] \label{Eq4.26} \end{align}\]
Así mismo, integre\(Q(x, y)\) alrededor\(C\) usando la representación\(C = C_1 \cup C_2\) dada por la Ecuación\ ref {Eq4.25} y la Ecuación\ ref {Eq4.26}. Desde\(x = x_1(y) \text{ along }C_1\) (como\(y\) va de\(d\) a\(c\)) y\(x = x_2(y) \text{ along }C_2\) (como\(y\) va de\(c\) a\(d\)), como vemos en la Figura 4.3.1, entonces tenemos
\[\nonumber \begin{align} \oint_C Q(x, y)\,dy&=\int_{C_1}Q(x, y)\,dy+\int_{C_2}Q(x, y)\,dy \\[4pt] \nonumber &=\int_d^c Q(x_1(y), y)\,dy+\int_c^d Q(x_2(y), y)\,dy \\[4pt] \nonumber &=-\int_c^d Q(x_1(y), y)\,dy + \int_c^d Q(x_2(y), y)\,dy \\[4pt] \nonumber &=\int_c^d (Q(x_2(y), y) - Q(x_1(y), y))\, dy \\[4pt] \nonumber &=\int_c^d \left ( Q(x, y) \Big |_{x=x_1(y)}^{x=x_2(y)} \right )\,dy \\[4pt] \nonumber &=\int_c^d \int_{x_1(y)}^{x_2(y)} \dfrac{∂Q(x, y)}{ ∂x}\,dx\,dy \text{ (by the Fundamental Theorem of Calculus)} \\[4pt] \nonumber &=\iint\limits_R \dfrac{∂Q}{ ∂x}\,dA,\text{ and so} \\[4pt] \end{align}\]
\[\nonumber \begin{align} \oint_C \textbf{f}\cdot d\textbf{r} &= \oint_C P(x, y)\,dx + \oint_C Q(x, y)\,d y \\[4pt] \nonumber &= -\iint_R \dfrac{∂P}{ ∂y}\,dA + \iint_R \dfrac{∂Q}{∂x}\,dA \\[4pt] \nonumber &= \iint_R \left ( \dfrac{∂Q}{ ∂x}-\dfrac{∂P}{ ∂y} \right ) \,dA. \\[4pt] \end{align}\]
\(\tag{\(\textbf{QED}\)}\)
Aunque probamos el Teorema de Green solo para una región simple\(R\), el teorema también se puede probar para regiones más generales (digamos, una unión de regiones simples).
Ejemplo 4.7
Evaluar\(\oint_C (x^2 + y^2 )\,dx+2x y\, d y\), donde\(C\) está el límite (atravesado en sentido antihorario) de la región\(R = {(x, y) : 0 ≤ x ≤ 1, 2x^2 ≤ y ≤ 2x}\).
\(R\)es la región sombreada en la Figura 4.3.2. Por el teorema de Green\(P(x, y) = x^2 + y^2 \text{ and }Q(x, y) = 2x y\), para, tenemos
\[\nonumber \begin{align} \oint_C (x^2+y^2)\,dx+2x y \,d y &=\iint_R \left ( \dfrac{∂Q}{ ∂x}-\dfrac{∂P}{ ∂y} \right ) \, dA \\[4pt] \nonumber &=\iint_R (2y−2y)\,d A = \iint_R 0\,dA = 0. \\[4pt] \end{align}\]
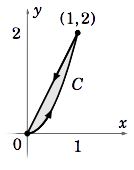
De hecho ya sabíamos que la respuesta era cero. Recordemos del Ejemplo 4.5 en la Sección 4.2 que el campo vectorial\(\textbf{f}(x, y) = (x^2 + y^2 )\textbf{i}+2x y\textbf{j}\) tiene una función potencial\(F(x, y) = \dfrac{1}{3} x^3 + x y^2\), y así\(\oint_C \textbf{f}\cdot d\textbf{r} = 0\) por Corolario 4.6.
Ejemplo 4.8
Vamos\(\textbf{f}(x, y) = P(x, y)\textbf{i}+Q(x, y)\textbf{j}\), donde
\[\nonumber P(x, y) =\dfrac{-y}{x^2+y^2} \text{ and }Q(x, y) =\dfrac{x}{x^2+y^2},\]
y vamos\(R = {(x, y) : 0 < x^2 + y^2 ≤ 1}\). Para la curva límite\(C : x^2 + y^2 = 1\), atravesada en sentido antihorario, se mostró en el Ejercicio 9 (b) en la Sección 4.2 que\(\oint_C \textbf{f}\cdot d\textbf{r} = 2π\). Pero
\[\nonumber \dfrac{∂Q }{∂x} = \dfrac{y^2+x^2}{(x^2+y^2)^2} = \dfrac{∂P }{∂y} \Rightarrow \iint\limits_R \left ( \dfrac{∂Q}{ ∂x} - \dfrac{ ∂P}{ ∂y} \right )\,dA= \iint\limits_R 0\,dA = 0\]
Esto parecería contradecir el Teorema de Green. No obstante, tenga en cuenta que no\(R\) es toda la región encerrada\(C\), ya que el punto no\((0,0)\) está contenido en\(R\). Es decir,\(R\) tiene un “agujero” en el origen, por lo que el Teorema de Green no aplica.
Si modificamos la región\(R\) para que sea el anillo\(R = {(x, y) : 1/4 ≤ x^2 + y^2 ≤ 1}\) (ver Figura 4.3.3), y tomamos el “límite”\(C \text{ of }R \text{ to be }C = C_1 \cup C_2\), donde\(C_1\) está el círculo unitario\(x^2 + y^2 = 1\) atravesado en sentido antihorario y\(C_2\) es el círculo\(x^2 + y^2 = 1/4\) atravesado en sentido horario, entonces se puede mostrar (ver Ejercicio 8) que
\[\nonumber \oint_C \textbf{f} \cdot d\textbf{r} = 0 \]
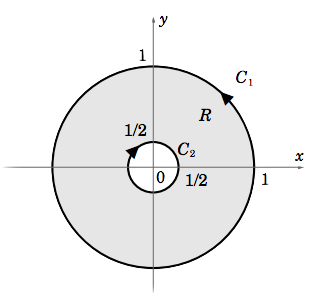
Todavía tendríamos\(\iint\limits_R \left ( \dfrac{∂Q}{∂x} − \dfrac{∂P}{ ∂y } \right )\,d A = 0\), así que para esto\(R\) tendríamos
\[\nonumber \oint_C \textbf{f}\cdot d\textbf{r} = \iint\limits_R \left ( \dfrac{∂Q}{ ∂x} - \dfrac{∂P}{ ∂y} \right ) \, dA,\]
lo que demuestra que el Teorema de Green se sostiene para la región anular\(R\).
Resulta que el Teorema de Green se puede extender para multiplicar regiones conectadas, es decir, regiones como el anillo en el Ejemplo 4.8, que tienen una o más regiones recortadas del interior, a diferencia de que se cortan puntos discretos. Para tales regiones, se recorren el límite “exterior” y los límites “interiores” de manera que siempre\(R\) se encuentre en el lado izquierdo.
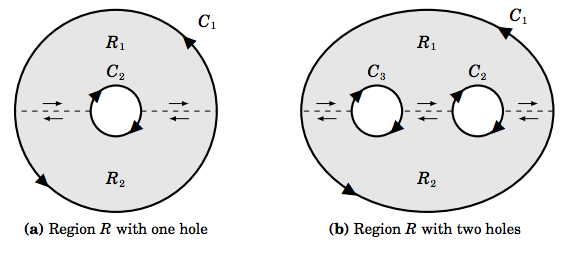
La idea intuitiva de por qué el Teorema de Green se mantiene para múltiples regiones conectadas se muestra en la Figura 4.3.4 anterior. La idea es cortar “hendiduras” entre los límites de una región conectada de\(R\) manera que\(R\) se divide en subregiones que no tienen ningún “agujero”. Por ejemplo, en la Figura 4.3.4 (a) la región\(R\) es la unión de las regiones\(R_1 \text{ and }R_2\), las cuales están divididas por las hendiduras indicadas por las líneas discontinuas. Esas hendiduras forman parte del límite de ambas\(R_1 \text{ and }R_2\), y atravesamos entonces de la manera señalada por las flechas. Observe que a lo largo de cada hendidura el límite de\(R_1\) se atraviesa en la dirección opuesta a la de\(R_2\), lo que significa que las integrales de línea de\ textbf {f} a lo largo de esas hendiduras se cancelan entre sí. Como\(R_1 \text{ and }R_2\) no tienen agujeros en ellos, entonces el Teorema de Green se sostiene en cada subregión, de manera que
\[\nonumber \oint_{bdy\,of\,R_1}\textbf{f} \cdot d\textbf{r} = \iint\limits_{R_1}\left (\dfrac{ ∂Q }{∂x} - \dfrac{∂P }{∂y} \right )\,dA \text{ and }\oint_{bdy\,of\,R_2}\textbf{f}\cdot d\textbf{r} = \iint\limits{R_2} \left ( \dfrac{∂Q }{∂x} - \dfrac{∂P}{ ∂y} \right )\,dA.\]
Pero como las integrales de línea a lo largo de las ranuras se cancelan, tenemos
\[\nonumber \oint_{C_1 \cup C_2} \textbf{f}\cdot d\textbf{r} = \oint_{bdy\,of\,R_1} \textbf{f} \cdot d\textbf{r} +\oint_{bdy\,of\,R_2}\textbf{f}\cdot d\textbf{r},\]
y así
\[\nonumber \oint_{C_1 \cup C_2} \textbf{f}\cdot d\textbf{r} = \iint\limits_{R_1} \left ( \dfrac{∂Q}{ ∂x} − \dfrac{∂P}{ ∂y} \right ) \,dA + \iint\limits_{R_2} \left ( \dfrac{∂Q}{ ∂x} − \dfrac{∂P}{ ∂y} \right ) \,dA = \iint\limits_R \left ( \dfrac{∂Q}{ ∂x} - \dfrac{∂P }{∂y} \right ) \,dA,\]
lo que demuestra que el Teorema de Green sostiene en la región\(R\). Un argumento similar muestra que el teorema se mantiene en la región con dos agujeros mostrados en la Figura 4.3.4 (b).
Sabemos por Corolario 4.6 que cuando un campo vectorial suave\(\textbf{f}(x, y) = P(x, y)\textbf{i}+Q(x, y)\textbf{j}\) en una región\(R\) (cuyo límite es una curva lisa por tramos, simple cerrada\(C\)) tiene un potencial en\(R\), entonces\(\oint_C \textbf{f}\cdot d\textbf{r} = 0\). Y si el potencial\(F(x, y)\) es suave en\(R\), entonces\(\dfrac{∂F}{ ∂x} = P \text{ and }\dfrac{∂F}{ ∂y} = Q\), y así sabemos que
\[\nonumber \dfrac{∂^2F }{∂y∂x} = \dfrac{∂^2F}{ ∂x∂y} \Rightarrow \dfrac{∂P}{ ∂y} = \dfrac{∂Q }{∂x}\text{ in }R\]
Por el contrario, si\(\dfrac{∂P}{ ∂y} = \dfrac{∂Q}{ ∂x}\) en\(R\) entonces
\[\nonumber \oint_C \textbf{f} \cdot d\textbf{r} = \iint\limits_R \left ( \dfrac{∂Q }{∂x}-\dfrac{∂P }{∂y} \right ) \,dA \iint\limits_R 0\,dA = 0 \]
Para una región simplemente conectada\(R\) (es decir, una región sin agujeros), se puede mostrar lo siguiente:
Las siguientes declaraciones son equivalentes para una región simplemente conectada\(R\) en\(\mathbb{R}^2\):
- \(\textbf{f}(x, y) = P(x, y)\textbf{i}+Q(x, y)\textbf{j} \)tiene un potencial suave\(F(x, y)\) en\(R\)
- \(\int_C \textbf{f}\cdot d\textbf{r}\)es independiente de la trayectoria para cualquier curva\(C\) en\(R\)
- \(\oint_C \textbf{f} \cdot d\textbf{r} = 0\)para cada curva cerrada simple\(C\) en\(R\)
- \(\dfrac{ ∂P}{ ∂y} = \dfrac{∂Q }{∂x} \)en\(R\) (en este caso, la forma diferencial\(P dx+Q d y\) es exacta)


