1.8: Una interpretación geométrica de las derivadas

Última actualización
Guardar como PDF

Page ID: 117180

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Recordemos que si$y=f(x),$ entonces, para cualquier número real$\Delta x$,

\[\frac{\Delta y}{\Delta x}=\frac{f(x+\Delta x)-f(x)}{\Delta x}\]es la tasa promedio de cambio de$y$ con respecto a$x$ sobre el intervalo$[x, x+\Delta x]$ (ver$(1.2 .7)) .$ Ahora si la gráfica de$y$ es una línea recta, es decir, si$f(x)=m x+b$ para algunos números reales$m$ y$b,$ luego$(1.8 .1)$ es$m,$ la pendiente de la línea. De hecho, una línea recta se caracteriza porque el hecho$(1.8 .1)$ es el mismo para cualquier valor de$x$ y$\Delta x .$ Además,$(1.8 .1)$ permanece igual cuando$\Delta x$ es infinitesimal; es decir, la derivada de$y$ con respecto a$x$ es la pendiente de la línea. Para otras funciones diferenciables$f,$ el valor de$(1.8 .1)$ depende de ambos$x$ y$\Delta x .$ Sin embargo, para los valores infinitesimales de$\Delta x,$ la sombra de$(1.8 .1),$ eso es, la derivada$\frac{d y}{d x},$ depende$x$ solo de. De ahí que sea razonable pensar en la pendiente de la curva$y=f(x)$ en un punto$x .$ Mientras que la pendiente de una recta es constante de punto a punto, para otras funciones diferenciables el valor de la pendiente de la curva variará de punto a punto.$\frac{d y}{d x}$ Si$f$ es diferenciable en un punto$a,$ llamamos a la línea con pendiente que$f^{\prime}(a)$ pasa por$(a, f(a))$ la línea tangente a la gráfica de$f$ at Es$(a, f(a)) .$ decir, la línea tangente a la gráfica de$y=f(x)$ at$x=a$ es la línea con ecuación\[y=f^{\prime}(a)(x-a)+f(a) .\] De ahí un línea tangente a la gráfica de una función$f$ es una línea a través de un punto en la gráfica$f$ cuya pendiente es igual a la pendiente de la gráfica en ese punto.

Ejemplo$\PageIndex{1}$

Si$f(x)=x^{5}-6 x^{2}+5,$ entonces

\[f^{\prime}(x)=5 x^{4}-12 x .\]En particular,$f^{\prime}\left(-\frac{1}{2}\right)=\frac{101}{16},$ y así la ecuación de la línea tangente a la gráfica de$f$ at$x=-\frac{1}{2}$ es\[y=\frac{101}{6}\left(x+\frac{1}{2}\right)+\frac{111}{32} .\] Ver Figura 1.8.1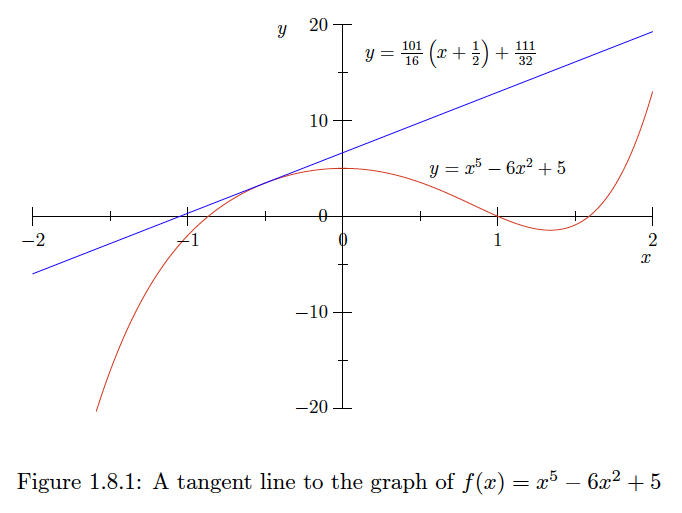

$Screen Shot 2019-11-15 a las 10.50.21 PM.png$

Ejercicio$\PageIndex{1}$

Encuentra una ecuación para la línea tangente a la gráfica de

\[f(x)=3 x^{4}-6 x+3\]en$x=2$.

Contestar: $y=90(x-2)+39$

Ejercicio$\PageIndex{2}$

Encuentra una ecuación para la línea tangente a la gráfica de

\[y=3 \sin ^{2}(x)\]en$x=\frac{\pi}{4}$.

Contestar: $y=3\left(t-\frac{\pi}{4}\right)+\frac{3}{2}$