1.10: Optimización

Los problemas de optimización, es decir, problemas en los que buscamos encontrar el mayor o menor valor de alguna cantidad, son comunes en las aplicaciones de las matemáticas. Debido a la propiedad de valor extremo, existe un algoritmo sencillo para resolver problemas de optimización que involucran funciones continuas en intervalos cerrados y delimitados. De ahí que trataremos este caso primero antes de considerar funciones en otros intervalos.

Recordemos que si\(f(c)\) es el valor máximo, o mínimo, de\(f\) en algún intervalo\(I\) y\(f\) es diferenciable en\(c,\) entonces\(f^{\prime}(c)=0 .\) Consecuentemente, los puntos en los que la derivada se desvanezca jugarán un papel importante en nuestro trabajo de optimización.

Optimización en un Intervalo Cerrado

Supongamos que\(f\) es una función continua en un intervalo cerrado y acotado\([a, b] .\) Por la propiedad de valor extremo,\(f\) alcanza un máximo, así como un valor mínimo, on\([a, b] .\) En particular, hay un número real\(c\) en\([a, b]\) tal que\(f(c) \geq f(x)\) para todos\(x\) en \([a, b] .\)Si\(c\) en\((a, b)\) y\(f\) es diferenciable en\(c,\) entonces debemos tener\(f^{\prime}(c)=0 .\) Las únicas otras posibilidades son que no\(f\) es diferenciable en\(c, c=a,\) o comentarios\(c=b .\) similares se mantienen para los puntos en los que se produce un valor mínimo.

Definición: puntos singulares

Llamamos a un número real\(c\) un punto singular de una función\(f\) si\(f\) se define en un intervalo abierto que contiene\(c,\) pero no es diferenciable en\(c .\)

Teorema\(\PageIndex{1}\)

Si\(f\) es una función continua en un intervalo cerrado y delimitado\([a, b],\), entonces los valores máximo y mínimo de\(f\) ocurren en cualquiera

1. puntos estacionarios en el intervalo abierto\ ((a, b),
2. punto singular en el intervalo abierto\((a, b),\) o (3) los puntos finales de\([a, b] .\)

De ahí que tengamos el siguiente procedimiento para optimizar una función continua\(f\) en un intervalo\([a, b]:\)

1. Encuentra todos los puntos estacionarios y singulares de\(f\) en el intervalo abierto\((a, b)\).
2. Evaluar\(f\) en todos los puntos estacionarios y singulares de\((a, b),\) y en los puntos finales\(a\) y\(b .\)
3. El valor máximo de\(f\) es el valor más grande encontrado en el paso (2) y el valor mínimo de\(f\) es el valor más pequeño encontrado en el paso\((2) .\)

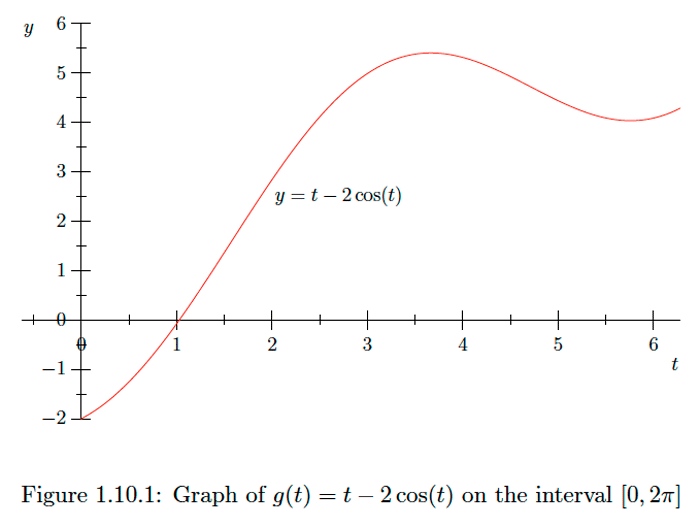
Ejemplo\(\PageIndex{1}\)

Considere la función\(g(t)=t-2 \cos (t)\) definida en el intervalo\([0,2 \pi] .\) Entonces

\[g^{\prime}(t)=1+2 \sin (t) ,\]

y así\(g^{\prime}(t)=0\) cuando

\[\sin (t)=-\frac{1}{2} .\]

Porque\(t\) en el intervalo abierto\((0,2 \pi),\) esto significa que cualquiera

\[t=\frac{7 \pi}{6}\]

o

\[t=\frac{11 \pi}{6} .\]

Es decir, los puntos estacionarios de\(g\) in\((0,2 \pi)\) son\(\frac{7 \pi}{6}\) y\(\frac{11 \pi}{6}\). Tenga en cuenta que\(g\) es diferenciable en todos los puntos en\((0,2 \pi),\) y así no hay puntos singulares de\(g\) en\((0,2 \pi) .\) Por lo tanto, para identificar los valores extremos de\(g\) necesitamos evaluar solo

\[g(0)=-2 ,\]

\[\begin{aligned} g\left(\frac{7 \pi}{6}\right) &=\frac{7 \pi}{6}+\sqrt{3} \approx 5.39724, \\ g\left(\frac{11 \pi}{6}\right) &=\frac{11 \pi}{6}-\sqrt{3} \approx 4.02753, \end{aligned}\]

y

\[g(2 \pi)=2 \pi-2 \approx 4.28319 .\]

Así\(g\) tiene un valor máximo de 5.39724 at\(t=\frac{7 \pi}{6}\) y un valor mínimo de\(-2\) at\(t=0 .\) Ver Figura 1.10 .1 para la gráfica de\(g\) on\([0,2 \pi] .\)

Ejercicio\(\PageIndex{1}\)

Encuentra los valores máximos y mínimos de

\[f(x)=x^{2}+\frac{16}{x}\]

en el intervalo\([1,4]\).

Contestar

Valor máximo de 20 al valor\(x=4 ;\) mínimo de 12 en\(x=2\)

Ejercicio\(\PageIndex{2}\)

Encuentra los valores máximo y mínimo de\(g(t)=t-\sin (2 t)\) en el intervalo\([0, \pi]\).

Contestar

Valor máximo de 3.4840 al valor\(t=\frac{5 \pi}{6} ;\) mínimo de\(-0.3424\) at\(t=\frac{\pi}{6}\)

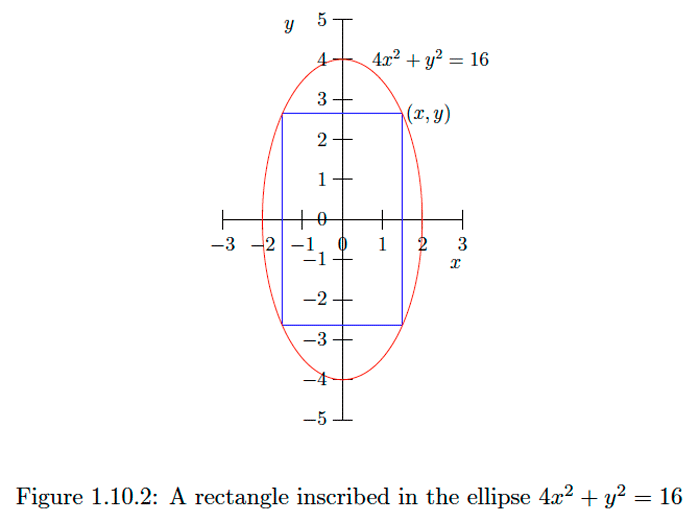
Ejemplo\(\PageIndex{2}\)

Supongamos que inscribimos un rectángulo\(R\) dentro de la elipse\(E\) con ecuación

\[4 x^{2}+y^{2}=16,\]

como se muestra en la Figura\(1.10 .2 .\) Si dejamos\((x, y)\) ser las coordenadas de la esquina superior derecha de\(R,\) entonces el área de\(R\) es

\[A=(2 x)(2 y)=4 x y.\]

ya que\((x, y)\) es un punto en la mitad superior de la elipse, tenemos

\[y=\sqrt{16-4 x^{2}}=2 \sqrt{4-x^{2}},\]

y así

\[A=8 x \sqrt{4-x^{2}}.\]

Ahora supongamos que deseamos encontrar las dimensiones de las\(R\) cuales maximicen su área. Es decir, queremos encontrar el valor máximo de\(A\) en el intervalo\([0,2] .\) Ahora

\[\frac{d A}{d x}=8 x \cdot \frac{-2 x}{2 \sqrt{4-x^{2}}}+8 \sqrt{4-x^{2}}=\frac{-8 x^{2}+8\left(4-x^{2}\right)}{\sqrt{4-x^{2}}}=\frac{32-16 x^{2}}{\sqrt{4-x^{2}}} .\]

De ahí\(\frac{d A}{d x}=0,\) para\(x\) en\((0,2),\) cuando\(32-16 x^{2}=0,\) eso es, cuando\(x=\sqrt{2} .\) Así el valor máximo de\(A\) debe ocurrir en\(x=0, x=\sqrt{2},\) o\(x=2 .\) Evaluando, tenemos

\[\left.A\right|_{x=0}=0,\]

\[\left.A\right|_{x=\sqrt{2}}=8 \sqrt{2} \sqrt{2}=16,\]

y

\[\left.A\right|_{x=2}=0.\]

De ahí que el rectángulo\(R\) inscrito en\(E\) con el área más grande tenga área 16 cuando\(x=\sqrt{2}\) y es\(y=2 \sqrt{2} .\) decir,\(R\) es\(2 \sqrt{2}\) por\(4 \sqrt{2}\).

Ejercicio\(\PageIndex{3}\)

Encuentra las dimensiones del rectángulo\(R\) con mayor área que puede ser inscrita en la elipse con ecuación

\[\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1,\]

donde\(a\) y\(b\) son números reales positivos.

Contestar

\(R\)es\(\sqrt{2} a\) por\(\sqrt{2} b\)

Ejercicio\(\PageIndex{4}\)

Un trozo de alambre, de 100 centímetros de longitud, se corta en dos trozos, uno de los cuales se utiliza para formar un cuadrado y el otro un círculo. Encuentra las longitudes de las piezas para que la suma de las áreas del cuadrado y el círculo sean (a) máxima y (b) mínima.

Contestar

(a) todo el alambre se utiliza para el círculo;

(b) 43.99 cm de uso para el cuadrado,\(56.01 \mathrm{cm}\) utilizado para el círculo

Ejercicio\(\PageIndex{5}\)

Mostrar que de todos los rectángulos de un perímetro dado\(P,\) el cuadrado es el que tiene el área más grande

Optimización en otros intervalos

Consideramos ahora el caso de una función continua\(f\) en un intervalo\(I\) que o bien no está cerrado o no acotado. La propiedad de valor extremo no aplica en este caso, y, como hemos visto, no tenemos ninguna garantía de que\(f\) tenga un valor extremo en el intervalo. De ahí que, en general, esta situación requiera un análisis más cuidadoso que el del apartado anterior.

Sin embargo, hay un caso que surge con frecuencia y que es capaz de un simple análisis. Supongamos que\(c\) es un punto en el\(I\) que es un punto estacionario o singular de\(f,\) y que\(f\) es diferenciable en todos los demás puntos de\(I\). Si\(f^{\prime}(x)<0\) para todos\(x\) en\(I\) con\(x<c\) y\(f^{\prime}(x)>0\) para todos\(x\) en\(I\) con\(c<x,\) entonces\(f\) está disminuyendo antes\(c\) y aumentando después\(c,\) y así debe tener un valor mínimo en\(c .\) Similarmente, si\(f^{\prime}(x)>0\) para todos \(x\)in\(I\) with\(x<c\) and\(f^{\prime}(x)<0\) for all\(x\) in\(I\) with\(c<x,\) then\(f\) is increasing before\(c\) and decrece after\(c,\) and so must have a maximum value at\(c .\) Los siguientes ejemplos ilustrarán.

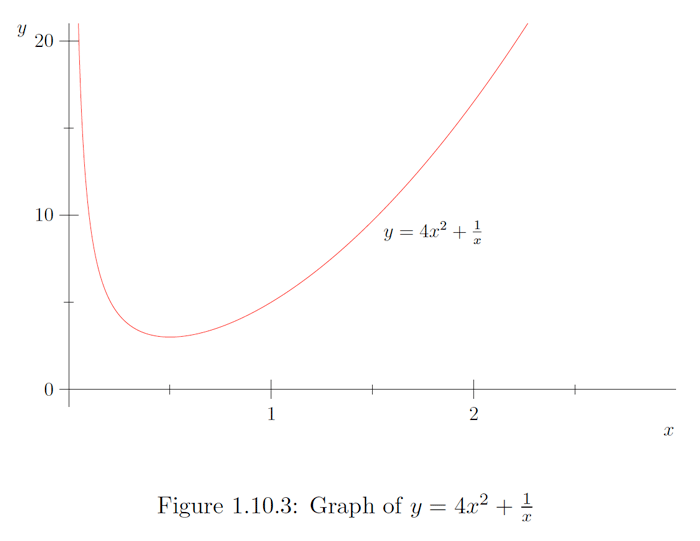
Ejemplo\(\PageIndex{3}\)

Considerar el problema de encontrar los valores extremos de

\[ y=4 x^{2}+\frac{1}{x} \]

en el intervalo\((0, \infty) .\) Desde

\[\frac{d y}{d x}=8 x-\frac{1}{x^{2}} ,\]

vemos que\(\frac{d y}{d x}<0\) cuando, y sólo cuando,

\[8 x<\frac{1}{x^{2}} .\]

Esto es equivalente a

\[x^{3}<\frac{1}{8} ,\]

así\(\frac{d y}{d x}<0\) sucesivamente\((0, \infty)\) cuando, y solo cuando,\(0<x<\frac{1}{2} .\) Del mismo modo, vemos que\(\frac{d y}{d x}>0\) cuando, y solo cuando,\(x>\frac{1}{2} .\) Así\(y\) es una función decreciente de\(x\) sobre el intervalo\(\left(0, \frac{1}{2}\right)\) y una función creciente de\(x\) en el intervalo\(\left(\frac{1}{2}, \infty\right),\) y así debe tener un mínimo valor en\(x=\frac{1}{2} .\) Nota, sin embargo, que\(y\) no tiene un valor máximo: dado cualquiera\(x=c,\) si\(c<\frac{1}{2}\) podemos encontrar un valor mayor para\(y\) usando cualquiera\(0<x<c,\) y si\(c>\frac{1}{2}\) podemos encontrar un valor mayor para\(y\) mediante el uso de cualquier\(x>c .\) Así concluimos que \(y\)tiene un valor mínimo de 3 at\(x=\frac{1}{2},\) pero no tiene un valor máximo. Ver Figura\(1.10 .3 .\)

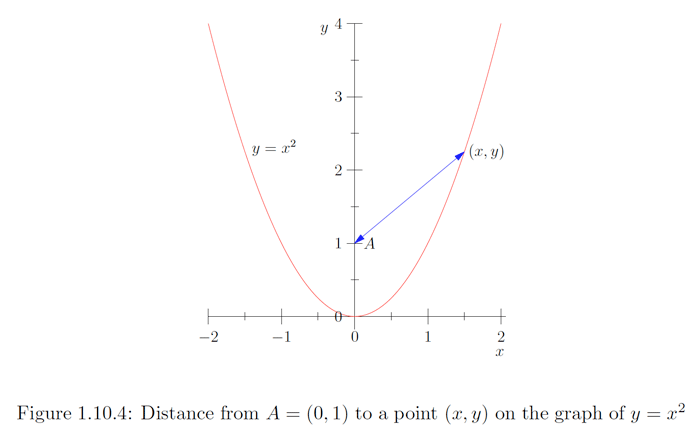
Ejemplo\(\PageIndex{4}\)

Considera el problema de encontrar la distancia más corta del punto\(A=(0,1)\) a la parábola\(P\) con ecuación\(y=x^{2} .\) Si\((x, y)\) es un punto encendido\(P (\text { see Figure } 1.10 .4),\) entonces la distancia de\(A\) a\((x, y)\) es

\[D=\sqrt{(x-0)^{2}+(y-1)^{2}}=\sqrt{x^{2}+\left(x^{2}-1\right)^{2}} .\]

Nuestro problema entonces es encontrar el valor mínimo de\(D\) en el intervalo\((-\infty, \infty) .\) Sin embargo, para que el problema sea algo más fácil de trabajar, observamos que, dado que siempre\(D\) es un valor positivo, encontrar el valor mínimo de\(D\) es equivalente

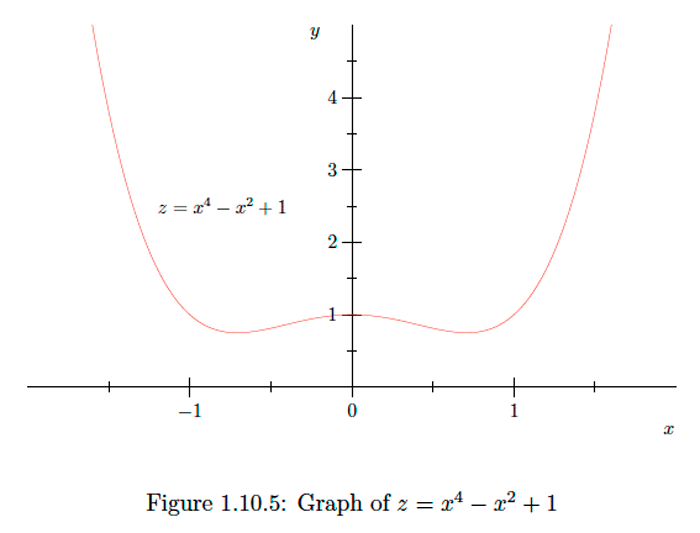
a encontrar el valor mínimo de\(D^{2} .\) Así que dejar

\[z=D^{2}=x^{2}+\left(x^{2}-1\right)^{2}=x^{2}+x^{4}-2 x^{2}+1=x^{4}-x^{2}+1 ,\]

nuestro problema se convierte en el de encontrar el valor mínimo de\(z\) on\((-\infty, \infty) .\) Now

\[\frac{d z}{d x}=4 x^{3}-2 x ,\]

así\(\frac{d z}{d x}=0\) cuando, y sólo cuando,

\[0=4 x^{3}-2 x=2 x\left(2 x^{2}-1\right) ,\]

es decir, cuando, y solo cuando,\(x=-\frac{1}{\sqrt{2}}, x=0,\) o\(x=\frac{1}{\sqrt{2}} .\) Ahora\(2 x<0\) cuando\(-\infty<x<0\) y\(2 x>0\) cuando\(0<x<\infty,\) mientras que\(2 x^{2}-1<0\) cuando\(-\frac{1}{\sqrt{2}}<x<\frac{1}{\sqrt{2}}\) y\(2 x^{2}-1>0\) ya sea cuando\(x<-\frac{1}{\sqrt{2}}\) o cuando\(x>\frac{1}{\sqrt{2}} .\) Tomando el producto de\(2 x\) y\(2 x^{2}-1,\) vemos que\(\frac{d z}{d x}<0\) cuando \(x<-\frac{1}{\sqrt{2}}\)y cuándo\(0<x<\frac{1}{\sqrt{2}},\) y\(\frac{d z}{d x}>0\) cuándo\(-\frac{1}{\sqrt{2}}<x<0\) y cuándo\(x>\frac{1}{\sqrt{2}} .\) Se deduce que\(z\) es una función decreciente de\(x\)\(\left(-\infty,-\frac{1}{\sqrt{2}}\right)\) encendido\(\left(0, \frac{1}{\sqrt{2}}\right),\) y encendido y es una función creciente de\(x\) encendido\(\left(-\frac{1}{\sqrt{2}}, 0\right)\) y encendido\(\left(\frac{1}{\sqrt{2}}, \infty\right)\).

Ahora se deduce que\(z\) tiene un mínimo local de\(\frac{3}{4}\) a\(x=-\frac{1}{\sqrt{2}},\) un máximo local de 1 en\(x=0,\) y otro mínimo local de\(\frac{3}{4}\) en\(x=\frac{1}{\sqrt{2}} .\) Nota que\(\frac{3}{4}\) es el valor mínimo\(z\) tanto en el intervalo\((-\infty, 0)\) como en el intervalo\((0, \infty) ;\) desde \(z\)tiene un máximo local de 1 en\(x=0,\) ello se deduce que\(\frac{3}{4}\) es de hecho el valor mínimo de\(z\) on\((-\infty, \infty) .\) Por lo tanto, podemos concluir que la distancia mínima de\(A\) a\(P\) es\(\frac{\sqrt{3}}{2},\) y los puntos\(P\) más cercanos a\(A\) son\(\left(-\frac{1}{\sqrt{2}}, \frac{1}{2}\right)\) y\(\left(\frac{1}{\sqrt{2}}, \frac{1}{2}\right) .\) Tenga en cuenta, sin embargo, que\(z\) no tiene un valor máximo, a pesar de que tiene un valor máximo local en\(x=0 .\) Ver Figura 1.10 .5 para la gráfica de\(z\).

Ejercicio\(\PageIndex{6}\)

Encuentra el punto en la parábola\(y=x^{2}\) que está más cerca del punto\((3,0)\).

Contestar

\((1,1)\)

Ejercicio\(\PageIndex{7}\)

Mostrar que de todos los rectángulos de un área dada\(A,\) el cuadrado es el que tiene el perímetro más corto.

Ejercicio\(\PageIndex{8}\)

Mostrar que de todos los cilindros circulares correctos con un volumen fijo\(V,\) el de altura y diámetro iguales tiene la superficie mínima.

Ejercicio\(\PageIndex{9}\)

Encuentra los puntos en la elipse\(4 x^{2}+y^{2}=16\) que están\((a)\) más cerca y (b) más alejados del punto\((0,1)\).

Contestar

a)\(\left(\frac{4 \sqrt{2}}{3}, \frac{4}{3}\right)\)\(\left(-\frac{4 \sqrt{2}}{3}, \frac{4}{3}\right)\) yb)\((0,-4)\)