1.12: Derivados de orden superior

Dadas dos cantidades,\(y\) y\(x,\) con\(y\) una función de\(x,\) sabemos que la derivada\(\frac{d y}{d x}\) es la tasa de cambio de\(y\) con respecto a\(x\). Ya que\(\frac{d y}{d x}\) es entonces en sí misma una función de\(x,\) podemos pedir su tasa de cambio con respecto a la\(x,\) cual denominamos la derivada de segundo orden de\(y\) con respecto a\(x\) y denotar\(\frac{d^{2} y}{d x^{2}} .\)

Ejemplo\(\PageIndex{1}\)

Si\(y=4 x^{5}-3 x^{2}+4,\) entonces

\[\frac{d y}{d x}=20 x^{4}-6 x ,\] y así Por \[\frac{d^{2} y}{d x^{2}}=80 x^{3}-6 .\] supuesto, podríamos seguir diferenciando: la tercera derivada de\(y\) con respecto a\(x\) es \[\frac{d^{3} y}{d x^{3}}=240 x^{2} ,\] la cuarta derivada de\(y\) con respecto a\(x\) es \[\frac{d^{4} y}{d x^{4}}=480 x ,\] y así sucesivamente.

Si\(y\) es una función de\(x\) con\(y=f(x),\) entonces también podemos denotar la segunda derivada de\(y\) con respecto a\(x\) por\(f^{\prime \prime}(x),\) la tercera derivada por\(f^{\prime \prime \prime}(x),\) y así sucesivamente. La notación prima se vuelve engorrosa después de un tiempo, y así podemos reemplazar los primos con el número correspondiente entre paréntesis; es decir, podemos escribir, por ejemplo,\(f^{\prime \prime \prime \prime}(x)\) como\(f^{(4)}(x)\).

Ejemplo\(\PageIndex{2}\)

Si

\[f(x)=\frac{1}{x} ,\] entonces \[\begin{aligned} f^{\prime}(x) &=-\frac{1}{x^{2}}, \\[12pt] f^{\prime \prime}(x) &=\frac{2}{x^{3}}, \\[12pt] f^{\prime \prime \prime}(x) &=-\frac{6}{x^{4}}, \end{aligned}\] y \[f^{(4)}(x)=\frac{24}{x^{5}} .\]

Ejercicio\(\PageIndex{1}\)

Encuentra el primero, segundo, y derivados de tercer orden de\(y=\sin (2 x)\).

Contestar

\(\frac{d y}{d x}=2 \cos (2 x), \frac{d^{2} y}{d x^{2}}=-4 \sin (2 x), \frac{d^{3} y}{d x^{3}}=-8 \cos (2 x)\)

Ejercicio\(\PageIndex{2}\)

Encuentra el primero, segundo, y derivados de tercer orden de\(f(x)=\sqrt{4 x+1}\).

Contestar

\(f^{\prime}(x)=\frac{2}{\sqrt{4 x+1}}, f^{\prime \prime}(x)=-\frac{4}{(4 x+1)^{\frac{3}{2}}}, f^{\prime \prime \prime}(x)=\frac{6}{(4 x+1)^{\frac{5}{2}}}\)

Aceleración

Si\(x\) es la posición, en el momento\(t,\) de que un objeto se mueve a lo largo de una línea recta, entonces sabemos que

\[v=\frac{d x}{d t}\] es la velocidad del objeto en el momento\(t .\) ya que la aceleración es la velocidad de cambio de velocidad, se deduce que la aceleración del objeto es \[a=\frac{d v}{d t}=\frac{d^{2} x}{d t^{2}} .\]

Ejemplo\(\PageIndex{3}\)

Supongamos que un objeto, como una bola de plomo, se deja caer desde una altura de 100 metros. Ignorando la resistencia del aire, la altura de la bola sobre la tierra después de\(t\) segundos viene dada por

\[x(t)=100-4.9 t^{2} \text { meters, }\] como lo discutimos en la Sección 1.2. De ahí que la velocidad del objeto después de\(t\) segundos sea \[v(t)=-9.8 t \text { meters / second }\] y la aceleración del objeto es \[a(t)=-9.8 \text { meters / second }^{2}.\] Así la aceleración de un objeto en caída libre cerca de la superficie de la tierra, ignorando la resistencia del aire, es constante. Históricamente, Galileo comenzó con esta observación sobre la aceleración de los ojetes en caída libre y trabajó en la otra dirección para descubrir las fórmulas de velocidad y posición.

Ejercicio\(\PageIndex{3}\)

Supongamos que un objeto que oscila al final de un resorte tiene posición\(x=10 \cos (\pi t)\) (medida en centímetros desde la posición de equilibrio) en el tiempo\(t\) segundos. Encuentra la aceleración del objeto en el momento\(t=1.25 .\)

Contestar

\(69.79 \mathrm{cm} / \mathrm{sec}\)

Concavidad

La segunda derivada de una función nos\(f\) dice la velocidad a la que\(f\) está cambiando la pendiente de la gráfica de. Geométricamente, esto se traduce en medir la concavidad de la gráfica de la función.

Definición

Decimos que la gráfica de una función\(f\) es cóncava hacia arriba en un intervalo abierto\((a, b)\) si\(f^{\prime}\) es una función creciente en\((a, b) .\) Decimos que la gráfica de una función\(f\) es cóncava hacia abajo en un intervalo abierto\((a, b)\) si\(f^{\prime}\) es una función decreciente en\((a, b) .\)

Para determinar la concavidad de la gráfica de una función\(f,\) necesitamos determinar los intervalos en los que\(f^{\prime}\) está aumentando y los intervalos en los que\(f^{\prime}\) va disminuyendo. De ahí que a partir de nuestro trabajo anterior, necesitamos identificar cuándo la derivada de\(f^{\prime}\) es positiva y cuándo es negativa.

Teorema\(\PageIndex{1}\)

Si\(f\) es dos veces diferenciable en\((a, b),\) entonces la gráfica de\(f\) es cóncava hacia arriba en\((a, b)\) si\(f^{\prime \prime}(x)>0\) para todos\(x\) en\((a, b),\) y cóncava hacia abajo en\((a, b)\) si\(f^{\prime \prime}(x)<0\) para todos\(x\) en\((a, b) .\)

Ejemplo\(\PageIndex{4}\)

Si\(f(x)=2 x^{3}-3 x^{2}-12 x+1,\) entonces

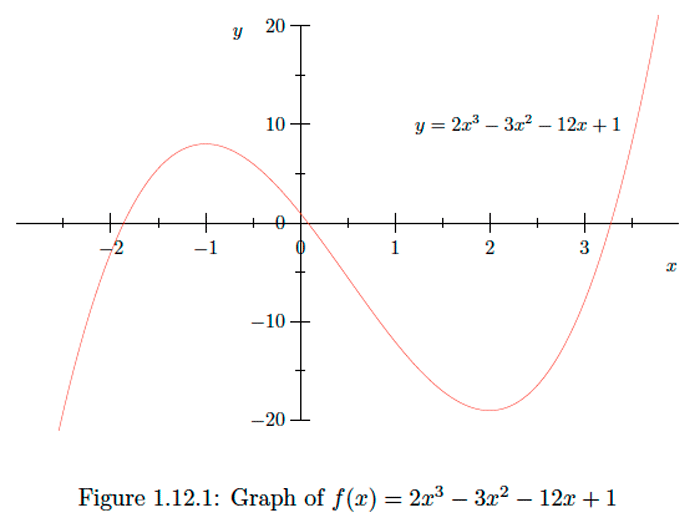
\[f^{\prime}(x)=6 x^{2}-6 x-12\] y \[f^{\prime \prime}(x)=12 x-6 .\] De ahí\(f^{\prime \prime}(x)<0\) cuándo\(x<\frac{1}{2}\) y\(f^{\prime \prime}(x)>0\) cuándo\(x>\frac{1}{2},\) y así la gráfica de\(f\) es cóncava hacia abajo en el intervalo\(\left(-\infty, \frac{1}{2}\right)\) y cóncava hacia arriba en el intervalo\(\left(\frac{1}{2}, \infty\right) .\) Se puede ver la distinción entre cóncava hacia abajo y cóncava hacia arriba muy claramente en la gráfica de que\(f\) se muestra en la Figura\(1.12 .1 .\) Llamamos a un punto en la gráfica de una función\(f\) en la que la concavidad cambia, ya sea de arriba a abajo o de abajo a arriba, un punto de inflexión. En el ejemplo anterior,\(\left(\frac{1}{2},-\frac{11}{2}\right)\) es un punto de inflexión.

Ejercicio\(\PageIndex{4}\)

Encuentra los intervalos en los que la gráfica\(f(x)=5 x^{3}-3 x^{5}\) es cóncava hacia arriba y los intervalos en los que la gráfica es cóncava hacia abajo. ¿Cuáles son los puntos de inflexión?

Contestar

Cóncavo hacia arriba\((-\infty,-1)\) y\((0,1) ;\) cóncavo hacia abajo\((-1,0)\) y\((1, \infty) ;\) Puntos de inflexión:\((-1,-2),(0,0),(1,2)\)

La prueba de la segunda derivada

Supongamos que\(c\) es un punto estacionario de\(f\) y\(f^{\prime \prime}(c)>0 .\) Entonces, ya que\(f^{\prime \prime}\) es el derivado de\(f^{\prime}\) y\(f^{\prime}(c)=0,\) para cualquier infinitesimal\(d x \neq 0\),

\[\frac{f^{\prime}(c+d x)-f^{\prime}(c)}{d x}=\frac{f^{\prime}(c+d x)}{d x}>0 .\] De ello se deduce que\(f^{\prime}(c+d x)>0\) cuándo\(d x>0\) y\(f^{\prime}(c+d x)<0\) cuándo\(d x<0\). De ahí\(f\) está disminuyendo a la izquierda de\(c\) y aumentando a la derecha de\(c,\) y así\(f\) tiene un mínimo local en\(c .\) Similarmente, si\(f^{\prime \prime}(c)<0\) en un punto estacionario\(c,\) entonces\(f\) tiene un máximo local en\(c .\) Este resultado es la prueba de la segunda derivada .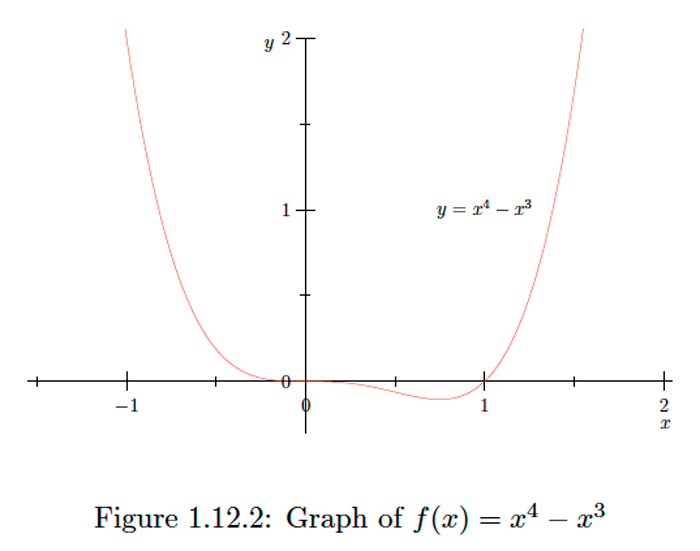

Ejemplo\(\PageIndex{5}\)

Si\(f(x)=x^{4}-x^{3},\) entonces

\[f^{\prime}(x)=4 x^{3}-3 x^{2}=x^{2}(4 x-3)\] y \[f^{\prime \prime}(x)=12 x^{2}-6 x=6 x(2 x-1) .\] De ahí\(f\) tiene puntos estacionarios\(x=0\) \[f^{\prime \prime}(0)=0\] y\(x=\frac{3}{4} .\) Desde y \[f^{\prime \prime}\left(\frac{3}{4}\right)=\frac{9}{4}>0 ,\] vemos que\(f\) tiene un mínimo local a\(x=\frac{3}{4} .\) Aunque la segunda prueba derivada no nos dice nada sobre la naturaleza del punto crítico \(x=0,\)sabemos, ya que\(f\) tiene un mínimo local en\(x=\frac{3}{4},\) que\(f\) está disminuyendo sobre\(\left(0, \frac{3}{4}\right)\) y aumentando en\(\left(\frac{3}{4}, \infty\right) .\) Además, ya que\(4 x-3<0\) para todos\(x<0,\) se deduce que\(f^{\prime}(x)<0\) para todos\(x<0,\) y así también\(f\) está disminuyendo en\((-\infty, 0) .\) De ahí\(f\) que no tenga ni un máximo local ni un mínimo local en\(x=0 .\) Finalmente, ya que\(f^{\prime \prime}(x)<0\) para\(0<x<\frac{1}{2}\) y\(f^{\prime \prime}(x)>0\) para todos los demás\(x,\) vemos que la gráfica de\(f\) es cóncava hacia abajo en el intervalo\(\left(0, \frac{1}{2}\right)\) y cóncava hacia arriba en los intervalos\((-\infty, 0)\) y \(\left(\frac{1}{2}, \infty\right)\). Ver Figura\(1.12 .2 .\)

Ejercicio\(\PageIndex{5}\)

Utilice la prueba de la segunda derivada para encontrar todos los máximos y mínimos locales de

\[f(x)=x+\frac{1}{x} .\]

Contestar

Máximo local de\(-2\) al mínimo\(x=-1 ;\) local de 2 en\(x=1\)

Ejercicio\(\PageIndex{6}\)

Encuentra todos los máximos y mínimos locales de\(g(t)=5 t^{7}-7 t^{5}\).

Contestar

Máximo local de 2 al mínimo\(t=-1 ;\) local de\(-2\) al\(t=1\)