3.2: El teorema del valor medio

Última actualización
Guardar como PDF

Page ID: 111782

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Motivamos esta sección con la siguiente pregunta: Supongamos que sale de su casa y conduce a la casa de su amigo en una ciudad a 100 millas de distancia, completando el viaje en dos horas. ¿En algún momento del viaje necesariamente tienes que ir a 50 millas por hora?

Al responder a esta pregunta, es claro que la velocidad promedio para todo el viaje es de 50 mph (es decir, 100 millas en 2 horas), pero la pregunta es si su velocidad instantánea es o no exactamente de 50 mph. Más simple, ¿tu velocímetro alguna vez lee exactamente 50 mph?. La respuesta, bajo algunos supuestos muy razonables, es “sí"'

Veamos ahora por qué esta situación está en un texto de cálculo traduciéndolo en símbolos matemáticos.

Primero asume que la función$y = f(t)$ da la distancia (en millas) recorrida desde tu casa en el momento$t$ (en horas) donde$0\le t\le 2$. En particular, esto da$f(0)=0$ y$f(2)=100$. La pendiente de la línea secante que conecta los puntos$(0,f(0))$ inicial y final y, por lo tanto,$(2,f(2))$ es

$$
\ frac {\ Delta f} {\ Delta t} =\ frac {f (2) -f (0)} {2-0} =\ frac {100-0} {2} = 50\,\ text {mph}.
\]

La pendiente en cualquier punto de la propia gráfica viene dada por la derivada$f'(t)$. Entonces, dado que la respuesta a la pregunta anterior es “sí”, esto significa que en algún momento durante el viaje, la derivada adquiere el valor de 50 mph. Simbólicamente,

$$
f' (c) =\ frac {f (2) -f (0)} {2-0} = 50
\]

por algún tiempo$0\le c \le 2.$

¿Qué tal de manera más general? Dada alguna función$y=f(x)$ y un rango$a\le x\le b$ hace el valor de la derivada en algún punto entre$a$ y$b$ tiene que coincidir con la pendiente de la línea secante que conecta los puntos$(a,f(a))$ y$(b,f(b))$? O equivalentemente, ¿la ecuación

\[f'(c) = \frac{f(b)-f(a)}{b-a}\]

tiene que aguantar para algunos$a < c < b$?

Veamos dos funciones en un ejemplo.

Ejemplo$\PageIndex{1}$: Comparing average and instantaneous rates of change

Considerar funciones

$$f_1 (x) =\ frac {1} {x^2}\ quad\ texto {y}\ quad f_2 (x) = |x|\]

con$a=-1$ y$b=1$ como se muestra en la Figura$\PageIndex{1}$ (a) y (b), respectivamente. Ambas funciones tienen un valor de 1 at$a$ y$b$. Por lo tanto, la pendiente de la línea secante que conecta los puntos finales es$0$ en cada caso. Pero si miras las parcelas de cada una, puedes ver que no hay puntos en ninguna de las gráficas donde las líneas tangentes tengan pendiente cero. Por lo tanto hemos encontrado que no hay$c$ en$[-1,1]$ tal que

$$f' (c) =\ frac {f (1) -f (-1)} {1- (-1)} = 0.\]

$alt$ $alt$

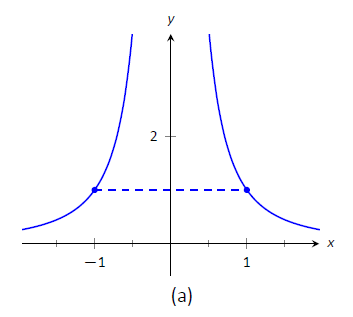
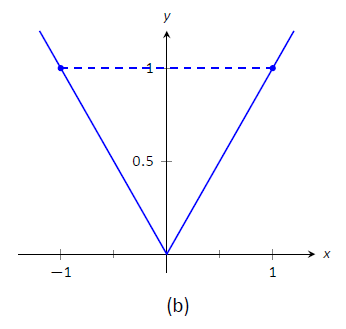
Figura$\PageIndex{1}$: Una gráfica de$f_1(x) = 1/x^2$ y$f_2(x) = |x|$ en Ejemplo$\PageIndex{1}$.

Entonces, ¿qué salió “mal"'? Puede que no sea sorprendente encontrar que la discontinuidad de$f_1$ y la esquina de$f_2$ jugar un papel. Si nuestras funciones hubieran sido continuas y diferenciables, ¿hubiéramos podido encontrar ese valor especial$c$? Esta es nuestra motivación para el siguiente teorema.

Teorema$\PageIndex{1}$: The Mean Value Theorem of Differentiation

Dejar$y=f(x)$ ser función continua en el intervalo cerrado$[a,b]$ y diferenciable en el intervalo abierto$(a,b)$. Existe un valor$c$,$a < c < b$, tal que
$$
f' (c) =\ frac {f (b) -f (a)} {b-a}.
$$ Es
decir, hay un valor$c$ en$(a,b)$ donde la tasa instantánea de cambio de$f$ at$c$ es igual a la tasa promedio de cambio de$f$ on$[a,b]$.

Obsérvese que las razones por las que$\PageIndex{1}$ fallan las funciones en Ejemplo son efectivamente que$f_1$ tiene una discontinuidad en el intervalo$[-1,1]$ y no$f_2$ es diferenciable en el origen.

Daremos una prueba del Teorema del Valor Medio a continuación. Para ello, utilizamos un hecho, llamado Teorema de Rolle, que aquí se afirma.

Teorema$\PageIndex{2}$: Rolle's Theorem

Dejar$f$ ser continuo$[a,b]$ y diferenciable en$(a,b)$, donde$f(a) = f(b)$. Hay algunos$c$ en$(a,b)$ tal que$f'(c) = 0.$

Considere Figura$\PageIndex{2}$ donde se da la gráfica de$f$ una función, donde$f(a) = f(b)$. Debe tener sentido intuitivo que si$f$ es diferenciable (y por lo tanto, continuo) que habría un valor$c$ en$(a,b)$ donde$f'(c)=0$; es decir, habría un máximo o mínimo relativo de$f$ in$(a,b)$. El Teorema de Rolle garantiza al menos uno; puede haber más.

$alt$

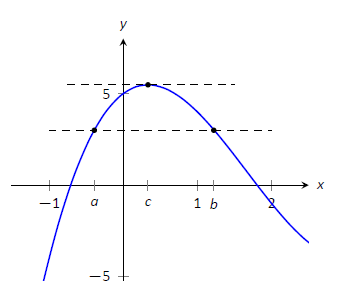
FIGURA$\PageIndex{2}$: Una gráfica de$f(x) = x^3-5x^2+3x+5$, donde$f(a) = f(b)$. Obsérvese la existencia de$c$, dónde$a<c<b$, dónde$f'(c)=0$.

El Teorema de Rolle es realmente solo un caso especial del Teorema del Valor Medio. Si$f(a) = f(b)$, entonces la tasa promedio de cambio en$(a,b)$ es$0$, y el teorema garantiza$c$ en alguna parte$f'(c)=0$. Demostraremos el Teorema de Rolle, luego lo usaremos para probar el Teorema del Valor Medio.

Prueba del teorema de Rolle

Dejar$f$ ser diferenciable en$(a,b)$ donde$f(a)=f(b)$. Consideramos dos casos.

Caso 1: Considerar el caso cuando$f$ es constante encendido$[a,b]$; es decir,$f(x) = f(a) = f(b)$ para todos$x$ en$[a,b]$. Entonces$f'(x) = 0$ para todos$x$ adentro$[a,b]$, mostrando que hay al menos un valor$c$ en$(a,b)$ donde$f'(c)=0$.

Caso 2: Ahora supongamos que no$f$ es constante en$[a,b]$. El Teorema del Valor Extremo garantiza que$f$ tiene un valor máximo y mínimo on$[a,b]$, encontrado ya sea en los puntos finales o en un valor crítico en$(a,b)$. Dado que$f(a)=f(b)$ y no$f$ es constante, es evidente que el máximo y el mínimo no se pueden encontrar ambos en los puntos finales. Asumir, sin pérdida de generalidad, que el máximo de no$f$ se encuentra en los puntos finales. Por lo tanto hay una$c$ en$(a,b)$ tal que$f(c)$ es el valor máximo de$f$. Por Teorema 3.1.2,$c$ debe ser un número crítico de$f$; ya que$f$ es diferenciable, tenemos eso$f'(c) = 0$, completando la prueba del teorema.

$\square$

Ahora podemos probar el Teorema del Valor Medio.

Prueba del Teorema del Valor Medio

Definir la función

$$g (x) = f (x) -\ frac {f (b) -f (a)} {b-a} x.\]

Sabemos que$g$ es diferenciable en$(a,b)$ y continuo en$[a,b]$ ya que$f$ es. Podemos mostrar$g(a)=g(b)$ (en realidad es más fácil de mostrar$g(b)-g(a)=0$, lo cual es suficiente). Entonces podemos aplicar el teorema de Rolle para garantizar la existencia de$c \in (a,b)$ tal que$g'(c) = 0$. Pero tenga en cuenta que

$0= g' (c) = f' (c) -\ frac {f (b) -f (a)} {b-a}\;\]

de ahí

$$f' (c) =\ frac {f (b) -f (a)} {b-a},\]

que es lo que buscábamos probar.

$\square$

Volviendo al comienzo mismo de la sección, vemos que la única suposición que necesitaríamos de nuestra función de distancia$f(t)$ es que sea continua y diferenciable$t$ de 0 a 2 horas (ambas suposiciones razonables). Por el Teorema del Valor Medio, se nos garantiza un tiempo durante el viaje donde nuestra velocidad instantánea es de 50 mph. Este hecho se utiliza en la práctica. Algunos organismos encargados de hacer cumplir la ley monitorean las velocidades del tráfico mientras están en No miden la velocidad con radar, sino al cronometrar autos individuales a medida que pasan por encima de líneas pintadas en la carretera cuyas distancias de separación se conocen. El oficial es capaz de medir la velocidad promedio de un automóvil entre las líneas pintadas; si esa velocidad promedio es mayor que el límite de velocidad publicado, el oficial tiene la seguridad de que el conductor superó el límite de velocidad en algún momento.

Nótese que el Teorema del Valor Medio es un teorema de existencia. Afirma que$c$ existe un valor especial, pero no da ninguna indicación sobre cómo encontrarlo. Resulta que cuando necesitamos el Teorema del Valor Medio, la existencia es todo lo que necesitamos

Ejemplo$\PageIndex{2}$: Using the Mean Value Theorem

Considerar$f(x) = x^3+5x+5$ en$[-3,3]$. Encontrar$c$ en$[-3,3]$ que satisfaga el Teorema del Valor Medio.

Solución

La tasa promedio de cambio de$f$ on$[-3,3]$ es:

\[\frac{f(3)-f(-3)}{3-(-3)} = \frac{84}{6} = 14.\]

Queremos encontrar$c$ tal que$f'(c) = 14$. Nos encontramos$f'(x) = 3x^2+5$. Establecemos esto igual a 14 y resolvemos para$x$.

\[ \begin{align*} f'(x) &= 14 \\ 3x^2 +5 &= 14\\ x^2 &= 3\\ x &= \pm \sqrt{3} \approx \pm 1.732 \end{align*}\]

Se han encontrado 2 valores$c$ en$[-3,3]$ donde la tasa instantánea de cambio es igual a la tasa promedio de cambio; el Teorema del Valor Medio garantizó al menos uno. En la Figura$\PageIndex{3}$$f$ se grafica con una línea discontinua que representa la tasa promedio de cambio; también$x=\pm \sqrt{3}$ se dan las líneas tangentes a$f$ at. Observe cómo estas líneas son paralelas (es decir, tienen la misma pendiente) que la línea discontinua.

$alt$

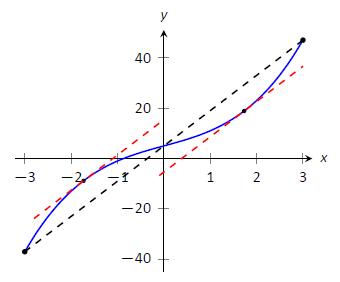
Figura$\PageIndex{3}$: Demostrando el Teorema del Valor Medio en el Ejemplo$\PageIndex{2}$.

Si bien el Teorema del Valor Medio tiene un uso práctico (por ejemplo, la aplicación de monitoreo de velocidad mencionada anteriormente), se usa principalmente para avanzar en otra teoría. Lo usaremos en la siguiente sección para relacionar la forma de una gráfica con su derivada.