3.4: Concavidad y Segunda Derivada

Última actualización
Guardar como PDF

Page ID: 111779

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Nuestro estudio de las funciones “agradables” continúa. En el apartado anterior se mostró cómo la primera derivada de una función,$f'$, puede retransmitirle información importante sobre$f$. Ahora aplicamos la misma técnica a$f'$ sí mismo, y aprendemos de qué nos habla esto$f$. La clave para estudiar$f'$ es considerar su derivada, es decir$f''$, que es la segunda derivada de$f$. Cuando$f''>0$,$f'$ va en aumento. Cuando$f''<0$,$f'$ es decreciente. $f'$tiene máximos y mínimos relativos donde$f''=0$ o es indefinido. Esta sección explora cómo conocer la información sobre$f''$ da información sobre$f$.

Concavidad

Comenzamos con una definición, luego exploramos su significado.

Definición Cóncava arriba y cóncava abajo

Dejar$f$ ser diferenciable en un intervalo$I$. La gráfica de$f$ es cóncava hacia arriba en$I$ si$f'$ va en aumento. La gráfica de$f$ es cóncava hacia abajo en$I$ si$f'$ es decreciente. Si$f'$ es constante entonces$f$ se dice que la gráfica de no tiene concavidad.

Nota: A menudo declaramos que "$f$es cóncavo hacia arriba” en lugar de “la gráfica de$f$ es cóncava hacia arriba” por simplicidad.

La gráfica de una función$f$ es cóncava hacia arriba cuando$f'$ va en aumento. Eso significa que a medida que se mira una gráfica cóncava hacia arriba de izquierda a derecha, las pendientes de las líneas tangentes irán aumentando. Considere Figura$\PageIndex{1}$, donde se muestra una gráfica cóncava hacia arriba junto con algunas líneas tangentes. Observe cómo la línea tangente de la izquierda es empinada, hacia abajo, correspondiente a un pequeño valor de$f'$. A la derecha, la línea tangente es empinada, hacia arriba, correspondiente a un gran valor de$f'$.

$alt$

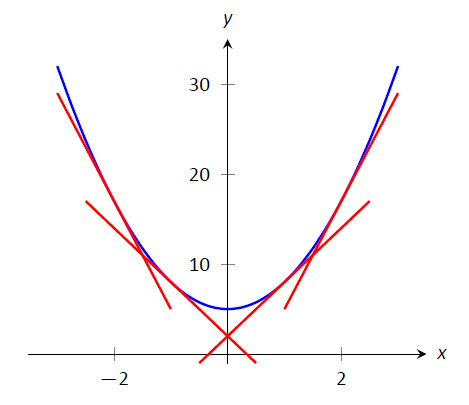
Figura$\PageIndex{1}$: Una función$f$ con una gráfica cóncava hacia arriba. Observe cómo las pendientes de las líneas tangentes, al mirar de izquierda a derecha, van aumentando.

Si una función es decreciente y cóncava hacia arriba, entonces su tasa de disminución se está desacelerando; está “nivelando”. Si la función es creciente y cóncava hacia arriba, entonces la tasa de aumento va en aumento. La función está aumentando a un ritmo cada vez más rápido.

Consideremos ahora una función que es cóncava hacia abajo. Esencialmente repetimos los párrafos anteriores con ligera variación.

La gráfica de una función$f$ es cóncava hacia abajo cuando$f'$ está disminuyendo. Eso significa que a medida que se mira una gráfica cóncava hacia abajo de izquierda a derecha, las pendientes de las líneas tangentes irán disminuyendo. Considere Figura$\PageIndex{2}$, donde se muestra una gráfica cóncava hacia abajo junto con algunas líneas tangentes. Observe cómo la línea tangente de la izquierda es empinada, hacia arriba, correspondiente a un gran valor de$f'$. A la derecha, la línea tangente es empinada, hacia abajo, correspondiente a un pequeño valor de$f'$.

$alt$

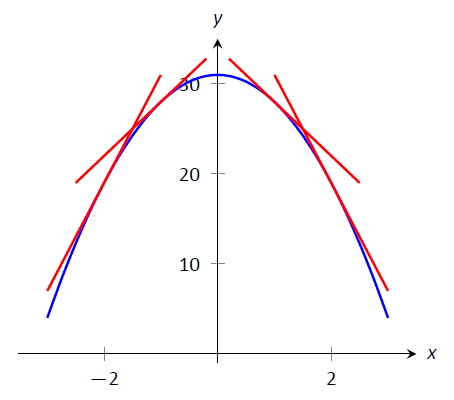
Figura$\PageIndex{2}$: Una función$f$ con una gráfica cóncava hacia abajo. Observe cómo las pendientes de las líneas tangentes, al mirar de izquierda a derecha, están disminuyendo.

Si una función está aumentando y cóncava hacia abajo, entonces su tasa de aumento se está desacelerando; está “nivelando”. Si la función es decreciente y cóncava hacia abajo, entonces la tasa de disminución es decreciente. La función está disminuyendo a un ritmo cada vez más rápido.

Nota: Un mnemotécnico para recordar lo que significa cóncavo arriba/abajo es: “Cóncavo arriba es como una copa; el abajo cóncavo es como un ceño fruncido Es cierto que es terrible, pero funciona.

Nuestra definición de cóncavo hacia arriba y cóncavo hacia abajo se da en términos de cuándo la primera derivada está aumentando o disminuyendo. Podemos aplicar los resultados de la sección anterior y para encontrar intervalos en los que una gráfica sea cóncava hacia arriba o hacia abajo. Es decir, reconocemos que$f'$ va en aumento cuando$f''>0$, etc.

Teorema$\PageIndex{1}$: Test for Concavity

Dejar$f$ ser dos veces diferenciable en un intervalo$I$. La gráfica de$f$ es cóncava hacia arriba si está$f''>0$ encendida$I$ y es cóncava hacia abajo si está$f''<0$ encendida$I$.

$alt$

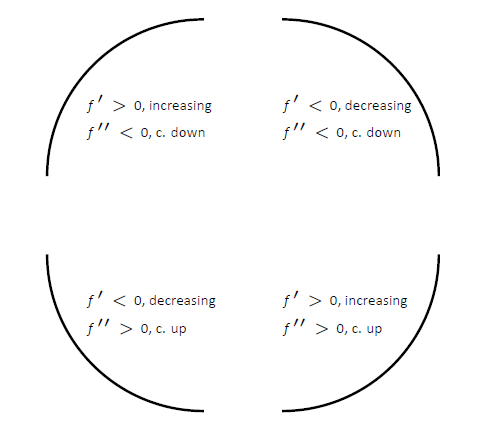
Figura$\PageIndex{3}$: Demostrando las 4 formas en que la concavidad interactúa con el aumento/decreciente, junto con las relaciones con la primera y la segunda derivada.

Nota: Geométricamente hablando, una función es cóncava hacia arriba si su gráfica se encuentra por encima de sus líneas tangentes. Una función es cóncava hacia abajo si su gráfica se encuentra debajo de sus líneas tangentes.

Si es importante saber dónde es cóncava una gráfica arriba/abajo, tiene sentido que también sean importantes los lugares donde la gráfica cambia de una a otra. Esto nos lleva a una definición.

Definición: Punto de inflexión

Un punto de inflexión es un punto en la gráfica$f$ en el que cambia la concavidad de$f$ los cambios.

La figura$\PageIndex{4}$ muestra una gráfica de una función con puntos de inflexión etiquetados.

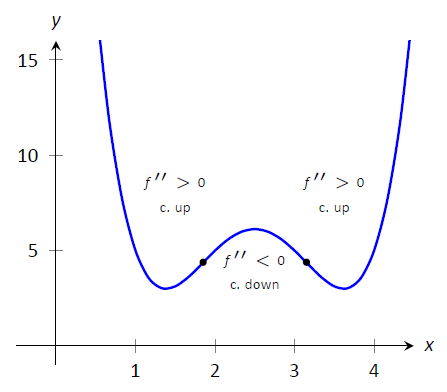
$la función para esta imagen es x^5-3x^3+2x+1$

Figura$\PageIndex{4}$: Gráfica de una función con sus puntos de inflexión marcados. También se indican los intervalos donde cóncavos arriba/abajo.

Si la concavidad de$f$ los cambios en un punto$(c,f(c))$, entonces$f'$ está cambiando de aumentar a disminuir (o, disminuyendo a aumentar) en$x=c$. Eso significa que el signo de$f''$ está cambiando de positivo a negativo (o, negativo a positivo) en$x=c$. Esto lleva al siguiente teorema.

Teorema$\PageIndex{2}$: Points of Inflection

Si$(c,f(c))$ es un punto de inflexión en la gráfica de$f$, entonces cualquiera$f''=0$ o no$f''$ se define en$c$.

Se han identificado los conceptos de concavidad y puntos de inflexión. Ahora es el momento de practicar el uso de estos conceptos; dada una función, deberíamos poder encontrar sus puntos de inflexión e identificar intervalos en los que es cóncava hacia arriba o hacia abajo. Lo hacemos en los siguientes ejemplos.

Ejemplo$\PageIndex{1}$: Finding intervals of concave up/down, inflection points

Vamos$f(x)=x^3-3x+1$. Encuentra los puntos de inflexión de$f$ y los intervalos en los que es cóncavo arriba/abajo.

Solución

Empezamos por encontrar$f'(x)=3x^2-3$ y$f''(x)=6x$. Para encontrar los puntos de inflexión, utilizamos Teorema$\PageIndex{2}$ y encontramos dónde$f''(x)=0$ o dónde$f''$ está indefinido. Nos encontramos siempre$f''$ se define, y es 0 sólo cuando$x=0$. Entonces el punto$(0,1)$ es el único punto posible de inflexión.

Este posible punto de inflexión divide la línea real en dos intervalos,$(-\infty,0)$ y$(0,\infty)$. Utilizamos un proceso similar al utilizado en la sección anterior para determinar el aumento/decreciente. Escoge cualquiera$c<0$;$f''(c)<0$ así$f$ es cóncavo hacia abajo$(-\infty,0)$. Escoge cualquiera$c>0$;$f''(c)>0$ así$f$ es cóncavo hacia arriba$(0,\infty)$. Dado que la concavidad cambia en$x=0$, el punto$(0,1)$ es un punto de inflexión.

$alt$

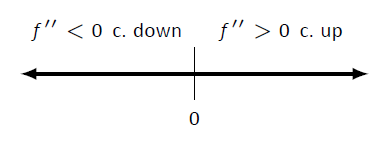
Figura$\PageIndex{5}$: Una línea numérica que determina la concavidad de$f$ en Ejemplo$\PageIndex{1}$.

La línea numérica de la Figura$\PageIndex{5}$ ilustra el proceso de determinación de la concavidad; la Figura$\PageIndex{6}$ muestra una gráfica de$f$ y$f''$, confirmando nuestros resultados. Observe cómo$f$ es cóncavo hacia abajo precisamente cuando$f''(x)<0$ y cóncava hacia arriba cuando$f''(x)>0$.

$alt$

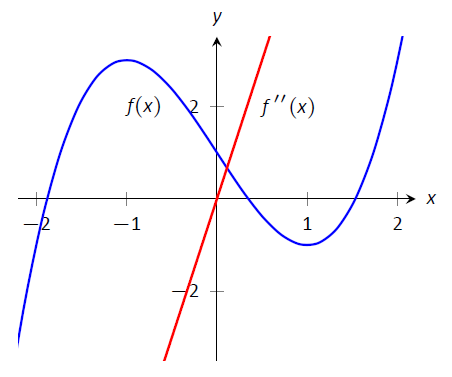
Figura$\PageIndex{6}$: Un gráfico de$f(x)$ utilizado en el Ejemplo$\PageIndex{1}$

Ejemplo$\PageIndex{2}$: Finding intervals of concave up/down, inflection points

Vamos$f(x)=x/(x^2-1)$. Encuentra los puntos de inflexión de$f$ y los intervalos en los que es cóncavo arriba/abajo.

Solución

Tenemos que encontrar$f'$ y$f''$. Usando la regla del cociente y simplificando, encontramos

\[f'(x)=\frac{-(1+x^2)}{(x^2-1)^2} \quad \text{and}\quad f''(x) = \frac{2x(x^2+3)}{(x^2-1)^3}.\]

Para encontrar los posibles puntos de inflexión, buscamos encontrar dónde$f''(x)=0$ y dónde no$f''$ está definido. Resolver$f''x)=0$ reduce a resolver$2x(x^2+3)=0$; encontramos$x=0$. Encontramos que no$f''$ se define cuando$x=\pm 1$, para entonces el denominador de$f''$ es 0. También notamos que$f$ en sí mismo no se define en$x=\pm1$, teniendo un dominio de$(-\infty,-1)\cup(-1,1)\cup(1,\infty)$. Dado que el dominio de$f$ es la unión de tres intervalos, tiene sentido que la concavidad de$f$ pueda cambiar a través de intervalos. Técnicamente no podemos decir que$f$ tenga un punto de inflexión al$x=\pm1$ ya que no forman parte del dominio, pero aún debemos considerar que estos$x$ valores son importantes y los incluiremos en nuestra recta numérica.

$x$Los valores importantes a los que la concavidad podría cambiar son$x=-1$,$x=0$ y$x=1$, que dividen la línea numérica en cuatro intervalos como se muestra en la Figura$\PageIndex{7}$. Determinamos la concavidad en cada uno. Tenga en cuenta que lo único que nos preocupa es el signo de$f''$ en el intervalo.

Intervalo 1,$(-\infty,-1)$: Seleccione un número$c$ en este intervalo con una magnitud grande (por ejemplo,$c=-100$). El denominador de$f''(x)$ será positivo. En el numerador, el$(c^2+3)$ será positivo y el$2c$ término será negativo. Así el numerador es negativo y$f''(c)$ es negativo. Concluimos que$f$ es cóncavo hacia abajo$(-\infty,-1)$.

Intervalo 2,$(-1,0)$: Para cualquier número$c$ en este intervalo, el término$2c$ en el numerador será negativo, el término$(c^2+3)$ en el numerador será positivo, y el término$(c^2-1)^3$ en el denominador será negativo. Así$f''(c)>0$ y$f$ es cóncava hacia arriba en este intervalo.

Intervalo 3,$(0,1)$: Cualquier número$c$ en este intervalo será positivo y “pequeño”. Así el numerador es positivo mientras que el denominador es negativo. Así$f''(c)<0$ y$f$ es cóncava hacia abajo en este intervalo.

Intervalo 4,$(1,\infty)$: Elija un valor grande para$c$. Es evidente que$f''(c)>0$, por lo que concluimos que$f$ es cóncavo hacia arriba$(1,\infty)$.

$alt$

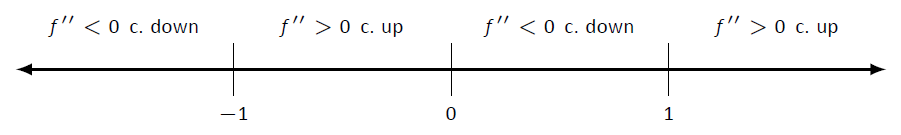
Figura$\PageIndex{7}$: Línea numérica para$f$ en Ejemplo$\PageIndex{2}$

Concluimos que$f$ es cóncavo hacia arriba$(-1,0)\cup(1,\infty)$ y cóncavo hacia abajo$(-\infty,-1)\cup(0,1)$. Sólo hay un punto de inflexión,$(0,0)$, como no$f$ se define en$x=\pm 1$. Nuestro trabajo está confirmado por la gráfica de$f$ en Figura$\PageIndex{8}$. Observe cómo$f$ es cóncavo hacia arriba cuando$f''$ es positivo, y cóncavo hacia abajo cuando$f''$ es negativo.

$alt$

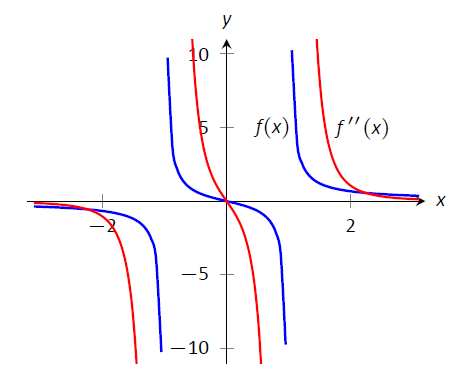
Figura$\PageIndex{8}$: Una gráfica de$f(x)$ y$f''(x)$ en el Ejemplo$\PageIndex{2}$

Recordemos que los máximos y mínimos relativos de$f$ se encuentran en puntos críticos de$f$; es decir, se encuentran cuando$f'(x)=0$ o cuando$f'$ está indefinido. De igual manera, los máximos y mínimos relativos de$f'$ se encuentran cuando$f''(x)=0$ o cuando$f''$ está indefinido; tenga en cuenta que estos son los puntos de inflexión de$f$.

¿Qué significa un “máximo relativo de$f'$"? La derivada mide la tasa de cambio de$f$; maximizando$f'$ significa encontrar el dónde$f$ está aumentando más — donde$f$ tiene la línea tangente más pronunciada. Se puede hacer una declaración similar para minimizar$f'$; corresponde a donde$f$ tiene la línea tangente inclinada negativa más pronunciada.

Utilizamos este concepto en el siguiente ejemplo.

Ejemplo$\PageIndex{3}$: Understanding inflection points

Las ventas de un determinado producto a lo largo de un lapso de tres años se modelan por$S(t)= t^4-8t^2+20$, donde$t$ está el tiempo en años, que se muestra en la Figura$\PageIndex{9}$. A lo largo de los dos primeros años, las ventas están disminuyendo. Encuentra el punto en el que las ventas están disminuyendo a su mayor ritmo.

$alt$

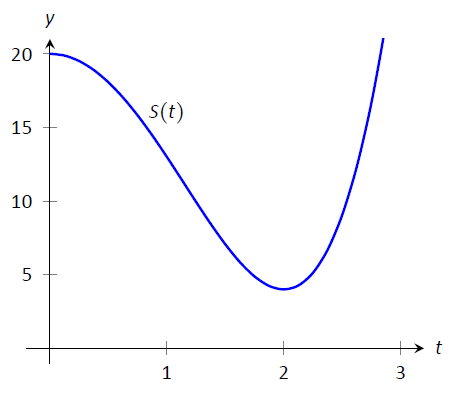
Figura$\PageIndex{9}$: Una gráfica de$S(t)$ en Ejemplo$\PageIndex{3}$, modelando la venta de un producto a lo largo del tiempo.

Queremos maximizar la tasa de disminución, es decir, queremos encontrar dónde$S'$ tiene un mínimo. Para ello, encontramos dónde$S''$ está 0. Nos encontramos$S'(t)=4t^3-16t$ y$S''(t)=12t^2-16$. Estableciendo$S''(t)=0$ y resolviendo, obtenemos$t=\sqrt{4/3}\approx 1.16$ (ignoramos el valor negativo de$t$ ya que no se encuentra en el dominio de nuestra función$S$).

Este es tanto el punto de inflexión como el punto de máxima disminución. Este es el punto en el que las cosas primero empiezan a buscar a la empresa. Después del punto de inflexión, aún tardará algún tiempo antes de que las ventas comiencen a aumentar, pero al menos las ventas no están disminuyendo tan rápido como lo habían sido.

Una gráfica de$S(t)$ y$S'(t)$ se da en la Figura$\PageIndex{10}$. Cuando$S'(t)<0$, las ventas están disminuyendo; tenga en cuenta cómo en$t\approx 1.16$,$S'(t)$ se minimiza. Es decir, las ventas están disminuyendo al ritmo más rápido en$t\approx 1.16$. En el intervalo de$(1.16,2)$,$S$ está disminuyendo pero cóncavo hacia arriba, por lo que la disminución en las ventas está “nivelando”.

$alt$

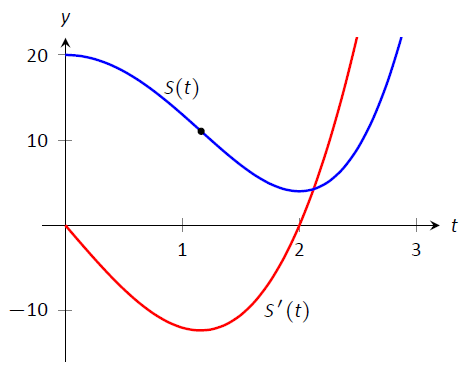
Figura$\PageIndex{10}$: Una gráfica de$S(t)$ en Ejemplo$\PageIndex{3}$ junto con$S'(t)$.

No todos los puntos críticos corresponden a un extremo relativo;$f(x)=x^3$ tiene un punto crítico en$(0,0)$ pero ningún máximo o mínimo relativo. De igual manera, solo porque no$f''(x)=0$ podemos concluir cambios de concavidad en ese momento. Antes tuvimos cuidado de usar la terminología "posible punto de inflexión” ya que necesitábamos verificar si la concavidad cambiaba. El ejemplo canónico de$f''(x)=0$ sin cambio de concavidad es$f(x)=x^4$. En$x=0$,$f''(x)=0$ pero siempre$f$ es cóncavo hacia arriba, como se muestra en la Figura$\PageIndex{11}$.

$alt$

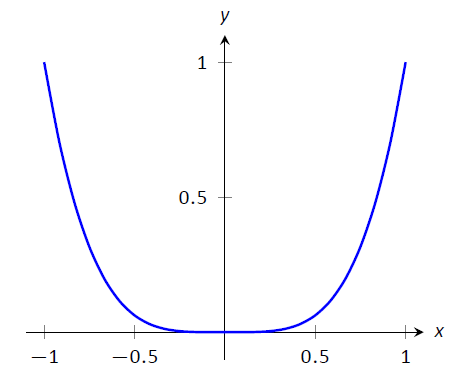
Figura$\PageIndex{11}$: Una gráfica de$f(x) = x^4$. Claramente siempre$f$ es cóncava hacia arriba, a pesar de que$f''(x) = 0$ cuando$x=0$. Si este ejemplo, el posible punto de inflexión no$(0,0)$ es un punto de inflexión.

Nota: Una nota sobre la concavidad:

En general, la concavidad sólo puede cambiar donde o bien la segunda derivada es 0, donde hay una asíntota vertical, o (rara en la práctica) donde la segunda derivada es indefinida. Pero la concavidad no\ emph {tiene} que cambiar en estos lugares. Por ejemplo, si$f(x)=x^4$, entonces$f''(0)=0$, pero no hay cambio de concavidad a 0 y tampoco hay punto de inflexión ahí. Además, si$f(x)=1/x^2$, entonces$f$ tiene una asíntota vertical a 0, pero no hay cambio en la concavidad a 0.

La Segunda Prueba Derivada

La primera derivada de una función nos dio una prueba para encontrar si un valor crítico correspondía a un máximo relativo, mínimo, o ninguno de los dos. La segunda derivada nos da otra forma de probar si un punto crítico es un máximo o mínimo local. El siguiente teorema afirma oficialmente algo que es intuitivo: si se produce un valor crítico en una región donde una función$f$ es cóncava hacia arriba, entonces ese valor crítico debe corresponder a un mínimo relativo de$f$, etc. Ver Figura$\PageIndex{12}$ para una visualización de esto.

$alt$

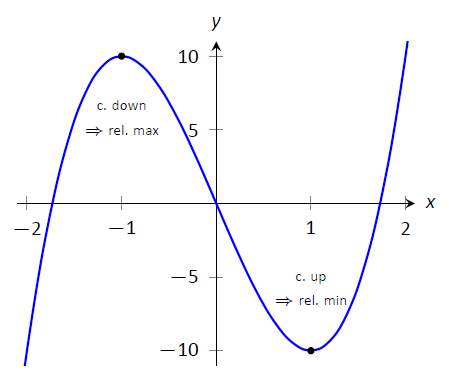
Figura$\PageIndex{12}$: Demostrando el hecho de que los máximos relativos ocurren cuando la gráfica es cóncava hacia abajo y los mínimos relacionados ocurren cuando la gráfica es cóncava hacia arriba.

Teorema$\PageIndex{3}$: The Second Derivative Test

Dejar$c$ ser un valor crítico de$f$ donde$f''(c)$ se define.

Si$f''(c)>0$, entonces$f$ tiene un mínimo local en$(c,f(c))$.
Si$f''(c)<0$, entonces$f$ tiene un máximo local en$(c,f(c))$.

La Prueba de Segunda Derivada se relaciona con la Prueba de Primera Derivada de la siguiente manera. Si$f''(c)>0$, entonces la gráfica es cóncava hacia arriba en un punto crítico$c$ y en$f'$ sí misma va creciendo. Desde$f'(c)=0$ y$f'$ está creciendo en$c$, entonces debe pasar de negativo a positivo en$c$. Esto significa que la función va de disminuir a aumentar, indicando un mínimo local en$c$.

Ejemplo$\PageIndex{4}$: Using the Second Derivative Test

Vamos$f(x)=100/x + x$. Encuentre los puntos críticos$f$ y use la Prueba de Segunda Derivada para etiquetarlos como máximos o mínimos relativos.

Solución

Encontramos$f'(x)=-100/x^2+1$ y$f''(x) = 200/x^3.$ nos fijamos$f'(x)=0$ y resolvemos$x$ para encontrar los valores críticos (tenga en cuenta que f'\ no se define en$x=0$, pero tampoco$f$ lo es así que este no es un valor crítico.) Encontramos que los valores críticos son$x=\pm 10$. Evaluando$f''$ en$x=10$ da$0.1>0$, por lo que hay un mínimo local en$x=10$. Evaluando$f''(-10)=-0.1<0$, determinando un máximo relativo a$x=-10$. Estos resultados se confirman en la Figura$\PageIndex{13}$.

$alt$

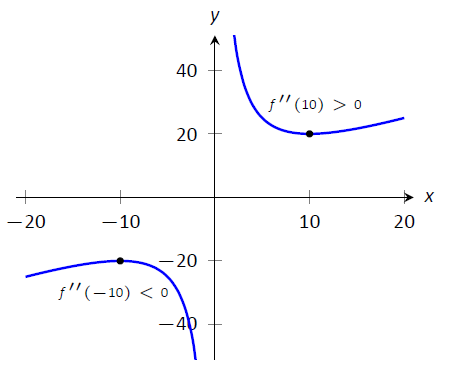
Figura$\PageIndex{13}$: Una gráfica de$f(x)$ en Ejemplo$\PageIndex{4}$. La segunda derivada se evalúa en cada punto crítico. Cuando la gráfica es cóncava hacia arriba, el punto crítico representa un mínimo local; cuando la gráfica es cóncava hacia abajo, el punto crítico representa un máximo local.

Hemos estado aprendiendo cómo la primera y la segunda derivada de una función relacionan la información sobre la gráfica de esa función. Se han encontrado intervalos de incremento y decreciente, intervalos donde la gráfica es cóncava hacia arriba y hacia abajo, junto con las ubicaciones de extremos relativos y puntos de inflexión. En el Capítulo 1 vimos cómo los límites explicaban el comportamiento asintótico. En la siguiente sección combinamos toda esta información para producir bocetos precisos de funciones.