3.5: Croquizado de Curva

Hemos estado aprendiendo cómo podemos entender el comportamiento de una función a partir de su primera y segunda derivada. Si bien hemos estado tratando las propiedades de una función por separado (creciente y decreciente, cóncava hacia arriba y cóncava hacia abajo, etc.), las combinamos aquí para producir una gráfica precisa de la función sin trazar muchos puntos extraños.

¿Por qué molestarse? Las utilidades gráficas son muy accesibles, ya sea en una computadora, una calculadora de mano o un teléfono inteligente. Estos recursos suelen ser muy rápidos y precisos. Veremos que nuestro método no es particularmente rápido —requerirá tiempo (pero no es difícil). Entonces otra vez: ¿por qué molestarse?

Estamos tratando de entender el comportamiento de una\(f\) función a partir de la información dada por sus derivadas. Si bien todas las derivadas de una función transmiten información al respecto, resulta que “la mayor parte” del comportamiento que nos importa se explica por\(f'\) y\(f''\). Comprender las interacciones entre la gráfica de\(f\) y\(f'\) y\(f'\) es importante. Para obtener esta comprensión, se podría argumentar que todo lo que se necesita es mirar muchas gráficas. Esto es cierto hasta cierto punto, pero es algo similar a afirmar que uno entiende cómo funciona un motor después de mirar solo imágenes. Es cierto que se transmitirán las ideas básicas, pero el acceso “práctico” aumenta la comprensión.

La siguiente Idea Clave resume lo que hemos aprendido hasta ahora que es aplicable al bosquejar gráficas de funciones y da un marco para armar esa información. Le siguen varios ejemplos.

Idea Clave 4: Croquizado de Curvas

Para producir un boceto preciso de una función dada\(f\), considere los siguientes pasos.

1. Encuentra el dominio de\(f\). Generalmente, asumimos que el dominio es toda la línea real luego encontramos restricciones, como donde un denominador es 0 o donde aparecen negativos bajo el radical.
2. Encuentra los valores críticos de\(f\).
3. Encuentra los posibles puntos de inflexión de\(f\).
4. Encuentre la ubicación de cualquier asíntota vertical de\(f\) (generalmente realizada en conjunto con el ítem 1 anterior).
5. Considerar los límites\(\displaystyle \lim_{x\to-\infty}f(x)\) y\(\displaystyle \lim_{x\to\infty}f(x)\) determinar el comportamiento final de la función.
6. Cree una línea numérica que incluya todos los puntos críticos, posibles puntos de inflexión y ubicaciones de asíntotas verticales. Para cada intervalo creado, determine si\(f\) es creciente o decreciente, cóncavo hacia arriba o hacia abajo.
7. Evaluar\(f\) en cada punto crítico y posible punto de inflexión. Trazar estos puntos en un conjunto de ejes. Conectar estos puntos con curvas que exhiban la concavidad adecuada. Esbozar asíntotas\(x\) e\(y\) interceptaciones en su caso.

Ejemplo\(\PageIndex{1}\): curve sketching

Usa Key Idea 4 para bosquejar\(f(x) = 3x^3-10x^2+7x+5\).

Solución

1. El dominio de\(f\) es toda la línea real; no hay valores\(x\) para los cuales no\(f(x)\) está definido.
2. Encuentra los valores críticos de\(f\). Nosotros computamos\(f'(x) = 9x^2-20x+7\). Usa la Fórmula Cuadrática para encontrar las raíces de\(f'\):
   $$x =\ frac {20\ pm\ sqrt {(-20) ^2-4 (9) (7)}} {2 (9)} =\ frac19\ left (10\ pm\ sqrt {37}\ right)\ Rightarrow x\ approx 0.435, 1.787. $$
3. Encuentra los posibles puntos de inflexión de\(f\). Cómputos\(f''(x) = 18x-20\). Tenemos
   $$f'p (x) = 0\ Rightarrow x= 10/9\ approx 1.111. $$
4. No hay asíntotas verticales.
5. Determinamos el comportamiento final usando límites a medida que se\(x\) aproxima al\(\pm\) infinito. $$\ lim_ {x\ a -\ infty} f (x) = -\ infty\ qquad\ lim_ {x\ a\ infty} f (x) =\ infty. $$No tenemos asíntotas horizontales.
6. Colocamos los valores\(x=(10\pm\sqrt{37})/9\) y\(x=10/9\) en una recta numérica, como se muestra en la Figura\(\PageIndex{1}\). Marcamos cada subintervalo como creciente o decreciente, cóncavo hacia arriba o hacia abajo, utilizando las técnicas utilizadas en las Secciones 3.3 y 3.4.

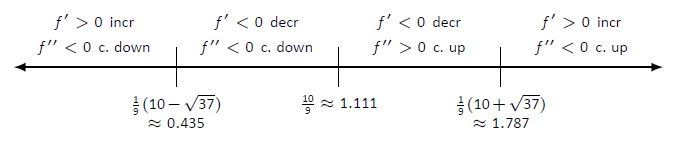
Figura\(\PageIndex{1}\): Línea numérica para\(f\) en Ejemplo\(\PageIndex{1}\).

7. Trazamos los puntos apropiados en ejes como se muestra en la Figura\(\PageIndex{2a}\) y conectamos los puntos con líneas rectas. En la Figura\(\PageIndex{2b}\) ajustamos estas líneas para demostrar la concavidad adecuada. Nuestra curva cruza el\(y\) eje en\(y=5\) y cruza el\(x\) eje cercano\(x=-0.424\). En la Figura\(\PageIndex{2c}\) mostramos una gráfica de\(f\) dibujado con un programa de computadora, verificando la exactitud de nuestro boceto.

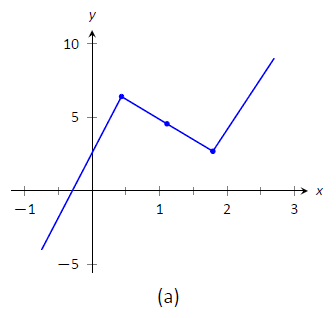
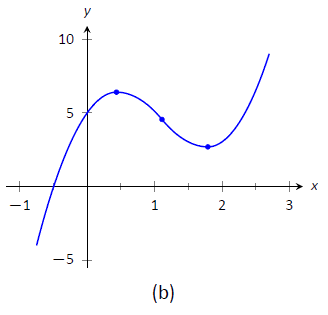
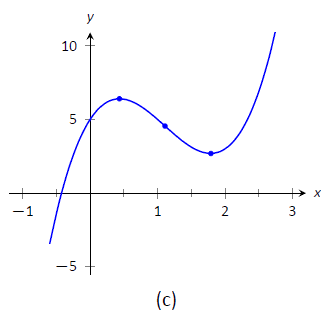
Figura\(\PageIndex{2}\): Croquizar\(f\) en Ejemplo\(\PageIndex{1}\).

Ejemplo\(\PageIndex{2}\): Curve sketching

Croquis\(f(x) = \dfrac{x^2-x-2}{x^2-x-6}\).

Solución

Nuevamente seguimos los pasos descritos en la Idea Clave 4.

1. Al determinar el dominio, asumimos que es todo números reales y busca restricciones. Nos encontramos con que en\(x=-2\) y\(x=3\), no\(f(x)\) está definido. Entonces el dominio de\(f\) es\(D = \{\text{real numbers } x\ | \ x\neq -2,3\}\).
2. Para encontrar los valores críticos de\(f\), primero encontramos\(f'(x)\). Usando la regla de cociente, encontramos$$f' (x) =\ frac {-8x+4} {(x^2+x-6) ^2} =\ frac {-8x+4} {(x-3) ^2 (x+2) ^2}. $$\(f'(x) = 0\) cuando\(x = 1/2\), y no\(f'\) está definido cuando\(x=-2,3\). Ya que\(f'\) es indefinido sólo cuando\(f\) es, estos no son valores críticos. El único valor crítico es\(x=1/2\).
3. Para encontrar los posibles puntos de inflexión, encontramos\(f''(x)\), nuevamente empleando la Regla del Cociente: $$f "(x) =\ frac {24x^2-24x+56} {(x-3) ^3 (x+2) ^3}. $$Encontramos que nunca\(f''(x)\) es 0 (estableciendo el numerador igual a 0 y resolviendo para\(x\), encontramos que las únicas raíces a esta cuadrática son imaginarias) y\(f'\) es indefinido cuando\(x=-2,3\). Por lo tanto, la concavidad posiblemente solo cambiará en\(x=-2\) y\(x=3\).
4. Las asíntotas verticales de\(f\) están en\(x=-2\) y\(x=3\), los lugares donde\(f\) está indefinido.
5. Hay una asíntota horizontal de\(y=1\), as\(\lim_{x\to -\infty}f(x) = 1\) y\(\lim_{x\to\infty}f(x) =1\).
6. Colocamos los valores\(x=1/2\),\(x=-2\) y\(x=3\) en una recta numérica como se muestra en la Figura\(\PageIndex{3}\). Marcamos en cada intervalo si\(f\) es creciente o decreciente, cóncavo hacia arriba o hacia abajo. Vemos que\(f\) tiene un máximo relativo a\(x=1/2\); la concavidad cambia solo en las asíntotas verticales.

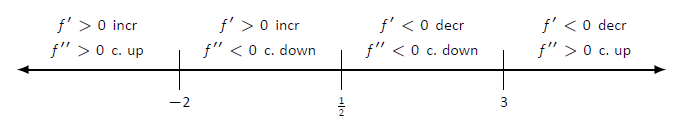
Figura\(\PageIndex{3}\): Línea numérica para\(f\) en Ejemplo\(\PageIndex{2}\)

7. En Figura\(\PageIndex{4a}\), trazamos los puntos de la recta numérica en un conjunto de ejes y conectamos los puntos con líneas rectas para tener una idea general de cómo es la función (estas líneas efectivamente solo transmiten información de aumento/disminución). En la Figura\(\PageIndex{4b}\), ajustamos la gráfica con la concavidad apropiada. También mostramos\(f\) cruzando el\(x\) eje en\(x=-1\) y\(x=2\).

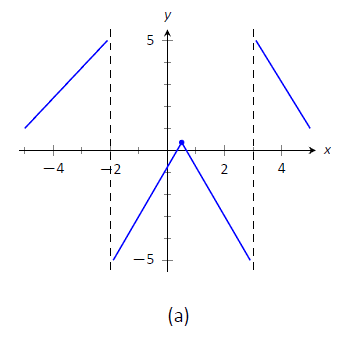
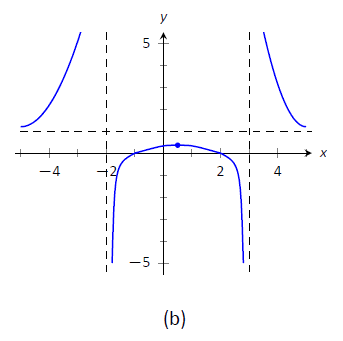
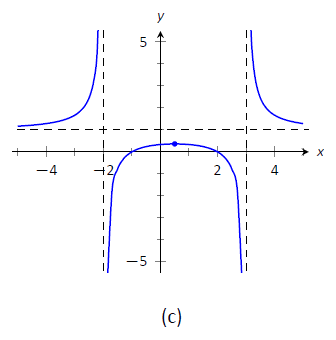
Figura\(\PageIndex{4}\): Croquizar\(f\) en Ejemplo\(\PageIndex{2}\).

La figura\(\PageIndex{4c}\) muestra una gráfica generada por computadora de\(f\), que verifica la precisión de nuestro boceto.

Ejemplo\(\PageIndex{3}\): Curve sketching

Sketch\(f(x) = \frac{5(x-2)(x+1)}{x^2+2x+4}.\)

Solución

Nuevamente seguimos Key Idea 4

1. Suponemos que el dominio de\(f\) es todo números reales y consideramos restricciones. Las únicas restricciones vienen cuando el denominador es 0, pero esto nunca ocurre. Por lo tanto el dominio de\(f\) es todo números reales,\(\mathbb{R}\).
2. Encontramos los valores críticos de\(f\) estableciendo\(f'(x)=0\) y resolviendo para\(x\). Encontramos
   $$f' (x) =\ frac {15x (x+4)} {(x^2+2x+4) ^2}\ quad\ Rightarrow\ quad f' (x) = 0\ text {when}\ x=-4,0. $$
3. Encontramos los posibles puntos de inflexión resolviendo\(f''(x) = 0\) para\(x\). Encontramos
   $$f'p (x) = -\ frac {30x^3+180x^2-240} {(x^2+2x+4) ^3} .$$ El cúbico en el numerador no factorial muy “muy bien”. En cambio, aproximamos las raíces en\(x= -5.759\),\(x=-1.305\) y\(x=1.064\).
4. No hay asíntotas verticales.
5. Tenemos una asíntota horizontal de\(y=5\), as\(\lim_{x\to-\infty}f(x) = \lim_{x\to\infty}f(x) = 5\).
6. Colocamos los puntos críticos y posibles puntos en una recta numérica como se muestra en la Figura\(\PageIndex{5}\) y marcamos cada intervalo como aumento/decreciente, cóncavo arriba/abajo apropiadamente.

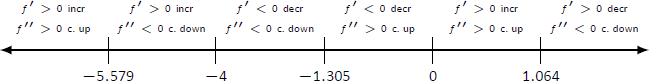
Figura\(\PageIndex{5}\): Línea numérica para\(f\) en Ejemplo\(\PageIndex{3}\).

7. En Figura\(\PageIndex{6a}\) trazamos los puntos significativos de la recta numérica así como las dos raíces de\(f\),\(x=-1\) y\(x=2\), y conectamos los puntos con líneas rectas para obtener una impresión general sobre la gráfica. En Figura\(\PageIndex{6b}\), agregamos concavidad. La figura\(\PageIndex{6c}\) muestra una gráfica generada por computadora de\(f\), afirmando nuestros resultados.

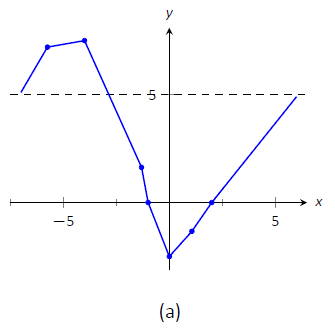
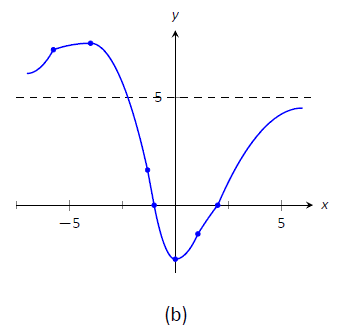
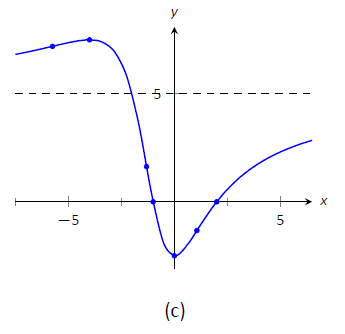
Figura\(\PageIndex{6}\): Croquizar\(f\) en Ejemplo\(\PageIndex{3}\).

En cada uno de nuestros ejemplos, encontramos algunos puntos significativos en la gráfica\(f\) que correspondían a cambios en aumento/decreciente o concavidad. Conectamos estos puntos con líneas rectas, luego ajustamos por concavidad, y terminamos mostrando una gráfica muy precisa, generada por computadora.

¿Por qué son tan buenos los gráficos por computadora? No es porque las computadoras sean “más inteligentes” que nosotros. Más bien, es en gran parte porque las computadoras son mucho más rápidas en la computación que nosotros. En general, las computadoras grafican funciones de manera muy similar a la mayoría de los estudiantes cuando aprenden por primera vez a dibujar gráficas: trazan puntos igualmente espaciados, luego conectan los puntos usando líneas. Al usar muchos puntos, las líneas de conexión son cortas y la gráfica se ve suave.

Esto hace un buen trabajo de graficar en la mayoría de los casos (de hecho, este es el método utilizado para muchas gráficas en este texto). Sin embargo, en regiones donde la gráfica es muy “curvilínea”, esto puede generar bordes afilados notables en la gráfica a menos que se use una gran cantidad de puntos. Los sistemas de álgebra computacional de alta calidad, como Mathematica, utilizan algoritmos especiales para trazar muchos puntos solo donde el gráfico es “curvilíneo”.

En la Figura\(\PageIndex{7}\),\(y=\sin x\) se da una gráfica de, generada por Mathematica. Los puntos pequeños representan cada uno de los lugares que Mathematica muestreó la función. Observe cómo en las “curvas” de\(\sin x\), se utilizan muchos puntos; donde\(\sin x\) es relativamente recto, se utilizan menos puntos. (También se utilizan muchos puntos en los puntos finales para garantizar que el “comportamiento final” sea preciso).

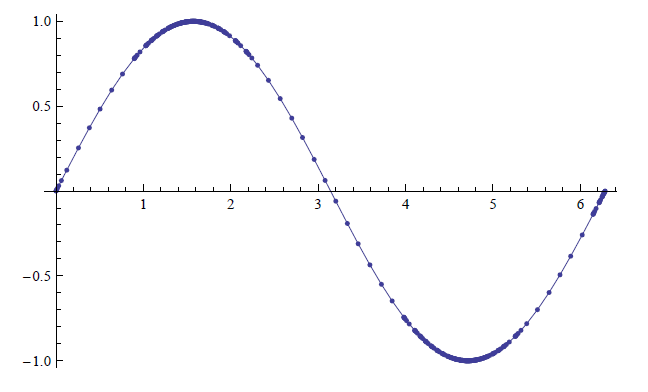
Figura\(\PageIndex{7}\): Un gráfico de\(y=\sin x\) generado por Mathematica.

¿Cómo sabe Mathematica dónde está el gráfico “curvilíneo”? Cálculo. Cuando estudiamos la curvatura en un capítulo posterior, veremos cómo la primera y la segunda derivada de una función trabajan juntas para proporcionar una medición de la “curva”. Mathematica emplea algoritmos para determinar regiones de “alta curvatura"' y grafica puntos extra allí.

Nuevamente, el objetivo de esta sección no es “Cómo graficar una función cuando no hay computadora para ayudar”. Más bien, el objetivo es “Entender que la forma de la gráfica de una función se determina en gran medida al comprender el comportamiento de la función en algunos lugares clave”. En Ejemplo\(\PageIndex{3}\), pudimos esbozar con precisión una gráfica complicada usando solo 5 puntos y conocimiento de asíntotas!

Hay muchas aplicaciones de nuestra comprensión de derivados más allá del boceto de curvas. El siguiente capítulo explora algunas de estas aplicaciones, demostrando solo algunos tipos de problemas que pueden resolverse con un conocimiento básico de diferenciación.

Colaboradores y Atribuciones

• Template:ContribApexCalc
• Template:ContribMarshall