Inicio
Matemáticas
Libro: Cálculo (Apex)
7: Aplicaciones de Integración
7.2: Volumen por Área Transversal- Métodos de Disco y Arandela

7.2: Volumen por Área Transversal- Métodos de Disco y Arandela

Última actualización
Guardar como PDF

Page ID: 111788

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

El volumen de un cilindro derecho general, como se muestra en la Figura$\PageIndex{1}$, es

\[\text{Area of the base $\times$ height.}\]

Podemos usar este hecho como el bloque de construcción para encontrar volúmenes de una variedad de formas.

Dado un sólido arbitrario, podemos aproximar su volumen cortándolo en rodajas$n$ finas. Cuando las rebanadas son delgadas, cada rebanada se puede aproximar bien mediante un cilindro general derecho. Así, el volumen de cada rebanada es aproximadamente su$\times$ grosor de área de sección transversal. (Estas rebanadas son los elementos diferenciales).

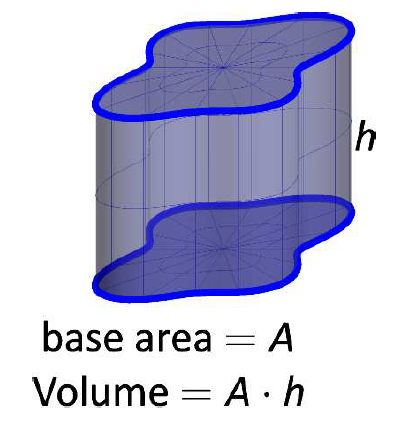
$7.2.1.png$

Figura$\PageIndex{1}$: El volumen de un cilindro general derecho.

Al orientar un sólido a lo largo del$x$ eje, podemos dejar$A(x_i)$ representar el área
de la sección transversal de la$i\,^\text{th}$ rebanada, y dejar$dx_i$ representar el grosor de esta rebanada (el grosor es un pequeño cambio en$x$). El volumen total del sólido es aproximadamente:

\[ \begin{align} \text{Volume} &\approx \sum_{i=1}^n \Big[\text{Area}\ \times\ \text{thickness}\Big] \\ &= \sum_{i=1}^n A(x_i)\ dx_i. \end{align}\]

Reconocer que se trata de una suma de Riemann. Al tomar un límite (ya que el grosor de las rebanadas va a 0) podemos encontrar exactamente el volumen.

Teorema$\PageIndex{1}$: Volume By Cross-Sectional Area

El volumen$V$ de un sólido, orientado a lo largo del$x$ eje con área$A(x)$ de sección transversal de$x=a$ a$x=b$, es

$$V =\ int_a^b A (x)\ dx.\]

Ejemplo$\PageIndex{1}$: Finding the volume of a solid

Encuentra el volumen de una pirámide con una base cuadrada de longitud lateral de 10 pulgadas y una altura de 5 pulgadas.

Solución

Hay muchas maneras de “orientar” la pirámide a lo largo del$x$ eje -eje; la Figura$\PageIndex{2}$ da una de esas vías, con la parte superior puntiaguda de la pirámide en el origen y el$x$ eje pasando por el centro de la base.

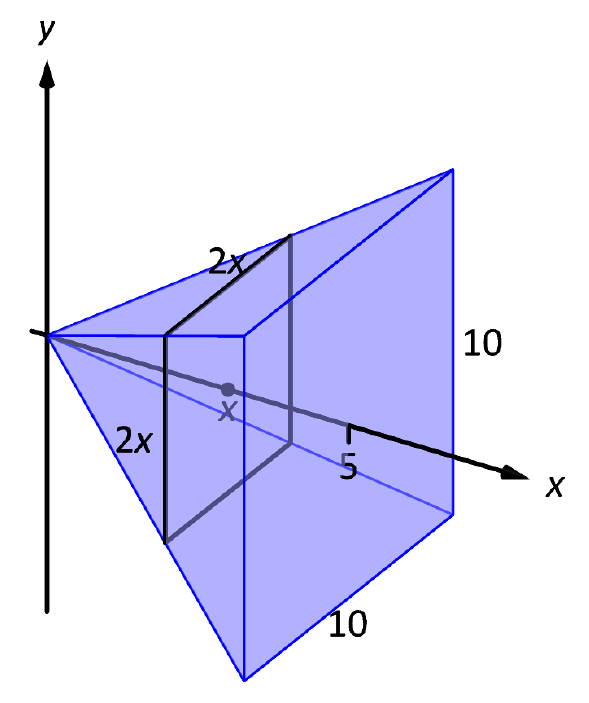
$7.2.2.png$

Figura$\PageIndex{2}$: Orientar una pirámide a lo largo del$x$ eje -eje en Ejemplo$\PageIndex{1}$.

Cada sección transversal de la pirámide es un cuadrado; este es un elemento diferencial de muestra. Para determinar su área$A(x)$, necesitamos determinar las longitudes laterales del cuadrado.

Cuando$x=5$, el cuadrado tiene longitud lateral 10; cuando$x=0$, el cuadrado tiene longitud lateral 0. Dado que los bordes de la pirámide son líneas, es fácil imaginar que cada cuadrado de sección transversal tiene longitud lateral$2x$, dando$A(x) = (2x)^2=4x^2$.

Si uno fuera a cortar una rebanada de la pirámide en$x=3$, como se muestra en la Figura$\PageIndex{3}$, uno tendría una forma con fondo cuadrado y parte superior con lados inclinados. Si la rebanada fuera delgada, tanto los cuadrados inferior como los cuadrados superiores tendrían longitudes de lados de aproximadamente 6, y así el área transversal de la parte inferior y superior sería de aproximadamente 36 pulgadas$^2$. Dejando$\Delta x_i$ representar el grosor de la rebanada, el volumen de esta rebanada sería entonces de aproximadamente$36\Delta x_i\(in$ ^3\).

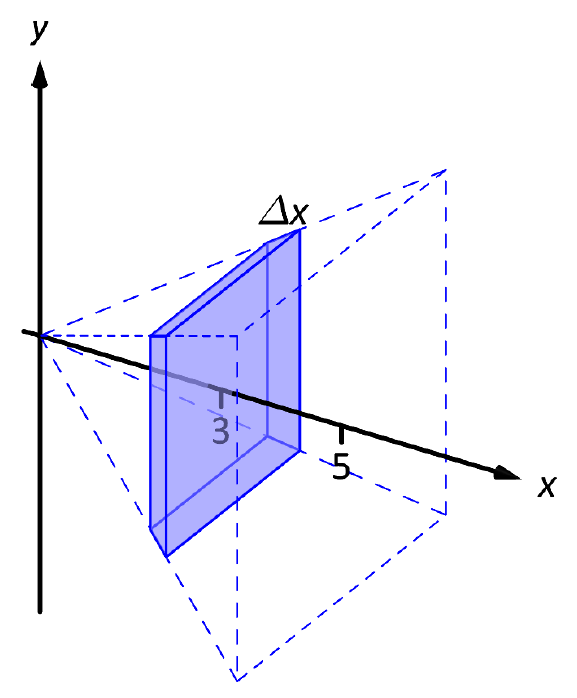
$7.2.3.png$

Figura$\PageIndex{3}$: Cortar una rebanada en la pirámide en Ejemplo$\PageIndex{1}$ en$x=3$.

Cortar la pirámide en$n$ rebanadas divide el volumen total en piezas más$n$ pequeñas igualmente espaciadas, cada una con volumen$(2x_i)^2\Delta x$, donde$x_i$ es la ubicación aproximada de la rebanada a lo largo del$x$ eje y$\Delta x$ representa el grosor de cada rebanada. Se puede aproximar el volumen total de la pirámide resumiendo los volúmenes de estas rebanadas:

$$\ text {Volumen aproximado} =\ suma_ {i=1} ^n (2x_i) ^2\ Delta x.\]

Tomando el límite como$n\to\infty$ da el volumen real de la pirámide; recoginizar esta suma como una suma de Riemann nos permite encontrar la respuesta exacta usando una integral definida, coincidiendo con la integral definida dada por el Teorema$\PageIndex{1}$.

Tenemos

\[\begin{align} V &= \lim_{n\to\infty} \sum_{i=1}^n (2x_i)^2\Delta x\\ &= \int_0^5 4x^2\ dx\\ &= \frac43x^3\Big|_0^5 \\ &=\frac{500}{3}\ \text{in}^3 \approx 166.67\ \text{in}^3.\end{align}\]

Podemos verificar nuestro trabajo consultando la ecuación general para el volumen de una pirámide (ver la contraportada bajo “Volumen de Un Cono General”):

\[\frac13\times \text{area of base}\times \text{height}.\]

Ciertamente, usar esta fórmula de geometría es más rápido que nuestro nuevo método, pero el método basado en cálculo se puede aplicar a mucho más que solo conos.

Un caso especial importante del Teorema$\PageIndex{1}$ es cuando el sólido es un sólido de revolución, es decir, cuando el sólido se forma girando una forma alrededor de un eje.

Comience con una función$y=f(x)$ de$x=a$ a$x=b$. Girar esta curva alrededor de un eje horizontal crea un sólido tridimensional cuyas secciones transversales son discos (círculos delgados). Dejar$R(x)$ representar el radio del disco de sección transversal en$x$; el área de este disco es$\pi R(x)^2$. Aplicando Teorema$\PageIndex{1}$ da el Método del Disco.

Idea Clave 23: El Método del Disco

Deje que se forme un sólido girando la curva$y=f(x)$ de$x=a$ a$x=b$ alrededor de un eje horizontal, y deje$R(x)$ ser el radio del disco de sección transversal en$x$. El volumen del sólido es

$$V =\ pi\ int_a^b R (x) ^2\ dx.\]

Ejemplo$\PageIndex{2}$: Finding volume using the Disk Method

Encuentra el volumen del sólido formado al girar la curva$y=1/x$, de$x=1$ a$x=2$, alrededor del$x$ eje.

Solución

Un boceto puede ayudarnos a entender este problema. En$\PageIndex{4a}$ la Figura$y=1/x$ se esboza la curva junto con el elemento diferencial —un disco—$x$ con radio$R(x)=1/x$. En$\PageIndex{4b}$ la Figura se representa todo el sólido, junto con el elemento diferencial.

El volumen del elemento diferencial mostrado en la parte (a) de la figura es aproximadamente$\pi R(x_i)^2\Delta x$, donde$R(x_i)$ se muestra el radio del disco y$\Delta x$ es el grosor de esa rebanada. El radio$R(x_i)$ es la distancia desde el$x$ eje -hasta la curva, de ahí$R(x_i) = 1/x_i$.

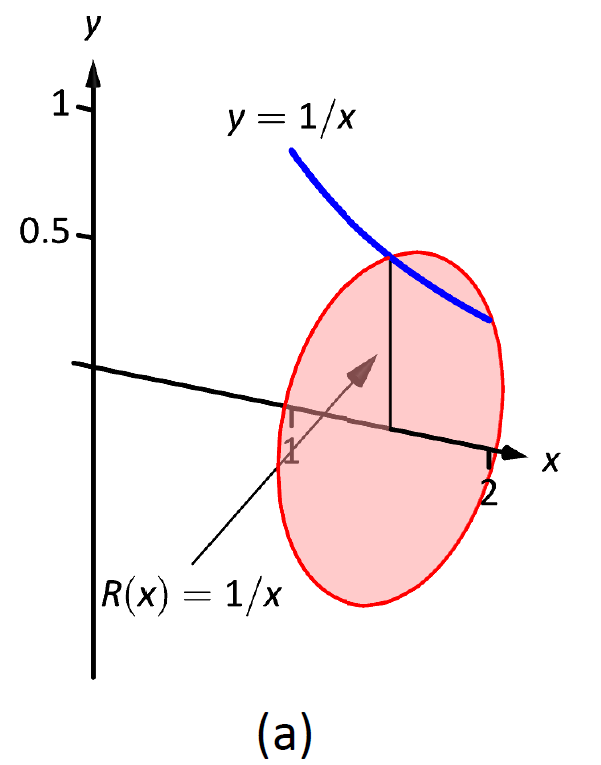
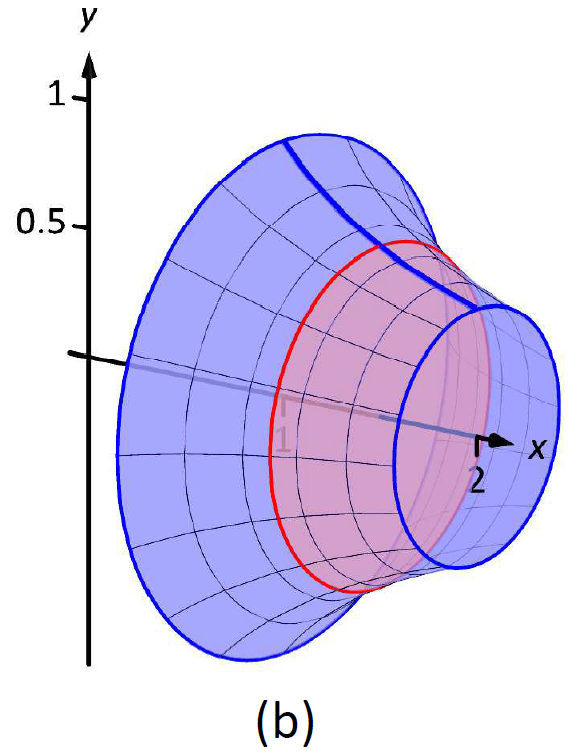
$7.2.4a.png$ $7.2.4b.png$

Figura$\PageIndex{4}$: Esbozo de un sólido en Ejemplo$\PageIndex{2}$.

Rebanando el sólido en$n$ rebanadas igualmente espaciadas, podemos aproximar el volumen total sumando el volumen aproximado de cada rebanada:

$$\ text {Volumen aproximado} =\ suma_ {i=1} ^n\ pi\ izquierda (\ frac1 {x_i}\ derecha) ^2\ Delta x.\]

Tomando el límite de la suma anterior como$n\to\infty$ da el volumen real; reconocer esta suma como una suma de Riemann nos permite evaluar el límite con una integral definida, que coincide con la fórmula dada en la Idea Clave 23:

\[\begin{align} V &= \lim_{n\to\infty}\sum_{i=1}^n \pi \left(\frac1{x_i}\right)^2\Delta x\\ &= \pi\int_1^2 \left(\frac1x\right)^2\ dx \\ &= \pi\int_1^2 \frac1{x^2}\ dx \\ &= \pi\left[-\frac1x\right]\Big|_1^2 \\ &= \pi \left[-\frac12 - \left(-1\right)\right] \\ &= \frac{\pi}{2}\ \text{units}^3.\end{align}\]

Si bien Key Idea 23 se da en términos de funciones de$x$, el principio involucrado puede aplicarse a funciones de$y$ cuando el eje de rotación es vertical, no horizontal. Esto lo demostramos en el siguiente ejemplo.

Ejemplo$\PageIndex{3}$: Finding volume using the Disk Method

Encuentra el volumen del sólido formado girando la curva$y=1/x$, desde$x=1$ hasta$x=2$, alrededor del$y$ eje -eje.

Solución

Dado que el eje de rotación es vertical, necesitamos convertir la función en una función de$y$ y convertir los$x$ -bounds a$y$ -bounds. Ya que$y=1/x$ define la curva, la reescribimos como$x=1/y$. El encuadernado$x=1$ corresponde al$y$ -bound$y=1$, y el bound$x=2$ corresponde al$y$ -bound$y=1/2$.

Así estamos rotando la curva$x=1/y$, de$y=1/2$ a$y=1$ alrededor del$y$ eje -para formar un sólido. La curva y el elemento diferencial de muestra se esbozan en la Figura$\PageIndex{5a}$, con un boceto completo del sólido en la Figura$\PageIndex{5b}$.

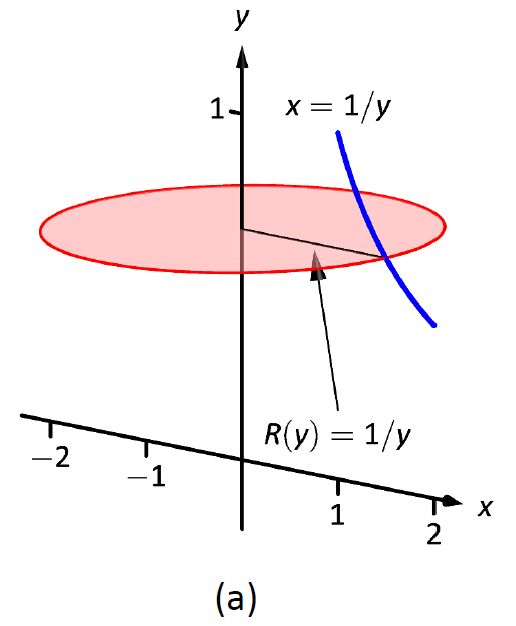
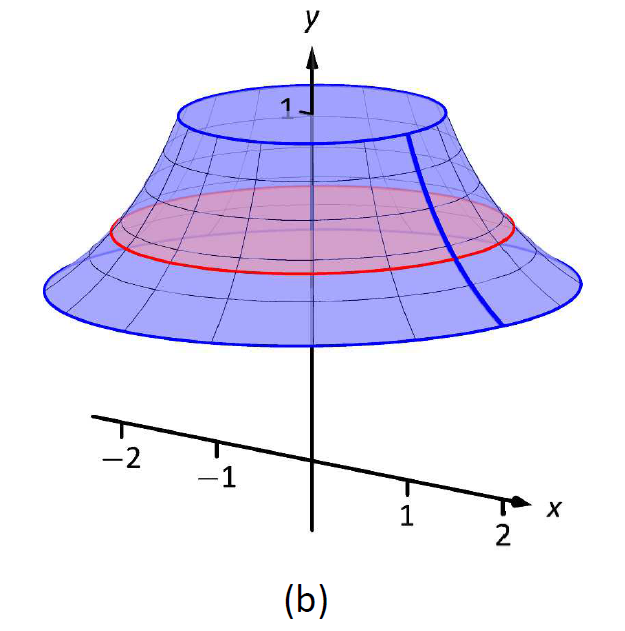
$7.2.5a.png$ $7.2.5b.png$

Figura$\PageIndex{5}$: Esbozo de un sólido en Ejemplo$\PageIndex{3}$.

Nos integramos para encontrar el volumen:

\[\begin{align}V &= \pi\int_{1/2}^1 \frac{1}{y^2}\ dy \\ &= -\frac{\pi}y\Big|_{1/2}^1 \\ &= \pi\ \text{units}^3. \end{align}\]

También podemos calcular el volumen de sólidos de revolución que tienen un agujero en el centro. El principio general es simple: computar el volumen del sólido independientemente del agujero, luego restar el volumen del agujero. Si el radio exterior del sólido es$R(x)$ y el radio interior (que define el agujero) es$r(x)$, entonces el volumen es

$$V =\ pi\ int_a^b R (x) ^2\ dx -\ pi\ int_a^b r (x) ^2\ dx =\ pi\ int_a^b\ izquierda (R (x) ^2-r (x) ^2\ derecha)\ dx.\]

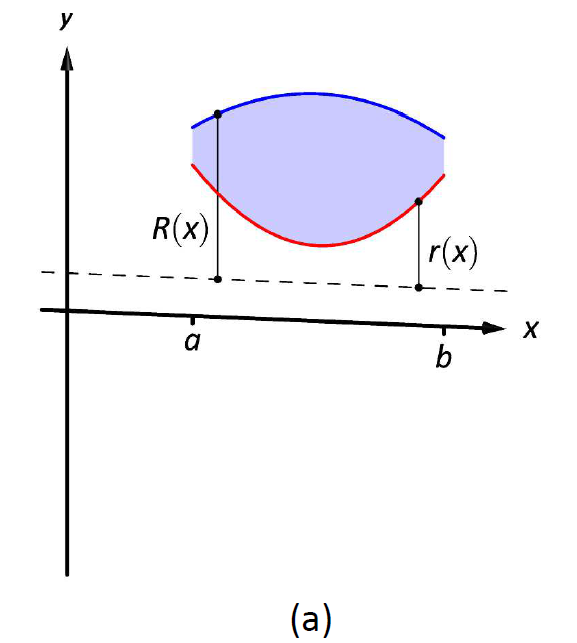
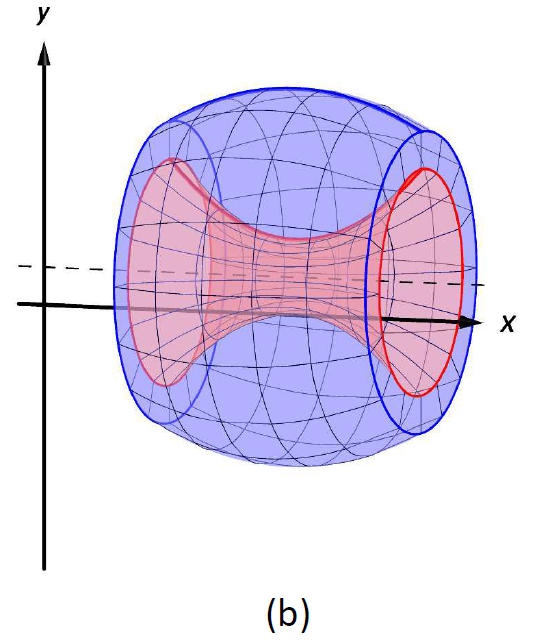
$7.2.6a.png$ $7.2.6b.png$

Figura$\PageIndex{6}$: Establecimiento del Método de Arandela; ver también Figura$\PageIndex{7}$.

Se puede generar un sólido de revolución con un agujero en el medio girando una región alrededor de un eje. Considere Figura$\PageIndex{6a}$, donde se esboza una región junto con un eje de rotación horizontal discontinua. Al rotar la región alrededor del eje, se forma un sólido como se esboza en la Figura$\PageIndex{6b}$. El exterior del sólido tiene radio$R(x)$, mientras que el interior tiene radio$r(x)$. Cada sección transversal de este sólido será una arandela (un disco con un agujero en el centro) como se esboza en la Figura$\PageIndex{6b}$. Esto nos lleva al Método de Arandela.

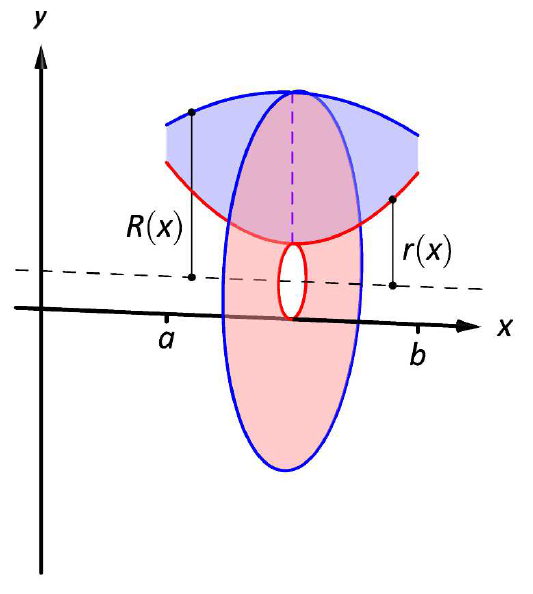
$7.2.7.png$

Figura$\PageIndex{7}$: Establecimiento del Método de Arandela; ver también Figura$\PageIndex{6}$.

Idea Clave 24: El Método de Arandela

Deje que una región delimitada por$y=f(x)$,$y=g(x)$,$x=a$ y$x=b$ se rote alrededor de un eje horizontal que no intersecta la región, formando un sólido. Cada sección transversal$x$ será una arandela con radio exterior$R(x)$ y radio interior$r(x)$. El volumen del sólido es

\[V = \pi\int_a^b \Big(R(x)^2-r(x)^2\Big)\ dx.\]

A pesar de que lo presentamos primero, el Método de Disco es solo un caso especial del Método de Arandela con un radio interior de$r(x)=0$.

Ejemplo$\PageIndex{4}$: Finding volume with the Washer Method

Encuentra el volumen del sólido formado rotando la región delimitada por$y=x^2-2x+2$ y$y=2x-1$ alrededor del$x$ eje.

Solución

Un boceto de la región ayudará, como se da en la Figura$\PageIndex{8a}$.

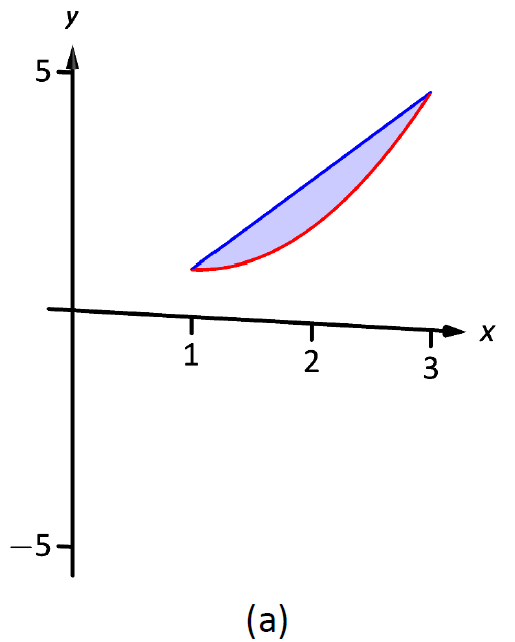
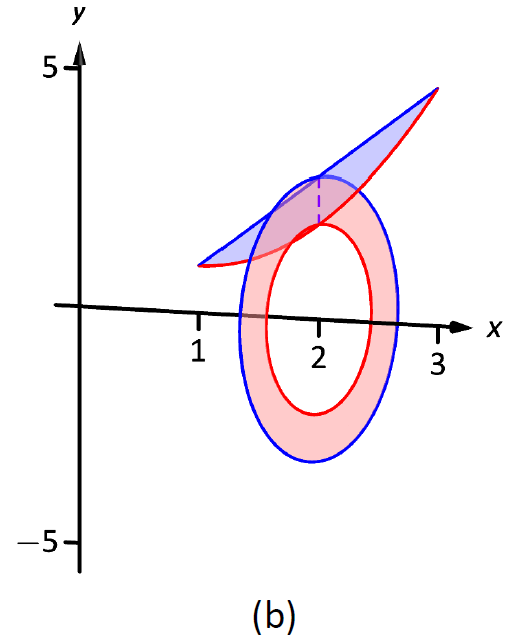
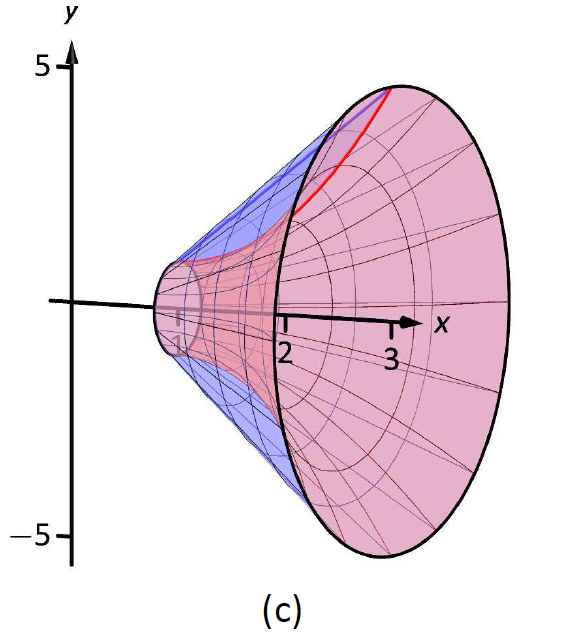
$7.2.8a.png$ $7.2.8b.png$ $7.2.8c.png$

Figura$\PageIndex{8}$: Esbozo del elemento diferencial y sólido en Ejemplo$\PageIndex{4}$.

Al girar alrededor del$x$ eje se producirán secciones transversales en forma de arandelas, como se muestra en la Figura$\PageIndex{8b}$; el sólido completo se muestra en la parte (c). El radio exterior de esta arandela es$R(x) = 2x+1$; el radio interior es$r(x) = x^2-2x+2$. Como la región está delimitada de$x=1$ a$x=3$, integramos de la siguiente manera para calcular el volumen.

\[\begin{align}V &= \pi\int_1^3 \Big((2x-1)^2-(x^2-2x+2)^2\Big)\ dx \\ &= \pi\int_1^3 \big(-x^4+4x^3-4x^2+4x-3\big)\ dx \\ &= \pi\Big[-\frac{1}{5}x^5+x^4-\frac43x^3+2x^2-3x\Big]\Big|_1^3 \\ &=\frac{104}{15}\pi \approx 21.78\ \text{units}^3.\end{align} \]

Al girar alrededor de un eje vertical, las funciones de radio exterior e interior deben ser funciones de$y$.

Ejemplo$\PageIndex{5}$: Finding volume with the Washer Method

Encuentra el volumen del sólido formado girando la región triangular con vértices en$(1,1)$,$(2,1)$ y$(2,3)$ alrededor del$y$ eje -eje.

Solución

La región triangular se esboza en la Figura$\PageIndex{9}$; el elemento diferencial se esboza en (b) y el sólido completo se dibuja en (c). Nos ayudan a establecer los radios exterior e interior. Dado que el eje de rotación es vertical, cada radio es una función de$y$.

El radio exterior$R(y)$ está formado por la línea que conecta$(2,1)$ y$(2,3)$; es una función constante, ya que independientemente del$y$ -valor la distancia desde la línea hasta el eje de rotación es 2. Así$R(y)=2$.

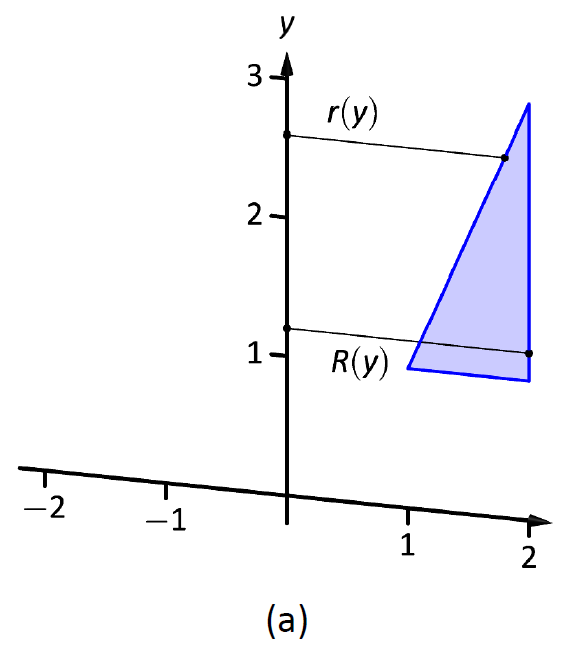
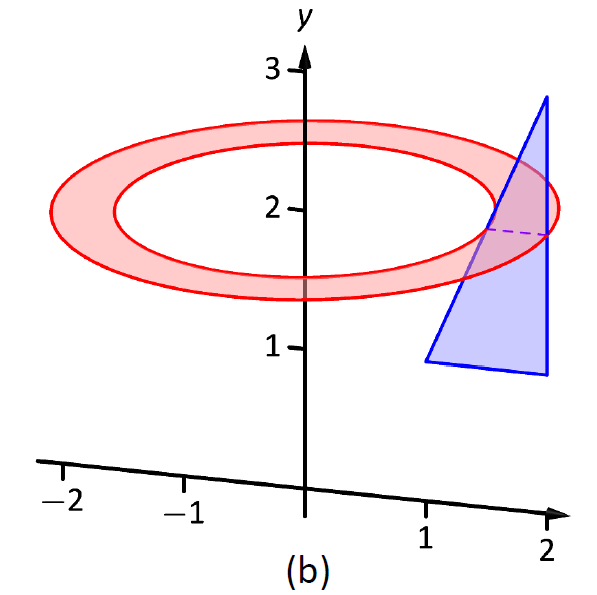
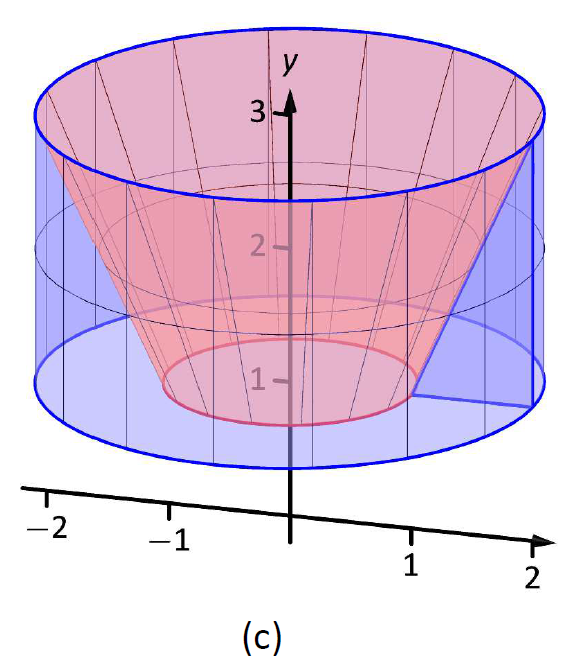
$7.2.9a.png$ $7.2.9b.png$ $7.2.9c.png$

Figura$\PageIndex{9}$: Esbozo del sólido en Ejemplo$\PageIndex{5}$.

El radio interior está formado por la línea que conecta$(1,1)$ y$(2,3)$. La ecuación de esta línea es$y=2x-1$, pero necesitamos referirnos a ella en función de$y$. Resolviendo para$x$ da$r(y) = \frac12(y+1)$.

Nos integramos sobre los$y$ límites de$y=1$ a$y=3$. Así el volumen es

\[\begin{align}V &= \pi\int_1^3\Big(2^2 - \big(\frac12(y+1)\big)^2\Big)\ dy \\ &= \pi\int_1^3\Big(-\frac14y^2-\frac12y+\frac{15}4\Big)\ dy \\ &= \pi\Big[-\frac1{12}y^3-\frac14y^2+\frac{15}4y\Big]\Big|_1^3\\ &= \frac{10}3\pi \approx 10.47\ \text{units}^3.\end{align}\]

Esta sección introdujo una nueva aplicación de la integral definitiva. Nuestra visión predeterminada de la integral definida es que da “el área bajo la curva”. Sin embargo, podemos establecer integrales definidas que representen otras cantidades; en esta sección, calculamos el volumen.

El objetivo final de esta sección no es computar volúmenes de sólidos. Eso puede ser útil, pero lo que es más útil es la comprensión de este principio básico del cálculo integral, esbozado en la Idea Clave 24: para encontrar el valor exacto de alguna cantidad,

comenzamos con una aproximación (en esta sección, rebanamos el sólido y aproximamos el volumen de cada rebanada),
luego hacer la aproximación mejor refinando nuestra aproximación original (es decir, usar más rebanadas),
luego usar límites para establecer una integral definida que dé el valor exacto.

Practicamos este principio en la siguiente sección donde encontramos volúmenes cortando sólidos de una manera diferente.