11.1: Funciones Vector-Valoradas

Estamos muy familiarizados con las funciones de valor real, es decir, funciones cuya salida es un número real. Esta sección introduce funciones con valores vectoriales, funciones cuya salida es un vector.

Definición\(\PageIndex{1}\): Vector-Valued Functions

Una función de valor vectorial es una función de la forma

\[\vecs r(t) = \langle\, f(t),g(t)\,\rangle\]

o

\[\vecs r(t) = \langle \,f(t),g(t),h(t)\,\rangle,\]

donde\(f\),\(g\) y\(h\) son funciones reales valoradas.

El dominio de\(\vecs r\) es el conjunto de todos los valores de\(t\) para los que\(\vecs r(t)\) se define. El rango de\(\vecs r\) es el conjunto de todos los vectores de salida posibles\(\vecs r(t)\).

Evaluación y Gráfica de Funciones Valoradas por Vector

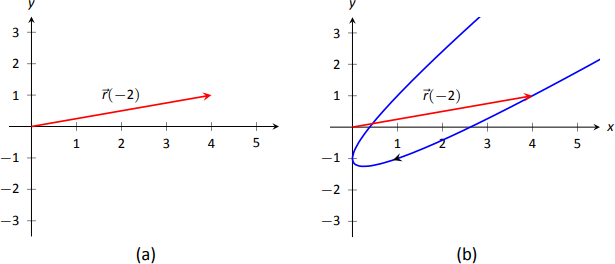
Evaluar una función valorada por vector a un valor específico de\(t\) es sencillo; simplemente evalúe cada función componente a ese valor de\(t\). Por ejemplo, si\(\vecs r(t) = \langle t^2,t^2+t-1\rangle\), entonces\(\vecs r(-2) = \langle 4,1\rangle\). Podemos bosquejar este vector, como se hace en la Figura\(\PageIndex{1a}\). Sin embargo, trazar muchos vectores es engorroso, por lo que generalmente no dibujamos todo el vector sino solo el punto terminal. El gráfico de una función vectorizada es el conjunto de todos los puntos terminales de\(\vecs r(t)\), donde el punto inicial de cada vector es siempre el origen. En la Figura\(\PageIndex{1b}\) esbozamos la gráfica de\(\vecs r\); podemos indicar puntos individuales en la gráfica con su respectivo vector, como se muestra.

Figura\(\PageIndex{1}\): Croquizar la gráfica de una función de valor vectorial.

Las funciones con valores vectoriales están estrechamente relacionadas con las ecuaciones paramétricas de las gráficas. Mientras que en ambos métodos trazamos puntos\(\big(x(t), y(t)\big)\) o\(\big(x(t),y(t),z(t)\big)\) para producir una gráfica, en el contexto de las funciones vectorizadas cada punto representa un vector. Las implicaciones de esto se concretarán más plenamente en la siguiente sección a medida que aplicemos ideas de cálculo a estas funciones.

Ejemplo\(\PageIndex{1}\): Graphing vector-valued functions

Gráfica\( \vecs r(t) = \langle t^3-t, \dfrac{1}{t^2+1}\rangle\), para\(-2\leq t\leq 2\). Sketch\(\vecs r(-1)\) y\(\vecs r(2)\).

Solución

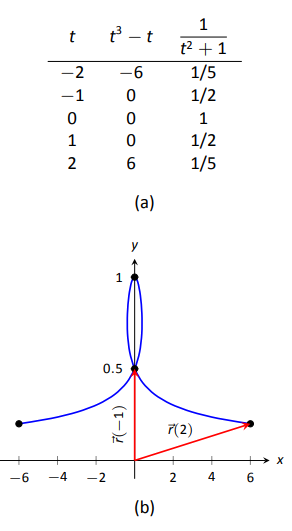
Comenzamos haciendo una tabla de\(t\),\(x\) y\(y\) valores como se muestra en la Figura\(\PageIndex{1a}\). Trazar estos puntos da una indicación de cómo se ve la gráfica. En la Figura\(\PageIndex{1b}\), indicamos estos puntos y bosquejamos la gráfica completa. También destacamos\(\vecs r(-1)\) y\(\vecs r(2)\) en la gráfica.

Figura\(\PageIndex{2}\): Esbozo de la función vectorizada del Ejemplo 11.1.1

Ejemplo\(\PageIndex{2}\): Graphing vector-valued functions.

Gráfica\(\vecs r(t) = \langle \cos t,\sin t,t\rangle\) para\(0\leq t\leq 4\pi\).

Solución

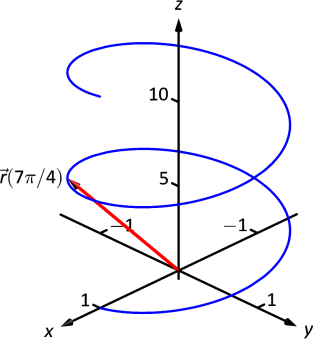
De nuevo podemos trazar puntos, pero la consideración cuidadosa de esta función es muy reveladora. Ignorando momentáneamente el tercer componente, vemos que\(y\) los componentes\(x\) y trazan un círculo de radio 1 centrado en el origen. Al notar que el\(z\) componente es\(t\), vemos que a medida que la gráfica se enrolla alrededor del\(z\) eje -eje, también está aumentando a un ritmo constante en la\(z\) dirección positiva, formando una espiral. Esto se grafica en la Figura\(\PageIndex{3}\). En la gráfica\(\vecs r(7\pi/4)\approx (0.707,-0.707,5.498) \) se resalta para ayudarnos a entender la gráfica.

Figura\(\PageIndex{3}\): Visualización de una función vectorizada, y su derivada en un punto.

Álgebra de Funciones Vector-Valoradas

Definición\(\PageIndex{2}\): Operations on Vector-Valued Functions

Dejar\(\vecs r_1(t)=\langle f_1(t),g_1(t)\rangle\) y\(\vecs r_2(t)=\langle f_2(t),g_2(t)\rangle\) ser funciones vectorizadas en\(\mathbb{R}^2\) y dejar\(c\) ser un escalar. Entonces:

1. \(\vecs r_1(t) \pm \vecs r_2(t) = \langle\, f_1(t)\pm f_2(t),g_1(t)\pm g_2(t)\,\rangle\).
2. \(c\vecs r_1(t) = \langle\, cf_1(t),cg_1(t)\,\rangle\).

Una definición similar se mantiene para las funciones con valores vectoriales en\(\mathbb{R}^3\).

Esta definición establece que sumamos, restamos y escalamos funciones con valor vectorial por componentes. Combinar funciones con valores vectoriales de esta manera puede ser muy útil (así como crear gráficas interesantes).

Ejemplo\(\PageIndex{3}\): Adding and scaling vector-valued functions.

Vamos\(\vecs r_1(t) = \langle\,0.2t,0.3t\,\rangle\),\(\vecs r_2(t) = \langle\,\cos t,\sin t\,\rangle\) y\(\vecs r(t) = \vecs r_1(t)+\vecs r_2(t)\). Gráfica\(\vecs r_1(t)\),\(\vecs r_2(t)\),\(\vecs r(t)\) y\(5\vecs r(t)\) sucesivamente\(-10\leq t\leq10\).

Solución

Podemos graficar\(\vecs r_1\) y\(\vecs r_2\) fácilmente trazando puntos (o simplemente usando tecnología). Pensemos en cada uno por un momento para entender mejor cómo funcionan las funciones con valores vectoriales.

Podemos reescribir\(\vecs r_1(t) = \langle\, 0.2t,0.3t\,\rangle\) como\( \vecs r_1(t) = t\langle 0.2,0.3\rangle\). Es decir, la función\(\vecs r_1\) escala el vector\(\langle 0.2,0.3\rangle\) por\(t\). Esta escala de un vector produce una línea en la dirección de\(\langle 0.2,0.3\rangle\).

Estamos familiarizados con\(\vecs r_2(t) = \langle\, \cos t,\sin t\,\rangle\); traza un círculo, centrado en el origen, de radio 1. \(\PageIndex{4a}\)Gráficas de figuras\(\vecs r_1(t)\) y\(\vecs r_2(t)\).

Sumando\(\vecs r_1(t)\) a\(\vecs r_2(t)\) produce\(\vecs r(t) = \langle\,\cos t + 0.2t,\sin t+0.3t\,\rangle\), graficado en la Figura\(\PageIndex{4b}\). El movimiento lineal de la línea se combina con el círculo para crear bucles que se mueven en la dirección de\(\langle 0.2,0.3\rangle\). (Animamos al lector a experimentar cambiando\(\vecs r_1(t)\) a\(\langle 2t,3t\rangle\), etc., y observar los efectos en los bucles.)

Figura\(\PageIndex{4}\): Graficando las funciones en Ejemplo\(\PageIndex{3}\)

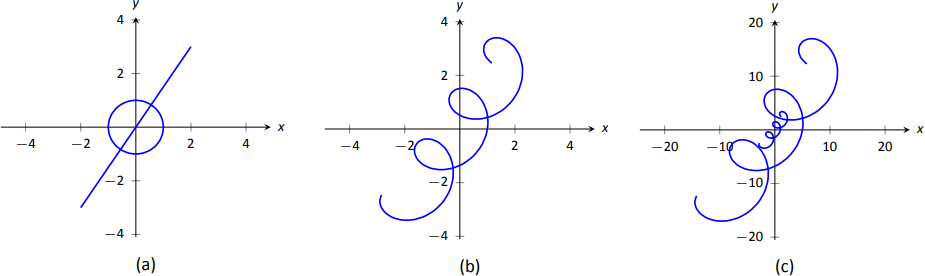
Multiplicando\(\vecs r(t)\) por 5 escalas la función por 5, produciendo\(5\vecs r(t) = \langle 5\cos t+1,5\sin t+1.5\rangle\), que se grafica en la Figura\(\PageIndex{4c}\) junto con\(\vecs r(t)\). La nueva función es “5 veces mayor” que\(\vecs r(t)\). Observe cómo la gráfica de\(5\vecs r(t)\) en (c) se ve idéntica a la gráfica de\(\vecs r(t)\) in\((b)\). Esto se debe a que los\(y\) límites\(x\) y de la trama en\((c)\) son exactamente 5 veces mayores que los límites en (b).

Ejemplo\(\PageIndex{4}\): Adding and scaling vector-valued functions.

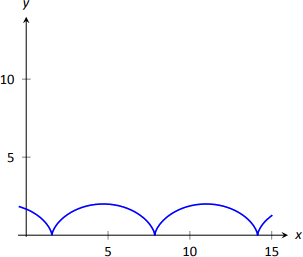
Un cicloide es una gráfica trazada por un punto\(p\) en un círculo rodante, como se muestra en la Figura\(\PageIndex{5}\). Encuentra una ecuación que describa el cicloide, donde el círculo tiene radio 1.

Figura\(\PageIndex{5}\): Rastreo de un cicloide.

Solución

Este problema no es muy difícil si lo abordamos de manera inteligente. Comenzamos dejando\(\vecs p(t)\) describir la posición del punto\(p\) en el círculo, donde el círculo está centrado en el origen y solo gira en sentido horario (es decir, no rueda). Esto es relativamente simple dadas nuestras experiencias previas con ecuaciones paramétricas;\(\vecs p(t) = \langle \cos t, -\sin t\rangle\).

Ahora queremos que ruede el círculo. Representamos esto dejando\(\vecs c(t)\) representar la ubicación del centro del círculo. Debe quedar claro que el\(y\) componente de\(\vecs c(t)\) debe ser 1; el centro del círculo siempre va a ser 1 si rueda sobre una superficie horizontal.

El\(x\) componente de\(\vecs c(t)\) es una función lineal de\(t\):\(f(t) = mt\) para algunos escalar\(m\). Cuando\(t=0\),\(f(t) = 0\) (el círculo comienza centrado en el\(y\) eje -eje). Cuando\(t=2\pi\), el círculo ha hecho una revolución completa, recorriendo una distancia igual a su circunferencia, que también es\(2\pi\). Esto nos da un punto en nuestra línea\(f(t) = mt\), el punto\((2\pi, 2\pi)\). Debe quedar claro que\(m=1\) y\(f(t) = t\). Entonces\(\vecs c(t) = \langle t, 1\rangle\).

Ahora combinamos\(\vecs p\) y\(\vecs c\) juntos para formar la ecuación del cicloide:

\[\vecs r(t) = \vecs p(t) + \vecs c(t) = \langle \cos t+ t,-\sin t+1\rangle, \nonumber\]

que se grafica en la Figura\(\PageIndex{6}\).

Figura\(\PageIndex{6}\): El cicloide en el Ejemplo\(\PageIndex{4}\).

Desplazamiento

A menudo\(\vecs r(t)\) se usa una función de valor vectorial para describir la posición de un objeto en movimiento en el momento\(t\). A\(t=t_0\), el objeto está en\(\vecs r(t_0)\); a\(t=t_1\), el objeto está en\(\vecs r(t_1)\). Conocer las localizaciones\(\vecs r(t_0)\) y no\(\vecs r(t_1)\) dar ninguna indicación del camino tomado entre ellas, pero muchas veces solo nos importa la diferencia de las localizaciones,\(\vecs r(t_1)-\vecs r(t_0)\), el desplazamiento.

Definición\(\PageIndex{3}\): Displacement

Dejar\(\vecs r(t)\) ser una función vectorizada y dejar\(t_0<t_1\) ser valores en el dominio. El desplazamiento \(\vecs d\)de\(\vecs r\), de\(t=t_0\) a\(t=t_1\), es\[\vecs d=\vecs r(t_1)-\vecs r(t_0).\]

Cuando se dibuja el vector de desplazamiento con punto inicial en\(\vecs r(t_0)\), su punto terminal es\(\vecs r(t_1)\). Pensamos en ello como el vector que apunta desde una posición inicial a una posición final.

Ejemplo\(\PageIndex{5}\): Finding and graphing displacement vectors

Vamos\(\vecs r(t) = \langle \cos (\dfrac{\pi}{2}t),\sin (\dfrac{\pi}2 t)\rangle\). Gráfica\(\vecs r(t)\) sobre\(-1\leq t\leq 1\), y encuentra el desplazamiento de\(\vecs r(t)\) en este intervalo.

Solución

La función\(\vecs r(t)\) traza el círculo unitario, aunque a una velocidad diferente a la\(\langle \cos t,\sin t\rangle\) parametrización “habitual”. En\(t_0=-1\), tenemos\(\vecs r(t_0) = \langle 0,-1\rangle\); en\(t_1=1\), tenemos\(\vecs r(t_1) = \langle 0,1\rangle\). El desplazamiento de\(\vecs r(t)\) on\([-1,1]\) es así

\[\vecs d = \langle 0,1\rangle - \langle 0,-1\rangle = \langle 0,2\rangle. \nonumber\]

Figura\(\PageIndex{7}\): Graficando el desplazamiento de una función de posición en Ejemplo\(\PageIndex{5}\).

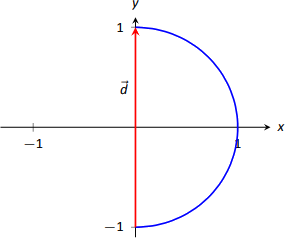
Una gráfica de\(\vecs r(t)\) on\([-1,1]\) se da en la Figura\(\PageIndex{7}\), junto con el vector de desplazamiento\(\vecs d\) en este intervalo.

Medir el desplazamiento nos hace contemplar conceptos relacionados, pero muy diferentes. Considerando la trayectoria semicircular que\(\PageIndex{5}\) tomó el objeto en Ejemplo, podemos verificar rápidamente que el objeto terminó a una distancia de 2 unidades desde su ubicación inicial. Es decir, podemos calcular\(\norm{d} = 2\). Sin embargo, medir la distancia desde el punto de partida es diferente de medir la distancia recorrida. Al ser un semicírculo, podemos medir la distancia recorrida por este objeto como\(\pi\approx 3.14\) unidades. Conocer la distancia desde el punto de partida nos permite calcular la tasa promedio de cambio.

Definición\(\PageIndex{4}\): Average Rate of Change

Dejar\(\vecs r(t)\) ser una función de valor vectorial, donde cada una de sus funciones componentes es continua en su dominio, y let\(t_0<t_1\). La tasa promedio de cambio de\(\vecs r(t)\) on\([t_0,t_1]\) es

\[\text{average rate of change} = \dfrac{\vecs r(t_1) - \vecs r(t_0)}{t_1-t_0}.\]

Ejemplo\(\PageIndex{6}\): Average rate of change

Que\(\vecs r(t) = \langle \cos(\dfrac{\pi}2t),\sin(\dfrac{\pi}2t)\rangle\) como en el Ejemplo 11.1.5. Encuentra la tasa promedio de cambio\(\vecs r(t)\) de una\([-1,1]\) y otra\([-1,5]\).

Solución

Calculamos en Ejemplo\(\PageIndex{5}\) que el desplazamiento de\(\vecs r(t)\) on\([-1,1]\) fue\(\vecs d = \langle 0,2\rangle\). Así, la tasa promedio de cambio de\(\vecs r(t)\) on\([-1,1]\) es:

\[\dfrac{\vecs r(1) -\vecs r(-1)}{1-(-1)} = \dfrac{\langle 0,2\rangle}{2} = \langle 0,1\rangle. \nonumber\]

Interpretamos esto de la siguiente manera: el objeto siguió un camino semicircular, es decir, se movió hacia la derecha luego se movió de nuevo a la izquierda, mientras que trepaba lentamente, luego rápidamente, luego lentamente otra vez. En promedio, sin embargo, progresó hacia arriba a un ritmo constante de\(\langle 0,1\rangle\) por unidad de tiempo.

Podemos ver rápidamente que el desplazamiento encendido\([-1,5]\) es el mismo que el encendido\([-1,1]\), entonces\(\vecs d = \langle 0,2\rangle\). La tasa promedio de cambio es diferente, aunque:

\[\dfrac{\vecs r(5)-\vecs r(-1)}{5-(-1)} = \dfrac{\langle 0,2\rangle}{6} = \langle 0,1/3\rangle. \nonumber\]

Al tomar “3 veces más tiempo” llegar al mismo lugar, esta tasa promedio de cambio en\([-1,5]\) es\(1/3\) la tasa promedio de cambio en\([-1,1]\).

Consideramos las tasas promedio de cambio en las Secciones 1.1 y 2.1 mientras estudiamos límites y derivados. Lo mismo es cierto aquí; en la siguiente sección aplicamos conceptos de cálculo a las funciones vectoriales a medida que encontramos límites, derivadas e integrales. Comprender la tasa promedio de cambio nos dará una comprensión de la derivada; el desplazamiento nos da una aplicación de integración.

Colaboradores y Atribuciones

• Template:ContribApexCalc