11.3: El cálculo del movimiento

Un uso común de las funciones con valores vectoriales es describir el movimiento de un objeto en el plano o en el espacio. Una función de posición\(\vecs r(t)\) da la posición de un objeto a la vez\(t\). Esta sección explora cómo se utilizan derivados e integrales para estudiar el movimiento descrito por dicha función.

Definición 73: Velocidad, Velocidad y Aceleración

Dejar\(\vecs r(t)\) ser una función de posición en\(\mathbb{R}^2\) o\(\mathbb{R}^3\).

• La velocidad, denotada\(\vecs v(t)\), es la velocidad instantánea de cambio de posición; es decir,

\[\vecs v(t) = \vecs r^\prime (t).\]

• La velocidad es la magnitud de la velocidad,

\[ \text{speed} = \norm{\vecs v(t)}.\]

• La aceleración, denotada\(\vecs a(t)\), es la velocidad instantánea de cambio de velocidad; es decir,

\[\vecs a(t) = \vecs v\,'(t) = \vecs r^{\prime\prime}(t).\]

Ejemplo\(\PageIndex{1}\): Finding velocity and acceleration

Un objeto se mueve con función de posición\(\vecs r(t) = \langle t^2-t,t^2+t\rangle\),\(-3\leq t\leq 3\), donde las distancias se miden en pies y el tiempo se mide en segundos.

1. Encontrar\(\vecs v (t)\) y\(\vecs a (t)\).
2. Sketch\(\vecs r (t)\); plot\(\vecs v(-1)\)\(\vecs a(-1)\),\(\vecs a(1)\),\(\vecs v(1)\) y, cada uno con su punto inicial en su punto correspondiente en la gráfica de\(\vecs r (t)\).
3. ¿Cuándo se minimiza la velocidad del objeto?

Solución

1. Tomando derivados, encontramos\[\vecs v (t) = \vecs r^\prime (t) =\langle 2t-1,2t+1\rangle \nonumber\] y\[\quad \vecs a (t) = \vecs r^{\prime\prime}(t) = \langle 2,2\rangle. \nonumber\] Notamos que la aceleración es constante.
   
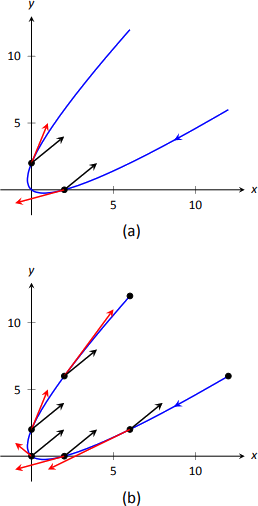
2. \(\vecs v(-1) = \langle -3,-1\rangle\),\(\vecs a(-1) = \langle 2,2\rangle\);\(\vecs v(1) = \langle 1,3\rangle\),\(\vecs a(1) = \langle 2,2\rangle\). Estos se trazan con\(\vecs r (t)\) en la Figura\(\PageIndex{1a}\).
   Podemos pensar en la aceleración como “tirar” del vector de velocidad en cierta dirección. At\(t=-1\), el vector de velocidad apunta hacia abajo y hacia la izquierda; at\(t=1\), el vector de velocidad ha sido tirado en la\(\langle 2,2\rangle\) dirección y ahora apunta hacia arriba y hacia la derecha. En la Figura 11.15 (b) trazamos más vectores de velocidad/aceleración, dejando más claro el efecto que tiene la aceleración sobre la velocidad.
   Ya que\(\vecs a (t)\) es constante en este ejemplo, a medida\(t\) que crece grande\(\vecs v (t)\) se vuelve casi paralelo a\(\vecs a (t)\). Por ejemplo, cuando\(t=10\),\(\vecs v(10) = \langle 19,21\rangle\), que es casi paralelo a\(\langle 2,2\rangle\).
3. La velocidad del objeto viene dada por\[\norm{\vecs v (t)} = \sqrt{(2t-1)^2+(2t+1)^2} =\sqrt{8t^2+2}.\] Para encontrar la velocidad mínima, podríamos aplicar técnicas de cálculo (como establecer la derivada igual a 0 y resolver para\(t\), etc.) pero podemos encontrarla por inspección. Dentro de la raíz cuadrada tenemos una cuadrática que se minimiza cuando\(t=0\). Así, la velocidad se minimiza a\(t=0\), con una velocidad de\(\sqrt{2}\) pies/s.
   
   La gráfica en la Figura\(\PageIndex{1b}\) también implica que la velocidad se minimiza aquí. Los puntos rellenos en la gráfica se ubican en valores enteros de\(t\) entre\(-3\) y 3. Los puntos que están muy separados implican que el objeto viajó lejos en 1 segundo, lo que indica alta velocidad; los puntos que están muy juntos implican que el objeto no viajó lejos en 1 segundo, lo que indica una velocidad baja. Los puntos están más cerca juntos\(t=0\), lo que implica que la velocidad se minimiza cerca de ese valor.

Figura\(\PageIndex{1}\): Graficando la posición, velocidad y aceleración de un objeto en el Ejemplo 11.3.1

Ejemplo\(\PageIndex{2}\): Analyzing Motion

Dos objetos siguen una trayectoria idéntica a diferentes velocidades en\([-1,1]\). La función de posición para el Objeto 1 es\(\vecs r_1(t) = \langle t, t^2\rangle\); la función de posición para el Objeto 2 es\(\vecs r_2(t) = \langle t^3, t^6\rangle\), donde las distancias se miden en pies y el tiempo se mide en segundos. Compara la velocidad, velocidad y aceleración de los dos objetos en la trayectoria.

Solución

Comenzamos calculando la función de velocidad y aceleración para cada objeto:

\ [\ begin {align*}
\ vecs v_1 (t) &=\ langle 1,2t\ rangle &\ vecs v_2 (t) &=\ langle 3t^2,6t^5\ rangle\\ [4pt]
\ vecs a_1 (t) &=\ langle 0,2\ rangle &\ vecs a_2 (t) &=\ langle 6t,30t^4\ rangle
\ final {alinear*}\]

Inmediatamente vemos que el Objeto 1 tiene una aceleración constante, mientras que el Objeto 2 no.

At\(t=-1\), tenemos\(\vecs v_1(-1) = \langle 1,-2\rangle\) y\(\vecs v_2(-1) = \langle 3,-6\rangle\); la velocidad del Objeto 2 es tres veces mayor que la del Objeto 1 y así se deduce que la velocidad del Objeto 2 es tres veces la del Objeto 1 (\(3\sqrt{5}\)ft/s en comparación con\(\sqrt{5}\) ft/s.)

Figura\(\PageIndex{2}\): Trazar vectores de velocidad y aceleración para el Objeto 1 en el Ejemplo 11.3.2

A\(t=0\), ¡la velocidad del Objeto 1 es\(\vecs v(1) = \langle 1,0\rangle\) y la velocidad del Objeto 2 es\(\vecs 0\)! Esto nos dice que Object 2 llega a una parada completa en\(t=0\).

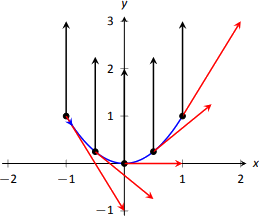
En la Figura\(\PageIndex{2}\), vemos los vectores de velocidad y aceleración para el Objeto 1 trazados para\(t=-1, -1/2, 0, 1/2\) y\(t=1\). Observe nuevamente cómo el vector de aceleración constante parece “tirar” del vector de velocidad de apuntar hacia abajo, de derecha a arriba, derecha. Podríamos trazar la imagen análoga para el Objeto 2, pero los vectores de velocidad y aceleración son bastante grandes (\(\vecs a_2(-1) = \langle -6,30\rangle\)!)

En cambio, simplemente trazamos las ubicaciones del Objeto 1 y 2 en intervalos\(1/10^{\text{th}}\) de un segundo, que se muestran en la Figura\(\PageIndex{3a}\) y\(\PageIndex{3b}\). Observe cómo los\(x\) valores -del Objeto 1 aumentan a un ritmo constante. Esto se debe a que el\(x\) -componente de\(\vecs a(t)\) es 0; no hay aceleración en el\(x\) -componente. Los puntos no están espaciados uniformemente; el objeto se mueve más rápido cerca\(t=-1\) y\(t=1\) que cerca\(t=0\).

Figura\(\PageIndex{3}\): Comparando las posiciones de los Objetos 1 y 2 en el Ejemplo 11.3.2

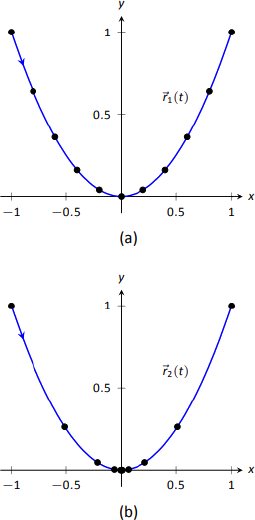
En la Figura\(\PageIndex{3b}\), vemos los puntos trazados para el Objeto 2. Observe el gran cambio de posición de\(t=-1\) a\(t=-0.9\); el objeto comienza a moverse muy rápidamente. Sin embargo, se ralentiza considerablemente cuando se acerca al origen, y llega a una parada completa en\(t=0\). Si bien parece que hay 3 puntos cerca del origen, en realidad hay 5 puntos ahí.

Dado que los objetos comienzan y terminan en la misma ubicación, los tienen el mismo desplazamiento. Desde que comienzan y terminan al mismo tiempo, con el mismo desplazamiento, tienen que tienen la misma tasa promedio de cambio (es decir, tienen la misma velocidad promedio). Ya que siguen el mismo camino, tienen la misma distancia recorrida. A pesar de que estas tres medidas son las mismas, los objetos obviamente recorren el camino de maneras muy diferentes.

Ejemplo\(\PageIndex{3}\): Analyzing the motion of a whirling ball on a string

Un joven gira una pelota, unida a una cuerda, por encima de su cabeza en un círculo en sentido antihorario. El balón sigue una trayectoria circular y hace 2 revoluciones por segundo. La cuerda tiene una longitud de 2ft.

1. Encuentra la función de posición\(\vecs r(t)\) que describe esta situación.
2. Encuentra la aceleración de la pelota y deriva una interpretación física de la misma.
3. Un árbol se encuentra a 10 pies frente al niño. ¿A qué\(t\) -valores debe el chico soltar la cuerda para que la pelota golpee al árbol?

Solución

1. La bola da un giro en círculo. Dado que la cuerda mide 2 pies de largo, el radio del círculo es 2. La función de posición\(\vecs r (t)= \langle 2\cos t, 2\sin t\rangle\) describe un círculo con radio 2, centrado en el origen, pero hace una revolución completa cada\(2\pi\) segundo, no dos revoluciones por segundo. Modificamos el periodo de las funciones trigonométricas para que sea 1/2 multiplicando\(t\) por\(4\pi\). La función de posición final es así\[\vecs r (t) = \langle 2\cos (4\pi t), 2\sin (4\pi t)\rangle.\] (Trazar esto\(0\leq t\leq 1/2\) para verificar que se realiza una revolución en 1/2 segundo.)
2. Para encontrar\(\vecs a (t)\), derivamos\(\vecs r (t)\) dos veces. \[\begin{align*}\vecs v (t) = \vecs r^\prime (t) &= \langle -8\pi \sin (4\pi t), 8\pi \cos (4\pi t)\rangle\\[4pt] \vecs a (t) =\vecs r^{\prime\prime}(t) &= \langle -32\pi^2 \cos (4\pi t), -32\pi^2 \sin (4\pi t) \rangle \\[4pt]&= -32\pi^2\langle \cos (4\pi t), \sin (4\pi t)\rangle.\end{align*}\]
   
   Observe cómo\(\vecs a (t)\) es paralelo a\(\vecs r (t)\), pero tiene una magnitud diferente y apunta en la dirección opuesta. ¿Por qué es esto?
   
   Recordemos la ecuación clásica de la física, “\(\times\)Aceleración de\(=\) masa de fuerza”. Una fuerza que actúa sobre una masa induce la aceleración (es decir, la masa se mueve); la aceleración que actúa sobre una masa induce una fuerza (la gravedad le da a nuestra masa un peso). Así, la fuerza y la aceleración están estrechamente relacionadas. Una pelota en movimiento “quiere” viajar en línea recta. ¿Por qué la pelota en nuestro ejemplo se mueve en círculo? Se sujeta a la mano del niño por una cuerda. La cuerda aplica una fuerza a la pelota, afectando su movimiento: la cuerda acelera la pelota. Esto no es aceleración en el sentido de “viaja más rápido”; más bien, esta aceleración está cambiando la velocidad de la pelota. ¿En qué dirección se está aplicando esta fuerza/aceleración? En la dirección de la cuerda, hacia la mano del niño.
   
   La magnitud de la aceleración está relacionada con la velocidad a la que se desplaza la pelota. Una bola que da vueltas rápidamente está cambiando rápidamente de dirección/velocidad. Cuando la velocidad está cambiando rápidamente, la aceleración debe ser “grande”.
   
3. Cuando el niño suelta la cuerda, la cuerda ya no aplica una fuerza a la pelota, lo que significa que la aceleración es\(\vecs 0\) y la pelota ahora puede moverse en línea recta en la dirección de\(\vecs v(t)\).
   
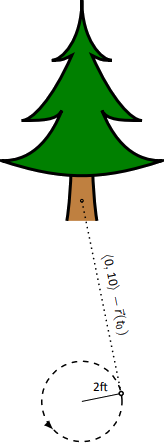
   Deja que\(t=t_0\) sea el momento en que el chico suelte la cuerda. El balón estará en\(\vecs r(t_0)\), viajando en dirección a\(\vecs v(t_0)\). Queremos encontrar para\(t_0\) que esta línea contenga el punto\((0,10)\) (ya que el árbol es de 10 pies directamente frente al niño).
   
   Hay muchas maneras de encontrar este valor de tiempo. Elegimos uno que sea relativamente simple computacionalmente. Como se muestra en la Figura\(\PageIndex{4}\), el vector desde el punto de liberación hasta el árbol es\(\langle 0,10\rangle - \vecs r(t_0)\). Este segmento de línea es tangente al círculo, lo que significa que también es perpendicular a\(\vecs r(t_0)\) sí mismo, por lo que su producto de punto es 0. \[ \begin{align*}\vecs r(t_0) \cdot \big(\langle 0,10\rangle - \vecs r(t_0)\big) &=0\\[4pt] \langle 2\cos (4\pi t_0), 2\sin (4\pi t_0)\rangle \cdot \langle -2\cos(4\pi t_0),10-2\sin (4\pi t_0)\rangle &=0\\[4pt]-4\cos^2(4\pi t_0) + 20\sin (4\pi t_0)-4\sin^2(4\pi t_0) &= 0\\[4pt]20\sin (4\pi t_0) - 4 &=0\\[4pt] \sin (4\pi t_0) &=1/5\\[4pt]4\pi t_0 &= \sin^{-1}(1/5)\\[4pt]4\pi t_0 &\approx 0.2 + 2\pi n, \end{align*}\]donde\(n\) es un entero. Resolviendo porque\(t_0\) tenemos:\[t_0 \approx 0.016 + n/2\nonumber\] Esta es una fórmula maravillosa. Cada 1/2 segundo después de\(t=0.016\) s el niño puede soltar la cuerda (ya que la pelota hace 2 revoluciones por segundo, tiene dos oportunidades cada segundo para liberar la pelota).

Figura\(\PageIndex{4}\): Modelado del vuelo de una pelota en el Ejemplo 11.3.3

Ejemplo\(\PageIndex{4}\): Analyzing motion in space

Un objeto se mueve en espiral con función de posición\(\vecs r (t) = \langle \cos t, \sin t, t\rangle\), donde las distancias se miden en metros y el tiempo es en minutos. Describir la velocidad y aceleración del objeto en el momento\(t\).

Solución
Con\(\vecs r (t) = \langle \cos t,\sin t, t\rangle\), contamos con:

\ [\ begin {align*}
\ vecs v (t) &=\ langle -\ sin t,\ cos t, 1\ rangle\ quad\ text {y}\\ [4pt]
\ vecs a (t) &=\ langle -\ cos t, -\ sin t, 0\ rangle.
\ end {alinear*}\]

La velocidad del objeto es\(\norm{\vecs v (t)} = \sqrt{(-\sin t)^2+\cos^2t+1} = \sqrt{2}\) m/min; se mueve a una velocidad constante. Tenga en cuenta que el objeto no acelera en la\(z\) dirección -sino que se mueve hacia arriba a una velocidad constante de 1m/min.

Los objetos de los Ejemplos 11.3.3 y 11.3.4 viajaron a una velocidad constante. Es decir,\(\norm{\vecs v (t)} = c\) para alguna constante\(c\). Recordemos el teorema 93, que establece que si una función vector—valorada\(\vecs r (t)\)\ tiene longitud constante, entonces\(\vecs r (t)\)\ es perpendicular a su derivada:\(\vecs r (t)\cdot\vecs r^\prime (t) = 0\). En estos ejemplos, la función de velocidad tiene longitud constante, por lo tanto podemos concluir que la velocidad es perpendicular a la aceleración:\(\vecs v (t)cdot\vecs a (t) = 0\). Un chequeo rápido lo verifica.

Hay una comprensión intuitiva de esto. Si la aceleración es paralela a la velocidad, entonces solo está afectando la velocidad del objeto; no cambia la dirección de desplazamiento. (Por ejemplo, considere una piedra caída. La aceleración y la velocidad son paralelas, rectas hacia abajo, y la dirección de la velocidad nunca cambia, aunque la velocidad aumenta). Si la aceleración no es perpendicular a la velocidad, entonces hay cierta aceleración en la dirección de desplazamiento, influyendo en la velocidad. Si la velocidad es constante, entonces la aceleración debe ser ortogonal a la velocidad, ya que entonces solo afecta a la dirección, y no a la velocidad.

idea clave: 52 Objetos con Velocidad Constante

Si un objeto se mueve con velocidad constante, entonces sus vectores de velocidad y aceleración son ortogonales. Es decir,\(\vecs v (t)cdot\vecs a (t)=0\).

Movimiento de proyectiles

Una aplicación importante de las funciones de posición valoradas por vectores es el movimiento de proyectiles: el movimiento de objetos bajo la influencia de la gravedad. Mediremos el tiempo en segundos, y las distancias serán en metros o pies. Mostraremos que podemos describir completamente la trayectoria de tal objeto conociendo su posición inicial y velocidad inicial (es decir, dónde está y hacia dónde va).

Supongamos que un objeto tiene posición inicial\(\vecs r(0) = \langle x_0,y_0\rangle\) y velocidad inicial\(\vecs v(0) = \langle v_x,v_y\rangle\). Se acostumbra reescribir\(\vecs v(0)\) en términos de su velocidad\(v_0\) y dirección\(\vecs u\), donde\(\vecs u\) es un vector unitario. Recordar todos los vectores unitarios en se\(\mathbb{R}^2\) pueden escribir como\(\langle \cos \theta,\sin \theta\rangle\), donde\(\theta\) es una medida de ángulo en sentido antihorario desde el\(x\) eje. (Nos referimos\(\theta\) como el ángulo de elevación.) Así\(\vecs v(0) = v_0\langle \cos \theta,\sin \theta\rangle.\)

Dado que se conoce la aceleración del objeto, es decir\(\vecs a (t) = \langle 0,-g\rangle\), dónde\(g\) está la constante gravitacional, podemos encontrar\(\vecs r (t)\) conociendo nuestras dos condiciones iniciales. Primero encontramos\ (\ vecs v (t)):

Nota

En este texto usamos\(g=32\) ft/s cuando se usan unidades imperiales, y\(g=9.8\) m/s cuando se usan unidades SI.

\ [\ begin {align*}
\ vecs v (t) &=\ int\ vecs a (t) dt\\ [4pt]
\ vecs v (t) &=\ int\ langle 0, -g\ rangle dt\\ [4pt]
\ vecs v (t) &=\ langle 0, -gt\ rangle +\ vecs C.
\ end {align*}\]

Sabiendo\(\vecs v(0) = v_0\langle \cos \theta,\sin \theta\rangle\), tenemos\(\vecs C = v_0\langle \cos t,\sin t\rangle\) y así

\[\vecs v(t) = \langle v_0\cos \theta, -gt+v_0\sin\theta\rangle.\]

Nos integramos una vez más para encontrar\(\vecs r (t)\):

\ [\ begin {align*}
\ vecs r (t) &=\ int\ vecs v (t) dt\\ [4pt]
\ vecs r (t) &=\ int\ langle v_0\ cos\ theta, -gt+v_0\ sin\ theta\ rangle dt\\ [4pt]
\ vecs r (t) &=\ langle\ big (v_0\ cos\ theta\ grande) t, -\ dfrac12gt^2+\ grande (v_0\ sin\ theta\ grande) t\ rangle +\ vecs C.\\ [4pt]
\ text {Sabiendo\(\vecs r(0) = \langle x_0,y_0\rangle\), concluimos\(\vecs C = \langle x_0,y_0\rangle\) y} &\\ [4pt]
\ vecs r (t) &=\ langle\ big (v_0\ cos\ theta\ big) t+x_0\, -\ dfrac12gt^2+\ big (v_0\ sin\ theta\ big) t+y_0\\ rangle.
\ end {alinear*}\]

idea clave 53: Movimiento de proyectiles

La función de posición de un proyectil propulsado desde una posición inicial de\(\vecs r_0=\langle x_0,y_0\rangle\), con velocidad inicial\(v_0\), con ángulo de elevación\(\theta\) y descuidando todas las aceleraciones menos la gravedad es

\[\vecs r (t) = \langle \big(v_0\cos \theta\big)t+x_0\ , -\dfrac12gt^2+\big(v_0\sin\theta\big)t+y_0\ \rangle.\]

Dejando\(\vecs v_0 = v_0\langle \cos \theta,\sin \theta\rangle\), (\ vecs r (t)\) se puede escribir como

\[\vecs r (t) = \langle 0,-\dfrac12gt^2\rangle + \vecs v_0t+\vecs r_0.\]

Demostramos cómo usar esta función de posición en los siguientes dos ejemplos.

Ejemplo\(\PageIndex{5}\): Projectile Motion

Sydney dispara su cañón BB Red Ryder a través del suelo nivelado desde una elevación de 4 pies, donde el cañón de la pistola hace un\(5^\circ\) ángulo con la horizontal. Encuentra hasta dónde viaja el bb antes de aterrizar, asumiendo que el bb se dispara a la tasa anunciada de 350ft/s e ignorando la resistencia del aire.

Solución

Una aplicación directa de Key Idea 53 da

\ [\ begin {alinear*}
\ vecs r (t) &=\ langle (350\ cos 5^\ circ) t, -16t^2 + (350\ sin 5^\ circ) t + 4\ rangle\\ [4pt]
&\ aprox.\ langle 346.67t, -16t^2+30.50t+4\ rangle,
\ end {align*}\]

donde fijamos su posición inicial para estar\(\langle 0,4\rangle\).
Tenemos que encontrar cuando el bb aterriza, entonces podemos encontrar donde. Logramos esto estableciendo el\(y\) -component igual a 0 y resolviendo para\(t\):

\ [\ begin {align*}
-16t^2+30.50t+4 &= 0\\ [4pt]
t &=\ dfrac {-30.50\ pm\ sqrt {30.50^2-4 (-16) (4)}} {-32}\\ [4pt]
t &\ approx 2.03s.
\ end {alinear*}\]

(Descartamos una solución negativa que resultó de nuestra ecuación cuadrática).

Hemos encontrado que el bb aterriza 2.03s después del disparo; con\(t=2.03\), encontramos que el\(x\) -componente de nuestra función de posición es\(346.67(2.03) = 703.74\) ft. El bb aterriza a unos 704 pies de distancia.

Ejemplo\(\PageIndex{6}\): Projectile Motion

Alex sostiene la pistola bb de su hermana a una altura de 3 pies y quiere disparar a un objetivo que se encuentra a 6 pies sobre el suelo, a 25 pies de distancia. ¿En qué ángulo debería sostener el arma para golpear su objetivo? (Seguimos suponemos que la velocidad del hocico es 350ft/s.)

Solución

La función de posición para el camino del bb de Alex es

\[\vecs r (t) = \langle (350\cos \theta)t, -16t^2+(350\sin\theta)t+3\rangle. \nonumber\]

Tenemos que encontrar para\(\theta\) que\(\vecs r (t)\) =\ langle 25,6\ rangle\) por algún valor de\(t\). Es decir, queremos encontrar\(\theta\) y\(t\) tal que

\[(350\cos\theta)t = 25 \quad \text{and}\quad -16t^2+(350\sin\theta)t+3 = 6. \nonumber\]

Esto no es trivial (aunque no “duro”). Comenzamos resolviendo cada ecuación para\(\cos\theta\) y\(\sin \theta\), respectivamente.

\[\cos\theta = \dfrac{25}{350t} \quad \text{and} \quad \sin\theta = \dfrac{3+16t^2}{350t}. \nonumber\]

Usando la Identidad Pitagórica\(\cos^2\theta+\sin^2\theta=1\), tenemos

\[\left(\dfrac{25}{350t}\right)^2 + \left(\dfrac{3+16t^2}{350t}\right)^2 =1 \nonumber\]

Multiplica ambos lados por\((350t)^2\):

\[\begin{align*}25^2 + (3+16t^2)^2 &=350^2t^2\\[4pt] 256t^4-122,404t^2+634 &=0.\end{align*}\]

Esta es una cuadrática en\(t^2\). Es decir, podemos aplicar la fórmula cuadrática para encontrar\(t^2\), luego resolver por\(t\) sí mismo.

\ [\ begin {align*}
t^2 &=\ dfrac {122,404\ pm\ sqrt {122,404^2-4 (256) (634)}} {512}\\ [4pt]
t^2 &= 0.0052,\ 478.135\\ [4pt]
t &=\ pm 0.072,\\ pm 21.866
\ end {align*}\]

Claramente los\(t\) valores negativos no se ajustan a nuestro contexto, así que tenemos\(t=0.072\) y\(t=21.866\). Usando\(\cos \theta = 25/(350 t)\), podemos resolver para\(\theta\):

\ [\ begin {align*}
\ theta &=\ cos^ {-1}\ izquierda (\ dfrac {25} {350\ cdot 0.072}\ derecha)\ quad\ text {y}\ quad\ cos^ {-1}\ izquierda (\ dfrac {25} {350\ cdot 21.866}\ derecha)\\ [4pt]
\ theta &= 7.03^\ c\ quad\ texto {y}\ quad 89.8^\ circ.
\ end {alinear*}\]

Alex tiene dos opciones de ángulo. Puede sostener el rifle en un ángulo de aproximadamente\(7^\circ\) con la horizontal y golpear su objetivo\(0.07\) s después de disparar, o puede sostener su rifle casi recto hacia arriba, con un ángulo de\(89.8^\circ\), donde golpeará su objetivo unos 22s después. La primera opción es claramente la opción que debe elegir.

Distancia recorrida

Considera a un conductor que pone su crucero-control a 60 mph, y viaja a esta velocidad durante una hora. Podemos preguntar:

1. ¿Hasta dónde viajó el chofer?
2. ¿A qué distancia de su posición inicial está la conductora?

El primero es fácil de responder: viajó 60 millas. El segundo es imposible de responder con la información dada. No sabemos si viajó en línea recta, en una pista de carreras ovalada, o por una carretera lentamente sinuosa.

Esto resalta un dato importante: para calcular la distancia recorrida, sólo necesitamos conocer la velocidad, dada por\(\norm{\vecs v (t)}\).

teorema 96: Distancia recorrida

Let\(\vecs v (t)\) Ser una función de velocidad para un objeto en movimiento. La distancia recorrida por el objeto\([a,b]\) es:

\[\text{distance traveled} = \int_a^b \norm{\vecs v (t)} dt .\]

Tenga en cuenta que esto es solo una reexpresión del Teorema 95: la longitud del arco es la misma que la distancia recorrida, solo vista en un contexto diferente.

Ejemplo\(\PageIndex{7}\): Distance Traveled, Displacement, and Average Speed

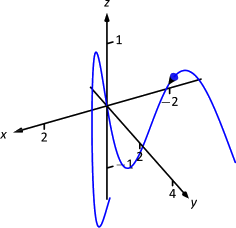
Una partícula se mueve en el espacio con la función de posición\(\vecs r (t) = \langle t,t^2,\sin (\pi t)\rangle\) activada\([-2,2]\), donde\(t\) se mide en segundos y las distancias son en metros. Encuentra:

1. La distancia recorrida por la partícula en\([-2,2]\).
2. El desplazamiento de la partícula en\([-2,2]\).
3. La velocidad promedio de la partícula.

Solución

1. Utilizamos el Teorema 96 para establecer la integral:\[\begin{align*}\text{distance traveled} &= \int_{-2}^2 \norm{\vecs v (t)} dt \\[4pt]&= \int_{-2}^2 \sqrt{1+(2t)^2+ \pi^2\cos^2(\pi t)} dt .\end{align*}\] Esto no se puede resolver en términos de funciones elementales por lo que volvemos a la integración numérica, encontrando que la distancia es de 12.88m.
2. El desplazamiento es el vector Es\[\vecs r(2)-\vecs r(-2) = \langle 2,4,0\rangle - \langle -2,4,0\rangle = \langle 4,0,0\rangle. \nonumber\] decir, la partícula termina con un\(x\) -valor incrementado en 4 y con\(y\) - y\(z\) -valores iguales (ver Figura\(\PageIndex{5}\)).
3. Encontramos arriba que la partícula viajó 12.88m a lo largo de 4 segundos. Podemos calcular la velocidad promedio dividiendo: 12.88/4 = 3.22m/s También
   
   debemos considerar la Definición 22 de la Sección 5.4, que dice que el valor promedio de una función\(f\) on\([a,b]\) es\(\dfrac{1}{b-a}\int_a^b f(x)\ dx\). En nuestro contexto, el valor promedio de la velocidad es\[\text{average speed} = \dfrac{1}{2-(-2)}\int_{-2}^2 \norm{\vecs v (t)} dt \approx \dfrac14 12.88 = 3.22\text{m/s}. \nonumber \]
   
   Obsérvese cómo el contexto físico de una partícula viajando da sentido a un concepto más abstracto aprendido anteriormente.

Figura\(\PageIndex{5}\): La trayectoria de la partícula en el Ejemplo 11.3.7

En la Definición 22 del Capítulo 5 definimos el valor promedio de una función\(f(x)\) en\([a,b]\) ser

\[ \dfrac{1}{b-a}\int_a^bf(x) dx.\]

Observe cómo en el Ejemplo 11.3.7 calculamos la velocidad promedio como

\[\dfrac{\text{distance traveled}}{\text{travel time}} = \dfrac1{2-(-2)}\int_{-2}^2\norm{\vecs v (t)} dt ;\]

es decir, acabamos de encontrar el valor promedio de\(\norm{\vecs v (t)}\) on\([-2,2]\).

Del mismo modo, dada la función de posición\(\vecs r (t)\), la velocidad promedio\([a,b]\) es

\[\dfrac{\text{displacement}}{\text{travel time}} = \dfrac1{b-a}\int_a^b \vecs{r}\,'(t) dt = \dfrac{\vecs r(b)-\vecs r(a)}{b-a};\]

es decir, es el valor promedio de\(\vecs r\,'(t)\), o\(\vecs v (t)\), on\([a,b]\).

KEY IDEA 54: Velocidad Media, Velocidad Media

Dejar\(\vecs r(t)\) ser una función de posición continua en un intervalo abierto\(I\) que contiene\(a<b\).

• La velocidad promedio es:

\[\dfrac{\text{distance traveled}}{\text{travel time}} = \dfrac{\int_a^b \norm{\vecs v (t)} dt }{b-a} = \dfrac1{b-a}\int_a^b\norm{\vecs v (t)} dt .\]

• La velocidad promedio es:

\[\dfrac{\text{displacement}}{\text{travel time}} = \dfrac{\int_a^b \vecs{r}\,'(t) dt }{b-a} = \dfrac1{b-a}\int_a^b\vecs{r}\,'(t) dt .\]

Las siguientes dos secciones investigan más propiedades de las gráficas de funciones vectoriales y aplicaremos estas nuevas ideas a lo que acabamos de aprender sobre el movimiento.