1.1E: Ejercicios para la Sección 1.1
- Page ID
- 116844
Para los ejercicios 1 a 6, (a) determinar el dominio y el rango de cada relación, y (b) indicar si la relación es una función.
1)
| \(x\) | \(y\) | \(x\) | \(y\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">-3 | \ (y\)” style="text-align:center; ">9 | \ (x\)” style="text-align:center; ">1 | \ (y\)” style="text-align:center; ">1 |
| \ (x\)” style="text-align:center; ">-2 | \ (y\)” style="text-align:center; ">4 | \ (x\)” style="text-align:center; ">2 | \ (y\)” style="text-align:center; ">4 |
| \ (x\)” style="text-align:center; ">-1 | \ (y\)” style="text-align:center; ">1 | \ (x\)” style="text-align:center; ">3 | \ (y\)” style="text-align:center; ">9 |
| \ (x\)” style="text-align:center; ">0 | \ (y\)” style="text-align:center; ">0 | \ (x\)” style="text-align:center; "> | \ (y\)” style="text-align:center; "> |
- Contestar
-
a. Dominio = {\(−3,−2,−1,0,1,2,3\)}, Rango = {\(0,1,4,9\)}
b. Sí, una función
2)
| \(x\) | \(y\) | \(x\) | \(y\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">-3 | \ (y\)” style="text-align:center; ">-2 | \ (x\)” style="text-align:center; ">1 | \ (y\)” style="text-align:center; ">1 |
| \ (x\)” style="text-align:center; ">-2 | \ (y\)” style="text-align:center; ">-8 | \ (x\)” style="text-align:center; ">2 | \ (y\)” style="text-align:center; ">8 |
| \ (x\)” style="text-align:center; ">-1 | \ (y\)” style="text-align:center; ">-1 | \ (x\)” style="text-align:center; ">3 | \ (y\)” style="text-align:center; ">-2 |
| \ (x\)” style="text-align:center; ">0 | \ (y\)” style="text-align:center; ">0 | \ (x\)” style="text-align:center; "> | \ (y\)” style="text-align:center; "> |
3)
| \(x\) | \(y\) | \(x\) | \(y\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">1 | \ (y\)” style="text-align:center; ">-3 | \ (x\)” style="text-align:center; ">1 | \ (y\)” style="text-align:center; ">1 |
| \ (x\)” style="text-align:center; ">2 | \ (y\)” style="text-align:center; ">-2 | \ (x\)” style="text-align:center; ">2 | \ (y\)” style="text-align:center; ">2 |
| \ (x\)” style="text-align:center; ">3 | \ (y\)” style="text-align:center; ">-1 | \ (x\)” style="text-align:center; ">3 | \ (y\)” style="text-align:center; ">3 |
| \ (x\)” style="text-align:center; ">0 | \ (y\)” style="text-align:center; ">0 | \ (x\)” style="text-align:center; "> | \ (y\)” style="text-align:center; "> |
- Contestar
-
a. Dominio = {\(0,1,2,3\)}, Rango = {\(−3,−2,−1,0,1,2,3\)}
b. No, no es una función
4)
| \(x\) | \(y\) | \(x\) | \(y\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">1 | \ (y\)” style="text-align:center; ">1 | \ (x\)” style="text-align:center; ">5 | \ (y\)” style="text-align:center; ">1 |
| \ (x\)” style="text-align:center; ">2 | \ (y\)” style="text-align:center; ">1 | \ (x\)” style="text-align:center; ">6 | \ (y\)” style="text-align:center; ">1 |
| \ (x\)” style="text-align:center; ">3 | \ (y\)” style="text-align:center; ">1 | \ (x\)” style="text-align:center; ">7 | \ (y\)” style="text-align:center; ">1 |
| \ (x\)” style="text-align:center; ">4 | \ (y\)” style="text-align:center; ">1 | \ (x\)” style="text-align:center; "> | \ (y\)” style="text-align:center; "> |
5)
| \(x\) | \(y\) | \(x\) | \(y\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">3 | \ (y\)” style="text-align:center; ">3 | \ (x\)” style="text-align:center; ">15 | \ (y\)” style="text-align:center; ">1 |
| \ (x\)” style="text-align:center; ">5 | \ (y\)” style="text-align:center; ">2 | \ (x\)” style="text-align:center; ">21 | \ (y\)” style="text-align:center; ">2 |
| \ (x\)” style="text-align:center; ">8 | \ (y\)” style="text-align:center; ">1 | \ (x\)” style="text-align:center; ">33 | \ (y\)” style="text-align:center; ">3 |
| \ (x\)” style="text-align:center; ">10 | \ (y\)” style="text-align:center; ">0 | \ (x\)” style="text-align:center; "> | \ (y\)” style="text-align:center; "> |
- Contestar
-
a. Dominio = {\(3,5,8,10,15,21,33\)}, Rango = {\(0,1,2,3\)}
b. Sí, una función
6)
| \(x\) | \(y\) | \(x\) | \(y\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">-7 | \ (y\)” style="text-align:center; ">11 | \ (x\)” style="text-align:center; ">1 | \ (y\)” style="text-align:center; ">-2 |
| \ (x\)” style="text-align:center; ">-2 | \ (y\)” style="text-align:center; ">5 | \ (x\)” style="text-align:center; ">3 | \ (y\)” style="text-align:center; ">4 |
| \ (x\)” style="text-align:center; ">-2 | \ (y\)” style="text-align:center; ">1 | \ (x\)” style="text-align:center; ">6 | \ (y\)” style="text-align:center; ">11 |
| \ (x\)” style="text-align:center; ">0 | \ (y\)” style="text-align:center; ">-1 | \ (x\)” style="text-align:center; "> | \ (y\)” style="text-align:center; "> |
Para los ejercicios 7 - 13, encuentre los valores para cada función, si existen, luego simplifique.
a.\(f(0)\) b.\(f(1)\) c.\(f(3)\) d.\(f(−x)\) e.\(f(a)\) f.\(f(a+h)\)
7)\(f(x)=5x−2\)
- Contestar
- a.\(−2\) b.\(3\) c.\(13\) d.\(−5x−2\) e.\(5a−2\) f.\(5a+5h−2\)
8)\(f(x)=4x^2−3x+1\)
9)\(f(x)=\dfrac{2}{x}\)
- Contestar
- a. Indefinido b.\(2\) c.\(\frac{2}{3}\) d.\(−\dfrac{2}{x}\) e.\(\dfrac{2}{a}\) f.\(\dfrac{2}{a+h}\)
10)\(f(x)=|x−7|+8\)
11)\(f(x)=\sqrt{6x+5}\)
- Contestar
- a.\(\sqrt{5}\) b.\(\sqrt{11}\) c.\(\sqrt{23}\) d.\(\sqrt{−6x+5}\) e.\(\sqrt{6a+5}\) f.\(\sqrt{6a+6h+5}\)
12)\(f(x)=\dfrac{x−2}{3x+7}\)
13)\(f(x)=9\)
- Contestar
- a. 9 b. 9 c. 9 d. 9 e. 9 f. 9
Para los ejercicios 14 - 21, encuentra el dominio, el rango y todos los zeros/intercepciones, en su caso, de las funciones.
14)\(f(x)=\dfrac{x}{x^2−16}\)
15)\(g(x)=\sqrt{8x−1}\)
- Contestar
- \(x≥\frac{1}{8};\quad y≥0;\quad x=\frac{1}{8}\); sin intercepción en Y
16)\(h(x)=\dfrac{3}{x^2+4}\)
17)\(f(x)=−1+\sqrt{x+2}\)
- Contestar
- \(x≥−2;\quad y≥−1;\quad x=−1;\quad y=−1+\sqrt{2}\)
18)\(f(x)=1x−\sqrt{9}\)
19)\(g(x)=\dfrac{3}{x−4}\)
- Contestar
- \(x≠4;\quad y≠0\); sin intercepción x;\(y=−\frac{3}{4}\)
20)\(f(x)=4|x+5|\)
21)\(g(x)=\sqrt{\dfrac{7}{x−5}}\)
- Contestar
- \(x>5;\quad y>0\); sin intercepciones
Para los ejercicios 22 - 27, configura una tabla para bosquejar la gráfica de cada función utilizando los siguientes valores:\(x=−3,−2,−1,0,1,2,3.\)
22)\(f(x)=x^2+1\)
| \(x\) | \(y\) | \(x\) | \(y\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">-3 | \ (y\)” style="text-align:center; ">10 | \ (x\)” style="text-align:center; ">1 | \ (y\)” style="text-align:center; ">2 |
| \ (x\)” style="text-align:center; ">-2 | \ (y\)” style="text-align:center; ">5 | \ (x\)” style="text-align:center; ">2 | \ (y\)” style="text-align:center; ">5 |
| \ (x\)” style="text-align:center; ">-1 | \ (y\)” style="text-align:center; ">2 | \ (x\)” style="text-align:center; ">3 | \ (y\)” style="text-align:center; ">10 |
| \ (x\)” style="text-align:center; ">0 | \ (y\)” style="text-align:center; ">1 | \ (x\)” style="text-align:center; "> | \ (y\)” style="text-align:center; "> |
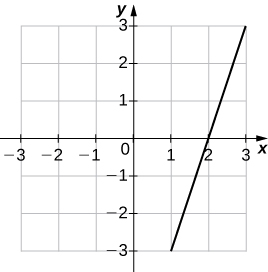
23)\(f(x)=3x−6\)
| \(x\) | \(y\) | \(x\) | \(y\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">-3 | \ (y\)” style="text-align:center; ">-15 | \ (x\)” style="text-align:center; ">1 | \ (y\)” style="text-align:center; ">-3 |
| \ (x\)” style="text-align:center; ">-2 | \ (y\)” style="text-align:center; ">-12 | \ (x\)” style="text-align:center; ">2 | \ (y\)” style="text-align:center; ">0 |
| \ (x\)” style="text-align:center; ">-1 | \ (y\)” style="text-align:center; ">-9 | \ (x\)” style="text-align:center; ">3 | \ (y\)” style="text-align:center; ">3 |
| \ (x\)” style="text-align:center; ">0 | \ (y\)” style="text-align:center; ">-6 | \ (x\)” style="text-align:center; "> | \ (y\)” style="text-align:center; "> |
- Contestar
24)\(f(x)=\frac{1}{2}x+1\)
| \(x\) | \(y\) | \(x\) | \(y\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">-3 | \ (y\)” style="text-align:center; ">\(-\frac{1}{2}\) | \ (x\)” style="text-align:center; ">1 | \ (y\)” style="text-align:center; ">\(\frac{3}{2}\) |
| \ (x\)” style="text-align:center; ">-2 | \ (y\)” style="text-align:center; ">0 | \ (x\)” style="text-align:center; ">2 | \ (y\)” style="text-align:center; ">2 |
| \ (x\)” style="text-align:center; ">-1 | \ (y\)” style="text-align:center; ">\(\frac{1}{2}\) | \ (x\)” style="text-align:center; ">3 | \ (y\)” style="text-align:center; ">\(\frac{5}{2}\) |
| \ (x\)” style="text-align:center; ">0 | \ (y\)” style="text-align:center; ">1 | \ (x\)” style="text-align:center; "> | \ (y\)” style="text-align:center; "> |
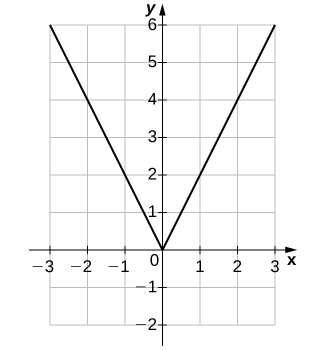
25)\(f(x)=2|x|\)
| \(x\) | \(y\) | \(x\) | \(y\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">-3 | \ (y\)” style="text-align:center; ">6 | \ (x\)” style="text-align:center; ">1 | \ (y\)” style="text-align:center; ">2 |
| \ (x\)” style="text-align:center; ">-2 | \ (y\)” style="text-align:center; ">4 | \ (x\)” style="text-align:center; ">2 | \ (y\)” style="text-align:center; ">4 |
| \ (x\)” style="text-align:center; ">-1 | \ (y\)” style="text-align:center; ">2 | \ (x\)” style="text-align:center; ">3 | \ (y\)” style="text-align:center; ">6 |
| \ (x\)” style="text-align:center; ">0 | \ (y\)” style="text-align:center; ">0 | \ (x\)” style="text-align:center; "> | \ (y\)” style="text-align:center; "> |
- Contestar
26)\(f(x)=-x^2\)
| \(x\) | \(y\) | \(x\) | \(y\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">-3 | \ (y\)” style="text-align:center; ">-9 | \ (x\)” style="text-align:center; ">1 | \ (y\)” style="text-align:center; ">-1 |
| \ (x\)” style="text-align:center; ">-2 | \ (y\)” style="text-align:center; ">-4 | \ (x\)” style="text-align:center; ">2 | \ (y\)” style="text-align:center; ">-4 |
| \ (x\)” style="text-align:center; ">-1 | \ (y\)” style="text-align:center; ">-1 | \ (x\)” style="text-align:center; ">3 | \ (y\)” style="text-align:center; ">-9 |
| \ (x\)” style="text-align:center; ">0 | \ (y\)” style="text-align:center; ">0 | \ (x\)” style="text-align:center; "> | \ (y\)” style="text-align:center; "> |
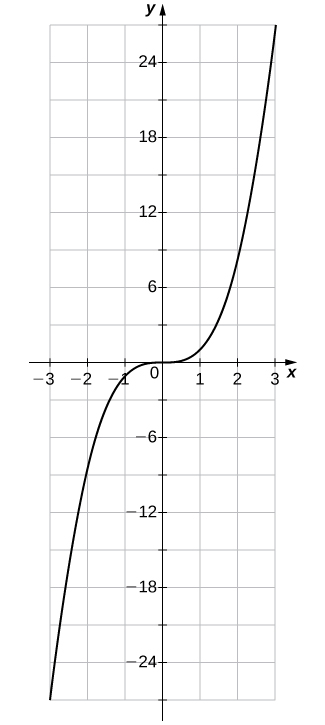
27)\(f(x)=x^3\)
| \(x\) | \(y\) | \(x\) | \(y\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">-3 | \ (y\)” style="text-align:center; ">-27 | \ (x\)” style="text-align:center; ">1 | \ (y\)” style="text-align:center; ">1 |
| \ (x\)” style="text-align:center; ">-2 | \ (y\)” style="text-align:center; ">-8 | \ (x\)” style="text-align:center; ">2 | \ (y\)” style="text-align:center; ">8 |
| \ (x\)” style="text-align:center; ">-1 | \ (y\)” style="text-align:center; ">-1 | \ (x\)” style="text-align:center; ">3 | \ (y\)” style="text-align:center; ">27 |
| \ (x\)” style="text-align:center; ">0 | \ (y\)” style="text-align:center; ">0 | \ (x\)” style="text-align:center; "> | \ (y\)” style="text-align:center; "> |
- Contestar
Para los ejercicios 28 - 35, utilice la prueba de línea vertical para determinar si cada una de las gráficas dadas representa una función. Supongamos que una gráfica continúa en ambos extremos si se extiende más allá de la cuadrícula dada. Si la gráfica representa una función, entonces determine lo siguiente para cada gráfica:
a. Dominio y rango
b.\(x\) -interceptar, en su caso (estimación cuando sea necesario)
c.\(y\) -Interceptar, en su caso (estimación cuando sea necesario)
d. Los intervalos para los que la función está aumentando
e. Los intervalos para los que la función está disminuyendo
f. Los intervalos para los que la función es constante
g. Simetría alrededor de cualquier eje y/o el origen
h. Si la función es par, impar o ninguna
28)
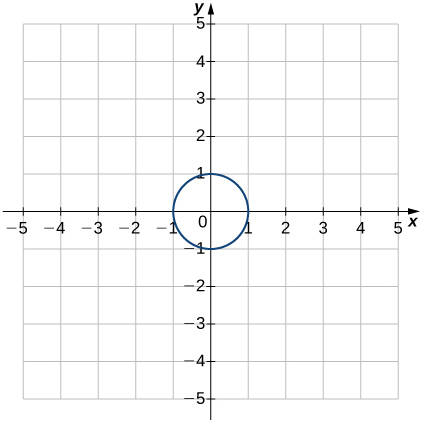
29)
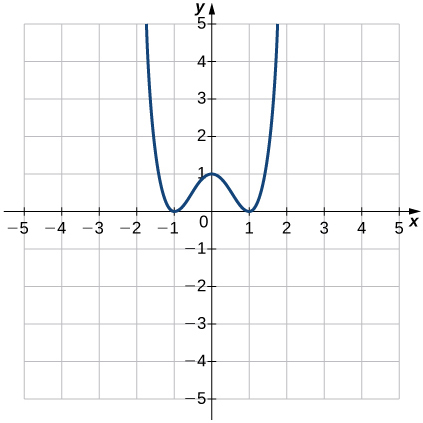
- Contestar
- Función;
a. Dominio: todos los números reales, rango:\(y≥0\)
b.\(x=±1\)
c.\(y=1\)
d.\(−1<x<0\) y\(1<x<∞\)
e.\(−∞<x<−1\) y\(0<x<1\)
f. No constante
g. \(y\)-eje
h. Incluso
30)
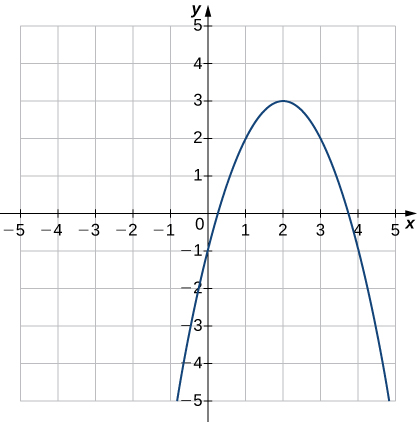
31)
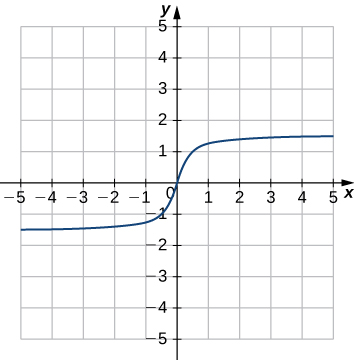
- Contestar
- Función;
a. Dominio: todos los números reales, rango:\(−1.5≤y≤1.5\)
b.\(x=0\)
c.\(y=0\)
d. todos los números reales
e. Ninguno
f. No constante
g. Origen
h. Impar
32)
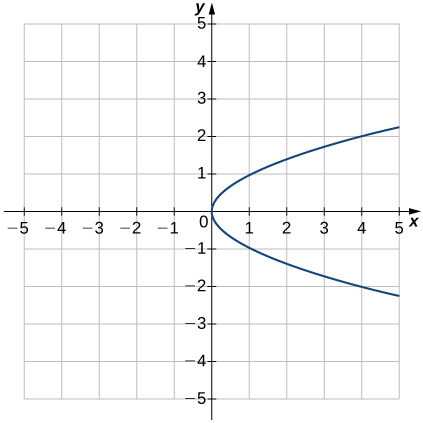
33)
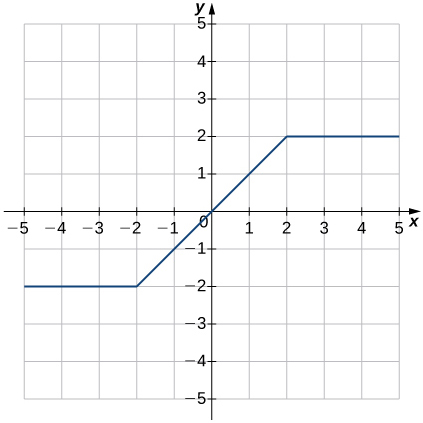
- Contestar
- Función;
a. Dominio:\(−∞<x<∞\), rango:\(−2≤y≤2\)
b.\(x=0\)
c.\(y=0\)
d.\(−2<x<2\)
e. No decreciente
f.\(−∞<x<−2\) y\(2<x<∞\)
g. Origen
h. impar
34)
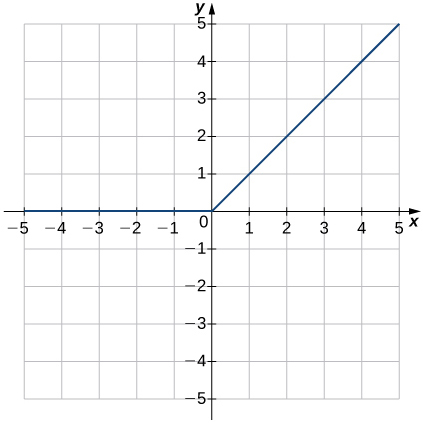
35)
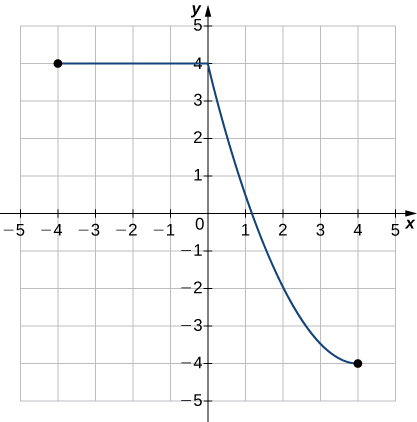
- Contestar
- Función;
a. Dominio:\(−4≤x≤4\), rango:\(−4≤y≤4\)
b.\(x=1.2\)
c.\(y=4\)
d. No creciente
e.\(0<x<4\)
f.\(−4<x<0\)
g. Sin simetría
h. Ni
Para los ejercicios 36 - 41, por cada par de funciones, encontrar a.\(f+g\) b.\(f−g\) c.\(f⋅g\) d\(f/g\). Determinar el dominio de cada una de estas nuevas funciones.
36)\(f(x)=3x+4,\quad g(x)=x−2\)
37)\(f(x)=x−8,\quad g(x)=5x^2\)
- Contestar
- a.\(5x^2+x−8\); todos los números reales
b.\(−5x^2+x−8\); todos los números reales
c.\(5x^3−40x^2\); todos los números reales
d.\(\dfrac{x−8}{5x^2};\quad x≠0\)
38)\(f(x)=3x^2+4x+1,\quad g(x)=x+1\)
39)\(f(x)=9−x^2,\quad g(x)=x^2−2x−3\)
- Contestar
- a.\(−2x+6\); todos los números reales
b.\(−2x^2+2x+12\); todos los números reales
c.\(−x^4+2x^3+12x^2−18x−27\); todos los números reales
d.\(−\dfrac{x+3}{x+1};\quad x≠−1,3\)
40)\(f(x)=\sqrt{x},\quad g(x)=x−2\)
41)\(f(x)=6+\dfrac{1}{x},\quad g(x)=\dfrac{1}{x}\)
- Contestar
-
a.\(6+\dfrac{2}{x};\quad x≠0\)
b.\(6; \quad x≠0\)
c.\(6x+\dfrac{1}{x^2};\quad x≠0\)
d.\(6x+1;\quad x≠0\)
Para los ejercicios 42 - 48, para cada par de funciones, encuentre a.\((f∘g)(x)\) y b.\((g∘f)(x)\) Simplifique los resultados. Encuentra el dominio de cada uno de los resultados.
42)\(f(x)=3x,\quad g(x)=x+5\)
43)\(f(x)=x+4,\quad g(x)=4x−1\)
- Contestar
- a.\(4x+3\); todos los números reales
b.\(4x+15\); todos los números reales
44)\(f(x)=2x+4,\quad g(x)=x^2−2\)
45)\(f(x)=x^2+7,\quad g(x)=x^2−3\)
- Contestar
- a.\(x^4−6x^2+16\); todos los números reales
b.\(x^4+14x^2+46\); todos los números reales
46)\(f(x)=\sqrt{x}, \quad g(x)=x+9\)
47)\(f(x)=\dfrac{3}{2x+1},\quad g(x)=\dfrac{2}{x}\)
- Contestar
-
a.\(\dfrac{3x}{4+x};\quad x≠0,−4\)
b.\(\dfrac{4x+2}{3};\quad x≠−\frac{1}{2}\)
48)\(f(x)=|x+1|,\quad g(x)=x^2+x−4\)
49) La siguiente tabla enumera los ganadores del campeonato de la NBA para los años 2001 a 2012.
| Año | Ganador |
|---|---|
| 2001 | Los Lakers |
| 2002 | Los Lakers |
| 2003 | Sam Antonio Espuelas |
| 2004 | Detroit Pistones |
| 2005 | Sam Antonio Espuelas |
| 2006 | Miami Heat |
| 2007 | Sam Antonio Espuelas |
| 2008 | Boston Celtics |
| 2009 | Los Lakers |
| 2010 | Los Lakers |
| 2011 | Dallas Mavericks |
| 2012 | Miami Heat |
a. considerar la relación en la que los valores de dominio son los años 2001 a 2012 y el rango es el ganador correspondiente. ¿Esta relación es una función? Explique por qué o por qué no.
b. considerar la relación donde los valores de dominio son los ganadores y el rango son los años correspondientes. ¿Esta relación es una función? Explique por qué o por qué no.
- Contestar
- a. si, porque solo hay un ganador por cada año.
b. no, porque hay tres equipos que ganaron más de una vez durante los años 2001 a 2012.
50) [T] El área\(A\) de un cuadrado depende de la longitud del lado s.
a. Escribir una función\(A(s)\) para el área de un cuadrado.
b. Encontrar e interpretar\(A(6.5)\).
c. Encuentra la aproximación exacta y la de dos dígitos significativos a la longitud de los lados de un cuadrado con área 56 unidades cuadradas.
51) [T] El volumen de un cubo depende de la longitud de los lados\(s.\)
a. Escribir una función\(V(s)\) para el área de un cuadrado.
b. Encontrar e interpretar\(V(11.8)\).
- Contestar
- a.\(V(s)=s^3\)
b.\(V(11.8)≈1643\); un cubo de longitud lateral 11.8 cada uno tiene un volumen aproximado de 1643 unidades cúbicas.
52) [T] Una empresa de alquiler de autos alquila autos por una tarifa fija de $20 y un cargo por hora de $10.25. Por lo tanto, el costo total\(C\) para alquilar un auto es función de las horas en que se alquila\(t\) el auto más la tarifa plana.
a. escribir la fórmula para la función que modela esta situación.
b. encontrar el costo total para rentar un auto por 2 días y 7 horas.
c. Determinar por cuánto tiempo estuvo rentado el auto si la factura es de 432.73 dólares.
53) [T] Un vehículo tiene un tanque de 20 gal y obtiene 15 mpg. El número de millas\(N\) que se pueden conducir depende de la cantidad de gas\(x\) en el tanque.
a. Escribir una fórmula que modele esta situación.
b. Determinar el número de millas que el vehículo puede recorrer en (i) un tanque lleno de gasolina y (ii) 3/4 de un tanque de gasolina.
c. Determinar el dominio y el rango de la función.
d. Determinar cuántas veces la conductora tuvo que detenerse por gasolina si ha conducido un total de 578 millas.
- Contestar
- a.\(N(x)=15x\)
b. i.\(N(20)=15(20)=300\); por lo tanto, el vehículo puede recorrer 300 millas en un tanque lleno de gasolina.
ii. \(N(15)=225\); por lo tanto, el vehículo puede recorrer 225 millas en 3/4 de un tanque de gasolina.
c. Dominio:\(0≤x≤20\); rango:\([0,300]\)
d. El conductor tuvo que detenerse al menos una vez, dado que se necesitan aproximadamente 39 gal de gas para conducir un total de 578 millas.
54) [T] El volumen\(V\) de una esfera depende de la longitud de su radio como\(V=(4/3)πr^3\). Debido a que la Tierra no es una esfera perfecta, podemos usar el radio medio al medir desde el centro hasta su superficie. El radio medio es la distancia promedio desde el centro físico a la superficie, en base a un gran número de muestras. Encuentra el volumen de la Tierra con radio medio\(6.371×106\) m.
55) [T] Cierta bacteria crece en cultivo en una región circular. El radio del círculo, medido en centímetros, viene dado por\(r(t)=6−\dfrac{5}{t^2+1}\), donde\(t\) se mide el tiempo en horas desde que se colocó en el cultivo un círculo de un radio de 1 cm de la bacteria.
a. Expresar el área de la bacteria en función del tiempo.
b. Encontrar el área exacta y aproximada del cultivo bacteriano en 3 horas.
c. Expresar la circunferencia de la bacteria en función del tiempo.
d. Encuentra la circunferencia exacta y aproximada de la bacteria en 3 horas.
- Contestar
- a.\(A(t)=A(r(t))=π⋅(6−\frac{5}{t^2+1})^2\)
b. Exacta:\(\frac{121π}{4}\); aproximadamente\(95\text{ cm}^2\)
c.\(C(t)=C(r(t))=2π(6−\frac{5}{t^2+1})\)
d. Exacta:\(11π\); aproximadamente\(35\) cm
56) [T] Un turista estadounidense visita París y debe convertir dólares estadounidenses en euros, lo que se puede hacer utilizando la función\(E(x)=0.79x\), donde\(x\) está el número de dólares estadounidenses y\(E(x)\) es el número equivalente de euros. Dado que las tasas de conversión fluctúan, cuando el turista regresa a Estados Unidos 2 semanas después, la conversión de euros a dólares estadounidenses\(x\) es\(D(x)=1.245x\), donde está el número de euros y\(D(x)\) es el número equivalente de dólares estadounidenses.
a. Encuentre la función compuesta que convierte directamente de dólares estadounidenses a dólares estadounidenses a través de euros. ¿Perdió valor este turista en el proceso de conversión?
b. Use (a) para determinar cuántos dólares estadounidenses recuperaría el turista al final de su viaje si convertiera $200 extra cuando llegó a París.
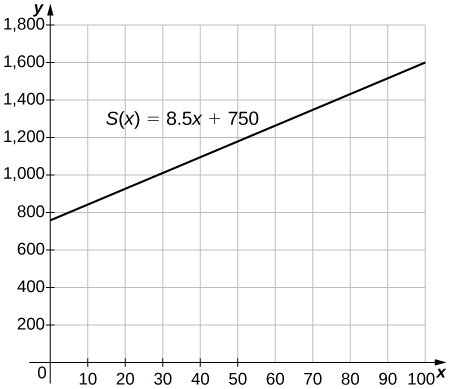
57) [T] El gerente de una tienda de patinetas paga a sus trabajadores un salario mensual\(S\) de $750 más una comisión de $8.50 por cada patineta que venden.
a.- Escribir una función\(y=S(x)\) que modele el salario mensual de un trabajador en función del número de patinetas\(x\) que vende.
b. encontrar el salario mensual aproximado cuando un trabajador vende 25, 40 o 55 patinetas.
c. Utilice la función INTERSECT en una calculadora gráfica para determinar el número de patinetas que deben venderse para que un trabajador obtenga un ingreso mensual de $1400. (Sugerencia: Encuentra la intersección de la función y la línea\(y=1400\).)
- Contestar
- a.\(S(x)=8.5x+750\) b. $962.50, $1090, $1217.50 c. 77 monopatines
58) [T] Utilice una calculadora gráfica para graficar el semicírculo\(y=\sqrt{25−(x−4)^2}\). Luego, use la función INTERCEPT para encontrar el valor de las intercepciones\(x\) - y\(y\) -intercepciones.