1.2E: Ejercicios para la Sección 1.2

Última actualización
Guardar como PDF

Page ID: 116787

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En los ejercicios 1 a 8, por cada par de puntos,

a. encontrar la pendiente de la línea que pasa por los puntos y

b. indicar si la línea es creciente, decreciente, horizontal o vertical.

1)$(-2,4)$ y$(1,1)$

Responder: a.$m = −1$
b. Disminución

2)$(-1,4)$ y$(3,-1)$

3)$(3,5)$ y$(-1,2)$

Responder: a.$m = 3/4$
b. Incrementando

4)$(6,4)$ y$(4,-3)$

5)$(2,3)$ y$(5,7)$

Contestar: a.$m = 4/3$
b. Incrementando

6)$(1,9)$ y$(-8,5)$

7)$(2,4)$ y$(1,4)$

Contestar: a.$m = 0$
b. Horizontal

8)$(1,4)$ y$(1,0)$

En los ejercicios 9 - 16, escriba la ecuación de la línea satisfaciendo las condiciones dadas en forma de pendiente-intercepción.

9) Pendiente =$−6$, pasa$(1,3)$

Contestar: $y=−6x+9$

10) Pendiente =$3$, pasa$(-3,2)$

11) Pendiente =$\frac{1}{3}$, pasa$(0,4)$

Contestar: $y=\frac{1}{3}x+4$

12) Pendiente =$\frac{2}{5}$,$x$ -intercepción =$8$

13) Pasando a través$(2,1)$ y$(−2,−1)$

Contestar: $y=\frac{1}{2}x$

14) Pasando a través$(−3,7)$ y$(1,2)$

15)$x$ -intercept =$5$ y$y$ -intercept =$−3$

Contestar: $y=\frac{3}{5}x−3$

16)$x$ -Intercept =−$6$ y$y$ -intercept =$9$

En los ejercicios 17 a 24, para cada ecuación lineal,

a. dar la pendiente$m$ y$y$ -interceptar$b,$ si lo hay, y

b. graficar la línea.

17)$y=2x−3$

Contestar

a.$m=2,\;b=−3$

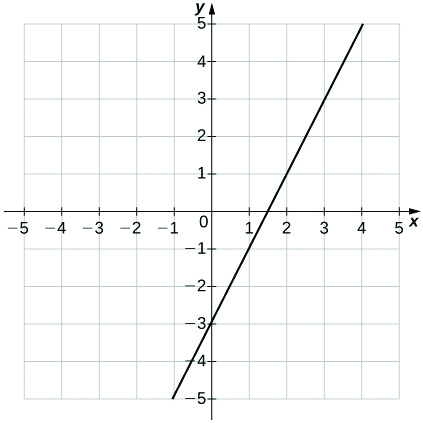
$Una imagen de una gráfica. El eje x va de -5 a 5 y el eje y va de -5 a 5. La gráfica muestra una función de línea recta creciente con una intercepción y en (0, -3) y una intercepción x en (1.5, 0).$

18)$y=−\frac{1}{7}x+1$

19)$f(x)=-6x$

Contestar

a.$m=−6,\; b=0$

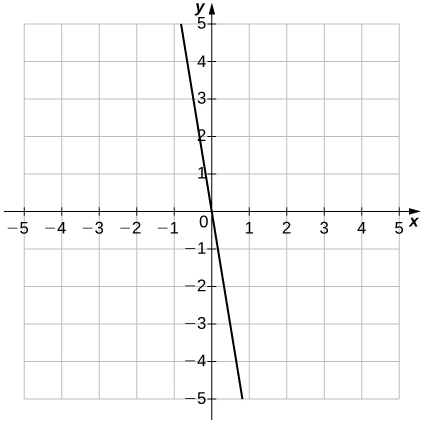
$Una imagen de una gráfica. El eje x va de -5 a 5 y el eje y va de -5 a 5. La gráfica muestra una función de línea recta decreciente con una intercepción y y una intercepción x ambas en el origen. Hay un punto sin etiquetar en la función en (0.5, -3).$

20)$f(x)=−5x+4$

21)$4y+24=0$

Contestar

a.$ m=0,\;b=−6$

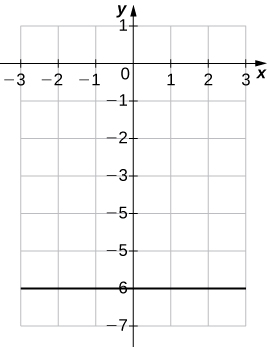
$Una imagen de una gráfica. El eje x va de -3 a 3 y el eje y va de -7 a 1. La gráfica muestra una función de línea recta horizontal con una intercepción y en (0, -6) y sin intercepción x.$

22)$8x-4=0$

23)$2x+3y=6$

Contestar

a.$m=−\frac{2}{3},\; b=2$

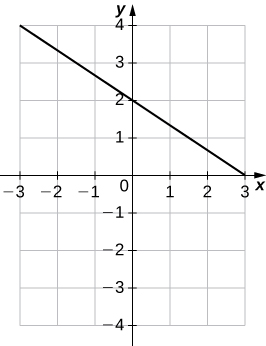
$Una imagen de una gráfica. El eje x va de -3 a 3 y el eje y va de -4 a 4. El gráfico muestra una función de línea recta decreciente con una intercepción y en (0, 2) y una intercepción x en (3, 0).$

24)$6x−5y+15=0$

En los ejercicios 25 a 29, por cada polinomio,

a. encontrar el grado;

b. encontrar los ceros, si los hubiere;

c. encontrar la (s)$y$ intercepción (es), si la hubiere;

d. utilizar el coeficiente inicial para determinar el comportamiento final de la gráfica; y

e. determinar algebraicamente si el polinomio es par, impar o ninguno.

25)$f(x)=2x^2−3x−5$

Contestar: a.$2$
b.$\frac{5}{2},\;−1$;
c.$−5$
d. Ambos extremos se elevan
e. Ninguno

26)$f(x)=−3x^2+6x$

27)$f(x)=\frac{1}{2}x^2−1$

Contestar: a.$2$
b. ±$\sqrt{2}$
c.$−1$
d. Ambos extremos se elevan
e. Incluso

28)$f(x)=x^3+3x^2−x−3$

29)$f(x)=3x−x^3$

Contestar: a.$3$
b.$0,$ ±$\sqrt{3}$
c.$0$
d. Extremo izquierdo sube, extremo derecho cae
e. Impares

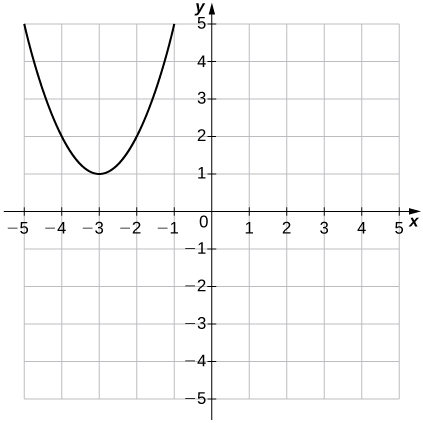
Para los ejercicios 30 - 31, utilice la gráfica de$f(x)=x^2$ para graficar cada función transformada$g$.

30)$g(x)=x^2−1$

31)$g(x)=(x+3)^2+1$

Contestar: $Una imagen de una gráfica. El eje x va de -5 a 5 y el eje y va de -5 a 5. El gráfico muestra una función parabólica que disminuye hasta el punto (-3, 1), luego comienza a aumentar. No se muestra la intercepción y y no hay intercepciones x. Hay dos puntos no trazados en (-4, 2) y (-2, 2).$

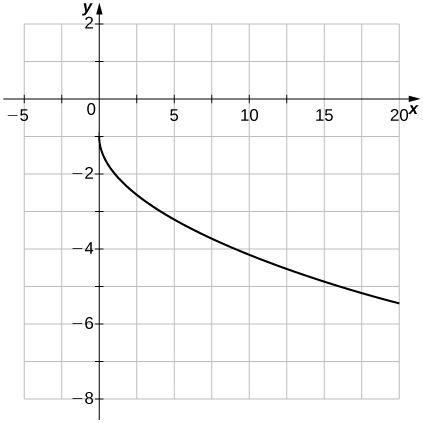
Para los ejercicios 32 - 33, utilice la gráfica de$f(x)=\sqrt{x}$ para graficar cada función transformada$g$.

32)$g(x)=\sqrt{x+2}$

33)$g(x)=−\sqrt{x}−1$

Contestar: $Una imagen de una gráfica. El eje x va de -5 a 20 y el eje y va de -8 a 2. El gráfico muestra una función curva que comienza en el punto (0, -1), luego comienza a disminuir. La intercepción y está en (0, -1) y no hay intercepción x. Hay un punto no trazado en (9, -4).$

Para los ejercicios 34 - 35, utilice la gráfica de$y=f(x)$ para graficar cada función transformada$g$.

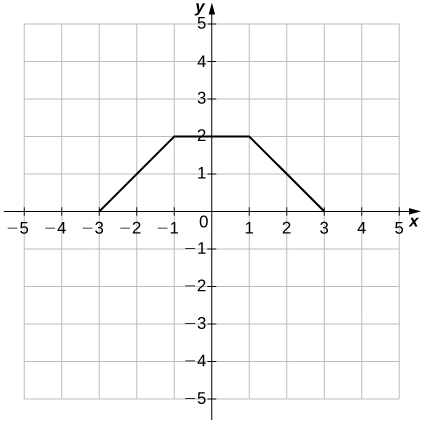
$Una imagen de una gráfica. El eje x va de -5 a 5 y el eje y va de -5 a 5. El gráfico muestra una función que inicia en el punto (-3, 0), donde comienza a aumentar hasta el punto (-1, 2). Después del punto (-1, 2), la función se convierte en una línea horizontal y permanece así hasta el punto (1, 2). Después del punto (1, 2), la función comienza a disminuir hasta el punto (3, 0), donde termina la función.$

34)$g(x)=f(x)+1$

35)$g(x)=f(x−1)+2$

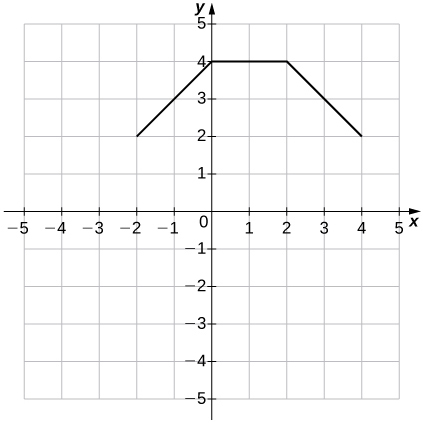
Contestar: $Una imagen de una gráfica. El eje x va de -5 a 5 y el eje y va de -5 a 5. El gráfico muestra una función que inicia en el punto (-2, 2), donde comienza a aumentar hasta el punto (0, 4). Después del punto (0, 4), la función se convierte en una línea horizontal y permanece así hasta el punto (2, 4). Después del punto (2, 4), la función comienza a disminuir hasta el punto (4, 2), donde termina la función.$

En los ejercicios 36 a 39, para cada una de las funciones definidas poco a poco,

a. evaluar a los valores dados de la variable independiente, y

b. bosquejar la gráfica.

36)$f(x)=\begin{cases}4x+3, & &\text{if } x≤0\\ -x+1, & &\text{if } x>0\end{cases} ;\quad f(−3);\; f(0);\; f(2)$

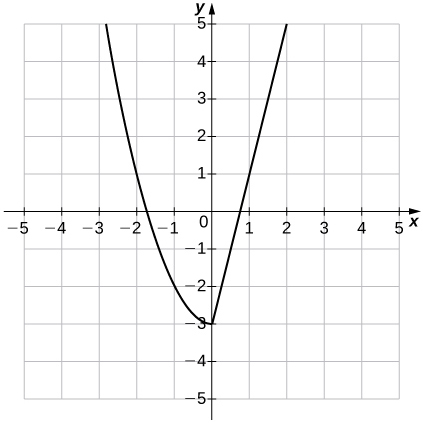
37)$f(x)=\begin{cases}x^2-3, & &\text{if } x≤0\\ 4x-3, & &\text{if } x>0\end{cases} ;\quad f(−4);\; f(0);\; f(2)$

Contestar

a.$f(−4) = 13,\quad f(0)=−3,\quad f(2)=5$

$Una imagen de una gráfica. El eje x va de -5 a 5 y el eje y va de -5 a 5. La gráfica es de una función que tiene dos piezas. La primera pieza es una curva decreciente que termina en el punto (0, -3). La segunda pieza es una línea creciente que comienza en el punto (0, -3). La función tiene una x intercepta en el punto aproximado (1.7, 0) y el punto (0.75, 0) y una intercepción y en (0, -3).$

38)$h(x)=\begin{cases}x+1, & &\text{if }x≤5\\4, & &\text{if } x>5\end{cases} ;\quad h(0);\; h(π);\; h(5)$

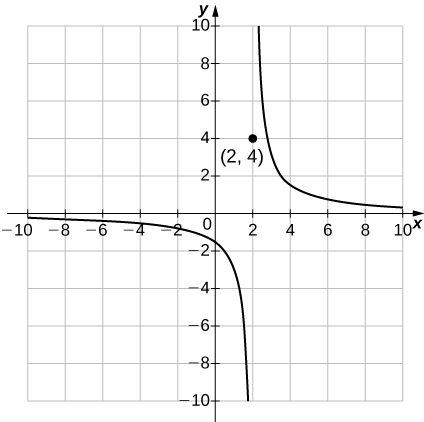
39)$g(x)=\begin{cases}\dfrac{3}{x−2}, & &\text{if }x≠2\\4, & &\text{if } x=2\end{cases} ;\quad g(0);\; g(−4);\; g(2)$

Contestar

a.$g(0) = -\frac{3}{2},\; g(-4)=-\frac{1}{2},\; g(2)=4$

$Una imagen de una gráfica. El eje x va de -10 a 10 y el eje y va de -10 a 10. La gráfica es de una función que comienza ligeramente por debajo del eje x y comienza a disminuir. A medida que la función se acerca a la línea vertical no trazada de “x = 2”, disminuye a un ritmo más rápido pero nunca llega a la línea “x = 2”. En el lado derecho de la línea no trazada “x = 2”, la función comienza en la parte superior de la gráfica y comienza a disminuir y se acerca a la línea horizontal no trazada “y = 0”, pero nunca alcanza “y = 0”. Allí función también incluye un punto trazado en (2, 4). Hay una intercepción y en (0, -1.5) y ninguna intercepción x.$

En los ejercicios 40 - 44, determinar si la afirmación es verdadera o falsa. Explique por qué.

40)$f(x)=\dfrac{4x+1}{7x−2}$ es una función trascendental.

41)$g(x)=\sqrt[3]{x}$ es una función raíz impar.

Contestar: Cierto;$n=3$

42) Una función logarítmica es una función algebraica.

43) Una función de la forma$f(x)=x^b$, donde$b$ es una constante valorada real, es una función exponencial.

Contestar: False;$f(x)=x^b$, donde$b$ es una constante de valor real, es una función de potencia

44) El dominio de una función raíz par es todo números reales.

45) [T] Una empresa compra algunos equipos de cómputos por $20,500. Al término de un periodo de 3 años, el valor del equipo ha disminuido linealmente a $12,301.

a. encontrar una función$y=V(t)$ que determine el valor$V$ del equipo al final de los$t$ años.

b. Encontrar e interpretar el significado de las$x$ - y$y$ -intercepciones para esta situación.

c. ¿Cuál es el valor del equipo al término de 5 años?

d. ¿Cuándo será el valor del equipo $3000?

Contestar: a.$V(t)=−2733t+20500$
b.$(0,20,500)$ significa que el precio de compra inicial del equipo es de 20.500 dólares;$(7.5,0)$ significa que en$7.5$ años el equipo de cómputos no tiene valor alguno.
c. $6835
d. En$6.4$ años aproximadamente

46) [T] El total de compras en línea durante las vacaciones navideñas ha aumentado dramáticamente durante los últimos 5 años. En 2012$(t=0)$, las ventas totales de vacaciones en línea fueron de 42.300 millones de dólares, mientras que en 2013 fueron de 48.100 millones de dólares.

a. Encontrar una función lineal$S$ que estime el total de ventas de vacaciones en línea en el año$t.$

b. Interpretar la pendiente de la gráfica de$S.$

c. Utilice la parte a. para predecir el año en que las compras en línea durante la Navidad alcanzarán los 60 mil millones de dólares.

47) [T] Una panadería familiar hace cupcakes y los vende en festivales locales al aire libre. Para un festival de música, hay un costo fijo de 125 dólares para montar un puesto para cupcakes. El dueño estima que cuesta $0.75 hacer cada cupcake. El propietario está interesado en determinar el costo$C$ total en función del número de cupcakes elaborados.

a. encontrar una función lineal que relacione el costo$C$ con$x,$ el número de cupcakes elaborados.

b. encontrar el costo de hornear$160$ magdalenas.

c. Si el dueño vende los cupcakes por $1.50 cada uno, ¿cuántos cupcakes necesita vender para comenzar a obtener ganancias? (Sugerencia: Use la función INTERSECCIÓN en una calculadora para encontrar este número.)

Contestar: a.$C=0.75x+125$
b. $245
c.$167$ magdalenas

48) [T] Se espera que una casa comprada por 250.000 dólares valga el doble de su precio de compra en 18 años.

a. encontrar una función lineal que modele el precio$P$ de la casa versus el número de años$t$ desde la compra original.

b. Interpretar la pendiente de la gráfica de$P.$

c. Encuentra el precio de la casa$15$ años desde que fue comprada originalmente.

49) [T] Se compró un automóvil por 26,000 dólares. El valor del automóvil se depreció en 1500 dólares anuales.

a. encontrar una función lineal que modele el valor$V$ del automóvil después de$t$ años.

b. Encontrar e interpretar$V(4)$.

Contestar: a.$V(t)=−1500t+26,000$
b. En$4$ años, el valor del automóvil es de 20,000 dólares.

50) [T] Un condominio en una parte de lujo de la ciudad fue comprado por $432,000. En$35$ años vale 60,500 dólares. Encuentra la tasa de depreciación.

51) [T] El costo total$C$ (en miles de dólares) para producir un determinado artículo es modelado por la función$C(x)=10.50x+28,500$, donde$x$ está el número de artículos producidos. Determinar el costo para producir$175$ artículos.

Contestar: $30,337,500

52) [T] Un profesor le pide a su clase que informe la cantidad de tiempo$t$ que dedicaron a escribir dos tareas. La mayoría de los estudiantes informan que les toma unos$45$ minutos escribir una tarea de cuatro páginas y aproximadamente$1.5$ horas escribir una tarea de nueve páginas.

a. encontrar la función lineal$y=N(t)$ que modela esta situación, donde$N$ es el número de páginas mecanografiadas y$t$ es el tiempo en minutos.

b. Utilice la parte a. para determinar cuántas páginas se pueden escribir en$2$ horas.

c. Utilice la parte a. para determinar cuánto tiempo se tarda en escribir una asignación de 20 páginas.

53) [T] La producción (como porcentaje de la capacidad total) de las centrales nucleares en Estados Unidos puede ser modelada por la función$P(t)=1.8576t+68.052$, donde$t$ es tiempo en años y$t=0$ corresponde a principios de 2000. Utilice el modelo para predecir el porcentaje de producción en 2015.

Contestar: 96% de la capacidad total

54) [T] La oficina de admisiones de una universidad pública estima que el 65% de los estudiantes a los que se les ofreció admisión a la clase de 2019 se inscribirán realmente.

a. encontrar la función lineal$y=N(x)$, donde$N$ es el número de alumnos que realmente se inscriben y$x$ es el número de todos los estudiantes que se ofrecen admisión a la clase de 2019.

b. Si la universidad quiere que el tamaño de la clase de primer año 2019 sea 1350, determine cuántos estudiantes deben ser admitidos.

Colaboradores

Template:ContribOpenStaxCalc