1.4E: Ejercicios para la Sección 1.4
- Page ID
- 116814
En los ejercicios 1 - 6, utilice la prueba de líneas horizontales para determinar si cada una de las gráficas dadas es uno a uno.
1)
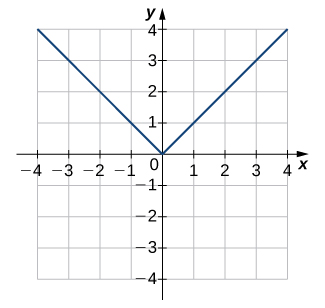
- Contestar
- No uno a uno
2)
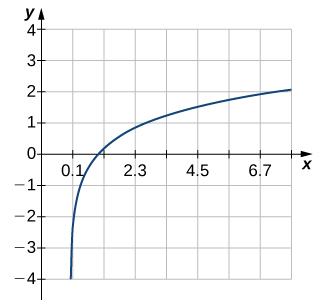
3)
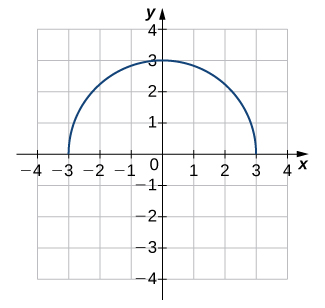
- Contestar
- No uno a uno
4)
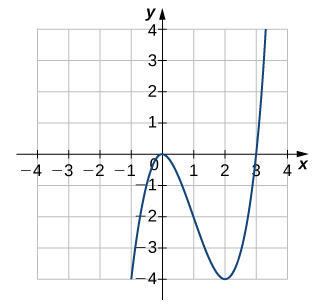
5)
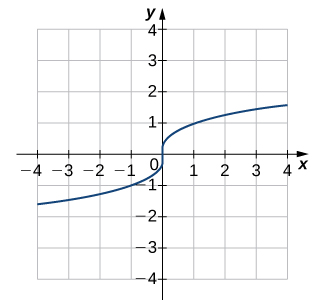
- Contestar
- Uno a uno
6)
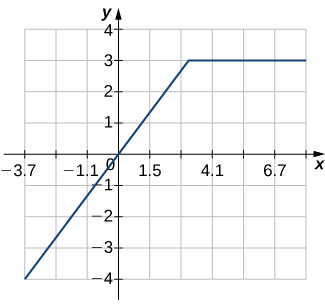
En los ejercicios 7 a 12,
a. encontrar la función inversa, y
b. encontrar el dominio y el rango de la función inversa.
7)\(f(x)=x^2−4, \quad x≥0\)
- Contestar
- a.\(f^{−1}(x)=\sqrt{x+4}\)
b. Dominio:\(x≥−4,\) Rango:\(y≥0\)
8)\(f(x)=\sqrt[3]{x−4}\)
9)\(f(x)=x^3+1\)
- Contestar
- a.\(f^{−1}(x)=\sqrt[3]{x−1}\)
b. Dominio: todos los números reales, Rango: todos los números reales
10)\(f(x)=(x−1)^2, \quad x≤1\)
11)\(f(x)=\sqrt{x−1}\)
- Contestar
- a.\(f^{−1}(x)=x^2+1\),
b. Dominio:\(x≥0,\) Rango:\(y≥1\)
12)\(f(x)=\dfrac{1}{x+2}\)
En los ejercicios 13 - 16, utilice la gráfica de\(f\) para bosquejar la gráfica de su función inversa.
13)
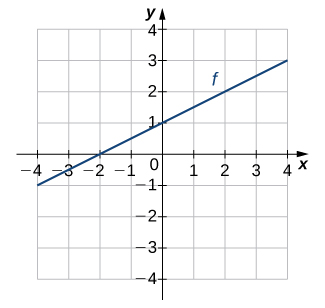
- Contestar
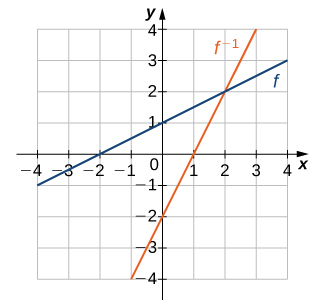
14)
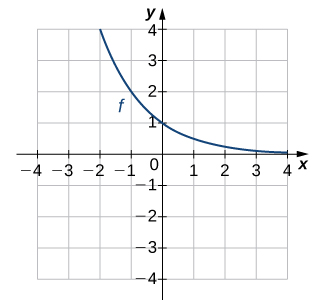
15)
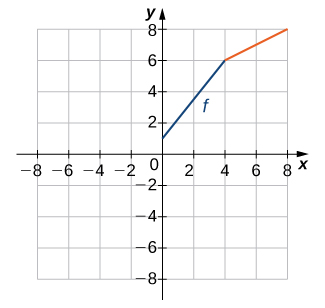
- Contestar
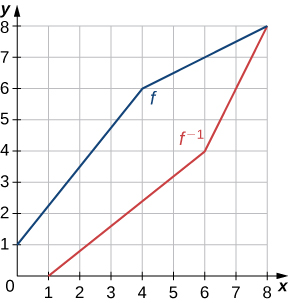
16)
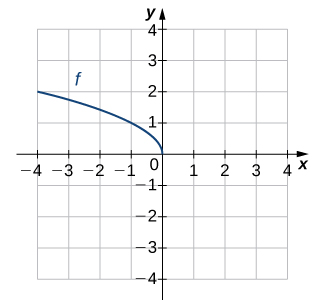
En los ejercicios 17 - 24, utilice la composición para determinar qué pares de funciones son inversas.
17)\(f(x)=8x, \quad g(x)=\dfrac{x}{8}\)
- Contestar
- Estas son inversas.
18)\(f(x)=8x+3, \quad g(x)=\dfrac{x-3}{8}\)
19)\(f(x)=5x−7, \quad g(x)=\dfrac{x+5}{7}\)
- Contestar
- Estas no son inversas.
20)\(f(x)=\frac{2}{3}x+2, \quad g(x)=\frac{3}{2}x+3\)
21)\(f(x)=\dfrac{1}{x−1}, \;x≠1, \quad g(x)=\dfrac{1}{x}+1,\; x≠0\)
- Contestar
- Estas son inversas.
22)\(f(x)=x^3+1,\quad g(x)=(x−1)^{1/3}\)
23)\(f(x)=x^2+2x+1,\; x≥−1, \quad g(x)=−1+\sqrt{x},\; x≥0\)
- Contestar
- Estas son inversas.
24)\(f(x)=\sqrt{4−x^2},\; 0≤x≤2, \quad g(x)=\sqrt{4−x^2},\; 0≤x≤2\)
En los ejercicios 25 - 33, evaluar las funciones. Dar el valor exacto.
25)\(\tan^{−1}\left(\frac{\sqrt{3}}{3}\right)\)
- Contestar
- \(\frac{π}{6}\)
26)\(\cos^{−1}\left(−\frac{\sqrt{2}}{2}\right)\)
27)\(\cot^{−1}(1)\)
- Contestar
- \(\frac{π}{4}\)
28)\(\sin^{−1}(−1)\)
29)\(\cos^{−1}\left(\frac{\sqrt{3}}{2}\right)\)
- Contestar
- \(\frac{π}{6}\)
30)\(\cos\big(\tan^{−1}(\sqrt{3})\big)\)
31)\(\sin\left(\cos^{−1}\left(\frac{\sqrt{2}}{2}\right)\right)\)
- Contestar
- \(\frac{\sqrt{2}}{2}\)
32)\(\sin^{−1}\left(\sin\left(\frac{π}{3}\right)\right)\)
33)\(\tan^{−1}\left(\tan\left(−\frac{π}{6}\right)\right)\)
- Contestar
- \(-\frac{π}{6}\)
34) La función\(C=T(F)=(5/9)(F−32)\) convierte grados Fahrenheit a grados Celsius.
a) Encontrar la función inversa\(F=T^{−1}(C)\)
b) ¿Para qué se utiliza la función inversa?
35) [T] La velocidad\(V\) (en centímetros por segundo) de la sangre en una arteria a una distancia\(x\) cm del centro de la arteria puede ser modelada por la función\(V=f(x)=500(0.04−x^2)\) para\(0≤x≤0.2.\)
a) Encontrar\(x=f^{−1}(V).\)
b) Interpretar para qué se utiliza la función inversa.
c) Encontrar la distancia desde el centro de una arteria con una velocidad de 15 cm/s, 10 cm/s y 5 cm/s.
- Contestar
- a.\(x=f^{−1}(V)=\sqrt{0.04−\dfrac{V}{500}}\)
b. La función inversa determina la distancia desde el centro de la arteria a la que fluye la sangre con velocidad\(V.\)
c. 0.1 cm; 0.14 cm; 0.17 cm
36) Una función que convierte las tallas de vestido en Estados Unidos a las de Europa viene dada por\(D(x)=2x+24.\)
a) Encuentra las tallas de vestidos europeos que corresponden a las tallas 6, 8, 10 y 12 en Estados Unidos.
b) Encuentra la función que convierte las tallas de vestidos europeos a tallas de vestido estadounidenses.
c) Usa la parte b. para encontrar las tallas de vestido en Estados Unidos que corresponden a 46, 52, 62 y 70.
37) [T] El costo de eliminar una toxina de un lago está modelado por la función\(C(p)=\dfrac{75p}{85−p},\) donde\(C\) está el costo (en miles de dólares) y\(p\) es la cantidad de toxina en un lago pequeño (medida en partes por mil millones [ppb]). Este modelo es válido sólo cuando la cantidad de toxina es inferior a 85 ppb.
a) Encontrar el costo de eliminar 25 ppb, 40 ppb y 50 ppb de la toxina del lago.
b) Encontrar la función inversa.
c) Utilizar la parte b. para determinar cuánto de la toxina se elimina por $50,000.
- Contestar
- a. $31,250, $66,667, $107,143
b.\(p=\dfrac{85C}{C+75}\)
c. 34 ppb
38) [T] Un auto de carreras está acelerando a una velocidad dada por\(v(t)=\frac{25}{4}t+54,\)
donde\(v\) esta la velocidad (en pies por segundo) en el tiempo\(t.\)
a) Encuentra la velocidad del carro a 10 seg.
b) Encontrar la función inversa.
c) Utilice la parte b. para determinar cuánto tiempo tarda el automóvil en alcanzar una velocidad de 150 pies/seg.
39) [T] El número Mach de un avión\(M\) es la relación entre su velocidad y la velocidad del sonido. Cuando un avión está volando a una altitud constante, entonces su ángulo Mach viene dado por\(μ=2\sin^{−1}\left(\frac{1}{M}\right).\)
Encuentra el ángulo Mach (al grado más cercano) para los siguientes números de Mach.
1.0”." style="width: 465px; height: 305px;" width="465px" height="305px" src="https://math.libretexts.org/@api/dek...01_04_215.jpeg">
a.\(μ=1.4\)
b.\(μ=2.8\)
c.\(μ=4.3\)
- Contestar
- a.\(\sim 92°\) b.\(\sim 42°\) c.\(\sim 27°\)
40) [T] Usando\(μ=2\sin^{−1}\left(\frac{1}{M}\right)\), encuentre el número Mach M para los siguientes ángulos.
a.\(μ=\frac{π}{6}\)
b.\(μ=\frac{2π}{7}\)
c.\(μ=\frac{3π}{8}\)
41) [T] La temperatura (en grados Celsius) de una ciudad en el norte de Estados Unidos puede ser modelada por la función
\(T(x)=5+18\sin\left[\frac{π}{6}(x−4.6)\right],\)
donde\(x\) es tiempo en meses y\(x=1.00\) corresponde al 1 de enero. Determinar el mes y el día en que la temperatura es\(21°C.\)
- Contestar
- \(x≈6.69,\, 8.51\); así, la temperatura ocurre el 21 de junio y 15 de agosto
42) [T] La profundidad (en pies) del agua en un muelle cambia con la subida y caída de las mareas. Está modelado por la función\(D(t)=5\sin\left(\frac{π}{6}t−\frac{7π}{6}\right)+8,\) donde\(t\) está el número de horas después de la medianoche. Determine la primera vez después de la medianoche cuando la profundidad es\(11.75\) ft.
43) [T] Un objeto que se mueve en movimiento armónico simple es modelado por la función\(s(t)=−6\cos\left(\dfrac{πt}{2}\right),\) donde\(s\) se mide en pulgadas y\(t\) se mide en segundos. Determine la primera vez en la que se encuentra\(4.5\) la distancia movida.
- Contestar
- \(\sim 1.5\)sec
44) [T] Una galería de arte local tiene un retrato de 3 pies de altura que se cuelga 2.5 pies por encima del nivel de los ojos de una persona promedio. El ángulo de visión\(θ\) puede ser modelado por la función\(θ=\tan^{−1}\frac{5.5}{x}−\tan^{−1}\frac{2.5}{x}\), donde\(x\) está la distancia (en pies) desde el retrato. Encuentra el ángulo de visión cuando una persona está a 4 pies del retrato.
45) [T] Utilice una calculadora para evaluar\(\tan^{−1}(\tan(2.1))\) y\(\cos^{−1}(\cos(2.1))\). Explicar los resultados de cada uno.
- Contestar
- \(\tan^{−1}(\tan(2.1))≈−1.0416\); la expresión no es igual\(2.1\) ya que\(2.1>1.57=\frac{π}{2}\) —en otras palabras, no está en el dominio restringido de\(\tan x\). \(\cos^{−1}(\cos(2.1))=2.1\), ya que\(2.1\) está en el dominio restringido de\(\cos x\).
46) [T] Utilice una calculadora para evaluar\(\sin(\sin^{−1}(−2))\) y\(\tan(\tan^{−1}(−2))\). Explicar los resultados de cada uno.


