1.5E: Ejercicios para la Sección 1.5

Última actualización
Guardar como PDF

Page ID: 116788

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En los ejercicios 1 - 4, evalúe las funciones exponenciales dadas como se indica, con precisión a dos dígitos significativos después del decimal.

1)$f(x)=5^x$

a.$x=3$

b.$x=\frac{1}{2}$

c.$x=\sqrt{2}$

Responder: a.$125$
b.$2.24$
c.$9.74$

2)$f(x)=(0.3)^x$

a.$x=−1$

b.$x=4$

c.$x=−1.5$

3)$f(x)=10^x$

a.$x=−2$

b.$x=4$

c.$x=\frac{5}{3}$

Responder: a.$0.01$
b.$10,000$
c.$46.42$

4)$f(x)=e^x$

a.$x=2$

b.$x=−3.2$

c.$x=π$

En los ejercicios 5 - 10, haga coincidir la ecuación exponencial con la gráfica correcta.

a.$y=4^{−x}$

b.$y=3^{x−1}$

c.$y=2^{x+1}$

d.$y=\left(\frac{1}{2}\right)^x+2$

e.$y=−3^{−x}$

f.$y=1−5^x$

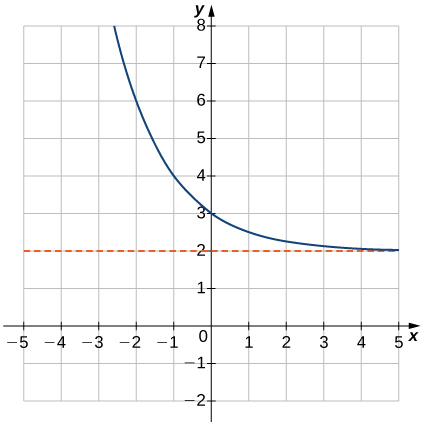
$Una imagen de una gráfica. El eje x va de -5 a 5 y el eje y va de -2 a 8. La gráfica es de una función curva decreciente. La función disminuye hasta que se acerca a la línea “y = 2”, pero nunca toca esta línea. La intercepción y está en el punto (0, 3) y no hay intercepción x.$

Responder: d

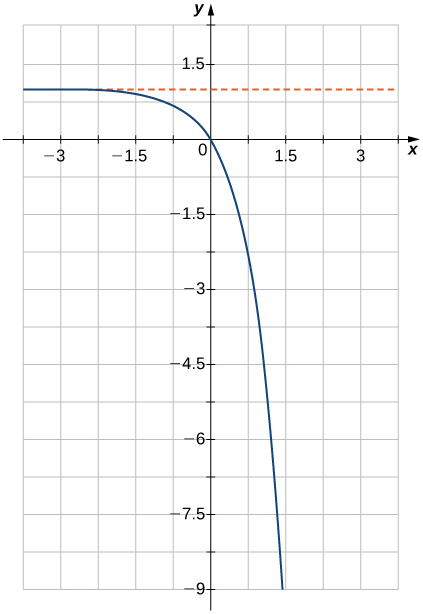
$Una imagen de una gráfica. El eje x va de -4 a 4 y el eje y va de -9 a 2. El gráfico es de una función que comienza ligeramente por debajo de la línea “y = 1” y comienza a disminuir rápidamente en una curva. La intercepción x y la intercepción y están ambas en el origen.$

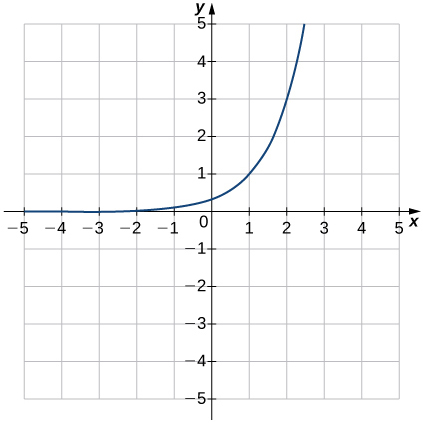
$Una imagen de una gráfica. El eje x va de -5 a 5 y el eje y va de -5 a 5. La gráfica es de una función creciente curvada que comienza ligeramente por encima del eje x y comienza a aumentar rápidamente. No hay intercepción x y la intercepción y está en el punto (0, (1/3)). Otro punto de la gráfica está en (1, 1).$

Responder: b

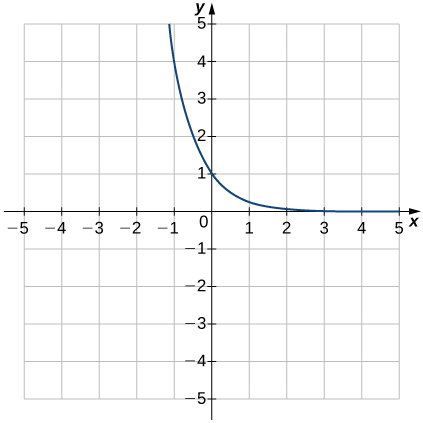
$Una imagen de una gráfica. El eje x va de -5 a 5 y el eje y va de -5 a 5. El gráfico es de una función decreciente curva que disminuye hasta que se acerca al eje x sin tocarlo. No hay intercepción x y la intercepción y está en el punto (0, 1). Otro punto de la gráfica está en (-1, 4).$

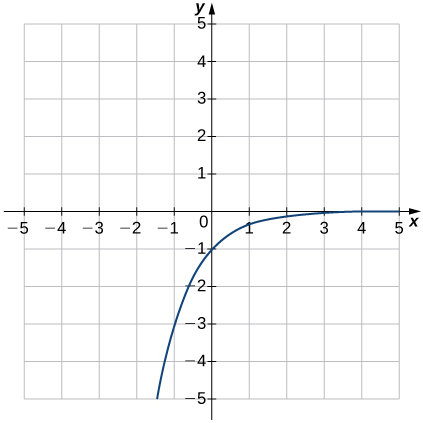
$Una imagen de una gráfica. El eje x va de -5 a 5 y el eje y va de -5 a 5. La gráfica es de una función creciente curvada que aumenta hasta que se acerca cerca del eje x sin tocarlo. No hay intercepción x y la intercepción y está en el punto (0, -1). Otro punto de la gráfica está en (-1, -3).$

Responder: e

10)

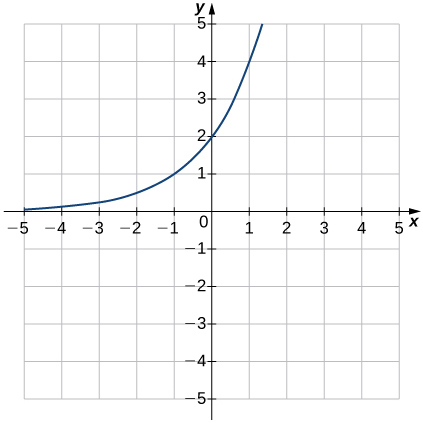
En los ejercicios 11 - 17, esboza la gráfica de la función exponencial. Determinar el dominio, el rango y la asíntota horizontal.

11)$f(x)=e^x+2$

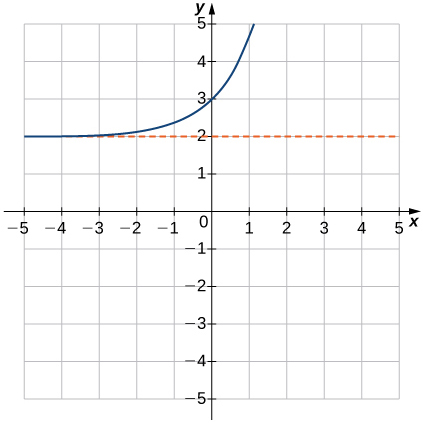
$Una imagen de una gráfica. El eje x va de -5 a 5 y el eje y va de -5 a 5. El gráfico es de una función creciente curva que comienza ligeramente por encima de la línea “y = 2” y comienza a aumentar rápidamente. No hay intercepción x y la intercepción y está en el punto (0, 3).$

Responder: Dominio: todos los números reales, Rango:$(2,∞),\; y=2$

12)$f(x)=−2^x$

$alt$

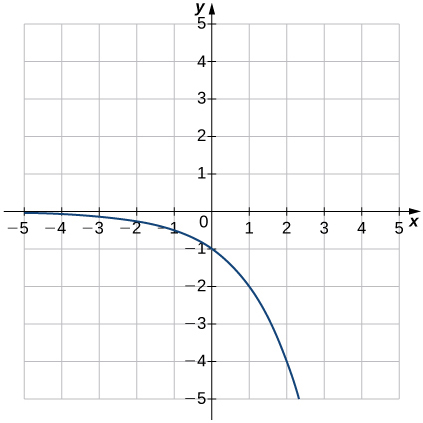
13)$f(x)=3^{x+1}$

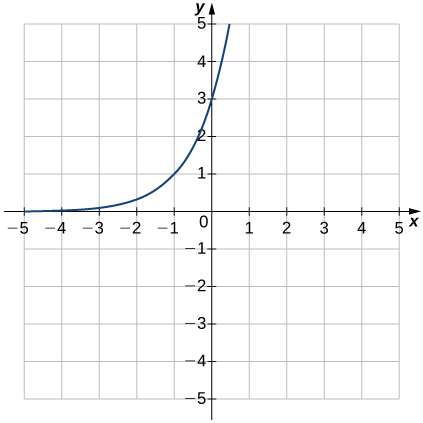
Responder: Dominio: todos los números reales, Rango:$(0,∞),\; y=0$

14)$f(x)=4^x−1$

$alt$

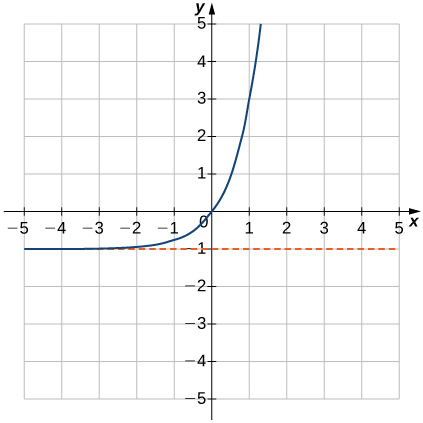
15)$f(x)=1−2^{−x}$

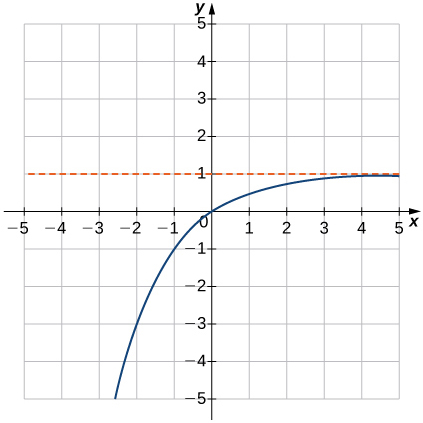
$Una imagen de una gráfica. El eje x va de -5 a 5 y el eje y va de -5 a 5. La gráfica es de una función creciente curvada que aumenta hasta que llega cerca de la línea “y = 1” sin tocarla. Allí x intercepción y la intercepción y están ambas en el origen. Otro punto de la gráfica está en (-1, -1).$

Responder: Dominio: todos los números reales, Rango:$(−∞,1),\; y=1$

16)$f(x)=5^{x+1}+2$

$alt$

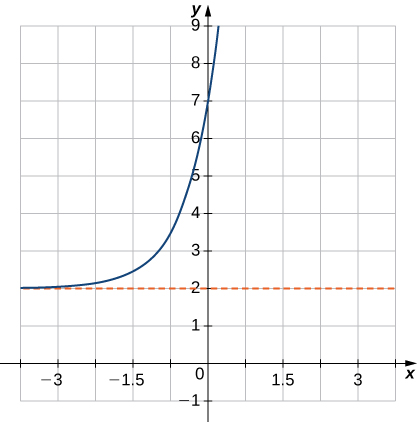
17)$f(x)=e^{−x}−1$

$Una imagen de una gráfica. El eje x va de -5 a 5 y el eje y va de -5 a 5. La gráfica es de una función decreciente curva que disminuye hasta que llega cerca de la línea “y = -1” sin tocarla. Allí x intercepción y la intercepción y están ambas en el origen. Hay un punto aproximado en la gráfica en (-1, 1.7).$

Responder: Dominio: todos los números reales, Rango:$(−1,∞), \;y=−1$

En los ejercicios 18 - 25, escriba la ecuación en forma exponencial equivalente.

18)$\log_3 81=4$

19)$\log_8 2=\frac{1}{3}$

Responder: $8^{1/3}=2$

20)$\log_5 1=0$

21)$\log_5 25=2$

Responder: $5^2=25$

22)$\log 0.1=−1$

23)$\ln\left(\frac{1}{e^3}\right)=−3$

Responder: $e^{−3}=\dfrac{1}{e^3}$

24)$\log_9 3=0.5$

25)$\ln 1=0$

Responder: $e^0=1$

En los ejercicios 26 - 35, escriba la ecuación en forma logarítmica equivalente.

26)$2^3=8$

27)$4^{−2}=\frac{1}{16}$

Responder: $\log_4\left(\frac{1}{16}\right)=−2$

28)$10^2=100$

29)$9^0=1$

Responder: $\log_9 1=0$

30)$\left(\frac{1}{3}\right)^3=\frac{1}{27}$

31)$\sqrt[3]{64}=4$

Responder: $\log_{64}4=\frac{1}{3}$

32)$e^x=y$

33)$9^y=150$

Responder: $\log_9 150=y$

34)$b^3=45$

35)$4^{-3/2}=0.125$

Responder: $\log_4 0.125=−\frac{3}{2}$

En los ejercicios 36 - 41, esboza la gráfica de la función logarítmica. Determinar el dominio, el rango y la asíntota vertical.

36)$f(x)=3+\ln x$

$alt$

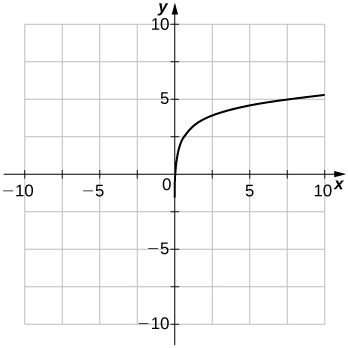
37)$f(x)=\ln(x−1)$

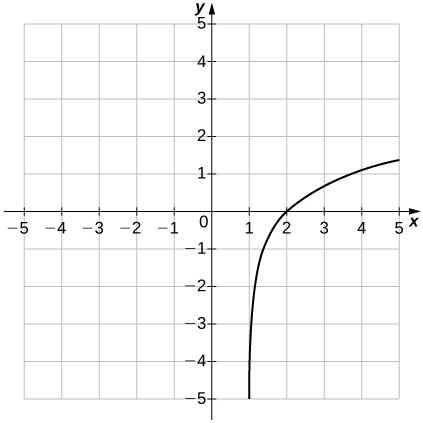
$Una imagen de una gráfica. El eje x va de -5 a 5 y el eje y va de -5 a 5. La gráfica es de una función curva creciente que comienza ligeramente a la derecha de la línea vertical “x = 1”. No hay intercepción y y la intercepción x está en el punto aproximado (2, 0).$

Responder: Dominio:$(1,∞)$, Rango:$(−∞,∞),\; x=1$

38)$f(x)=\ln(−x)$

$alt$

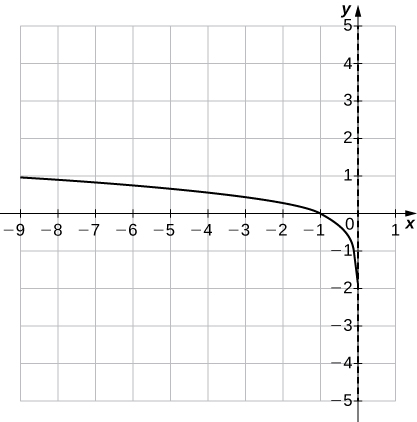
39)$f(x)=1−\ln x$

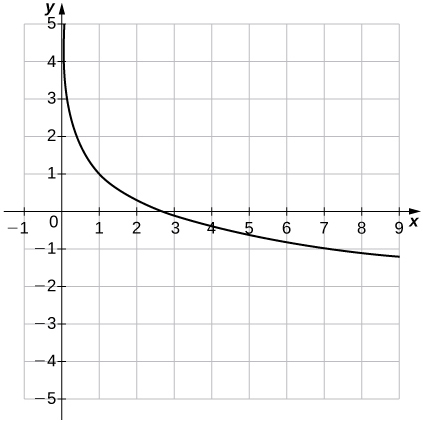
$Una imagen de una gráfica. El eje x va de -1 a 9 y el eje y va de -5 a 5. La gráfica es de una función curva decreciente que comienza ligeramente a la derecha del eje y. No hay intercepción y y la intercepción x está en el punto (e, 0).$

Responder: Dominio:$(0,∞)$, Rango:$(−∞,∞),\; x=0$

40)$f(x)=\log x−1$

$221$

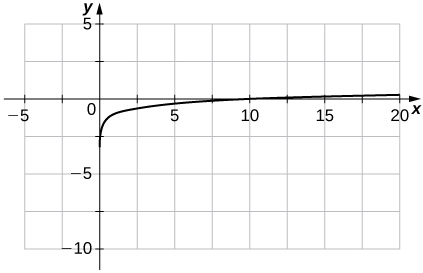
41)$f(x)=\ln(x+1)$

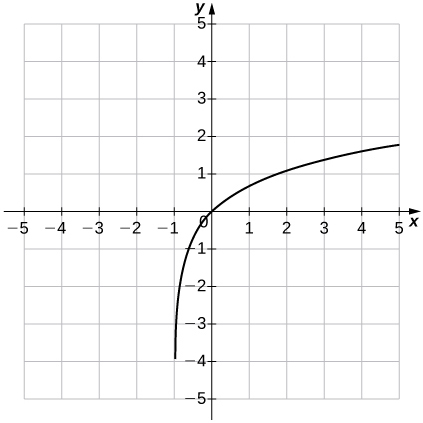
$Una imagen de una gráfica. El eje x va de -5 a 5 y el eje y va de -5 a 5. La gráfica es de una función curva creciente que comienza ligeramente a la derecha de la línea vertical “x = -1”. Allí y intercepción y la intercepción x están ambas en el origen.$

Responder: Dominio:$(−1,∞)$, Rango:$(−∞,∞)$,$x=−1$

En los ejercicios 42 - 47, usa propiedades de logaritmos para escribir las expresiones como suma, diferencia y/o producto de logaritmos.

42)$\log x^4y$

43)$\log_3\frac{9a^3}{b}$

Responder: $2+3\log_3 a−\log_3 b$

44)$\ln a\sqrt[3]{b}$

45)$\log_5\sqrt{125xy^3}$

Responder: $\frac{3}{2}+\frac{1}{2}\log_5 x+\frac{3}{2}\log_5 y$

46)$\log_4 \frac{\sqrt[3]{xy}}{64}$

47)$\ln\left(\frac{6}{\sqrt{e^3}}\right)$

Responder: $−\frac{3}{2}+\ln 6$

En los ejercicios 48 - 55, resuelve exactamente la ecuación exponencial.

48)$5^x=125$

49)$e^{3x}−15=0$

Responder: $\frac{\ln 15}{3}$

50)$8^x=4$

51)$4^{x+1}−32=0$

Responder: $\frac{3}{2}$

52)$3^{x/14}=\frac{1}{10}$

53)$10^x=7.21$

Responder: $\log 7.21$

54)$4⋅2^{3x}−20=0$

55)$7^{3x−2}=11$

Contestar: $\frac{2}{3}+\frac{\log 11}{3\log 7}$

En los ejercicios 56 - 63, resuelve la ecuación logarítmica exactamente, si es posible.

56)$\log_3 x=0$

57)$\log_5 x=−2$

Contestar: $x=\frac{1}{25}$

58)$\log_4(x+5)=0$

59)$\log(2x−7)=0$

Contestar: $x=4$

60)$\ln\sqrt{x+3}=2$

61)$\log_6(x+9)+\log_6 x=2$

Contestar: $x=3$

62)$\log_4(x+2)−\log_4(x−1)=0$

63)$\ln x+\ln(x−2)=\ln 4$

Contestar: $1+\sqrt{5}$

En los ejercicios 64 - 69, utilice la fórmula de cambio de base y ya sea base$10$ o base$e$ para evaluar las expresiones dadas. Contestar en forma exacta y en forma aproximada, redondeando a cuatro decimales.

64)$\log_5 47$

65)$\log_7 82$

Contestar: $\dfrac{\log 82}{\log 7}≈2.2646$

66)$\log_6 103$

67)$\log_{0.5}211$

Contestar: $\dfrac{\log 211}{\log 0.5}≈−7.7211$

68)$\log_2 π$

69)$\log_{0.2}0.452$

Contestar: $\dfrac{\log 0.452}{\log 0.2}≈0.4934$

70) Reescribir las siguientes expresiones en términos de exponenciales y simplificar.

a.$2\cosh(\ln x)$ b.$\cosh 4x+\sinh 4x$ c.$\cosh 2x−\sinh 2x$ d.$\ln(\cosh x+\sinh x)+\ln(\cosh x−\sinh x)$

71) [T] El número de bacterias$N$ en un cultivo después de$t$ días puede ser modelado por la función$N(t)=1300⋅(2)^{t/4}$. Encuentra el número de bacterias presentes después de$15$ días.

Contestar: $\sim 17,491$

72) [T] La demanda$D$ (en millones de barriles) de petróleo en un país rico en petróleo viene dada por la función$D(p)=150⋅(2.7)^{−0.25p}$, donde$p$ está el precio (en dólares) de un barril de petróleo. Encuentra la cantidad de petróleo que se demanda (al millón de barriles más cercano) cuando el precio esté entre $15 y $20.

73) [T] El monto$A$ de una inversión de $100,000 pagando continuamente y compuesta por t años viene dado por$A(t)=100,000⋅e^{0.055t}$. Encuentra la cantidad$A$ acumulada en$5$ años.

Contestar: Aproximadamente $131,653 se acumula en 5 años.

74) [T] Una inversión se compone mensual, trimestral o anual y viene dada por la función$A=P\left(1+\frac{j}{n}\right)^{nt}$, donde$A$ está el valor de la inversión en el momento$t$,$P$ es el principio inicial que se invirtió,$j$ es la tasa de interés anual, y$n$ es el número de tiempo el interés se compone por año. Dada una tasa de interés anual de 3.5% y un principio inicial de $100,000, encuentra el monto$A$ acumulado en 5 años por intereses que se compone a. diario, b., mensual, c. trimestral, y d. anual.

75) [T] La concentración de iones hidrógeno en una sustancia se denota por$[H+]$, medida en moles por litro. El pH de una sustancia se define por la función logarítmica$pH=−\log[H+]$. Esta función se utiliza para medir la acidez de una sustancia. El pH del agua es 7. Una sustancia con un pH menor a 7 es un ácido, mientras que una que tiene un pH superior a 7 es una base.

a. Encontrar el pH de las siguientes sustancias. Redondear las respuestas a un dígito.

b. Determinar si la sustancia es un ácido o una base.

i. Huevos:$[H+]=1.6×10^{−8}$ mol/L

ii. Cerveza:$[H+]=3.16×10^{−3}$ mol/L

iii. Jugo de Tomate:$[H+]=7.94×10^{−5}$ mol/l

Contestar: i. a. pH = 8 b. Base
ii. a. pH = 3 b. Ácido
iii. a. pH = 4 b. Ácido

76) [T] El yodo-131 es una sustancia radiactiva que se descompone según la función$Q(t)=Q_0⋅e^{−0.08664t}$, donde$Q_0$ está la cantidad inicial de una muestra de la sustancia y$t$ es en días. Determinar cuánto tiempo tarda (al día más cercano) el 95% de una cantidad en decairse.

77) [T] Según el Banco Mundial, a finales de 2013$(t=0)$ la población estadounidense era de 316 millones y estaba aumentando según el siguiente modelo:

\[P(t)=316e^{0.0074t}, \nonumber \]

donde$P$ se mide en millones de personas y$t$ se mide en años posteriores a 2013.

a. Con base en este modelo, ¿cuál será la población de Estados Unidos en 2020?

b. Determinar cuándo la población estadounidense será el doble de lo que es en 2013.

Contestar: a.$\sim 333$ millones
b. 94 años a partir de 2013, o en 2107

78) [T] La cantidad$A$ acumulada después de que los$1000$ dólares se inviertan por$t$ años a una tasa de interés del 4% es modelada por la función$A(t)=1000(1.04)^t$.

a. Encontrar la cantidad acumulada después de$5$ años y$10$ años.

b. Determinar el tiempo que tarda en triplicarse la inversión original.

79) [T] Se sabe que una colonia bacteriana cultivada en un laboratorio se duplica en número en$12$ horas. Supongamos, inicialmente, que hay$1000$ bacterias presentes.

a. Utilizar la función exponencial$Q=Q_0e^{kt}$ para determinar el valor$k$, que es la tasa de crecimiento de la bacteria. Redondear a cuatro decimales.

b. Determinar aproximadamente cuánto tiempo tarda en crecer$200,000$ las bacterias.

Contestar: a.$k≈0.0578$
b. ≈$92$ horas

80) [T] La población de conejos en una reserva de caza se duplica cada$6$ mes. Supongamos que inicialmente había$120$ conejos.

a. Utilice la función exponencial$P=P_0a^t$ para determinar la constante de la tasa de crecimiento$a$. Redondear a cuatro decimales.

b. utilizar la función en la parte a. para determinar aproximadamente cuánto tiempo tarda la población de conejos en llegar a 3500.

81) [T] El sismo de 1906 en San Francisco tuvo una magnitud de 8.3 en la escala de Richter. Al mismo tiempo, en Japón, un sismo de magnitud 4.9 causó sólo daños menores. Aproximadamente, ¿cuánta energía más liberó el terremoto de San Francisco que por el sismo japonés?

Contestar: El terremoto de San Francisco tuvo$10^{3.4}$ o$\sim 2512$ veces más energía que el terremoto de Japón.

Colaboradores

Template:ContribOpenStaxCalc