2.2E: Ejercicios para la Sección 2.2
- Page ID
- 116859
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Definición intuitiva de límites
Para los ejercicios 1 - 2, considere la función\(f(x)=\dfrac{x^2−1}{|x−1|}\).
1) [T] Complete la siguiente tabla para la función. Redondee sus soluciones a cuatro decimales.
| \(x\) | \(f(x)\) | \(x\) | \(f(x)\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">0.9 | \ (f (x)\)” style="text-align:center; ">a. | \ (x\)” style="text-align:center; ">1.1 | \ (f (x)\)” style="text-align:center; ">e. |
| \ (x\)” style="text-align:center; ">0.99 | \ (f (x)\)” style="text-align:center; ">b. | \ (x\)” style="text-align:center; ">1.01 | \ (f (x)\)” style="text-align:center; ">f. |
| \ (x\)” style="text-align:center; ">0.999 | \ (f (x)\)” style="text-align:center; ">c. | \ (x\)” style="text-align:center; ">1.001 | \ (f (x)\)” style="text-align:center; ">g. |
| \ (x\)” style="text-align:center; ">0.9999 | \ (f (x)\)” style="text-align:center; ">d. | \ (x\)” style="text-align:center; ">1.0001 | \ (f (x)\)” style="text-align:center; ">h. |
2) ¿Qué indican tus resultados en el ejercicio anterior sobre el límite de dos caras\(\displaystyle \lim_{x→1}f(x)\)? Explica tu respuesta.
- Responder
-
\(\displaystyle \lim_{x \to 1}f(x)\)no existe porque\(\displaystyle \lim_{x \to 1^−}f(x)=−2≠\lim_{x \to 1^+}f(x)=2\).
Para los ejercicios 3 - 5, considere la función\(f(x)=(1+x)^{1/x}\).
3) [T] Hacer una tabla que muestre los valores de\(f\) para\(x=−0.01,\;−0.001,\;−0.0001,\;−0.00001\) y para\(x=0.01,\;0.001,\;0.0001,\;0.00001\). Redondee sus soluciones a cinco decimales.
| \(x\) | \(f(x)\) | \(x\) | \(f(x)\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">-0.01 | \ (f (x)\)” style="text-align:center; ">a. | \ (x\)” style="text-align:center; ">0.01 | \ (f (x)\)” style="text-align:center; ">e. |
| \ (x\)” style="text-align:center; ">-0.001 | \ (f (x)\)” style="text-align:center; ">b. | \ (x\)” style="text-align:center; ">0.001 | \ (f (x)\)” style="text-align:center; ">f. |
| \ (x\)” style="text-align:center; ">-0.0001 | \ (f (x)\)” style="text-align:center; ">c. | \ (x\)” style="text-align:center; ">0.0001 | \ (f (x)\)” style="text-align:center; ">g. |
| \ (x\)” style="text-align:center; ">-0.00001 | \ (f (x)\)” style="text-align:center; ">d. | \ (x\)” style="text-align:center; ">0.00001 | \ (f (x)\)” style="text-align:center; ">h. |
4) ¿Qué indica la tabla de valores del ejercicio anterior sobre la función\(f(x)=(1+x)^{1/x}\)?
- Responder
- \(\displaystyle \lim_{x \to 0}(1+x)^{1/x}\approx 2.7183\).
5) ¿A qué constante matemática parecen acercarse los valores del ejercicio anterior? Este es el límite real aquí.
En los ejercicios 6 - 8, utilice los valores dados para configurar una tabla para evaluar los límites. Redondee sus soluciones a ocho decimales.
6) [T]\(\displaystyle \lim_{x \to 0}\frac{\sin 2x}{x};\quad ±0.1,\; ±0.01, \; ±0.001, \;±.0001\)
| \(x\) | \(\frac{\sin 2x}{x}\) | \(x\) | \(\frac{\sin 2x}{x}\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">-0.1 | \ (\ frac {\ sin 2x} {x}\)” style="text-align:center; ">a. | \ (x\)” style="text-align:center; ">0.1 | \ (\ frac {\ sin 2x} {x}\)” style="text-align:center; ">e. |
| \ (x\)” style="text-align:center; ">-0.01 | \ (\ frac {\ sin 2x} {x}\)” style="text-align:center; ">b. | \ (x\)” style="text-align:center; ">0.01 | \ (\ frac {\ sin 2x} {x}\)” style="text-align:center; ">f. |
| \ (x\)” style="text-align:center; ">-0.001 | \ (\ frac {\ sin 2x} {x}\)” style="text-align:center; ">c. | \ (x\)” style="text-align:center; ">0.001 | \ (\ frac {\ sin 2x} {x}\)” style="text-align:center; ">g. |
| \ (x\)” style="text-align:center; ">-0.0001 | \ (\ frac {\ sin 2x} {x}\)” style="text-align:center; ">d. | \ (x\)” style="text-align:center; ">0.0001 | \ (\ frac {\ sin 2x} {x}\)” style="text-align:center; ">h. |
- Responder
- a. 1.98669331; b. 1.99986667; c. 1.99999867; d. 1.99999999; e. 1.98669331; f. 1.99986667; g. 1.99999867; h. 1.99999999; h. 1.99999999;
\(\displaystyle \lim_{x \to 0}\frac{\sin 2x}{x}=2\)
7) [T]\(\displaystyle \lim_{x \to 0}\frac{\sin 3x}{x} ±0.1, \; ±0.01, \; ±0.001, \; ±0.0001\)
| \(x\) | \(\frac{\sin 3x}{x}\) | \(x\) | \(\frac{\sin 3x}{x}\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">-0.1 | \ (\ frac {\ sin 3x} {x}\)” style="text-align:center; ">a. | \ (x\)” style="text-align:center; ">0.1 | \ (\ frac {\ sin 3x} {x}\)” style="text-align:center; ">e. |
| \ (x\)” style="text-align:center; ">-0.01 | \ (\ frac {\ sin 3x} {x}\)” style="text-align:center; ">b. | \ (x\)” style="text-align:center; ">0.01 | \ (\ frac {\ sin 3x} {x}\)” style="text-align:center; ">f. |
| \ (x\)” style="text-align:center; ">-0.001 | \ (\ frac {\ sin 3x} {x}\)” style="text-align:center; ">c. | \ (x\)” style="text-align:center; ">0.001 | \ (\ frac {\ sin 3x} {x}\)” style="text-align:center; ">g. |
| \ (x\)” style="text-align:center; ">-0.0001 | \ (\ frac {\ sin 3x} {x}\)” style="text-align:center; ">d. | \ (x\)” style="text-align:center; ">0.0001 | \ (\ frac {\ sin 3x} {x}\)” style="text-align:center; ">h. |
8) Utilice los dos ejercicios anteriores para conjeturar (adivinar) el valor del siguiente límite:\(\displaystyle \lim_{x \to 0}\frac{\sin ax}{x}\) for\(a\), un valor real positivo.
- Responder
- \(\displaystyle \lim_{x \to 0}\frac{\sin ax}{x}=a\)
[T] En los ejercicios 9 - 14, establecer una tabla de valores para encontrar el límite indicado. Redondear a ocho dígitos significativos.
9)\(\displaystyle \lim_{x \to 2}\frac{x^2−4}{x^2+x−6}\)
| \(x\) | \(\frac{x^2−4}{x^2+x−6}\) | \(x\) | \(\frac{x^2−4}{x^2+x−6}\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">1.9 | \ (\ frac {x^2−4} {x^2+x−6}\)” style="text-align:center; ">a. | \ (x\)” style="text-align:center; ">2.1 | \ (\ frac {x^2−4} {x^2+x−6}\)” style="text-align:center; ">e. |
| \ (x\)” style="text-align:center; ">1.99 | \ (\ frac {x^2−4} {x^2+x−6}\)” style="text-align:center; ">b. | \ (x\)” style="text-align:center; ">2.01 | \ (\ frac {x^2−4} {x^2+x−6}\)” style="text-align:center; ">f. |
| \ (x\)” style="text-align:center; ">1.999 | \ (\ frac {x^2−4} {x^2+x−6}\)” style="text-align:center; ">c. | \ (x\)” style="text-align:center; ">2.001 | \ (\ frac {x^2−4} {x^2+x−6}\)” style="text-align:center; ">g. |
| \ (x\)” style="text-align:center; ">1.9999 | \ (\ frac {x^2−4} {x^2+x−6}\)” style="text-align:center; ">d. | \ (x\)” style="text-align:center; ">2.0001 | \ (\ frac {x^2−4} {x^2+x−6}\)” style="text-align:center; ">h. |
10)\(\displaystyle \lim_{x \to 1}(1−2x)\)
| \(x\) | \(1−2x\) | \(x\) | \(1−2x\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">0.9 | \ (1−2x\)” style="text-align:center; ">a. | \ (x\)” style="text-align:center; ">1.1 | \ (1−2x\)” style="text-align:center; ">e. |
| \ (x\)” style="text-align:center; ">0.99 | \ (1−2x\)” style="text-align:center; ">b. | \ (x\)” style="text-align:center; ">1.01 | \ (1−2x\)” style="text-align:center; ">f. |
| \ (x\)” style="text-align:center; ">0.999 | \ (1−2x\)” style="text-align:center; ">c. | \ (x\)” style="text-align:center; ">1.001 | \ (1−2x\)” style="text-align:center; ">g. |
| \ (x\)” style="text-align:center; ">0.9999 | \ (1−2x\)” style="text-align:center; ">d. | \ (x\)” style="text-align:center; ">1.0001 | \ (1−2x\)” style="text-align:center; ">h. |
- Responder
- a. −0.80000000; b. −0.98000000; c. −0.99800000; d. −0.99980000; e. −1.2000000; f. −1.0200000; g. −1.0020000; h. −1.0002000;
\( \displaystyle \lim_{x \to 1}(1−2x)=−1\)
11)\(\displaystyle \lim_{x \to 0}\frac{5}{1−e^{1/x}}\)
| \(x\) | \(\frac{5}{1−e^{1/x}}\) | \(x\) | \(\frac{5}{1−e^{1/x}}\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">-0.1 | \ (\ frac {5} {1−e^ {1/x}}\)” style="text-align:center; ">a. | \ (x\)” style="text-align:center; ">0.1 | \ (\ frac {5} {1−e^ {1/x}}\)” style="text-align:center; ">e. |
| \ (x\)” style="text-align:center; ">-0.01 | \ (\ frac {5} {1−e^ {1/x}}\)” style="text-align:center; ">b. | \ (x\)” style="text-align:center; ">0.01 | \ (\ frac {5} {1−e^ {1/x}}\)” style="text-align:center; ">f. |
| \ (x\)” style="text-align:center; ">-0.001 | \ (\ frac {5} {1−e^ {1/x}}\)” style="text-align:center; ">c. | \ (x\)” style="text-align:center; ">0.001 | \ (\ frac {5} {1−e^ {1/x}}\)” style="text-align:center; ">g. |
| \ (x\)” style="text-align:center; ">-0.0001 | \ (\ frac {5} {1−e^ {1/x}}\)” style="text-align:center; ">d. | \ (x\)” style="text-align:center; ">0.0001 | \ (\ frac {5} {1−e^ {1/x}}\)” style="text-align:center; ">h. |
12)\(\displaystyle \lim_{z \to 0}\frac{z−1}{z^2(z+3)}\)
| \(z\) | \(\frac{z−1}{z^2(z+3)}\) | \(z\) | \(\frac{z−1}{z^2(z+3)}\) |
|---|---|---|---|
| \ (z\)” style="text-align:center; ">-0.1 | \ (\ frac {z−1} {z^2 (z+3)}\)” style="text-align:center; ">a. | \ (z\)” style="text-align:center; ">0.1 | \ (\ frac {z−1} {z^2 (z+3)}\)” style="text-align:center; ">e. |
| \ (z\)” style="text-align:center; ">-0.01 | \ (\ frac {z−1} {z^2 (z+3)}\)” style="text-align:center; ">b. | \ (z\)” style="text-align:center; ">0.01 | \ (\ frac {z−1} {z^2 (z+3)}\)” style="text-align:center; ">f. |
| \ (z\)” style="text-align:center; ">-0.001 | \ (\ frac {z−1} {z^2 (z+3)}\)” style="text-align:center; ">c. | \ (z\)” style="text-align:center; ">0.001 | \ (\ frac {z−1} {z^2 (z+3)}\)” style="text-align:center; ">g. |
| \ (z\)” style="text-align:center; ">-0.0001 | \ (\ frac {z−1} {z^2 (z+3)}\)” style="text-align:center; ">d. | \ (z\)” style="text-align:center; ">0.0001 | \ (\ frac {z−1} {z^2 (z+3)}\)” style="text-align:center; ">h. |
- Responder
- a. −37.931034; b. −3377.9264; c. −333,777.93; d. −33,337,778; e. −29.032258; f. −3289.0365; g. −332,889.04; h. −33,328,889
\( \displaystyle \lim_{x \to 0}\frac{z−1}{z^2(z+3)}=−∞\)
13)\(\displaystyle \lim_{t \to 0^+}\frac{\cos t}{t}\)
| \(t\) | \(\frac{\cos t}{t}\) |
|---|---|
| \ (t\)” style="text-align:center; ">0.1 | \ (\ frac {\ cos t} {t}\)” style="text-align:center; ">a. |
| \ (t\)” style="text-align:center; ">0.01 | \ (\ frac {\ cos t} {t}\)” style="text-align:center; ">b. |
| \ (t\)” style="text-align:center; ">0.001 | \ (\ frac {\ cos t} {t}\)” style="text-align:center; ">c. |
| \ (t\)” style="text-align:center; ">0.0001 | \ (\ frac {\ cos t} {t}\)” style="text-align:center; ">d. |
14)\(\displaystyle \lim_{x \to 2}\frac{1−\frac{2}{x}}{x^2−4}\)
| \(x\) | \(\frac{1−\frac{2}{x}}{x^2−4}\) | \(x\) | \(\frac{1−\frac{2}{x}}{x^2−4}\) |
|---|---|---|---|
| \ (x\)” style="text-align:center; ">1.9 | \ (\ frac {1−\ frac {2} {x}} {x^2−4}\)” style="text-align:center; ">a. | \ (x\)” style="text-align:center; ">2.1 | \ (\ frac {1−\ frac {2} {x}} {x^2−4}\)” style="text-align:center; ">e. |
| \ (x\)” style="text-align:center; ">1.99 | \ (\ frac {1−\ frac {2} {x}} {x^2−4}\)” style="text-align:center; ">b. | \ (x\)” style="text-align:center; ">2.01 | \ (\ frac {1−\ frac {2} {x}} {x^2−4}\)” style="text-align:center; ">f. |
| \ (x\)” style="text-align:center; ">1.999 | \ (\ frac {1−\ frac {2} {x}} {x^2−4}\)” style="text-align:center; ">c. | \ (x\)” style="text-align:center; ">2.001 | \ (\ frac {1−\ frac {2} {x}} {x^2−4}\)” style="text-align:center; ">g. |
| \ (x\)” style="text-align:center; ">1.9999 | \ (\ frac {1−\ frac {2} {x}} {x^2−4}\)” style="text-align:center; ">d. | \ (x\)” style="text-align:center; ">2.0001 | \ (\ frac {1−\ frac {2} {x}} {x^2−4}\)” style="text-align:center; ">h. |
- Responder
- a. 0.13495277; b. 0.12594300; c. 0.12509381; d. 0.12500938; e. 0.11614402; f. 0.12406794; g. 0.12490631; h. 0.12499063;
\( \displaystyle ∴\lim_{x \to 2}\frac{1−\frac{2}{x}}{x^2−4}=0.1250=\frac{1}{8}\)
[T] En los ejercicios 15 - 16, establecer una tabla de valores y redondear a ocho dígitos significativos. Con base en la tabla de valores, hacer una conjetura sobre cuál es el límite. Luego, usa una calculadora para graficar la función y determinar el límite. ¿Fue correcta la conjetura? Si no, ¿por qué falla el método de las tablas?
15)\(\displaystyle \lim_{θ \to 0}\sin\left(\frac{π}{θ}\right)\)
| \(θ\) | \(\sin\left(\frac{π}{θ}\right)\) | \(θ\) | \(\sin\left(\frac{π}{θ}\right)\) |
|---|---|---|---|
| \ (θ\)” style="text-align:center; ">-0.1 | \ (\ sin\ left (\ frac {π} {θ}\ right)\)” style="text-align:center; ">a. | \ (θ\)” style="text-align:center; ">0.1 | \ (\ sin\ izquierda (\ frac {π} {θ}\ derecha)\)” style="text-align:center; ">e. |
| \ (θ\)” style="text-align:center; ">-0.01 | \ (\ sin\ izquierda (\ frac {π} {θ}\ derecha)\)” style="text-align:center; ">b. | \ (θ\)” style="text-align:center; ">0.01 | \ (\ sin\ left (\ frac {π} {θ}\ right)\)” style="text-align:center; ">f. |
| \ (θ\)” style="text-align:center; ">-0.001 | \ (\ sin\ izquierda (\ frac {π} {θ}\ derecha)\)” style="text-align:center; ">c. | \ (θ\)” style="text-align:center; ">0.001 | \ (\ sin\ left (\ frac {π} {θ}\ right)\)” style="text-align:center; ">g. |
| \ (θ\)” style="text-align:center; ">-0.0001 | \ (\ sin\ left (\ frac {π} {θ}\ right)\)” style="text-align:center; ">d. | \ (θ\)” style="text-align:center; ">0.0001 | \ (\ sin\ left (\ frac {π} {θ}\ right)\)” style="text-align:center; ">h. |
16)\(\displaystyle \lim_{α \to 0^+} \frac{1}{α}\cos\left(\frac{π}{α}\right)\)
| \(a\) | \(\frac{1}{α}\cos\left(\frac{π}{α}\right)\) |
|---|---|
| \ (a\)” style="text-align:center; ">0.1 | \ (\ frac {1} {α}\ cos\ izquierda (\ frac {π} {α}\ derecha)\)” style="text-align:center; ">a. |
| \ (a\)” style="text-align:center; ">0.01 | \ (\ frac {1} {α}\ cos\ izquierda (\ frac {π} {α}\ derecha)\)” style="text-align:center; ">b. |
| \ (a\)” style="text-align:center; ">0.001 | \ (\ frac {1} {α}\ cos\ izquierda (\ frac {π} {α}\ derecha)\)” style="text-align:center; ">c. |
| \ (a\)” style="text-align:center; ">0.0001 | \ (\ frac {1} {α}\ cos\ izquierda (\ frac {π} {α}\ derecha)\)” style="text-align:center; ">d. |
- Responder
-
a. 10.00000; b. 100.00000; c. 1000.0000; d. 10,000.000;
Adivina:\(\displaystyle \lim_{α→0^+}\frac{1}{α}\cos\left(\frac{π}{α}\right)=∞\);
Actual: DNE, ya que la gráfica muestra que la función oscila salvajemente entre valores que se acercan al infinito positivo y valores que se acercan al infinito negativo, a medida que se\(α\) acerca el valor de \(0\)desde el lado positivo.![Una gráfica de la función (1/alfa) * cos (pi/alfa), que oscila suavemente hasta el intervalo [-.2, .2], donde oscila rápidamente, yendo al infinito y al infinito negativo a medida que se acerca al eje y.](https://math.libretexts.org/@api/deki/files/1863/CNX_Calc_Figure_02_02_214.jpeg)
En los ejercicios 17 - 20, considere la gráfica de la función que\(y=f(x)\) se muestra aquí. ¿Cuáles de las afirmaciones sobre\(y=f(x)\) son verdaderas y cuáles son falsas? Explique por qué una declaración es falsa.
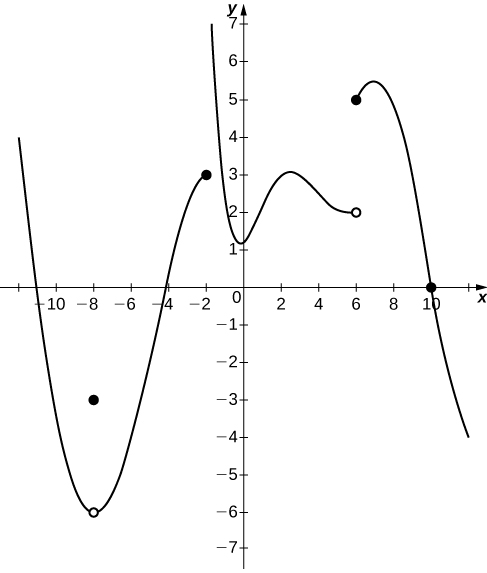
17)\(\displaystyle \lim_{x→10}f(x)=0\)
18)\(\displaystyle \lim_{x→−2^+}f(x)=3\)
- Responder
- Falso;\(\displaystyle \lim_{x→−2^+}f(x)=+∞\)
19)\(\displaystyle \lim_{x→−8}f(x)=f(−8)\)
20)\(\displaystyle \lim_{x→6}f(x)=5\)
- Responder
- Falso;\(\displaystyle \lim_{x→6}f(x)\) DNE desde\(\displaystyle \lim_{x→6^−}f(x)=2\) y\(\displaystyle \lim_{x→6^+}f(x)=5\).
En los ejercicios 21 - 25, utilice la siguiente gráfica de la función\(y=f(x)\) para encontrar los valores, si es posible. Estimar cuando sea necesario.
1. El primer segmento es lineal con una pendiente de 1 y pasa por el origen. Su punto final es un círculo cerrado en (1,1). El segundo segmento también es lineal con una pendiente de -1. Comienza con el círculo abierto en (1,2)." style="width: 417px; height: 424px;" width="417px" height="424px" src="https://math.libretexts.org/@api/dek...02_02_202.jpeg">
21)\(\displaystyle \lim_{x→1^−}f(x)\)
22)\(\displaystyle \lim_{x→1^+}f(x)\)
- Responder
- \(2\)
23)\(\displaystyle \lim_{x→1}f(x)\)
24)\(\displaystyle \lim_{x→2}f(x)\)
- Responder
- \(1\)
25)\(f(1)\)
En los ejercicios 26 - 29, utilice la gráfica de la función que\(y=f(x)\) se muestra aquí para encontrar los valores, si es posible. Estimar cuando sea necesario.
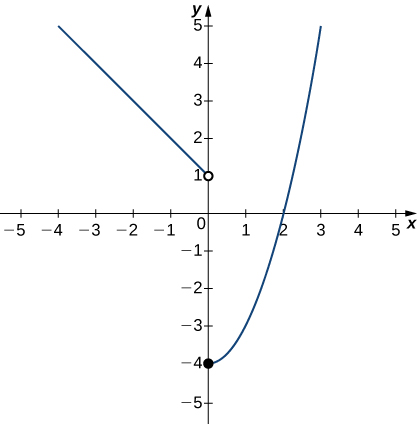
26)\(\displaystyle \lim_{x→0^−}f(x)\)
- Responder
- \(1\)
27)\(\displaystyle \lim_{x→0^+}f(x)\)
28)\(\displaystyle \lim_{x→0}f(x)\)
- Responder
- DNE
29)\(\displaystyle \lim_{x→2}f(x)\)
En los ejercicios 30 - 35, utilice la gráfica de la función que\(y=f(x)\) se muestra aquí para encontrar los valores, si es posible. Estimar cuando sea necesario.
2, tiene una pendiente de 1, y comienza en el círculo abierto (2,2)." style="width: 417px; height: 424px;" width="417px" height="424px" src="https://math.libretexts.org/@api/dek...02_02_204.jpeg">
30)\(\displaystyle \lim_{x→−2^−}f(x)\)
- Responder
- \(0\)
31)\(\displaystyle \lim_{x→−2^+}f(x)\)
32)\(\displaystyle \lim_{x→−2}f(x)\)
- Responder
- DNE
33)\(\displaystyle \lim_{x→2^−}f(x)\)
34)\(\displaystyle \lim_{x→2^+}f(x)\)
- Responder
- \(2\)
35)\(\displaystyle \lim_{x→2}f(x)\)
En los ejercicios 36 - 38, usa la gráfica de la función que\(y=g(x)\) se muestra aquí para encontrar los valores, si es posible. Estimar cuando sea necesario.
=0 y es la mitad izquierda de una parábola de apertura hacia arriba con vértice en el círculo cerrado (0,3). El segundo existe para x>0 y es la mitad derecha de una parábola de apertura hacia abajo con vértice en el círculo abierto (0,0)." style="width: 417px; height: 424px;" width="417px" height="424px" src="https://math.libretexts.org/@api/dek...02_02_205.jpeg">
36)\(\displaystyle \lim_{x→0^−}g(x)\)
- Responder
- \(3\)
37)\(\displaystyle \lim_{x→0^+}g(x)\)
38)\(\displaystyle \lim_{x→0}g(x)\)
- Responder
- DNE
En los ejercicios 39 - 41, utilice la gráfica de la función que\(y=h(x)\) se muestra aquí para encontrar los valores, si es posible. Estimar cuando sea necesario.
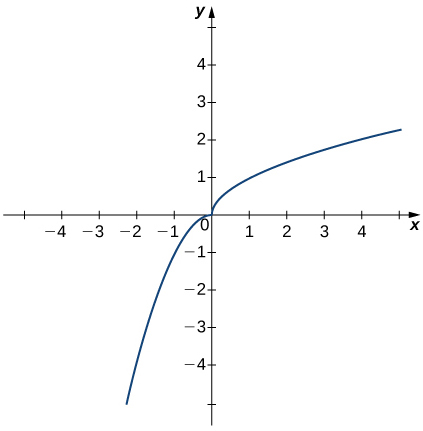
39)\(\displaystyle \lim_{x→0^−}h(x)\)
40)\(\displaystyle \lim_{x→0^+}h(x)\)
- Responder
- \(0\)
41)\(\displaystyle \lim_{x→0}h(x)\)
En los ejercicios 42 - 46, utilice la gráfica de la función que\(y=f(x)\) se muestra aquí para encontrar los valores, si es posible. Estimar cuando sea necesario.
0, y hay un círculo cerrado en el origen." style="width: 417px; height: 424px;" width="417px" height="424px" src="https://math.libretexts.org/@api/dek...02_02_207.jpeg">
42)\(\displaystyle \lim_{x→0^−}f(x)\)
- Responder
- \(-2\)
43)\(\displaystyle \lim_{x→0^+}f(x)\)
44)\(\displaystyle \lim_{x→0}f(x)\)
- Responder
- DNE
45)\(\displaystyle \lim_{x→1}f(x)\)
46)\(\displaystyle \lim_{x→2}f(x)\)
- Responder
- \(0\)
Límites Infinitos
En los ejercicios 47 - 51, bosquejar la gráfica de una función con las propiedades dadas.
47) no\(\displaystyle \lim_{x→2}f(x)=1, \quad \lim_{x→4^−}f(x)=3, \quad \lim_{x→4^+}f(x)=6, \quad x=4\) está definido.
48)\(\displaystyle \lim_{x→−∞}f(x)=0, \quad \lim_{x→−1^−}f(x)=−∞, \quad \lim_{x→−1^+}f(x)=∞,\quad \lim_{x→0}f(x)=f(0), \quad f(0)=1, \quad \lim_{x→∞}f(x)=−∞\)
- Responder
-
Las respuestas pueden variar
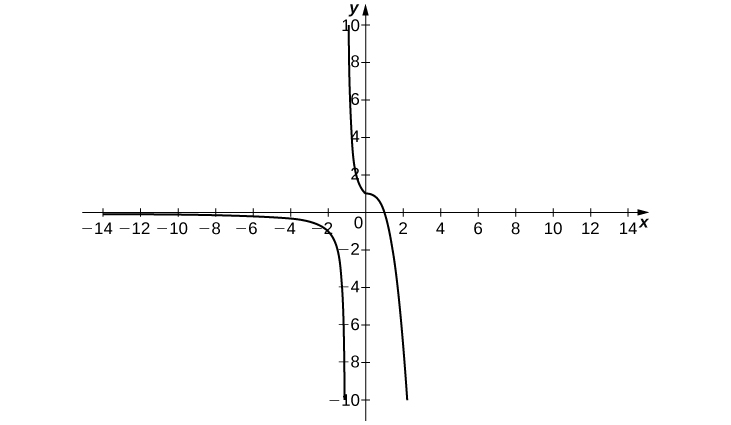
49)\(\displaystyle \lim_{x→−∞}f(x)=2, \quad \lim_{x→3^−}f(x)=−∞, \quad \lim_{x→3^+}f(x)=∞, \quad \lim_{x→∞}f(x)=2, \quad f(0)=-\frac{1}{3}\)
50)\(\displaystyle \lim_{x→−∞}f(x)=2,\quad \lim_{x→−2}f(x)=−∞,\quad \lim_{x→∞}f(x)=2,\quad f(0)=0\)
- Responder
-
La respuesta puede variar
51)\(\displaystyle \lim_{x→−∞}f(x)=0,\quad \lim_{x→−1^−}f(x)=∞,\quad \lim_{x→−1^+}f(x)=−∞, \quad f(0)=−1, \quad \lim_{x→1^−}f(x)=−∞, \quad \lim_{x→1^+}f(x)=∞, \quad \lim_{x→∞}f(x)=0\)
52) Las ondas de choque surgen en muchas aplicaciones físicas, que van desde supernovas hasta ondas de detonación. Aquí se muestra una gráfica de la densidad de una onda de choque con respecto a la distancia\(x\),,. Nos interesa principalmente la ubicación del frente del choque, etiquetado\(X_{SF}\) en el diagrama.
p2 y xsf en el eje x. Consiste en y= p1 de 0 a xsf, x = xsf de y= p1 a y=p2, e y=p2 para valores mayores o iguales a xsf." style="width: 300px; height: 304px;" width="300px" height="304px" src="https://math.libretexts.org/@api/dek...avedensity.png">
a. Evaluar\(\displaystyle \lim_{x→X_{SF}^+}ρ(x)\).
b. Evaluar\(\displaystyle \lim_{x→X_{SF}^−}ρ(x)\).
c. Evaluar\(\displaystyle \lim_{x→X_{SF}}ρ(x)\). Explica los significados físicos detrás de tus respuestas.
- Responder
- a.\(ρ_2\) b.\(ρ_1\) c. DNE a menos que\(ρ_1=ρ_2\). A medida que te acercas\(X_{SF}\) desde la derecha, estás en el área de alta densidad del choque. Cuando te acercas desde la izquierda, aún no has experimentado el “choque” y estás en una densidad menor.
53) Un entrenador de pista utiliza una cámara con obturador rápido para estimar la posición de un corredor con respecto al tiempo. Aquí se da una tabla de los valores de posición del atleta versus tiempo, donde\(x\) está la posición en metros del corredor y\(t\) es tiempo en segundos. ¿Qué es\(\displaystyle \lim_{t→2}x(t)\)? ¿Qué significa físicamente?
| \(t(sec)\) | \(x(m)\) |
|---|---|
| \ (t (seg)\)” style="text-align:center; ">1.75 | \ (x (m)\)” style="text-align:center; ">4.5 |
| \ (t (seg)\)” style="text-align:center; ">1.95 | \ (x (m)\)” style="text-align:center; ">6.1 |
| \ (t (seg)\)” style="text-align:center; ">1.99 | \ (x (m)\)” style="text-align:center; ">6.42 |
| \ (t (seg)\)” style="text-align:center; ">2.01 | \ (x (m)\)” style="text-align:center; ">6.58 |
| \ (t (seg)\)” style="text-align:center; ">2.05 | \ (x (m)\)” style="text-align:center; ">6.9 |
| \ (t (seg)\)” style="text-align:center; ">2.25 | \ (x (m)\)” style="text-align:center; ">8.5 |