3.5E: Ejercicios para la Sección 3.5

Última actualización
Guardar como PDF

Page ID: 116616

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En los ejercicios 1 - 10, encuentra$\dfrac{dy}{dx}$ para las funciones dadas.

1)$y=x^2−\sec x+1$

Contestar: $\dfrac{dy}{dx}=2x−\sec x\tan x$

2)$y=3\csc x+\dfrac{5}{x}$

3)$y=x^2\cot x$

Contestar: $\dfrac{dy}{dx}=2x\cot x−x^2\csc^2 x$

4)$y=x−x^3\sin x$

5)$y=\dfrac{\sec x}{x}$

Contestar: $\dfrac{dy}{dx}=\dfrac{x\sec x\tan x−\sec x}{x^2}$

6)$y=\sin x\tan x$

7)$y=(x+\cos x)(1−\sin x)$

Contestar: $\dfrac{dy}{dx}=(1−\sin x)(1−\sin x)−\cos x(x+\cos x)$

8)$y=\dfrac{\tan x}{1−\sec x}$

9)$y=\dfrac{1−\cot x}{1+\cot x}$

Contestar: $\dfrac{dy}{dx}=\dfrac{2\csc^2 x}{(1+\cot x)^2}$

10)$y=(\cos x)(1+\csc x)$

En los ejercicios 11 - 16, encuentra la ecuación de la línea tangente a cada una de las funciones dadas en los valores indicados de$x$. Luego usa una calculadora para graficar tanto la función como la línea tangente para asegurar que la ecuación para la línea tangente sea correcta.

11) [T]$f(x)=−\sin x,\quad x=0$

Contestar

$y=−x$

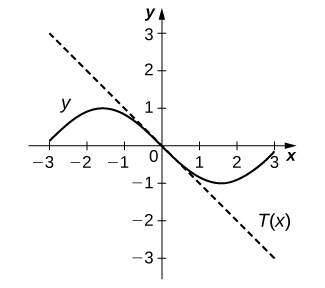
$La gráfica muestra el pecado negativo (x) y la línea recta T (x) con pendiente −1 e intercepción y 0.$

12) [T]$f(x)=\csc x,\quad x=\frac{π}{2}$

13) [T]$f(x)=1+\cos x,\quad x=\frac{3π}{2}$

Contestar

$y=x+\frac{2−3π}{2}$

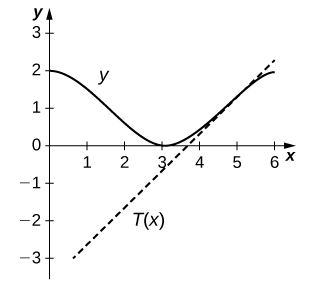
$El gráfico muestra la función coseno desplazada hacia arriba uno y tiene la línea recta T (x) con pendiente 1 e intercepción y (2 — 3π) /2.$

14) [T]$f(x)=\sec x,\quad x=\frac{π}{4}$

15) [T]$f(x)=x^2−\tan x, \quad x=0$

Contestar

$y=−x$

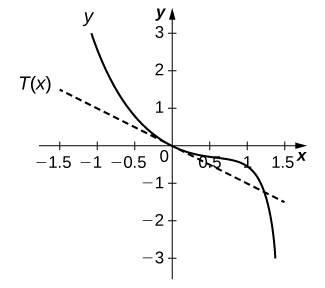
$El gráfico muestra la función como comenzando en (−1, 3), disminuyendo al origen, continuando disminuyendo lentamente hasta aproximadamente (1, −0.5), punto en el que disminuye muy rápidamente.$

16) [T]$f(x)=5\cot x, \quad x=\frac{π}{4}$

En los ejercicios 17 - 22, encuentra$\dfrac{d^2y}{dx^2}$ para las funciones dadas.

17)$y=x\sin x−\cos x$

Contestar: $\dfrac{d^2y}{dx^2} = 3\cos x−x\sin x$

18)$y=\sin x\cos x$

19)$y=x−\frac{1}{2}\sin x$

Contestar: $\dfrac{d^2y}{dx^2} = \frac{1}{2}\sin x$

20)$y=\dfrac{1}{x}+\tan x$

21)$y=2\csc x$

Contestar: $\dfrac{d^2y}{dx^2} = 2\csc(x)\left(\csc^2(x)+\cot^2(x)\right) $

22)$y=\sec^2 x$

23) Encuentra todos$x$ los valores en la gráfica de$f(x)=−3\sin x\cos x$ donde la línea tangente es horizontal.

Contestar: $x = \dfrac{(2n+1)π}{4}$, donde$n$ es un número entero

24) Encuentra todos$x$ los valores en la gráfica de$f(x)=x−2\cos x$ para$0<x<2π$ donde la línea tangente tiene pendiente 2.

25) Dejar$f(x)=\cot x.$ Determinar los puntos en la gráfica de$f$ para$0<x<2π$ donde la (s) línea (s) tangente (s) es (son) paralela a la línea$y=−2x$.

Contestar: $\left(\frac{π}{4},1\right),\quad \left(\frac{3π}{4},−1\right),\quad\left(\frac{5π}{4},1\right),\quad \left(\frac{7π}{4},−1\right)$

26) [T] Una masa en un resorte rebota hacia arriba y hacia abajo en simple movimiento armónico, modelada por la función$s(t)=−6\cos t$ donde s se mide en pulgadas y$t$ se mide en segundos. Encuentre la velocidad a la que el resorte oscila en$t=5$ s.

27) Dejar que la posición de un péndulo oscilante en simple movimiento armónico sea dada por$s(t)=a\cos t+b\sin t$. Encuentra las constantes$a$ y$b$ tal que cuando la velocidad es de 3 cm/s,$s=0$ y$t=0$.

Contestar: $a=0,\quad b=3$

28) Después de que un buceador salta de una tabla de buceo, el borde de la tabla oscila con la posición dada por$s(t)=−5\cos t$ cm a$t$ segundos después del salto.

a. Esbozar un periodo de la función de posición para$t≥0$.

b. Encuentra la función de velocidad.

c. Esbozar un periodo de la función de velocidad para$t≥0$.

d. Determinar los tiempos en que la velocidad es$0$ superior a un periodo.

e. Encuentra la función de aceleración.

f. Esbozar un periodo de la función de aceleración para$t≥0$.

29) El número de hamburguesas vendidas en un restaurante de comida rápida en Pasadena, California, viene dado por$y=10+5\sin x$ dónde$y$ está el número de hamburguesas vendidas y$x$ representa el número de horas después de que el restaurante abrió a las 11 de la mañana hasta las 11 de la noche, cuando cierra la tienda. Encuentra$y'$ y determina los intervalos donde va en aumento el número de hamburguesas que se venden.

Contestar: $y′=5\cos(x)$, aumentando en$\left(0,\frac{π}{2}\right),\;\left(\frac{3π}{2},\frac{5π}{2}\right)$, y$\left(\frac{7π}{2},12\right)$

30) [T] La cantidad de lluvias mensuales en Phoenix, Arizona, puede aproximarse por$y(t)=0.5+0.3\cos t$, donde$t$ es meses desde enero. Encuentre$y′$ y use una calculadora para determinar los intervalos donde la cantidad de lluvia que cae está disminuyendo.

Para los ejercicios 31 - 33, use la regla del cociente para derivar las ecuaciones dadas.

31)$\dfrac{d}{dx}(\cot x)=−\csc^2x$

32)$\dfrac{d}{dx}(\sec x)=\sec x\tan x$

33)$\dfrac{d}{dx}(\csc x)=−\csc x\cot x$

34) Utilizar la definición de derivado y la identidad$\cos(x+h)=\cos x\cos h−\sin x\sin h$ para demostrarlo$\dfrac{d}{dx}(\cos x)=−\sin x$.

Para los ejercicios 35 - 39, encuentre la derivada de orden superior solicitada para las funciones dadas.

35)$\dfrac{d^3y}{dx^3}$ de$y=3\cos x$

Contestar: $\dfrac{d^3y}{dx^3} = 3\sin x$

36)$\dfrac{d^2y}{dx^2}$ de$y=3\sin x+x^2\cos x$

37)$\dfrac{d^4y}{dx^4}$ de$y=5\cos x$

Contestar: $\dfrac{d^4y}{dx^4} = 5\cos x$

38)$\dfrac{d^2y}{dx^2}$ de$y=\sec x+\cot x$

39)$\dfrac{d^3y}{dx^3}$ de$y=x^{10}−\sec x$

Contestar: $\dfrac{d^3y}{dx^3} = 720x^7−5\tan(x)\sec^3(x)−\tan^3(x)\sec(x)$