3.7E: Ejercicios para la Sección 3.7

Última actualización
Guardar como PDF

Page ID: 116606

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En los ejercicios 1 - 4, utilice la gráfica de$y=f(x)$ a

a. esbozar la gráfica de$y=f^{−1}(x)$, y

b. utilizar la parte a. para estimar$\big(f^{−1}\big)′(1)$.

$Una línea recta que pasa por (0, −3) y (3, 3).$

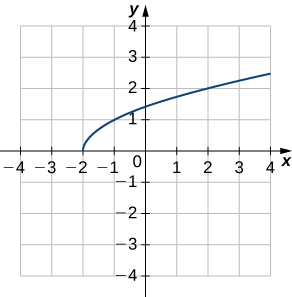
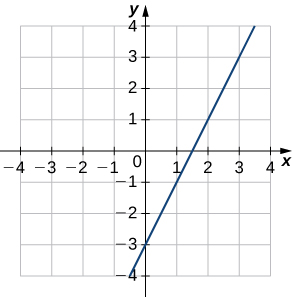
$Una línea curva que comienza en (−2, 0) y que pasa por (−1, 1) y (2, 2).$

Contestar

$alt$

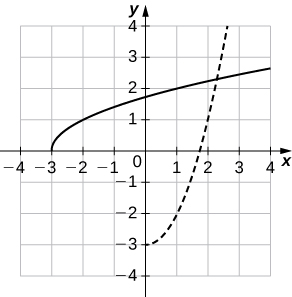
b.$(f^{−1})′(1)\approx 2$

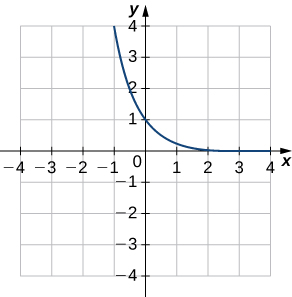
$Una línea curva que comienza en (4, 0) y que pasa por (0, 1) y (−1, 4).$

$Un cuarto de círculo que comienza en (0, 4) y termina en (4, 0).$

Responder

$Un cuarto de círculo que comienza en (0, 4) y termina en (4, 0).$

b.$(f^{−1})′(1)\approx −1/\sqrt{3}$

Para los ejercicios 5 - 8, use la función dada$y=f(x)$ para encontrar

a.$\dfrac{df}{dx}$ en$x=a$ y

b$x=f^{−1}(y)$.

c. Luego use la parte b. para encontrar$\dfrac{df^{−1}}{dy}$ en$y=f(a).$

5)$f(x)=6x−1,\; x=−2$

6)$f(x)=2x^3−3,\; x=1$

Responder: a.$\dfrac{df}{dx} = 6$
b.$x=f^{−1}(y)=\left(\dfrac{y+3}{2}\right)^{1/3}$
c.$\dfrac{df^{−1}}{dy} = \frac{1}{6}$

7)$f(x)=9−x^2,\; 0≤x≤3,x=2$

8)$f(x)=\sin x,\; x=0$

Responder: a.$\dfrac{df}{dx} = 1$
b.$x=f^{−1}(y)=\sin^{−1}y$
c.$\dfrac{df^{−1}}{dy} = 1$

Para cada función en los ejercicios 9 - 14, encuentra$\big(f^{−1}\big)′(a)$.

9)$f(x)=x^2+3x+2,\; x≥−1,\; a=2$

10$f(x)=x^3+2x+3,\; a=0$

Responder: $\big(f^{−1}\big)′(1) = \frac{1}{5}$

11)$f(x)=x+\sqrt{x},\; a=2$

12)$f(x)=x−\frac{2}{x},\; x<0,\; a=1$

Responder: $\big(f^{−1}\big)′(1) = \frac{1}{3}$

13)$f(x)=x+\sin x,\; a=0$

14)$f(x)=\tan x+3x^2,\; a=0$

Responder: $\big(f^{−1}\big)′(0) = 1$

Para cada función$y=f(x)$, impartida en los ejercicios 15 a 19,

a. encontrar la pendiente de la línea tangente a su función inversa$f^{−1}$ en el punto indicado$P$, y

b. encontrar la ecuación de la línea tangente a la gráfica de$f^{−1}$ en el punto indicado.

15)$f(x)=\dfrac{4}{1+x^2},\quad P(2,1)$

16)$f(x)=\sqrt{x−4},\quad P(2,8)$

Responder: a.$4$
b.$y=4x$

17)$f(x)=(x^3+1)^4,\quad P(16,1)$

18)$f(x)=−x^3−x+2,\quad P(−8,2)$

Responder: a.$−\frac{1}{96}$
b.$y=−\frac{1}{13}x+\frac{18}{13}$

19)$f(x)=x^5+3x^3−4x−8,\quad P(−8,1)$

En los ejercicios 20 - 29, encuentra$\dfrac{dy}{dx}$ para la función dada.

20)$y=\sin^{−1}(x^2)$

Responder: $\dfrac{dy}{dx} = \dfrac{2x}{\sqrt{1−x^4}}$

21)$y=\cos^{−1}\left(\sqrt{x}\right)$

22)$y=\sec^{−1}\left(\frac{1}{x}\right)$

Responder: $\dfrac{dy}{dx} = \dfrac{−1}{\sqrt{1−x^2}}$

23)$y=\sqrt{\csc^{−1}x}$

24)$y=(1+\tan^{−1}x)^3$

Responder: $\dfrac{dy}{dx} = \dfrac{3(1+\tan^{−1}x)^2}{1+x^2}$

25)$y=\cos^{−1}(2x)⋅\sin^{−1}(2x)$

26)$y=\dfrac{1}{\tan^{−1}(x)}$

Responder: $\dfrac{dy}{dx} = \dfrac{−1}{(1+x^2)(\tan^{−1}x)^2}$

27)$y=\sec^{−1}(−x)$

28)$y=\cot^{−1}\sqrt{4−x^2}$

Responder: $\dfrac{dy}{dx} = \dfrac{x}{(5−x^2)\sqrt{4−x^2}}$

29)$y=x⋅\csc^{−1}x$

En los ejercicios 30 - 35, usa los valores dados para encontrar$\big(f^{−1}\big)′(a)$.

30)$f(π)=0,f'(π)=−1,a=0$

Responder: $\big(f^{−1}\big)′(0) = −1$

31)$f(6)=2,\; f′(6)=\frac{1}{3},\; a=2$

32)$f(\frac{1}{3})=−8,\; f'(\frac{1}{3})=2,\; a=−8$

Responder: $\big(f^{−1}\big)′(-8) = \frac{1}{2}$

33)$f(\sqrt{3})=\frac{1}{2},f'(\sqrt{3})=\frac{2}{3},a=\frac{1}{2}$

34)$f(1)=−3,\; f'(1)=10,\; a=−3$

Responder: $\big(f^{−1}\big)′(-3) =\frac{1}{10}$

35)$f(1)=0,\; f'(1)=−2,\; a=0$

36) [T] La posición de un disco de hockey en movimiento después de$t$ segundos es$s(t)=tan^{−1}t$ donde$s$ está en metros.

a. Encuentra la velocidad del disco de hockey en cualquier momento$t$.

b. Encuentra la aceleración del disco en cualquier momento$t$.

c. Evaluar las partes a. y b. por$t=2,\, 4$, y$6$ segundos.

d. ¿Qué conclusión puede extraerse de los resultados en c.?

Responder

a.$v(t)=\dfrac{1}{1+t^2}$
b.$a(t)=\dfrac{−2t}{(1+t^2)^2}$
c. a)$0.2,\, 0.06,\, 0.03$; b)$−0.16,\, −0.028,\, −0.0088$

d. El disco de hockey se desacelera/desacelera a los 2, 4 y 6 segundos.

Solución:

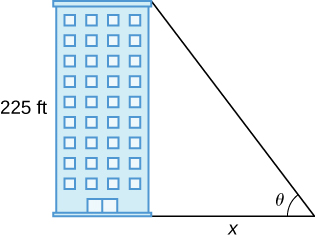
37) [T] Un edificio que mide 225 pies de altura proyecta una sombra de varias longitudes a$x$ medida que pasa el día. Un ángulo de elevación$θ$ está formado por líneas desde la parte superior e inferior del edificio hasta la punta de la sombra, como se ve en la siguiente figura. Encuentra la tasa de cambio del ángulo de elevación$\frac{dθ}{dx}$ cuando$x=272$ los pies.

$Se muestra un edificio con una altura de 225 pies. Se hace un triángulo con la altura del edificio como el lado opuesto al ángulo θ. El lado adyacente tiene longitud x.$

38) [T] Un poste mide 75 pies de altura. $θ$Se forma un ángulo cuando se unen cables de varias longitudes de$x$ pies desde el suelo hasta la parte superior del poste, como se muestra en la siguiente figura. Encuentre la tasa de cambio del ángulo$\frac{dθ}{dx}$ cuando se fija un cable de 90 pies de longitud.

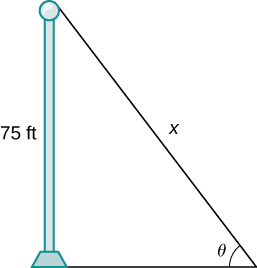
$Se muestra un asta de bandera con una altura de 75 pies. Se hace un triángulo con la altura del asta de bandera como el lado opuesto al ángulo θ. La hipotenusa tiene longitud x.$

Responder: $−0.0168$radianes por pie

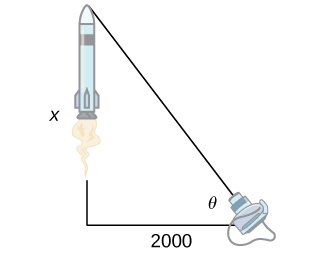
39) [T] Una cámara de televisión a nivel del suelo se encuentra a 2000 pies de distancia de la plataforma de lanzamiento de un cohete espacial que está configurado para despegar verticalmente, como se ve en la siguiente figura. El ángulo de elevación de la cámara se puede encontrar por$θ=\tan^{−1}\left(\frac{x}{2000}\right)$, donde$x$ está la altura del cohete. Encuentra la tasa de cambio del ángulo de elevación después del lanzamiento cuando la cámara y el cohete están a 5000 pies de distancia.

$Se muestra un cohete con en el aire con la distancia desde su morro hasta el suelo siendo x Se hace un triángulo con la altura del cohete como lado opuesto al ángulo θ. El lado adyacente tiene una longitud 2000.$

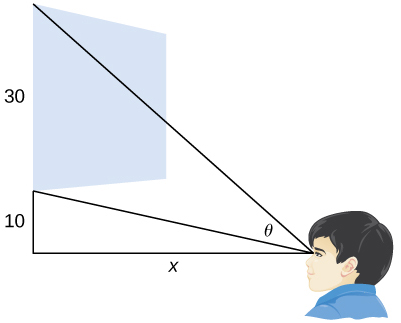
40) [T] Una sala de cine local con una pantalla de 30 pies de altura que está a 10 pies por encima del nivel de los ojos de una persona cuando está sentada tiene un ángulo de visión$θ$ (en radianes) dado por$θ=\cot^{−1}\frac{x}{40}−\cot^{−1}\frac{x}{10}$,

donde$x$ está la distancia en pies de distancia de la pantalla de cine a la que está sentada la persona, como se muestra en la siguiente figura.

$A una persona se le muestra con un triángulo rectángulo que viene de su ojo (el ángulo recto está en el lado opuesto al ojo), con altura 10 y base x Hay una línea trazada desde el ojo hasta la parte superior de la pantalla, que forma un ángulo θ con la hipotenusa del triángulo. La pantalla tiene una altura de 30.$

a. Encontrar$\dfrac{dθ}{dx}$.

b. Evaluar$\dfrac{dθ}{dx}$ para$x=5,\,10,\,15,$ y$20$.

c. Interpretar los resultados de la parte b.

d. Evaluar$\dfrac{dθ}{dx}$ para$x=25,\,30,\,35$, y$40$.

e. Interpretar los resultados en la parte d. ¿A qué distancia$x$ debe pararse la persona para maximizar su ángulo de visión?

Responder: a.$\dfrac{dθ}{dx}=\dfrac{10}{100+x^2}−\dfrac{40}{1600+x^2}$
b.$\frac{18}{325},\,\frac{9}{340},\,\frac{42}{4745},\,0$
c. A medida que una persona se aleja más de la pantalla, el ángulo de visión va aumentando, lo que implica que a medida que se aleja más, su visión en pantalla se va ensanchando. d.$−\frac{54}{12905},\,−\frac{3}{500},\,−\frac{198}{29945},\,−\frac{9}{1360}$
e. A medida que la persona se mueve más allá de los 20 pies desde la pantalla, el ángulo de visión está disminuyendo. La distancia óptima que debe soportar la persona para maximizar el ángulo de visión es de 20 pies.