3.8E: Ejercicios para la Sección 3.8

Última actualización
Guardar como PDF

Page ID: 116664

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

En los ejercicios 1 - 10, utilizar la diferenciación implícita para encontrar$\dfrac{dy}{dx}$.

1)$x^2−y^2=4$

2)$6x^2+3y^2=12$

Contestar: $\dfrac{dy}{dx}=\dfrac{−2x}{y}$

3)$x^2y=y−7$

4)$3x^3+9xy^2=5x^3$

Contestar: $\dfrac{dy}{dx}=\dfrac{x}{3y}−\dfrac{y}{2x}$

5)$xy−\cos(xy)=1$

6)$y\sqrt{x+4}=xy+8$

Contestar: $\dfrac{dy}{dx}=\dfrac{y−\dfrac{y}{2\sqrt{x+4}}}{\sqrt{x+4}−x}$

7)$−xy−2=\frac{x}{7}$

8)$y\sin(xy)=y^2+2$

Contestar: $\dfrac{dy}{dx}=\dfrac{y^2\cos(xy)}{2y−\sin(xy)−xy\cos(xy)}$

9)$(xy)^2+3x=y^2$

10)$x^3y+xy^3=−8$

Contestar: $\dfrac{dy}{dx}=\dfrac{−3x^2y−y^3}{x^3+3xy^2}$

Para los ejercicios 11 - 16, encuentra la ecuación de la línea tangente a la gráfica de la ecuación dada en el punto indicado. Use una calculadora o software de computadora para graficar la función y la línea tangente.

11) [T]$x^4y−xy^3=−2, \quad (−1,−1)$

12) [T]$x^2y^2+5xy=14,\quad (2,1)$

Contestar

$y=−\frac{1}{2}x+2$

$La gráfica tiene una media luna en cada uno de los cuatro cuadrantes. Hay una línea recta marcada con T (x) con pendiente −1/2 e intersección y 2.$

13) [T]$\tan(xy)=y,\quad \left(\frac{π}{4},1\right)$

14) [T]$xy^2+\sin(πy)−2x^2=10, \quad (2,−3)$

Contestar

$y=\frac{1}{π+12}x−\frac{3π+38}{π+12}$

$La gráfica tiene dos curvas, una en el primer cuadrante y otra en el cuarto cuadrante. Son simétricos alrededor del eje x. La curva en el primer cuadrante va de (0.3, 5) a (1.5, 3.5) a (5, 4). Hay una línea recta marcada T (x) con pendiente 1/ (π + 12) e y intercept − (3π + 38)/(π + 12).$

15) [T]$\dfrac{x}{y}+5x−7=−\frac{3}{4}y, \quad (1,2)$

16) [T]$xy+\sin(x)=1,\quad \left(\frac{π}{2},0\right)$

Contestar

$y=0$

$La gráfica comienza en el tercer cuadrante cerca (−5, 0), permanece cerca de 0 hasta x = −4, punto en el que disminuye hasta llegar cerca (0, −5). Hay una asíntota en x = 0. La gráfica comienza de nuevo cerca (0, 5) disminuye a (1, 0) y luego aumenta un poco antes de disminuir para estar cerca (5, 0). Hay una línea recta marcada con T (x) que coincide con y = 0.$

17) [T] La gráfica de un folium de Descartes con ecuación$2x^3+2y^3−9xy=0$ se da en la siguiente gráfica.

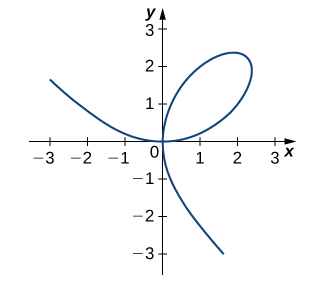
$Se grafica un folium que tiene la ecuación 2x3 + 2y3 — 9xy = 0. Se cruza sobre sí mismo en (0, 0).$

a. Encuentra la ecuación de la línea tangente en el punto$(2,1)$. Grafica la línea tangente junto con el folium.

b. Encuentra la ecuación de la línea normal a la línea tangente en a. en el punto$(2,1)$.

18) Para la ecuación$x^2+2xy−3y^2=0,$

a. Encuentra la ecuación de la línea normal a la tangente en el punto$(1,1)$.

b. ¿En qué otro punto la línea normal en a. interseca la gráfica de la ecuación?

Contestar: a.$y=−x+2$
b.$(3,−1)$

19) Encuentra todos los puntos de la gráfica$y^3−27y=x^2−90$ en los que la línea tangente es vertical.

20) Para la ecuación$x^2+xy+y^2=7$,

a. Encuentra la (s)$x$ intercepción (s).

b.Encuentra la pendiente de la (s) línea (s) tangente (s) en la (s)$x$ intersección (s).

c. ¿Qué indica el (los) valor (s) de la parte b. sobre la (s) línea (s) tangente (s)?

Contestar: a.$\left(±\sqrt{7},0\right)$
b.$−2$
c. Son paralelas ya que la pendiente es la misma en ambas intercepciones.

21) Encuentra la ecuación de la línea tangente a la gráfica de la ecuación$\sin^{−1}x+\sin^{−1}y=\frac{π}{6}$ en el punto$\left(0,\frac{1}{2}\right)$.

22) Encuentra la ecuación de la línea tangente a la gráfica de la ecuación$\tan^{−1}(x+y)=x^2+\frac{π}{4}$ en el punto$(0,1)$.

Contestar: $y=−x+1$

23) Encontrar$y′$ y$y''$ para$x^2+6xy−2y^2=3$.

24) [T] El número de celulares producidos cuando los$x$ dólares se gastan en mano de obra y los$y$ dólares se gastan en capital invertido por un fabricante pueden modelarse mediante la ecuación$60x^{3/4}y^{1/4}=3240$.

a. Encontrar$\frac{dy}{dx}$ y evaluar en el punto$(81,16)$.

b. Interpretar el resultado de a.

Contestar: a.$\frac{dy}{dx}=−0.5926$
b. Cuando se gastan 81 dólares en mano de obra y 16 dólares se gastan en capital, la cantidad gastada en capital disminuye en $0.5926 por cada dólar gastado en mano de obra.

25) [T] El número de automóviles producidos cuando los$x$ dólares se gastan en mano de obra y los$y$ dólares se gastan en capital invertido por un fabricante pueden modelarse mediante la ecuación$30x^{1/3}y^{2/3}=360$.

(Ambos$x$ y$y$ se miden en miles de dólares.)

a. Encontrar$\frac{dy}{dx}$ y evaluar en el punto$(27,8)$.

b. Interpretar el resultado de la parte a.

26) El volumen de un cono circular derecho de radio$x$ y altura$y$ viene dado por$V=\frac{1}{3}πx^2y$. Supongamos que el volumen del cono es$85π\,\text{cm}^3$. Encuentra$\dfrac{dy}{dx}$ cuándo$x=4$ y$y=16$.

Contestar: $\dfrac{dy}{dx} = −8$

Para los ejercicios 27 - 28, considere una caja rectangular cerrada con una base cuadrada con lado$x$ y altura$y$.

27) Encontrar una ecuación para el área de superficie de la caja rectangular,$S(x,y)$.

28) Si el área de superficie de la caja rectangular es de 78 pies cuadrados, encuentre$\dfrac{dy}{dx}$ cuando$x=3$ pies y$y=5$ pies.

Contestar: $\dfrac{dy}{dx} = −2.67$

En los ejercicios 29 - 31, utilizar la diferenciación implícita para determinar$y′$. ¿La respuesta concuerda con las fórmulas que hemos determinado previamente?

29)$x=\sin y$

30)$x=\cos y$

Contestar: $y′=−\dfrac{1}{\sqrt{1−x^2}}$

31)$x=\tan y$

Search

Text Color

Text Size

Margin Size

Font Type