4.1E: Ejercicios para la Sección 4.1

Última actualización
Guardar como PDF

Page ID: 116454

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En los ejercicios 1 - 3, encuentra las cantidades para la ecuación dada.

1) Encuentra$\frac{dy}{dt}$ en$x=1$ y$y=x^2+3$ si$\frac{dx}{dt}=4.$

Contestar: $\dfrac{dy}{dt} = 8$

2) Encuentra$\frac{dx}{dt}$ en$x=−2$ y$y=2x^2+1$ si$\frac{dy}{dt}=−1.$

3) Encontrar$\frac{dz}{dt}$ en$(x,y)=(1,3)$ y$z^2=x^2+y^2$ si$\frac{dx}{dt}=4$ y$\frac{dy}{dt}=3$.

Contestar: $\dfrac{dz}{dt} = \frac{13}{\sqrt{10}}$

En los ejercicios 4 - 15, bosquejar la situación si es necesario y utilizó tarifas relacionadas para resolver por las cantidades.

4) [T] Si dos resistencias eléctricas están conectadas en paralelo, la resistencia total (medida en ohmios, denotada por la letra griega mayúscula omega,$Ω$) viene dada por la ecuación$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}.$ Si$R_1$ está aumentando a una velocidad de$0.5Ω/\text{min}$ y$R_2$ disminuye a una velocidad de$1.1Ω/\text{min}$, a qué velocidad ¿cambia la resistencia total cuando$R_1=20Ω$ y$R_2=50Ω/\text{min}$?

5) Una escalera$10$ de pies está apoyada contra una pared. Si la parte superior de la escalera se desliza por la pared a una velocidad de$2$ pies/seg, ¿qué tan rápido se mueve la parte inferior a lo largo del suelo cuando la parte inferior de la escalera está a$5$ pies de la pared?

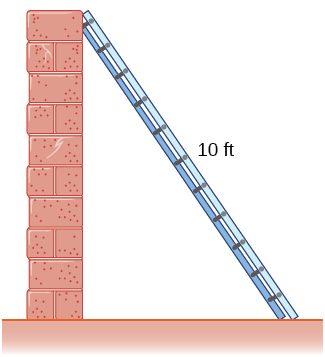
$Un triángulo rectángulo está formado por una escalera apoyada contra una pared de ladrillo. La escalera forma la hipotenusa y mide 10 pies de largo.$

Contestar: $2\sqrt{3}$pies/seg

6) Una escalera$25$ de pies está apoyada contra una pared. Si empujamos la escalera hacia la pared a una velocidad de$1$ pies/seg, y la parte inferior de la escalera está inicialmente a$20$ pies de distancia de la pared, ¿qué tan rápido se mueve la escalera hacia arriba por la pared$5$ segundos después de que comenzamos a empujar?

7) Dos aviones están volando en el aire a la misma altura: el avión A está volando hacia el este a$250$ mi/h y el avión B vuela hacia el norte a$300$ mi/h Si ambos se dirigen al mismo aeropuerto, ubicado$30$ millas al este del avión A y$40$ millas al norte del avión B, a qué ritmo es el distancia entre los aviones cambiando?

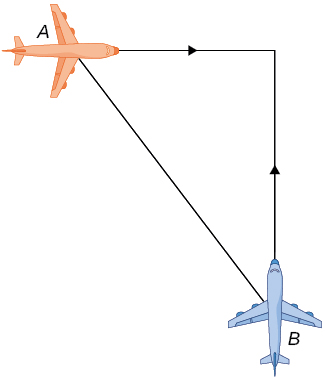
$Un triángulo rectángulo está formado por dos aviones A y B que se mueven perpendicularmente entre sí. La hipotenusa es la distancia entre los planos A y B. Los otros lados son extensiones de la trayectoria de cada plano hasta que se encuentran.$

Contestar: La distancia disminuye a$390$ mi/h.

8) Tú y un amigo van en bicicleta a un restaurante que crees que está al este; tu amigo piensa que el restaurante está al norte. Ambos salen desde el mismo punto, con ustedes montando a$16$ mph este y su amigo viajando$12$ mph hacia el norte. Después de que viajaste$4$ mi, ¿a qué ritmo cambia la distancia entre ustedes?

9) Dos autobuses circulan por autopistas paralelas que están a$5$ mi distancia, uno con dirección este y otro hacia el oeste. Suponiendo que cada autobús conduce una constante$55$ mph, encuentre la velocidad a la que la distancia entre los autobuses está cambiando cuando están a$13$ mi distancia (mientras vuela el cuervo), dirigiéndose uno hacia el otro.

Contestar: La distancia entre ellos se reduce a una velocidad de$\frac{1320}{13}≈101.5$ mph.

10) Una persona de$6$ -pies de altura se aleja de una farola de$10$ -ft a una velocidad constante de$3$ pies/seg. ¿Cuál es la tasa que la punta de la sombra se aleja del poste cuando la persona está a$10$ pies de distancia del poste?

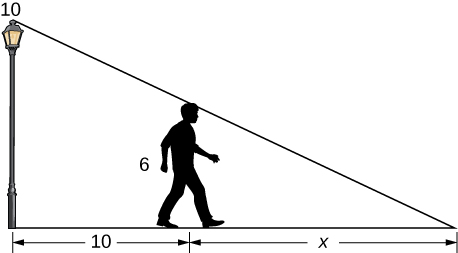
$Se muestra una farola que mide 10 pies de alto. A su derecha, hay una persona que mide 6 pies de altura. Hay una línea desde la parte superior de la farola que toca la parte superior de la cabeza de la persona y luego continúa hasta el suelo. La longitud desde el final de esta línea hasta donde la farola toca el suelo es de 10 + x. La distancia desde la farola a la persona en el suelo es de 10, y la distancia desde la persona hasta el final de la línea es x.$

11) Usando el problema anterior, ¿cuál es la velocidad a la que la punta de la sombra se aleja de la persona cuando la persona está a$10$ pies del poste?

Contestar: $\frac{9}{2}$pies/seg

12) Una persona$5$ de pies de altura camina hacia una pared a una velocidad de$2$ pies/seg. Un foco se encuentra en el suelo a$40$ pies de la pared. ¿Qué tan rápido cambia la altura de la sombra de la persona en la pared cuando la persona está a$10$ pies de la pared?

13) Usando el problema anterior, ¿cuál es la velocidad a la que cambia la sombra cuando la persona está a$10$ pies de la pared, si la persona se aleja de la pared a una velocidad de$2$ pies/seg?

Contestar: Crece a una velocidad$\frac{4}{9}$ pies/seg

14) Un helicóptero que arranca en tierra se eleva directamente al aire a una velocidad de$25$ pies/seg. Estás corriendo en tierra comenzando directamente debajo del helicóptero a una velocidad de$10$ pies/seg. Encuentra la tasa de cambio de la distancia entre el helicóptero y tú mismo después del$5$ sec.

15) Usando el problema anterior, asumiendo que el helicóptero vuelve a subir a una velocidad de$25$ pies/seg y estás corriendo en tierra comenzando directamente debajo del helicóptero a una velocidad de$10$ pies/seg, cuál es la velocidad a la que cambia la distancia entre tú y el helicóptero cuando el helicóptero ha subido a una altura de$60$ ft en el aire, asumiendo que, inicialmente, estaba$30$ ft por encima de ti?

Contestar: La distancia aumenta a$\frac{135\sqrt{26}}{26}$ pies/seg

En los ejercicios 16 - 24, dibuje y etiquete diagramas para ayudar a resolver los problemas de tasas relacionadas.

16) El lado de un cubo aumenta a una velocidad de$\frac{1}{2}$ m/seg. Encuentre la velocidad a la que el volumen del cubo aumenta cuando el lado del cubo es$4$ m.

17) El volumen de un cubo disminuye a una velocidad de$10 \text{ m}^3$ /seg. Encuentre la velocidad a la que cambia el lado del cubo cuando el lado del cubo es$2$ m.

Contestar: $−\frac{5}{6}$m/seg

18) El radio de un círculo aumenta a una velocidad de$2$ m/seg. Encuentre la velocidad a la que el área del círculo aumenta cuando el radio es$5$ m.

19) El radio de una esfera disminuye a una velocidad de$3$ m/seg. Encuentre la velocidad a la que disminuye el área de superficie cuando el radio es$10$ m.

Contestar: $240π \,\text{m}^2\text{/sec}$

20) El radio de una esfera aumenta a una velocidad de$1$ m/seg. Encuentre la velocidad a la que aumenta el volumen cuando el radio es$20$ m.

21) El radio de una esfera está aumentando a una velocidad de$9$ cm/s. Encuentra el radio de la esfera cuando el volumen y el radio de la esfera están aumentando a la misma velocidad numérica.

Contestar: $\frac{1}{2\sqrt{π}}$cm

22) La base de un triángulo se está encogiendo a una velocidad de$1$ cm/min y la altura del triángulo está aumentando a una velocidad de$5$ cm/min. Encuentra la velocidad a la que cambia el área del triángulo cuando la altura es$22$ cm y la base es$10$ cm.

23) Un triángulo tiene dos lados constantes de longitud$3$ ft y$5$ ft. El ángulo entre estos dos lados está aumentando a una velocidad de$0.1$ rad/s. Encuentre la velocidad a la que el área del triángulo está cambiando cuando el ángulo entre los dos lados es$π/6.$

Contestar: El área está aumentando a un ritmo$\frac{3\sqrt{3}}{8}\,\text{ft}^2\text{/sec}$.

24) Un triángulo tiene una altura que está aumentando a una velocidad de$2$ cm/s y su área está aumentando a una velocidad de$4 \,\text{cm}^2\text{/sec}$. Encuentra la velocidad a la que la base del triángulo está cambiando cuando la altura del triángulo es$4$ cm y el área es$20 \,\text{cm}^2$.

En los ejercicios 25 - 27, considera un cono derecho invertido que está goteando agua. (Invertido significa que la punta del cono está orientada hacia abajo, como un embudo). Las dimensiones del tanque cónico son una altura de 16 pies y un radio de 5 pies.

25) ¿Qué tan rápido cambia la profundidad del agua cuando el agua tiene$10$ pies de altura si el cono gotea agua a una velocidad de$10 \,\text{ft}^3\text{/min}$?

Contestar: La profundidad del agua disminuye a$\frac{128}{125π}$ pies/min.

26) Encuentre la velocidad a la que cambia el área de superficie del agua cuando el agua tiene$10$ pies de altura si el cono gotea agua a una velocidad de$10 \,\text{ft}^3\text{/min}$.

27) Si el nivel del agua disminuye a una velocidad de$3$ in/min cuando la profundidad del agua es$8$ ft, determine la velocidad a la que el agua se escapa del cono.

Contestar: El volumen está disminuyendo a una tasa de$\frac{25π}{16}\,\text{ft}^3\text{/min}$.

28) Un cilindro vertical está goteando agua a una velocidad de$1 \,\text{ft}^3\text{/sec}$. Si el cilindro tiene una altura de$10$ pies y un radio de$1$ pies, ¿a qué velocidad cambia la altura del agua cuando la altura es$6$ ft?

29) Un cilindro tiene fugas de agua pero no se puede determinar a qué velocidad. El cilindro tiene una altura de$2$ m y un radio de$2$ m. Encuentre la velocidad a la que el agua se escapa del cilindro si la velocidad a la que disminuye la altura es$10$ cm/min cuando la altura es$1$ m.

Contestar: El agua fluye hacia fuera a ritmo$\frac{2π}{5}\,\text{m}^3\text{/min}$.

30) Un canal tiene extremos en forma de triángulos isósceles, con ancho$3$ m y altura$4$ m, y el canal es de$10$ m de largo. El agua se bombea al canal a una velocidad de$5\,\text{m}^3\text{/min}$. ¿A qué ritmo cambia la altura del agua cuando el agua tiene$1$ m de profundidad?

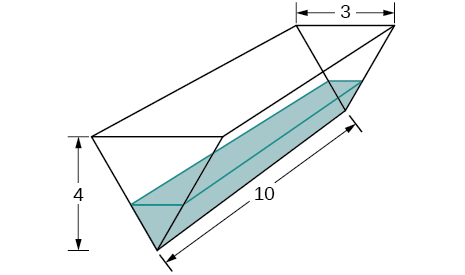
$Se muestra un canal con extremos en forma de triángulos isósceles. Estos triángulos tienen ancho 3 y alto 4. El canal está conformado por rectángulos que son de longitud 10. Hay algo de agua en el abrevadero.$

31) Un tanque tiene la forma de una pirámide cuadrada al revés, con base de$4$ m por$4$ m y una altura de$12$ m (ver la siguiente figura). ¿Qué tan rápido aumenta la altura cuando el agua tiene$2$ m de profundidad si se bombea agua a una velocidad de$\frac{2}{3} \text{ m}^3$ /seg?

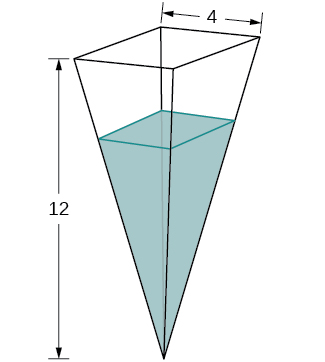
$Se muestra una pirámide cuadrada invertida con longitudes laterales cuadradas 4 y altura 12. Hay una cantidad no especificada de agua dentro de la forma.$

Contestar: $\frac{3}{2}$m/seg

Para los ejercicios 32 - 34, considera una piscina con forma de la mitad inferior de una esfera, que se está llenando a una velocidad de$25 \,\text{ft}^3$ /min. El radio de la piscina es de$10$ pies.

32) Encuentre la velocidad a la que la profundidad del agua está cambiando cuando el agua tiene una profundidad de$5$ pies.

33) Encuentre la velocidad a la que la profundidad del agua está cambiando cuando el agua tiene una profundidad de$1$ pies.

Contestar: $\frac{25}{19π}$pies/min

34) Si la altura aumenta a una velocidad de$1$ in/seg cuando la profundidad del agua es$2$ ft, encuentre la velocidad a la que se bombea el agua.

35) La grava se está descargando de un camión y cae en una pila con forma de cono a una velocidad de$10 \,\text{ft}^3/\text{min}$. El radio de la base del cono es tres veces la altura del cono. Encuentre la velocidad a la que cambia la altura de la grava cuando la pila tiene una altura de$5$ pies.

Contestar: $\frac{2}{45π}$pies/min

36) Usando una configuración similar al problema anterior, encuentre la velocidad a la que se está descargando la grava si el pilote tiene$5$ pies de altura y la altura aumenta a una velocidad de$4$ in/min.

En los ejercicios 37 - 41, dibujar las situaciones y resolver los problemas de tasa relacionada.

37) Estás parado en el suelo y estás observando a un pájaro volar horizontalmente a una velocidad de$10$ m/seg. El ave se encuentra$40$ m por encima de tu cabeza. ¿Qué tan rápido cambia el ángulo de elevación cuando la distancia horizontal entre usted y el ave es$9$ m?

Contestar: El ángulo disminuye a$\frac{400}{1681}$ rad/seg.

38) Te paras a$40$ pies de un cohete de botella en el suelo y observa cómo despega verticalmente hacia el aire a una velocidad de$20$ pies/seg. Encuentra la velocidad a la que cambia el ángulo de elevación cuando el cohete tiene$30$ pies en el aire.

39) Un faro,$L$, se encuentra en una isla a$4$ mi distancia del punto más cercano$P$,, en la playa (ver la siguiente imagen). Si la luz del faro gira en el sentido de las agujas del reloj a un ritmo constante de$10$ revoluciones/min, ¿qué tan rápido se mueve el rayo de luz a través de la playa a$2$ mi distancia del punto más cercano de la playa?

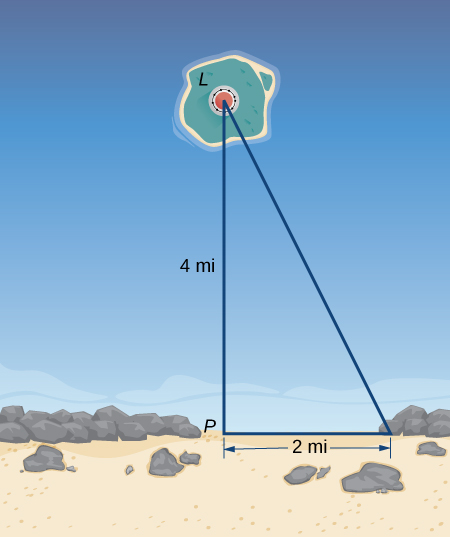
$Un triángulo rectángulo está formado por un faro L, un punto P en la orilla que es perpendicular a la línea del faro a la orilla, y un punto 2 millas a la derecha del punto P. La distancia de P a L es de 4 millas.$

Contestar: $100π$mi/min

40) Usando la misma configuración que el problema anterior, determinar a qué velocidad el haz de luz se mueve a través de la playa a$1$ mi distancia del punto más cercano de la playa.

41) Estás caminando a una parada de autobús en esquina recta. Se mueve hacia el norte a una velocidad de$2$ m/seg y se encuentra$20$ m al sur de la intersección. El autobús viaja hacia el oeste a una velocidad de$10$ m/seg lejos de la intersección — ¡te has perdido el autobús! ¿Cuál es la velocidad a la que cambia el ángulo entre usted y el autobús cuando está$20$ m al sur de la intersección y el autobús está$10$ m al oeste de la intersección?

Contestar: El ángulo está cambiando a una velocidad de$\frac{11}{25}$ rad/s.

En los ejercicios 42 - 45, se refieren a la figura de diamante de béisbol, que tiene lados de 90 pies.

$Se muestra un campo de béisbol, con las bases etiquetadas como Home, 1st, 2nd y 3rd haciendo un cuadrado con longitudes laterales de 90 pies.$

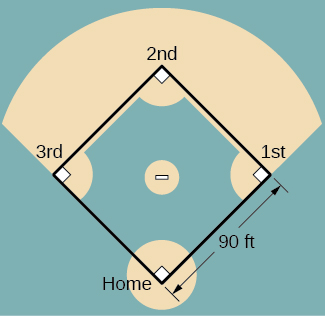
42) [T] Un bateador golpea una pelota hacia la tercera base a$75$ pies/seg y corre hacia la primera base a una velocidad de$24$ pies/seg. ¿A qué ritmo cambia la distancia entre el balón y el bateador cuando han pasado los$2$ segundos?

43) [T] Un bateador golpea una pelota hacia la segunda base a$80$ pies/seg y corre hacia la primera base a una velocidad de$30$ pies/seg. ¿A qué ritmo cambia la distancia entre el balón y el bateador cuando el corredor ha cubierto un tercio de la distancia hasta la primera base? (Pista: Recordemos la ley de los cosenos.)

Contestar: La distancia está aumentando a una velocidad de$62.50$ pies/seg.

44) [T] Un bateador golpea la pelota y corre hacia la primera base a una velocidad de$22$ pies/seg. ¿A qué velocidad cambia la distancia entre el corredor y la segunda base cuando el corredor ha corrido$30$ ft?

45) [T] Los corredores comienzan en primera y segunda base. Cuando se golpea el beisbol, el corredor de primera base corre a una velocidad de$18$ pies/seg hacia la segunda base y el corredor en la segunda base corre a una velocidad de$20$ pies/seg hacia la tercera base. ¿Qué tan rápido cambia la distancia entre corredores 1 seg después de golpear la pelota?

Contestar: La distancia está disminuyendo a una velocidad de$11.99$ pies/seg.