4.6E: Ejercicios para la Sección 4.6

Última actualización
Guardar como PDF

Page ID: 116521

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Para los ejercicios 1 - 5, examine las gráficas. Identificar dónde se encuentran las asíntotas verticales.

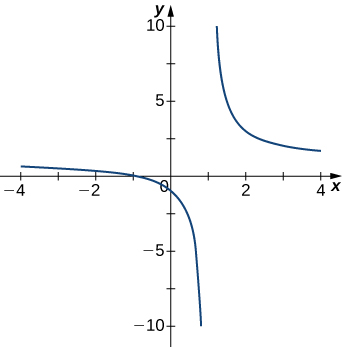
$La función graficada disminuye muy rápidamente a medida que se acerca a x = 1 desde la izquierda, y al otro lado de x = 1, parece comenzar cerca del infinito y luego disminuir rápidamente.$

Contestar: $x=1$

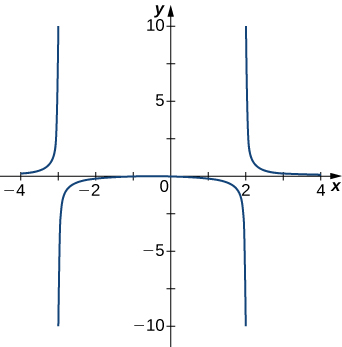
$La función graficada aumenta muy rápidamente a medida que se acerca a x = −3 desde la izquierda, y en el otro lado de x = −3, parece comenzar cerca del infinito negativo y luego aumentar rápidamente para formar una especie de forma de U que apunta hacia abajo, con el otro lado de la U en x = 2. Al otro lado de x = 2, la gráfica parece comenzar cerca del infinito y luego disminuir rápidamente.$

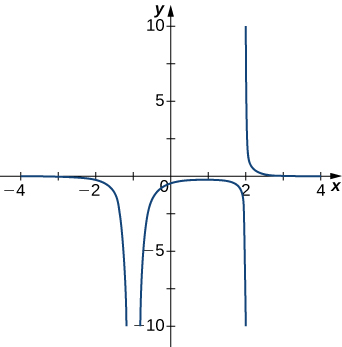
$La función graficada disminuye muy rápidamente a medida que se acerca a x = −1 desde la izquierda, y en el otro lado de x = −1, parece comenzar cerca del infinito negativo y luego aumentar rápidamente para formar una especie de forma de U que apunta hacia abajo, con el otro lado de la U en x = 2. Al otro lado de x = 2, la gráfica parece comenzar cerca del infinito y luego disminuir rápidamente.$

Contestar: $x=−1,\;x=2$

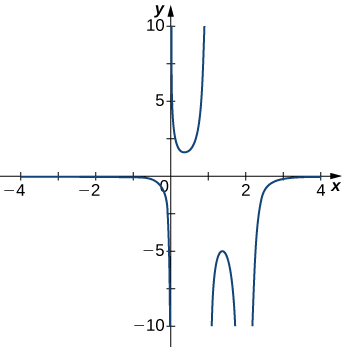
$La función graficada disminuye muy rápidamente a medida que se acerca a x = 0 desde la izquierda, y en el otro lado de x = 0, parece comenzar cerca del infinito y luego disminuir rápidamente para formar una especie de forma de U que apunta hacia arriba, con el otro lado de la U en x = 1. En el otro lado de x = 1, hay otra forma de U apuntando hacia abajo, con su otro lado en x = 2. En el otro lado de x = 2, la gráfica parece comenzar cerca del infinito negativo y luego aumentar rápidamente.$

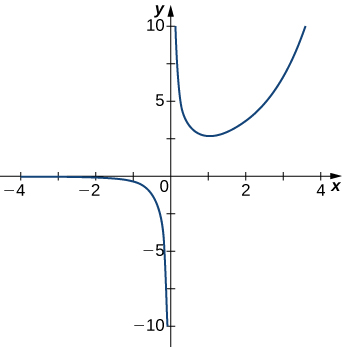
$La función graficada disminuye muy rápidamente a medida que se acerca a x = 0 desde la izquierda, y en el otro lado de x = 0, parece comenzar cerca del infinito y luego disminuir rápidamente para formar una especie de forma de U que está apuntando hacia arriba, siendo el otro lado una función normal que aparece como si tomara la totalidad del valores del eje x.$

Contestar: $x=0$

Para las funciones$f(x)$ en los ejercicios 6 - 10, determinar si hay una asíntota en$x=a$. Justifica tu respuesta sin graficar en una calculadora.

6)$f(x)=\dfrac{x+1}{x^2+5x+4},\quad a=−1$

7)$f(x)=\dfrac{x}{x−2},\quad a=2$

Contestar: Sí, hay una asíntota vertical en$x = 2$.

8)$f(x)=(x+2)^{3/2},\quad a=−2$

9)$f(x)=(x−1)^{−1/3},\quad a=1$

Contestar: Sí, hay asíntota vertical en$x = 1$.

10)$f(x)=1+x^{−2/5},\quad a=1$

En los ejercicios 11 - 20, evaluar el límite.

11)$\displaystyle \lim_{x→∞}\frac{1}{3x+6}$

Contestar: $\displaystyle \lim_{x→∞}\frac{1}{3x+6} = 0$

12)$\displaystyle \lim_{x→∞}\frac{2x−5}{4x}$

13)$\displaystyle \lim_{x→∞}\frac{x^2−2x+5}{x+2}$

Contestar: $\displaystyle \lim_{x→∞}\frac{x^2−2x+5}{x+2} = ∞$

14)$\displaystyle \lim_{x→−∞}\frac{3x^3−2x}{x^2+2x+8}$

15)$\displaystyle \lim_{x→−∞}\frac{x^4−4x^3+1}{2−2x^2−7x^4}$

Contestar: $\displaystyle \lim_{x→−∞}\frac{x^4−4x^3+1}{2−2x^2−7x^4} = −\frac{1}{7}$

16)$\displaystyle \lim_{x→∞}\frac{3x}{\sqrt{x^2+1}}$

17)$\displaystyle \lim_{x→−∞}\frac{\sqrt{4x^2−1}}{x+2}$

Contestar: $\displaystyle \lim_{x→−∞}\frac{\sqrt{4x^2−1}}{x+2} = -2$

18)$\displaystyle \lim_{x→∞}\frac{4x}{\sqrt{x^2−1}}$

19)$\displaystyle \lim_{x→−∞}\frac{4x}{\sqrt{x^2−1}}$

Contestar: $\displaystyle \lim_{x→−∞}\frac{4x}{\sqrt{x^2−1}} = -4$

20)$\displaystyle \lim_{x→∞}\frac{2\sqrt{x}}{x−\sqrt{x}+1}$

Para los ejercicios 21 - 25, encuentra las asíntotas horizontales y verticales.

21)$f(x)=x−\dfrac{9}{x}$

Contestar: Horizontal: ninguno,
Vertical:$x=0$

22)$f(x)=\dfrac{1}{1−x^2}$

23)$f(x)=\dfrac{x^3}{4−x^2}$

Contestar: Horizontal: ninguno,
Vertical:$x=±2$

24)$f(x)=\dfrac{x^2+3}{x^2+1}$

25)$f(x)=\sin(x)\sin(2x)$

Contestar: Horizontal: ninguno,
Vertical: ninguno

26)$f(x)=\cos x+\cos(3x)+\cos(5x)$

27)$f(x)=\dfrac{x\sin(x)}{x^2−1}$

Contestar: Horizontal:$y=0,$
Vertical:$x=±1$

28)$f(x)=\dfrac{x}{\sin(x)}$

29)$f(x)=\dfrac{1}{x^3+x^2}$

Contestar: Horizontal:$y=0,$
Vertical:$x=0$ y$x=−1$

30)$f(x)=\dfrac{1}{x−1}−2x$

31)$f(x)=\dfrac{x^3+1}{x^3−1}$

Contestar: Horizontal:$y=1,$
Vertical:$x=1$

32)$f(x)=\dfrac{\sin x+\cos x}{\sin x−\cos x}$

33)$f(x)=x−\sin x$

Contestar: Horizontal: ninguno,
Vertical: ninguno

34)$f(x)=\dfrac{1}{x}−\sqrt{x}$

Para los ejercicios 35 - 38, construir una función$f(x)$ que tenga las asíntotas dadas.

35)$x=1$ y$y=2$

Contestar: Las respuestas variarán, por ejemplo:$y=\dfrac{2x}{x−1}$

36)$x=1$ y$y=0$

37)$y=4, \;x=−1$

Contestar: Las respuestas variarán, por ejemplo:$y=\dfrac{4x}{x+1}$

38)$x=0$

En los ejercicios 39 - 43, grafica la función en una calculadora gráfica en la ventana$x=[−5,5]$ y estima la asíntota o límite horizontal. Después, calcule la asíntota o límite horizontal real.

39) [T]$f(x)=\dfrac{1}{x+10}$

Contestar: $\displaystyle \lim_{x→∞}\frac{1}{x+10}=0$así$f$ tiene una asíntota horizontal de$y=0$.

40) [T]$f(x)=\dfrac{x+1}{x^2+7x+6}$

41) [T]$\displaystyle \lim_{x→−∞}x^2+10x+25$

Contestar: $\displaystyle \lim_{x→−∞}x^2+10x+25 = ∞$

42) [T]$\displaystyle \lim_{x→−∞}\frac{x+2}{x^2+7x+6}$

43) [T]$\displaystyle \lim_{x→∞}\frac{3x+2}{x+5}$

Contestar: $\displaystyle \lim_{x→∞}\frac{3x+2}{x+5}=3$por lo que esta función tiene una asíntota horizontal de$y=3$.

En los ejercicios 44 - 55, dibuja una gráfica de las funciones sin usar una calculadora. Asegúrese de notar todas las características importantes de la gráfica: máximos y mínimos locales, puntos de inflexión y comportamiento asintótico.

44)$y=3x^2+2x+4$

45)$y=x^3−3x^2+4$

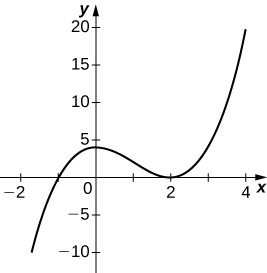
Contestar: $La función comienza en el tercer cuadrante, aumenta para pasar a través (−1, 0), aumenta a un máximo e e intercepta a 4, disminuye al tacto (2, 0), y luego aumenta a (4, 20).$

46)$y=\dfrac{2x+1}{x^2+6x+5}$

47)$y=\dfrac{x^3+4x^2+3x}{3x+9}$

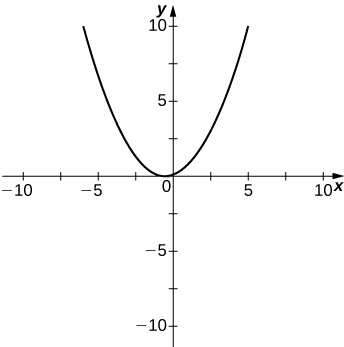
Contestar: $Parábola orientada hacia arriba con mínimo entre x = 0 y x = −1 con y intercepción entre 0 y 1.$

48)$y=\dfrac{x^2+x−2}{x^2−3x−4}$

49)$y=\sqrt{x^2−5x+4}$

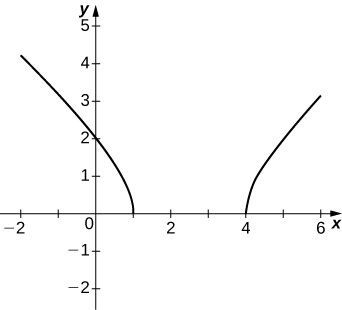
Contestar: $Esta gráfica comienza en (−2, 4) y disminuye de manera convexa a (1, 0). Entonces la gráfica comienza de nuevo en (4, 0) y aumenta de manera convexa a (6, 3).$

50)$y=2x\sqrt{16−x^2}$

51)$y=\dfrac{\cos x}{x}$, el$x=[−2π,2π]$

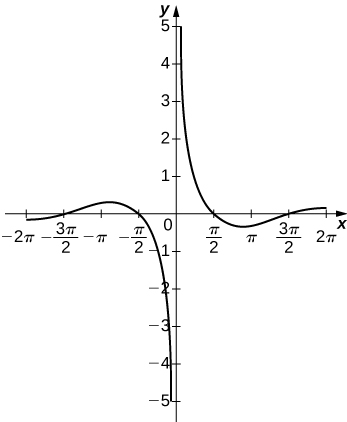
Contestar: $Esta gráfica tiene asíntota vertical en x = 0. La primera parte de la función ocurre en el segundo y tercer cuadrantes y comienza en el tercer cuadrante justo debajo (−2π, 0), aumenta y pasa por el eje x en −3π/2, alcanza un máximo y luego disminuye a través del eje x en −π/2 antes de acercarse a la asíntota. Al otro lado de la asíntota, la función inicia en el primer cuadrante, disminuye rápidamente para pasar por π/2, disminuye a un mínimo local y luego aumenta a través de (3π/2, 0) antes de permanecer justo por encima (2π, 0).$

52)$y=e^x−x^3$

53)$y=x\tan x, \quad x=[−π,π]$

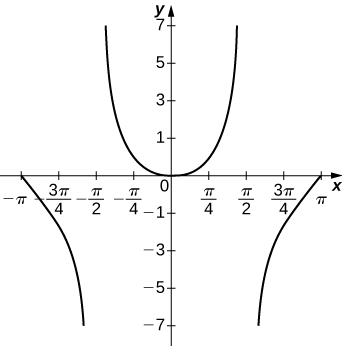
Contestar: $Esta gráfica tiene asíntotas verticales a x = ±π/2. La gráfica es simétrica alrededor del eje y, por lo que describir el lado izquierdo será suficiente. La función comienza en (−π, 0) y disminuye rápidamente a la asíntota. Después se inicia en el otro lado de la asíntota en el segundo cuadrante y disminuye al origen.$

54)$y=x\ln(x), \quad x>0$

55)$y=x^2\sin(x),\quad x=[−2π,2π]$

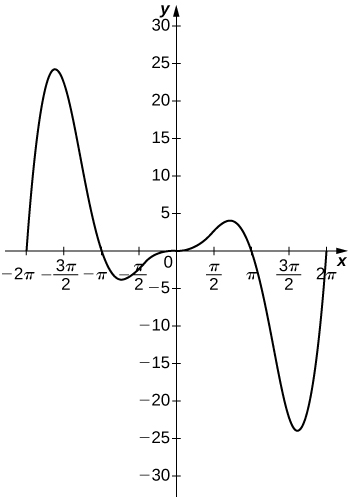
Contestar: $Esta función comienza en (−2π, 0), aumenta a cerca (−3π/2, 25), disminuye a través de (−π, 0), logra un mínimo local y luego aumenta a través del origen. Al otro lado del origen, la gráfica es la misma pero volteada, es decir, es congruente con la otra mitad por una rotación de 180 grados.$

56) ¿$f(x)=\dfrac{P(x)}{Q(x)}$Para tener una asíntota en$y=2$ ese momento los polinomios$P(x)$ y$Q(x)$ debe tener qué relación?

57)$f(x)=\dfrac{P(x)}{Q(x)}$ Para tener una asíntota en$x=0$, entonces los polinomios$P(x)$ y$Q(x).$ deben tener ¿qué relación?

Contestar: $Q(x).$debe tener$x^{k+1}$ como factor, donde$P(x)$ tiene$x^k$ como factor.

58) Si$f′(x)$ tiene asíntotas en$y=3$ y$x=1$, entonces ¿qué asíntotas$f(x)$ tiene?

59) Ambos$f(x)=\dfrac{1}{x−1}$ y$g(x)=\dfrac{1}{(x−1)^2}$ tienen asíntotas en$x=1$ y$y=0.$ ¿Cuál es la diferencia más obvia entre estas dos funciones?

Contestar: $\displaystyle \lim_{x→1^−}f(x)=-\infty \text{ and } \lim_{x→1^−}g(x)=\infty$

60) Verdadero o falso: Cada proporción de polinomios tiene asíntotas verticales.