4.7E: Ejercicios para la Sección 4.7

Última actualización
Guardar como PDF

Page ID: 116368

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Para los ejercicios 1 - 4, conteste por prueba, contraejemplo o explicación.

1) Cuando encuentras el máximo para un problema de optimización, ¿por qué necesitas verificar el signo de la derivada alrededor de los puntos críticos?

Contestar: Los puntos críticos pueden ser los mínimos, máximos o ninguno.

2) ¿Por qué es necesario verificar los endpoints en busca de problemas de optimización?

3) Verdadero o Falso. Para cada función no lineal continua, puede encontrar el valor$x$ que maximiza la función.

Contestar: Falso; solo$y=−x^2$ tiene un mínimo

4) Verdadero o Falso. Por cada función continua no constante en un dominio cerrado y finito, existe al menos una$x$ que minimiza o maximiza la función.

En los ejercicios 5 a 8, configurar y evaluar cada problema de optimización.

5) Para llevar una maleta en un avión, el$\text{length}+\text{width}+\text{height}$ de la caja debe ser menor o igual a$62$ adentro. Asumiendo que la altura es fija, muestra que el volumen máximo es$V=h\left(31−\frac{1}{2}h\right)^2.$ ¿Qué altura te permite tener el mayor volumen?

Contestar: $h=\frac{62}{3}$en.

6) Estás construyendo una caja de cartón con las dimensiones$2$ m por$4$ m. Luego cortas cuadrados de igual tamaño de cada esquina para que puedas doblar los bordes. ¿Cuáles son las dimensiones de la caja con mayor volumen?

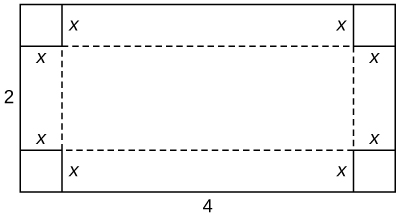
$Se dibuja un rectángulo con alto 2 y ancho 4. Cada esquina tiene un cuadrado con la longitud lateral x marcada en ella.$

7) Encuentra el entero positivo que minimiza la suma del número y su recíproco.

Contestar: $1$

8) Encontrar dos enteros positivos de tal manera que su suma sea$10$, y minimizar y maximizar la suma de sus cuadrados.

En los ejercicios 9 - 11, considere la construcción de una pluma para encerrar un área.

9) Tiene$400\,\text{ft}$ de cercado para construir un corral rectangular para ganado. ¿Cuáles son las dimensiones de la pluma que maximizan el área?

Contestar: $100\,\text{ft}$por$100\,\text{ft}$

10) Tienes$800\,\text{ft}$ de esgrima para hacer una pluma para cerdos. Si tienes un río a un lado de tu propiedad, ¿cuál es la dimensión de la pluma rectangular que maximiza el área?

11) Es necesario construir una barda alrededor de un área de$1600\,\text{ft}^2$. ¿Cuáles son las dimensiones de la pluma rectangular para minimizar la cantidad de material necesario?

Contestar: $40\,\text{ft}$por$40\,\text{ft}$

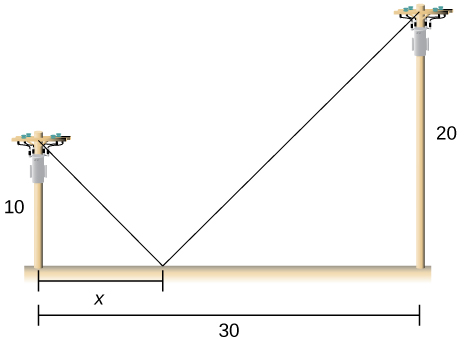
12) Dos polos están conectados por un cable que también está conectado a tierra. El primer poste es$20\,\text{ft}$ alto y el segundo poste es$10\,\text{ft}$ alto. Hay una distancia de$30\,\text{ft}$ entre los dos polos. ¿Dónde se debe anclar el cable a tierra para minimizar la cantidad de cable necesario?

$Se muestran dos postes, uno que mide 10 de alto y el otro de 20 de alto. Se hace un triángulo rectángulo con el poste más corto con otro lado de longitud x. La distancia entre los dos polos es de 30.$

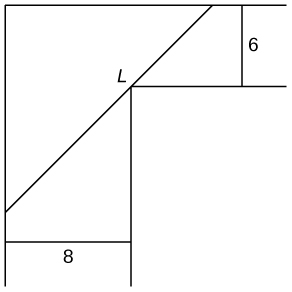
13) [T] Te estás mudando a un nuevo departamento y notarás que hay una esquina donde el pasillo se estrecha de$8\,\text{ft}$ a$6\,\text{ft}$. ¿Cuál es la longitud del artículo más largo que se puede llevar horizontalmente a la vuelta de la esquina?

$Se dibuja una figura al revés en forma de L con la parte _ de 6 de ancho y la | parte de 8 de ancho. Hay una línea dibujada de la _ parte a la | parte que toca la esquina cercana de la forma para formar una hipotenusa para un triángulo rectángulo siendo los otros lados el resto de las partes _ y |. Esta línea está marcada con L.$

Contestar: $19.73\,\text{ft}$

14) El pulso de un paciente mide$70 \,\text{bpm},\, 80 \,\text{bpm}$, entonces$120 \,\text{bpm}$. Para determinar una medición precisa del pulso, ¿el médico quiere saber qué valor minimiza la expresión$(x−70)^2+(x−80)^2+(x−120)^2$? ¿Qué valor lo minimiza?

15) En el problema anterior, supongamos que el paciente estuvo nervioso durante la tercera medición, por lo que solo pesamos ese valor a la mitad que los demás. ¿Cuál es el valor que minimiza$(x−70)^2+ (x−80)^2+\frac{1}{2}(x−120)^2?$

Contestar: $84 \,\text{bpm}$

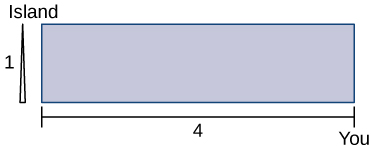
16) Se puede correr a una velocidad de$6$ mph y nadar a una velocidad de$3$ mph y se encuentra en la orilla,$4$ millas al este de una isla que está$1$ milla al norte de la costa. ¿Hasta dónde debes correr hacia el oeste para minimizar el tiempo necesario para llegar a la isla?

$Se dibuja un rectángulo que tiene altura 1 y longitud 4. En la esquina inferior derecha, está marcada como “Tú” y en la esquina superior izquierda está marcada como “Isla”.$

Para los ejercicios 17 - 19, considere un socorrista en una alberca circular con diámetro$40$ m. Debe llegar a alguien que se esté ahogando exactamente en el lado opuesto de la alberca, en posición$C$. El socorrista nada a velocidad$v$ y corre alrededor de la piscina a gran velocidad$w=3v.$

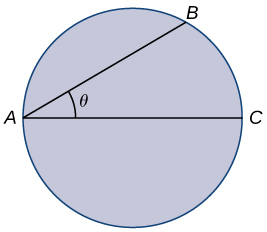
$Se dibuja un círculo con los puntos A y C sobre un diámetro. Hay un punto B dibujado en el círculo tal que el ángulo BAC forma un ángulo agudo θ.$

17) Encontrar una función que mida la cantidad total de tiempo que tarda en llegar a la persona que se ahoga en función del ángulo de nado,$θ$.

Contestar: $T(θ)=\dfrac{40θ}{3v}+\dfrac{40\cos θ}{v}$

18) Encuentra en qué ángulo debe nadar$θ$ el socorrista para llegar a la persona que se ahoga en el menor tiempo posible.

19) Un camión utiliza gas como$g(v)=av+\dfrac{b}{v}$, donde$v$ representa la velocidad del camión y$g$ representa los galones de combustible por milla. ¿A qué velocidad se minimiza el consumo de combustible?

Contestar: $v=\sqrt{\dfrac{b}{a}}$

Para los ejercicios 20 - 21, considere una limusina que llegue$m(v)=\frac{120−2v}{5}\,\text{mi/gal}$ a velocidad$v$, el chofer cuesta$$15/\text{h}$, y la gasolina es$$3.50/\text{gal}$.

20) Encuentra el costo por milla a velocidad$v.$

21) Encuentra la velocidad de conducción más barata.

Contestar: aproximadamente$34.02$ mph

Para los ejercicios 22 - 24, considere una pizzería que venda pizzas por un ingreso de$R(x)=ax$ y costos$C(x)=b+cx+dx^2$, donde$x$ representa el número de pizzas.

22) Encuentra la función de ganancia por el número de pizzas. ¿Cuántas pizzas da el mayor beneficio por pizza?

23) Supongamos que$R(x)=10x$ y$C(x)=2x+x^2$. ¿Cuántas pizzas vendidas maximiza la ganancia?

Contestar: La venta de$4$ pizzas maximizará la ganancia.

24) Supongamos que$R(x)=15x$, y$C(x)=60+3x+\frac{1}{2}x^2$. ¿Cuántas pizzas vendidas maximiza la ganancia?

Para los ejercicios 25 - 26, considere un alambre de$4$ pies de largo cortado en dos piezas. Una pieza forma un círculo con radio$r$ y la otra forma un cuadrado de lado$x$.

25) Elegir$x$ maximizar la suma de sus áreas.

Contestar: $x = 0$

26) Elegir$x$ minimizar la suma de sus áreas.

Para los ejercicios 27 - 30, considere dos números no negativos$x$ y$y$ tal que$x+y=10$. Maximizar y minimizar las cantidades.

27)$xy$

Contestar: Máximo:$x=5,\,y=5;$
Mínimo:$x=0,\,y=10$ y$y=0,\,x=10$

28$x^2y^2$

29)$y−\dfrac{1}{x}$

Contestar: Máximo:$x=1,\,y=9;$
Mínimo: ninguno

30)$x^2−y$

En los ejercicios 31 - 36, dibujar el problema de optimización dado y resolver.

31) Encuentra el volumen del cilindro circular derecho más grande que cabe en una esfera de radio$1$.

Contestar: $V = \frac{4π}{3\sqrt{3}}$

32) Encuentra el volumen del cono derecho más grande que cabe en una esfera de radio$1$.

33) Encuentra el área del rectángulo más grande que encaja en el triángulo con lados$x=0,\,y=0$ y$\dfrac{x}{4}+\dfrac{y}{6}=1.$

Contestar: $A = 6$

34) Encuentra el mayor volumen de un cilindro que cabe en un cono que tiene radio base$R$ y altura$h$.

35) Encuentre las dimensiones del volumen del cilindro cerrado$V=16π$ que tenga la menor cantidad de área superficial.

Contestar: $r=2,\,h=4$

36) Encuentra las dimensiones de un cono derecho con área de superficie$S=4π$ que tiene el mayor volumen.

Para los ejercicios 37 - 40, considere los puntos en las gráficas de las ecuaciones dadas. Usa una calculadora para graficar las funciones.

37) [T] ¿Dónde está la línea$y=5−2x$ más cercana al origen?

Contestar: $(2,1)$

38) [T] ¿Dónde está la línea$y=5−2x$ más cercana al punto$(1,1)$?

39) [T] ¿Dónde está la parábola$y=x^2$ más cercana al punto$(2,0)$?

Contestar: $(0.8351,0.6974)$

40) [T] ¿Dónde está la parábola$y=x^2$ más cercana al punto$(0,3)$?

En los ejercicios 41 - 45, configurar, pero no evaluar, cada problema de optimización.

41) Una ventana está compuesta por un semicírculo colocado encima de un rectángulo. Si tienes$20\,\text{ft}$ materiales para enmarcar ventanas para el marco exterior, ¿cuál es el tamaño máximo de la ventana que puedes crear? Use r para representar el radio del semicírculo.

$Se dibuja una ventana semicircular con radio r.$

Contestar: $A=20r−2r^2−\frac{1}{2}πr^2$

42) Tienes una hilera de plantas de$20$ sandía de jardín que producen un promedio de$30$ sandías cada una. Para cualquier planta de sandía adicional plantada, la producción por planta de sandía cae en una sandía. ¿Cuántas plantas de sandía adicionales deberías plantar?

43) Estás construyendo una caja para que tu gato duerma. El material de felpa para el fondo cuadrado de la caja cuesta$$5/\text{ft}^2$ y el material para los lados cuesta$$2/\text{ft}^2$. Necesitas una caja con volumen$4\,\text{ft}^3$. Encuentra las dimensiones de la caja que minimizan el costo. Se usa$x$ para representar la longitud del lado de la caja.

Contestar: $C(x)=5x^2+\dfrac{32}{x}$

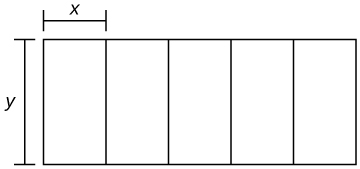
44) Está construyendo cinco plumas idénticas adyacentes entre sí con un área total de$1000\,\text{m}^2$, como se muestra en la siguiente figura. ¿Qué dimensiones debes usar para minimizar la cantidad de cercas?

$Un rectángulo se divide en cinco secciones, y cada sección tiene longitud y y ancho x.$

45) Eres el encargado de un complejo de departamentos con$50$ unidades. Cuando establece la renta en$$800/\text{month}$, se rentan todos los departamentos. A medida que aumenta la renta por$$25/\text{month}$, se renta un departamento menos. Los costos de mantenimiento corren$$50/\text{month}$ por cada unidad ocupada. ¿Cuál es la renta que maximiza la cantidad total de ganancias?

Contestar: $P(x)=(50−x)(800+25x−50)$

Search

Text Color

Text Size

Margin Size

Font Type