5.1E: Ejercicios para la Sección 5.1

Última actualización
Guardar como PDF

Page ID: 116204

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1.) Indicar si las sumas dadas son iguales o desiguales.

$\displaystyle \sum_{i=1}^{10}i$y$\displaystyle \sum_{k=1}^{10}k$
$\displaystyle \sum_{i=1}^{10}i$y$\displaystyle \sum_{i=6}^{15}(i−5)$
$\displaystyle \sum_{i=1}^{10}i(i−1)$y$\displaystyle \sum_{j=0}^9(j+1)j$
$\displaystyle \sum_{i=1}^{10}i(i−1)$y$\displaystyle \sum_{k=1}^{10}(k^2−k)$

Contestar: a. Son iguales; ambos representan la suma de los primeros 10 números enteros.
b. Son iguales; ambos representan la suma de los primeros 10 números enteros.
c. Son iguales sustituyendo$\displaystyle j=i−1.$
d. Son iguales; la primera suma factores los términos de la segunda.

En los ejercicios 2 - 3, usa las reglas para sumas de potencias de enteros para calcular las sumas.

2)$\displaystyle \sum_{i=5}^{10}i$

3)$\displaystyle \sum_{i=5}^{10}i^2$

Contestar: $\displaystyle \sum_{i=5}^{10}i^2 = 385−30=355$

Supongamos que$\displaystyle \sum_{i=1}^{100}a_i=15$ y$\displaystyle \sum_{i=1}^{100}b_i=−12.$

En los ejercicios 4 - 7, computar las sumas.

4)$\displaystyle \sum_{i=1}^{100}(a_i+b_i)$

5)$\displaystyle \sum_{i=1}^{100}(a_i−b_i)$

Contestar: $\displaystyle \sum_{i=1}^{100}(a_i−b_i) = 15−(−12)=27$

6)$\displaystyle \sum_{i=1}^{100}(3a_i−4b_i)$

7)$\displaystyle \sum_{i=1}^{100}(5a_i+4b_i)$

Contestar: $\displaystyle \sum_{i=1}^{100}(5a_i+4b_i) = 5(15)+4(−12)=27$

En los ejercicios 8 - 11, use propiedades de suma y fórmulas para reescribir y evaluar las sumas.

8)$\displaystyle \sum_{k=1}^{20}100(k^2−5k+1)$

9)$\displaystyle \sum_{j=1}^{50}(j^2−2j)$

Contestar: $\displaystyle \sum_{j=1}^{50}j^2−2\sum_{j=1}^{50}j=\frac{(50)(51)(101)}{6}−\frac{2(50)(51)}{2}=40, 375$

10)$\displaystyle \sum_{j=11}^{20}(j^2−10j)$

11)$\displaystyle \sum_{k=1}^{25}[(2k)^2−100k]$

Contestar: $\displaystyle 4\sum_{k=1}^{25}k^2−100\sum_{k=1}^{25}k=\frac{4(25)(26)(51)}{9}−50(25)(26)=−10, 400$

Let$L_n$ denotar la suma del extremo izquierdo usando n subintervalos y let$R_n$ denotar la suma correspondiente del extremo derecho.

En los ejercicios 12 - 19, compute las sumas indicadas izquierda y derecha para las funciones dadas en el intervalo indicado.

12)$L_4$ para$ f(x)=\dfrac{1}{x−1}$ el$ [2,3]$

13)$ R_4$ para$ g(x)=\cos(πx)$ el$ [0,1]$

Contestar: $R_4=0.25$

14)$ L_6$ para$ f(x)=\dfrac{1}{x(x−1)}$ el$ [2,5]$

15)$ R_6$ para$ f(x)=\dfrac{1}{x(x−1)}$ el$ [2,5]$

Contestar: $ R_6=0.372$

16)$ R_4$ para$ \dfrac{1}{x^2+1}$ el$ [−2,2]$

17)$ L_4$ para$ \dfrac{1}{x^2+1}$ el$ [−2,2]$

Contestar: $ L_4=2.20$

18)$ R_4$ para$ x^2−2x+1$ el$ [0,2]$

19)$ L_8$ para$ x^2−2x+1$ el$ [0,2]$

Contestar: $ L_8=0.6875$

20) Calcular las sumas de Riemann izquierda y derecha—$ L_4$ y$ R_4$, respectivamente, para$ f(x)=(2−|x|)$ en$ [−2,2].$ Calcular su valor promedio y compararlo con el área bajo la gráfica de$f$.

21) Calcular las sumas de Riemann izquierda y derecha—$ L_6$ y$ R_6$, respectivamente, para$ f(x)=(3−|3−x|)$ en$ [0,6].$ Calcular su valor promedio y compararlo con el área bajo la gráfica de$f$.

Contestar: $ L_6=9.000=R_6$. La gráfica de$f$ es un triángulo con área$9\,\text{units}^2$.

22) Calcular las sumas de Riemann izquierda$ L_4$ y derecha y$ R_4$, respectivamente, para$ f(x)=\sqrt{4−x^2}$ on$ [−2,2]$ y comparar sus valores.

23) Calcular las sumas de Riemann izquierda$ L_6$ y derecha y$ R_6$, respectivamente, para$ f(x)=\sqrt{9−(x−3)^2}$ on$ [0,6]$ y comparar sus valores.

Contestar: $L_6=13.12899=R_6$. Ellos son iguales.

Para los ejercicios 24 - 27, exprese las siguientes sumas de punto final en notación sigma pero no las evalúe.

24)$ L_{30}$ para$ f(x)=x^2$ el$ [1,2]$

25)$ L_{10}$ para$ f(x)=\sqrt{4−x^2}$ el$ [−2,2]$

Contestar: $\displaystyle L_{10}=\frac{4}{10}\sum_{i=1}^{10}\sqrt{4−(−2+4\frac{(i−1)}{10})}$

26)$ R_{20}$ para$ f(x)=\sin x$ el$ [0,π]$

27)$ R_{100}$ para$\ln x$ el$[1,e]$

Contestar: $\displaystyle R_{100}=\frac{e−1}{100}\sum_{i=1}^{100}ln(1+(e−1)\frac{i}{100})$

En los ejercicios 28 - 33, grafica la función luego usa una calculadora o un programa de computadora para evaluar las siguientes sumas de punto final izquierda y derecha. ¿Es el área bajo la curva entre las sumas del punto final izquierdo y derecho?

28) [T]$ L_{100}$ y$ R_{100}$ para$ y=x^2−3x+1$ en el intervalo$ [−1,1]$

29) [T]$ L_{100}$ y$R_{100}$ para$y=x^2$ en el intervalo$[0,1]$

Contestar

$alt$

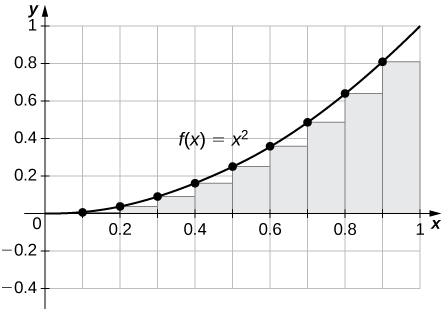
$R_{100}=0.33835,\quad L_{100}=0.32835.$
La trama muestra que la suma de Riemann izquierda es una subestimación porque la función va en aumento. De igual manera, la suma correcta de Riemann es una sobreestimación. El área se encuentra entre las sumas de Riemann izquierda y derecha. Se muestran diez rectángulos para mayor claridad visual. Este comportamiento persiste para más rectángulos.

30) [T]$L_{50}$ y$R_{50}$ para$y=\dfrac{x+1}{x^2−1}$ en el intervalo$ [2,4]$

31) [T]$L_{100}$ y$R_{100}$ para$y=x^3$ en el intervalo$[−1,1]$

Contestar

$alt$

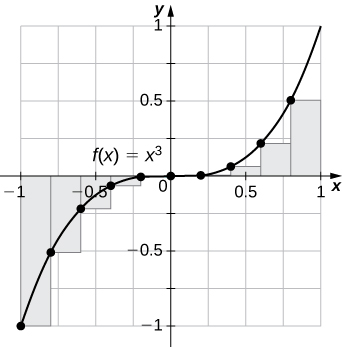
$L_{100}=−0.02,\quad R_{100}=0.02$.
La suma del punto final izquierdo es una subestimación porque la función está aumentando. De manera similar, una aproximación de punto final derecho es una sobreestimación. El área se encuentra entre las estimaciones del punto final izquierdo y derecho.

32) [T]$L_{50}$ y$R_{50}$ para$y=\tan(x)$ en el intervalo$[0,\frac{π}{4}]$

33) [T]$L_{100}$ y$R_{100}$ para$y=e^{2x}$ en el intervalo$[−1,1]$

Contestar

$alt$

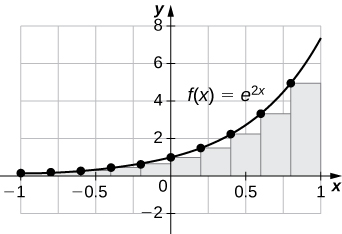
$L_{100}=3.555,\quad R_{100}=3.670$.
La trama muestra que la suma de Riemann izquierda es una subestimación porque la función va en aumento. Se muestran diez rectángulos para mayor claridad visual. Este comportamiento persiste para más rectángulos.

34) Que$t_j$ denote el tiempo que le tomó a Tejay van Garteren montar el$j^\text{th}$ escenario del Tour de Francia en 2014. Si hubo un total de 21 etapas, interprete$\displaystyle \sum_{j=1}^{21}t_j$.

35) Dejar$r_j$ denotar la precipitación total en Portland el$j^\text{th}$ día del año en 2009. Interpretar$\displaystyle \sum_{j=1}^{31}r_j$.

Contestar: La suma representa la precipitación acumulada en enero de 2009.

36) Dejar$d_j$ denotar las horas de luz y$ δ_j$ denotar el incremento de las horas de luz diurna de día$ j−1$ a día$j$ en Fargo, Dakota del Norte, el$j^\text{th}$ día del año. Interpretar$\displaystyle d1+\sum_{j=2}^{365}δ_j.$

37) Para ayudar a ponerse en forma, Joe consigue un nuevo par de zapatillas para correr. Si Joe corre 1 mi cada día en la semana 1 y agrega$\dfrac{1}{10}$ mi a su rutina diaria cada semana, ¿cuál es el kilometraje total en los zapatos de Joe después de 25 semanas?

Contestar: El kilometraje total es$\displaystyle 7×\sum_{i=1}^{25}(1+\frac{(i−1)}{10})=7×25+\frac{7}{10}×12×25=385$ mi.

38) El siguiente cuadro da valores aproximados de la tasa atmosférica promedio anual de incremento del dióxido de carbono (CO ₂) cada década desde 1960, en partes por millón (ppm). Estimar el incremento total del CO ₂ atmosférico entre 1964 y 2013.

Década	PPM/y
1964-1973	1.07
1976-1983	1.34
1984-1993	1.40
1994-2003	1.87
2004-2013	2.07

Incremento anual promedio de CO2 atmosférico, 1964—2013 Fuente: http://www.esrl.noaa.gov/gmd/ccgg/trends/.

39) La siguiente tabla da el incremento aproximado del nivel del mar en pulgadas a lo largo de 20 años a partir del año dado. Estimar el cambio neto en el nivel medio del mar de 1870 a 2010.

Año Inicial	Cambio de 20 años
1870	0.3
1890	1.5
1910	0.2
1930	2.8
1950	0.7
1970	1.1
1990	1.5

Incrementos aproximados del nivel del mar a 20 años, 1870—1990

Origen: http://link.springer.com/article/10....712-011-9119-1

Contestar: Suma los números para obtener 8.1-in. incremento neto.

40) El siguiente cuadro da el incremento aproximado en dólares en el precio promedio de un galón de gas por década desde 1950. Si el precio promedio de un galón de gas en 2010 fue de $2.60, ¿cuál fue el precio promedio de un galón de gas en 1950?

Año Inicial	Cambio de 10 años
1950	0.03
1960	0.05
1970	0.86
1980	−0.03
1990	0.29
2000	1.12

Incrementos aproximados en el precio del gas a 10 años, 1950—2000

Fuente: epb.lbl.gov/homepages/rick_di... 011-trends.pdf.

41) La siguiente tabla da el porcentaje de crecimiento de la población estadunidense a partir de julio del año indicado. Si la población de Estados Unidos era de 281,421,906 en julio de 2000, estime la población estadounidense en julio de 2010.

Año	% cambio/año
2000	1.12
2001	0.99
2002	0.93
2003	0.86
2004	0.93
2005	0.93
2006	0.97
2007	0.96
2008	0.95
2009	0.88

Crecimiento porcentual anual de la población de Estados Unidos, 2000—2009

Fuente: www.census.gov/popest/data.

(Pista: Para obtener la población en julio de 2001, multiplicar la población en julio de 2000 por 1.0112 para obtener 284,573,831.)

Contestar: 309,389,957

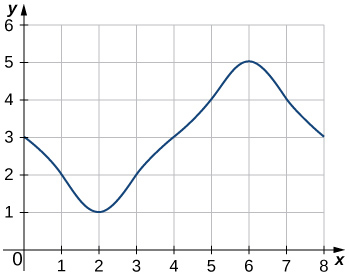
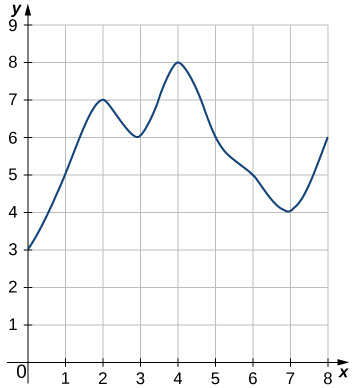
En los ejercicios 42 - 45, estimar las áreas bajo las curvas calculando las sumas de Riemann izquierdas,$L_8.$

42)

$alt$

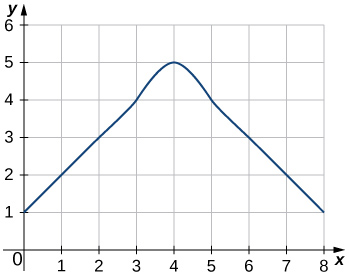
43)

$alt$

Contestar: $L_8=3+2+1+2+3+4+5+4=24$

44)

$alt$

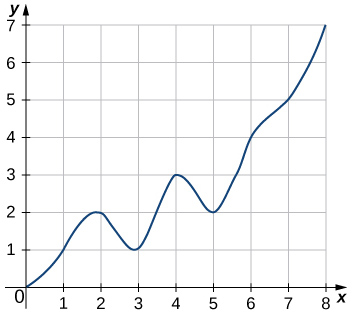
45)

$alt$

Contestar: $L_8=3+5+7+6+8+6+5+4=44$

46) [T] Usar un sistema de álgebra computacional para calcular la suma de Riemann$ L_N$,,$ N=10,30,50$ for$ f(x)=\sqrt{1−x^2}$ on$[−1,1].$

47) [T] Utilizar un sistema de álgebra computacional para calcular la suma de Riemann$L_N$,,$N=10,30,50$ for$f(x)=\dfrac{1}{\sqrt{1+x^2}}$ on$[−1,1].$

Contestar: $L_{10}≈1.7604,\quad L_{30}≈1.7625,\quad L_{50}≈1.76265$

48) [T] Utilizar un sistema de álgebra computacional para calcular la suma de Riemann$L_N$,,$N=10,30,50$ for$f(x)=\sin^2 x$ on$ [0,2π]$. Comparar estas estimaciones con$π$.

En los ejercicios 49-50, utilice una calculadora o un programa de computadora para evaluar las sumas de punto final$R_N$ y$L_N$ para$N=1,10,100$. ¿Cómo se comparan estas estimaciones con las respuestas exactas, que puedes encontrar a través de la geometría?

49) [T]$y=\cos(πx)$ en el intervalo$[0,1]$

Contestar: $R_1=−1,\quad L_1=1,$
$R_{10}=−0.1,\quad L_{10}=0.1,$
$L_{100}=0.01,\quad R_{100}=−0.01.$
Por simetría de la gráfica, el área exacta es cero.

50) [T]$y=3x+2$ en el intervalo$[3,5]$

En los ejercicios 51 - 52, utilice una calculadora o un programa de computadora para evaluar las sumas de punto final$R_N$ y$L_N$ para$N=1,10,100.$

51) [T]$y=x^4−5x^2+4$ en el intervalo$[−2,2]$, que tiene un área exacta de$\frac{32}{15}$

Contestar: $R_1=0,\quad L_1=0,$
$R_{10}=2.4499,\quad L_{10}=2.4499,$
$R_{100}=2.1365,\quad L_{100}=2.1365$

52) [T]$y=\ln x$ en el intervalo$[1,2]$, que tiene un área exacta de$2\ln(2)−1$

53) Explicar por qué, si$f(a)≥0$ y$f$ va aumentando en$[a,b]$, que la estimación del punto final izquierdo es un límite inferior para el área debajo de la gráfica de$f$ on$ [a,b].$

Contestar: Si$[c,d]$ es un subintervalo de$ [a,b]$ debajo de uno de los rectángulos de suma del extremo izquierdo, entonces el área del rectángulo que contribuye a la estimación del punto final izquierdo es$ f(c)(d−c)$. Pero,$f(c)≤f(x)$ para$c≤x≤d$, así el área bajo la gráfica de$f$ entre$c$ y$d$ es$f(c)(d−c)$ más el área debajo de la gráfica de$f$ pero por encima del segmento de línea horizontal a la altura$f(c)$, lo cual es positivo. Como esto es cierto para cada intervalo de suma de extremo izquierdo, se deduce que la suma de Riemann izquierda es menor o igual que el área debajo de la gráfica de$f$ on$[a,b].$

54) Explicar por qué, si$f(b)≥0$ y f es decreciente sobre$ [a,b],$ eso la estimación del punto final izquierdo es un límite superior para el área debajo de la gráfica de$f$ on$ [a,b].$

55) Demostrar que, en general,$ R_N−L_N=(b−a)×\dfrac{f(b)−f(a)}{N}.$

Contestar: $\displaystyle L_N=\frac{b−a}{N}\sum_{i=1}^Nf(a+(b−a)\frac{i−1}{N})=\frac{b−a}{N}\sum_{i=0}^{N−1}f(a+(b−a)\frac{i}{N})$y$\displaystyle R_N=\frac{b−a}{N}\sum_{i=1}^Nf(a+(b−a)\frac{i}{N})$. La suma izquierda tiene un término correspondiente a$i=0$ y la suma derecha tiene un término correspondiente a$i=N$. En$R_N−L_N$, cualquier término correspondiente a$i=1,2,…,N−1$ ocurre una vez con un signo más y una vez con un signo menos, por lo que cada término se cancela y uno se queda con$R_N−L_N=\dfrac{b−a}{N}(f(a+(b−a))\dfrac{N}{N})−(f(a)+(b−a)\dfrac{0}{N})=\dfrac{b−a}{N}(f(b)−f(a)).$

56) Explique por qué, si$f$ va aumentando en$[a,b]$, el error entre cualquiera$L_N$ o$R_N$ y el área$A$ debajo de la gráfica de$f$ es como máximo$(b−a)\dfrac{f(b)−f(a)}{N}$.

57) Para cada una de las tres gráficas:

a. Obtener un límite inferior$L(A)$ para el área encerrada por la curva sumando las áreas de los cuadrados encerradas completamente por la curva.

b. Obtener un límite superior$U(A)$ para el área sumando a$L(A)$ las áreas$B(A)$ de los cuadrados encerrados parcialmente por la curva.

$alt$

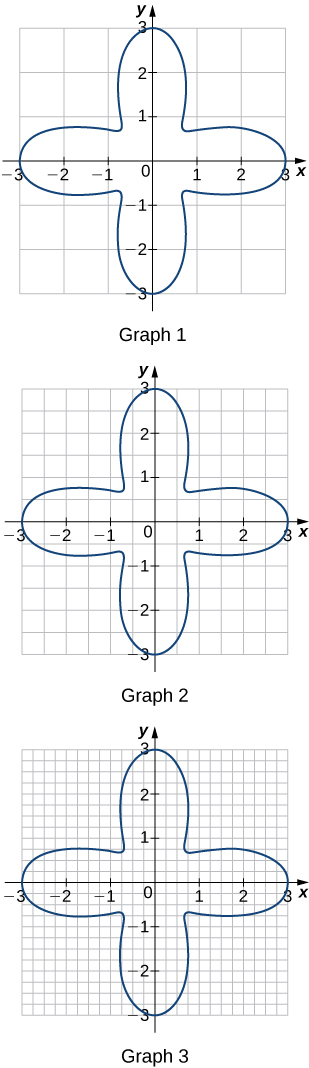
Contestar: Gráfica 1: a.$L(A)=0,\quad B(A)=20; \quad b. U(A)=20.$
Gráfica 2:$a. L(A)=9; \quad b. B(A)=11,\quad U(A)=20.$
Gráfica 3: a.$ L(A)=11.0; \quad b. B(A)=4.5,\quad U(A)=15.5.$

58) En el ejercicio anterior, explique por qué no$ L(A)$ se hace menor mientras que no$U(A)$ se hace más grande ya que los cuadrados se subdividen en cuatro casillas de igual área.

59) Un círculo unitario se compone de n cuñas equivalentes a la cuña interna en la figura. La base del triángulo interior es de 1 unidad y su altura es$\sin(\frac{π}{n}).$ La base del triángulo exterior es$B=\cos(\frac{π}{n})+\sin(\frac{π}{n})\tan(\frac{π}{n})$ y la altura es$H=B\sin(\frac{2π}{n})$. Utilice esta información para argumentar que el área de un círculo unitario es igual a$π.$

$alt$

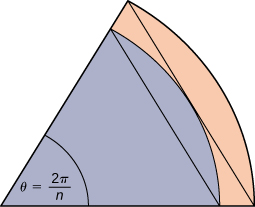
Contestar: Dejar$A$ ser el área del círculo de la unidad. El círculo encierra triángulos$n$ congruentes cada uno de área$\dfrac{\sin(\dfrac{2π}{n})}{2}$, así de$\frac{n}{2}\sin(\frac{2π}{n})≤A.$ manera similar, el círculo está contenido dentro de triángulos$n$ congruentes cada uno de área$\dfrac{BH}{2}=\frac{1}{2}(\cos(\frac{π}{n})+\sin(\frac{π}{n})\tan(\frac{π}{n}))\sin(\frac{2π}{n})$, entonces$ A≤\frac{n}{2}\sin(\frac{2π}{n})(\cos(\frac{π}{n}))+\sin(\frac{π}{n})\tan(\frac{π}{n})$. Como$n→∞,\quad \frac{n}{2}\sin(\frac{2π}{n})=\frac{π\sin(\frac{2π}{n})}{(\frac{2π}{n})}→π$, así concluimos$π≤A$. También, como$ n→∞,\quad \cos(\frac{π}{n})+\sin(\frac{π}{n})\tan(\frac{π}{n})→1$, así también tenemos$A≤π$. Por el teorema de squeeze para los límites, concluimos que$A=π.$