5.4E: Ejercicios para la Sección 5.4
- Page ID
- 116225
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En los ejercicios 1 - 6, utilice fórmulas básicas de integración para computar las siguientes antiderivadas.
1)\(\displaystyle ∫\left(\sqrt{x}−\frac{1}{\sqrt{x}}\right)\,dx\)
- Contestar
- \(\displaystyle ∫\left(\sqrt{x}−\frac{1}{\sqrt{x}}\right)\,dx=∫x^{1/2}\,dx−∫x^{−1/2}\,dx=\frac{2}{3}x^{3/2}+C_1−2x^{1/2+}C_2=\frac{2}{3}x^{3/2}−2x^{1/2}+C\)
2)\(\displaystyle ∫\left(e^{2x}−\frac{1}{2}e^{x/2}\right)\,dx\)
3)\(\displaystyle ∫\frac{dx}{2x}\)
- Contestar
- \(\displaystyle ∫\frac{dx}{2x}=\frac{1}{2}\ln|x|+C\)
4)\(\displaystyle ∫\frac{x−1}{x^2}\,dx\)
5)\(\displaystyle ∫^π_0(\sin x−\cos x)\,dx\)
- Contestar
- \(\displaystyle ∫^π_0\sin x\,dx−∫^π_0\cos x\,dx=−\cos x\big|^π_0−(\sin x)\big|^π_0=(−(−1)+1)−(0−0)=2\)
6)\(\displaystyle ∫^{π/2}_0(x−\sin x)\,dx\)
7) Escribir una integral que exprese el incremento en el perímetro\(P(s)\) de un cuadrado cuando su longitud lateral\(s\) aumente de 2 unidades a 4 unidades y evalúe la integral.
- Contestar
- \(P(s)=4s,\)así\(\dfrac{dP}{ds}=4\) y\(\displaystyle ∫^4_24\,ds=8.\)
8) Escribir una integral que cuantifique el cambio en el área\(A(s)=s^2\) de un cuadrado cuando la longitud lateral se duplica de\(S\) unidades a\(2S\) unidades y evalúe la integral.
9) Un\(N\) -gon regular (un\(N\) polígono de lados con lados que tienen igual longitud\(s\), como un pentágono o hexágono) tiene perímetro\(Ns.\) Escribe una integral que exprese el incremento en el perímetro de un\(N\) -gon regular cuando la longitud de cada lado aumenta de 1 unidad a 2 unidades y evaluar la integral.
- Contestar
- \(\displaystyle ∫^2_1N\,ds=N\)
10) El área de un pentágono regular con longitud lateral\(a>0\) es\(pa^2\) con\(p=\frac{1}{4}\sqrt{5+\sqrt{5+2\sqrt{5}}}\). El Pentágono en Washington, DC, tiene lados interiores de longitud 360 pies y lados exteriores de longitud 920 pies. Escribir una integral para expresar el área de la cubierta del Pentágono de acuerdo a estas dimensiones y evaluar esta área.
11) Un dodecaedro es un sólido platónico con una superficie que consta de 12 pentágonos, cada uno de igual área. ¿En cuánto aumenta la superficie de un dodecaedro a medida que la longitud lateral de cada pentágono se duplica de 1 unidad a 2 unidades?
- Contestar
- Con\(p\) como en el ejercicio anterior, cada uno de los 12 pentágonos aumenta en área de\(2p\) a\(4p\) unidades por lo que el incremento neto en el área del dodecaedro es\(36p\) unidades.
12) Un icosaedro es un sólido platónico con una superficie que consta de 20 triángulos equiláteros. ¿En cuánto aumenta la superficie de un icosaedro a medida que la longitud lateral de cada triángulo se duplica de una unidad a\(2a\) unidades?
13) Escribir una integral que cuantifique el cambio en el área de la superficie de un cubo cuando su longitud lateral se duplique de\(s\) unidad a\(2s\) unidades y evalúe la integral.
- Contestar
- \(\displaystyle 18s^2=6∫^{2s}_s 2x\,dx\)
14) Escribir una integral que cuantifique el incremento en el volumen de un cubo cuando la longitud lateral se duplica de\(s\) unidad a\(2s\) unidades y evalúe la integral.
15) Escribir una integral que cuantifique el incremento en la superficie de una esfera a medida que su radio se duplica de\(R\) unidad a\(2R\) unidades y evalúe la integral.
- Contestar
- \(\displaystyle 12πR^2=8π∫^{2R}_Rr\,dr\)
16) Escribir una integral que cuantifique el incremento en el volumen de una esfera a medida que su radio se duplica de\(R\) unidad a\(2R\) unidades y evalúe la integral.
17) Supongamos que una partícula se mueve a lo largo de una línea recta con velocidad\(v(t)=4−2t,\) donde\(0≤t≤2\) (en metros por segundo). Encuentra el desplazamiento en el momento\(t\) y la distancia total recorrida hasta\(t=2.\)
- Contestar
- \(\displaystyle d(t)=∫^t_0v(s)\,ds=4t−t^2.\)La distancia total es\(d(2)=4\) m.
18) Supongamos que una partícula se mueve a lo largo de una línea recta con la velocidad definida por\(v(t)=t^2−3t−18,\) donde\(0≤t≤6\) (en metros por segundo). Encuentra el desplazamiento en el momento\(t\) y la distancia total recorrida hasta\(t=6.\)
19) Supongamos que una partícula se mueve a lo largo de una línea recta con la velocidad definida por\(v(t)=|2t−6|,\) donde\(0≤t≤6\) (en metros por segundo). Encuentra el desplazamiento en el momento\(t\) y la distancia total recorrida hasta\(t=6.\)
- Contestar
- \(\displaystyle d(t)=∫^t_0v(s)\,ds.\)Para\(t<3,\;d(t)=∫^t_0(6−2t)\,dt=6t−t^2.\) Para\(\displaystyle t>3,\;d(t)=d(3)+∫^t_3(2t−6)\,dt=9+(t^2−6t).\) La distancia total es\(d(6)=9\) m.
20) Supongamos que una partícula se mueve a lo largo de una línea recta con aceleración definida por\(a(t)=t−3,\) donde\(\displaystyle 0≤t≤6\) (en metros por segundo). Encuentre la velocidad y el desplazamiento en el tiempo\(t\) y la distancia total recorrida hasta\(t=6\) si\(v(0)=3\) y\( d(0)=0.\)
21) Se lanza una pelota hacia arriba desde una altura de 1.5 m a una velocidad inicial de 40 m/seg. La aceleración resultante de la gravedad\(−9.8\, \text{m/sec}^2.\) es Descuidar la resistencia del aire, resolver por la velocidad\(v(t)\) y la altura\(h(t)\) de la pelota\(t\) segundos después de que sea lanzada y antes de que regrese al suelo.
- Contestar
- \(v(t)=40−9.8t;\; h(t)=1.5+40t−4.9t^2\)m/s
22) Se lanza una pelota hacia arriba desde una altura de 3 m a una velocidad inicial de 60 m/seg. La aceleración resultante de la gravedad es\(−9.8 \, \text{m/sec}^2\). Despreciando la resistencia del aire, resuelva por la velocidad\(v(t)\) y la altura\(h(t)\) de la pelota\(t\) segundos después de que sea lanzada y antes de que regrese al suelo.
23) El área\(A(t)\) de forma circular está creciendo a un ritmo constante. Si el área aumenta de\(4π\) unidades a\(9π\) unidades entre tiempos\(t=2\) y\(t=3,\) encuentra el cambio neto en el radio durante ese tiempo.
- Contestar
- El incremento neto es de 1 unidad.
24) Un globo esférico está siendo inflado a una velocidad constante. Si el volumen del globo cambia de\(36π \text{ in}^3\) a\(288π \text{ in}^3\) entre tiempo\(t=30\) y\(t=60\) segundos, encuentre el cambio neto en el radio del globo durante ese tiempo.
25) El agua fluye hacia un tanque cónico con área de sección transversal\(πx^2\) a altura\(x\) y volumen\(\frac{πx^3}{3}\) hasta altura\(x.\) Si el agua fluye hacia el tanque a una velocidad de 1\(\text{m}^3\text{/min},\) encontrar la altura del agua en el tanque después de 5 min. Encuentra el cambio de altura entre 5 min y 10 min.
- Contestar
- A\(t=5\), la altura del agua es\(x=\left(\frac{15}{π}\right)^{1/3}\) m. El cambio neto en altura de\(t=5\) a\(t=10\) es\(\left(\left(\frac{30}{π}\right)^{1/3}−\left(\frac{15}{π}\right)^{1/3}\right)\) m.
26) Un tanque cilíndrico horizontal tiene área de sección transversal\(A(x)=4(6x−x^2)\,\text{m}^2\) a\(x\) metros de altura por encima del fondo cuando\(x≤3.\)
a. el volumen\(V\) entre alturas\(a\) y\(b\) es\(\displaystyle ∫^b_aA(x)\,dx.\) Encontrar el volumen en alturas entre 2 m y 3 m.
b. Supongamos que el petróleo se está bombeando al tanque a una velocidad de 50 L/min. Usando la regla de la cadena, ¿\(\dfrac{dx}{dt}=\dfrac{dx}{dV}\dfrac{dV}{dt},\)a cuántos metros por minuto está cambiando la altura del petróleo en el tanque, expresada en términos de\(x,\) cuándo la altura está en\(x\) metros?
c. ¿Cuánto tiempo se tarda en llenar el tanque a 3 m a partir de un nivel de llenado de 2 m?
27) La siguiente tabla enumera la energía eléctrica en gigavatios —la tasa a la que se consuma la energía— utilizada en una ciudad determinada para diferentes horas del día, en un periodo típico de 24 horas, con la hora 1 correspondiente a la medianoche a la 1 de la mañana.
| Hora | Poder | Hora | Poder |
| 1 | 28 | 13 | 48 |
| 2 | 25 | 14 | 49 |
| 3 | 24 | 15 | 49 |
| 4 | 23 | 16 | 50 |
| 5 | 24 | 17 | 50 |
| 6 | 27 | 18 | 50 |
| 7 | 29 | 19 | 46 |
| 8 | 32 | 20 | 43 |
| 9 | 34 | 21 | 42 |
| 10 | 39 | 22 | 40 |
| 11 | 42 | 23 | 37 |
| 12 | 46 | 24 | 34 |
Encuentra la cantidad total de energía en gigavatios-hora (Gw-h) consumida por la ciudad en un periodo típico de 24 horas.
- Contestar
- El consumo total diario de energía se estima como la suma de las tarifas de energía por hora, o 911 GW-h.
28) El uso promedio de energía eléctrica residencial (en cientos de vatios) por hora se da en la siguiente tabla.
| Hora | Poder | Hora | Poder |
| 1 | 8 | 13 | 12 |
| 2 | 6 | 14 | 13 |
| 3 | 5 | 15 | 14 |
| 4 | 4 | 16 | 15 |
| 5 | 5 | 17 | 17 |
| 6 | 6 | 18 | 19 |
| 7 | 7 | 19 | 18 |
| 8 | 8 | 20 | 17 |
| 9 | 9 | 21 | 16 |
| 10 | 10 | 22 | 16 |
| 11 | 10 | 23 | 13 |
| 12 | 11 | 24 | 11 |
a. Calcular la energía total promedio utilizada en un día en kilovatios-hora (kWh).
b. Si una tonelada de carbón genera 1842 kWh, ¿cuánto tiempo tarda una residencia promedio en quemar una tonelada de carbón?
c. Explicar por qué los datos podrían ajustarse a una gráfica del formulario\(p(t)=11.5−7.5\sin\left(\frac{πt}{12}\right).\)
29) Los datos de la siguiente tabla se utilizan para estimar la potencia promedio producida por Peter Sagan para cada uno de los últimos 18 segundos de la Etapa 1 del Tour de Francia 2012.
| Segundo | Watts | Segundo | Watts |
| 1 | 600 | 10 | 1200 |
| 2 | 500 | 11 | 1170 |
| 3 | 575 | 12 | 1125 |
| 4 | 1050 | 13 | 1100 |
| 5 | 925 | 14 | 1075 |
| 6 | 950 | 15 | 1000 |
| 7 | 1050 | 16 | 950 |
| 8 | 950 | 17 | 900 |
| 9 | 1100 | 18 | 780 |
Salida de energía promedio Fuente: sportsexercisengineering.com
Estimar la energía neta utilizada en kilojulios (kJ), señalando que 1W = 1 J/s, y la potencia promedio de salida por Sagan durante este intervalo de tiempo.
- Contestar
- \(17\)kJ
30) Los datos de la siguiente tabla se utilizan para estimar la potencia promedio producida por Peter Sagan para cada intervalo de 15 min de la Etapa 1 del Tour de Francia 2012.
| Minutas | Watts | Minutas | Watts |
| 15 | 200 | 165 | 170 |
| 30 | 180 | 180 | 220 |
| 45 | 190 | 195 | 140 |
| 60 | 230 | 210 | 225 |
| 75 | 240 | 225 | 170 |
| 90 | 210 | 240 | 10 |
| 105 | 210 | 255 | 200 |
| 1120 | 220 | 270 | 220 |
| 135 | 210 | 285 | 250 |
| 150 | 150 | 300 | 400 |
Fuente de salida de potencia promedio: sportsexercisengineering.com
Estimar la energía neta utilizada en kilojulios, señalando que 1W = 1 J/s.
31) La distribución de los ingresos a partir de 2012 en Estados Unidos en incrementos de 5000 dólares se da en la siguiente tabla. La fila késima denota el porcentaje de hogares con ingresos entre\($5000xk\) y\(5000xk+4999\). La fila\(k=40\) contiene todos los hogares con ingresos entre $200,000 y $250.000 y\(k=41\) cuentas para todos los hogares con ingresos superiores a $250,000.
| 0 | 3.5 | 21 | 1.5 |
| 1 | 4.1 | 22 | 1.4 |
| 2 | 5.9 | 23 | 1.3 |
| 3 | 5.7 | 24 | 1.3 |
| 4 | 5.9 | 25 | 1.1 |
| 5 | 5.4 | 26 | 1.0 |
| 6 | 5.5 | 27 | 0.75 |
| 7 | 5.1 | 28 | 0.8 |
| 8 | 4.8 | 29 | 1.0 |
| 9 | 4.1 | 30 | 0.6 |
| 10 | 4.3 | 31 | 0.6 |
| 11 | 3.5 | 32 | .5 |
| 12 | 3.7 | 33 | 0.5 |
| 13 | 3.2 | 34 | 0.4 |
| 14 | 3.0 | 35 | 0.3 |
| 15 | 2.8 | 36 | 0.3 |
| 16 | 2.5 | 37 | 0.3 |
| 17 | 2.2 | 38 | 0.2 |
| 18 | 2.2 | 39 | 1.8 |
| 19 | 1.8 | 40 | 2.3 |
| 20 | 2.1 | 41 |
Distribuciones de ingresosFuente: http://www.census.gov/prod/2013pubs/p60-245.pdf
a. Estimar el porcentaje de hogares estadounidenses en 2012 con ingresos inferiores a 55,000 dólares.
b. ¿Qué porcentaje de hogares tenían ingresos superiores a 85,000 dólares?
c. Trazar los datos y tratar de ajustar su forma a la de una gráfica de la forma\(a(x+c)e^{−b(x+e)}\) para adecuada\(a,\, b,\, c.\)
- Contestar
-
a. 54.3%;
b. 27.00%;
c. La curva en la siguiente parcela es\(2.35(t+3)e^{−0.15(t+3)}.\)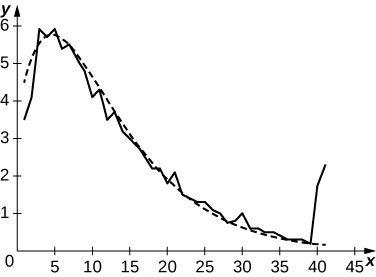
32) La ley de gravedad de Newton establece que la fuerza gravitacional ejercida por un objeto de masa\(M\) y uno de masa\(m\) con centros que están separados por una distancia r es\(F=G\dfrac{mM}{r^2}\), con\(G\) una constante empírica\(G=6.67x10^{−11}\,\text{m}^3/(\text{kg⋅s}^2)\). El trabajo realizado por una fuerza variable a lo largo de un intervalo\( [a,b]\) se define como\(\displaystyle W=∫^b_aF(x)\,dx\). Si la Tierra tiene masa\(5.97219×10^{24}\) y radio 6371 km, calcule la cantidad de trabajo para elevar un satélite meteorológico polar de masa 1400 kg a su altitud orbitante de 850 km sobre la Tierra.
33) Para un vehículo de motor determinado, la desaceleración máxima alcanzable del frenado es aproximadamente\(7 \text{ m/sec}^2\) sobre concreto seco. Sobre asfalto mojado, es aproximadamente\(2.5 \text{ m/sec}^2.\) Dado que 1 mph corresponde a 0.447 m/seg, encuentra la distancia total que recorre un automóvil en metros sobre concreto seco después de aplicar los frenos hasta que se detenga por completo si la velocidad inicial es de 67 mph (30 m/seg) o si la velocidad inicial de frenado es de 56 mph (25 m/seg). Encuentra las distancias correspondientes si la superficie es de asfalto húmedo resbaladizo.
- Contestar
- En condiciones secas, con velocidad inicial\(v_0=30\) m/s,\(D=64.3\) y, si\(v_0=25,\; D=44.64\). En condiciones húmedas, si\(v_0=30\),\(D=180\) y si\(v_0=25,\;D=125.\)
34) John es un hombre de 25 años que pesa 160 lb. quema\(500−50t\) calorías/hr mientras montaba su bicicleta durante\(t\) horas. Si una galleta de avena tiene 55 cal y John come\(4t\) galletas durante la\(t^{\text{th}}\) hora, ¿cuántas calorías netas ha perdido después de 3 horas montando su bicicleta?
35) Sandra es una mujer de 25 años que pesa 120 lbs. quema\(300−50t\) cal/hr mientras camina sobre su cinta de correr durante\(t\) horas. Su ingesta calórica por beber Gatorade es\(100t\) calorías durante la\(t^{\text{th}}\) hora. ¿Cuál es su disminución neta de calorías después de caminar durante 3 horas?
- Contestar
- 225 cal
36) Un vehículo de motor tiene una eficiencia máxima de 33 mpg a una velocidad de crucero de 40 mph. La eficiencia disminuye a una velocidad de 0.1 mpg/mph entre 40 mph y 50 mph, y a una velocidad de 0.4 mpg/mph entre 50 mph y 80 mph. ¿Cuál es la eficiencia en millas por galón si el auto está en crucero a 50 mph? ¿Cuál es la eficiencia en millas por galón si el auto está en crucero a 80 mph? Si la gasolina cuesta $3.50/gal, ¿cuál es el costo del combustible para conducir 50 km a 40 mph, a 50 mph y a 80 mph?
37) Aunque algunos motores son más eficientes a una potencia dada que otros, en promedio, la eficiencia del combustible disminuye con los caballos de fuerza a una tasa de\(1/25\) mpg/caballos de fuerza. Si un motor típico de 50 caballos de fuerza tiene una eficiencia promedio de combustible de 32 mpg, ¿cuál es la eficiencia promedio de combustible de un motor con los siguientes caballos de fuerza: 150, 300, 450?
- Contestar
- \( E(150)=28,\;E(300)=22,\;E(450)=16\)
38) [T] La siguiente tabla enumera el cronograma 2013 del impuesto federal sobre la renta versus ingresos imponibles.
| Rango de Ingresos Imponibles | El Impuesto Es... | ... De la cantidad superior |
| $0—$8925 | 10% | $0 |
| $8925—$36,250 | $892.50 + 15% | $8925 |
| $36,250—$87,850 | $4,991.25 + 25% | $36,250 |
| $87,850—$183,250 | $17,891.25 + 28% | $87,850 |
| $183,250—$398,350 | $44,603.25 + 33% | $183,250 |
| $398,350—$400,000 | $115,586.25 + 35% | $398,350 |
| > $400,000 | $116,163.75 + 39.6% | $400,000 |
Impuesto federal sobre la renta versus ingresos imponibles Fuente: http://www.irs.gov/pub/irs-prior/i1040tt--2013.pdf.
Supongamos que Steve acaba de recibir un aumento de 10.000 dólares. ¿Cuánto de este aumento queda después de los impuestos federales si el salario de Steve antes de recibir el aumento era de 40,000 dólares? ¿Si eran 90.000 dólares? ¿Si era 385.000 dólares?
39) [T] La siguiente tabla proporciona datos hipotéticos con respecto al nivel de servicio para una determinada autopista.
| Rango de velocidad en carretera (mph) | Vehículos por Hora por Carril | Rango de Densidad (vehículos/mi) |
| >60 | <600 | <10 |
| 60-57 | 300-1000 | 10-20 |
| 57-54 | 1000-1500 | 20-30 |
| 57-54 | 1500-1900 | 30-45 |
| 46-30 | 1900-2100 | 48-70 |
| <30 | Inestable | 70-200 |
a. Trazar vehículos por hora por carril en el\(x\) eje y velocidad de la carretera en el\(y\) eje.
b. Calcular la disminución promedio de velocidad (en millas por hora) por unidad de incremento en la congestión (vehículos por hora por carril) ya que esta última aumenta de 600 a 1000, de 1000 a 1500, y de 1500 a 2100. ¿La disminución en millas por hora depende linealmente del incremento de vehículos por hora por carril?
c. Trazar minutos por milla (60 veces el recíproco de millas por hora) en función de vehículos por hora por carril. ¿Esta función es lineal?
- Contestar
-
a.
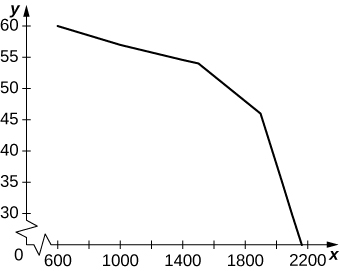
b. entre 600 y 1000 la disminución promedio de vehículos por hora por carril es de −0.0075. Entre 1000 y 1500 es −0.006 por vehículos por hora por carril, y entre 1500 y 2100 es −0.04 vehículos por hora por carril.
c.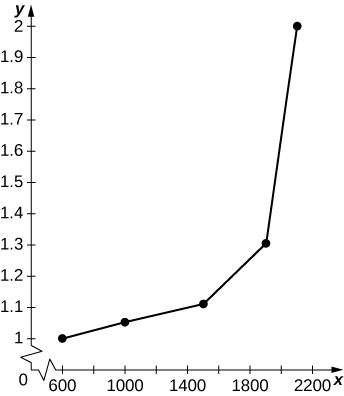
El gráfico es no lineal, con minutos por milla aumentando drásticamente a medida que los vehículos por hora por carril alcanzan 2000.
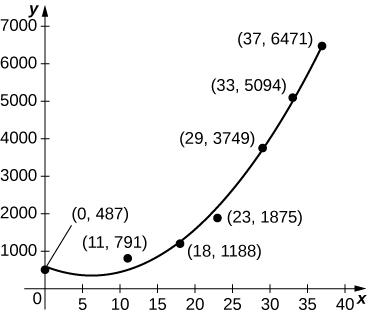
Para los dos ejercicios siguientes utilice los datos de la siguiente tabla, que muestra poblaciones de águila calva de 1963 a 2000 en los Estados Unidos continentales.
| Año | Población de parejas reproductoras de águilas calvas |
| 1963 | 487 |
| 1974 | 791 |
| 1981 | 1188 |
| 1986 | 1875 |
| 1992 | 3749 |
| 1996 | 5094 |
| 2000 | 6471 |
Población de Pares de Águila Calva Cría Fuente: http://www.fws.gov/Midwest/eagle/pop... /chtofprs.html.
40) [T] La gráfica siguiente traza la cuadrática\(p(t)=6.48t^2−80.31t+585.69\) frente a los datos de la tabla anterior, normalizada de manera que\(t=0\) corresponde a 1963. Estimar el número promedio de águilas calvas por año presentes para los 37 años calculando el valor promedio de\(p\) más\([0,37].\)
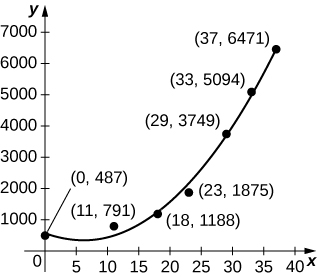
41) [T] La gráfica siguiente traza el cúbico\(p(t)=0.07t^3+2.42t^2−25.63t+521.23\) frente a los datos de la tabla anterior, normalizado de manera que\(t=0\) corresponde a 1963. Estimar el número promedio de águilas calvas por año presentes para los 37 años calculando el valor promedio de\(p\) más\([0,37].\)
- Contestar
- \(\displaystyle \frac{1}{37}∫^{37}_0p(t)\,dt=\frac{0.07(37)^3}{4}+\frac{2.42(37)^2}{3}−\frac{25.63(37)}{2}+521.23≈2037\)
Solución:
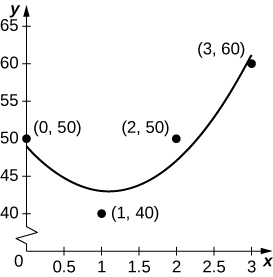
42) [T] Supongamos que va de viaje por carretera y registra su velocidad cada media hora, tal y como se recoge en la siguiente tabla. El mejor ajuste cuadrático a los datos es\(q(t)=5x^2−11x+49\), que se muestra en la gráfica que lo acompaña. Integrar\(q\) para estimar la distancia total recorrida a lo largo de las 3 horas.
| Tiempo (hr) | Velocidad (m [h) |
| 0 (inicio) | 50 |
| 1 | 40 |
| 2 | 50 |
| 3 | 60 |
A medida que un automóvil acelera, no acelera a un ritmo constante; más bien, la aceleración es variable. Para los siguientes ejercicios, utilice la siguiente tabla, que contiene la aceleración medida a cada segundo a medida que un conductor se fusiona con una autopista.
| Tiempo (seg) | Aceleración (mph/seg) |
| 1 | 11.2 |
| 2 | 10.6 |
| 3 | 8.1 |
| 4 | 5.4 |
| 5 | 0 |
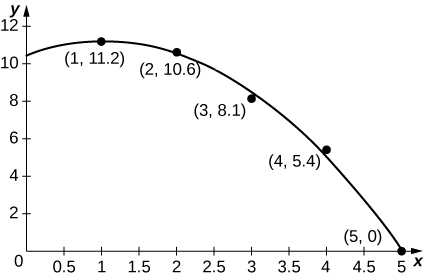
43) [T] La gráfica adjunta traza el mejor ajuste cuadrático,\(a(t)=−0.70t^2+1.44t+10.44\), a los datos de la tabla anterior. Calcular el valor promedio de\(a(t)\) para estimar la aceleración promedio entre\(t=0\) y\(t=5.\)
- Contestar
- La aceleración promedio es\(\displaystyle A=\frac{1}{5}∫^5_0a(t)\,dt=−\frac{0.7(5^2)}{3}+\frac{1.44(5)}{2}+10.44≈8.2\) mph/s
44) [T] Usando tu ecuación de aceleración del ejercicio anterior, encuentra la ecuación de velocidad correspondiente. Suponiendo que la velocidad final es de 0 mph, encuentre la velocidad en el momento\(t=0.\)
45) [T] Usando tu ecuación de velocidad del ejercicio anterior, encuentra la ecuación de distancia correspondiente, asumiendo que tu distancia inicial es de 0 mi. ¿Hasta dónde viajaste mientras acelerabas tu auto? (Sugerencia: Necesitarás convertir unidades de tiempo).
- Contestar
- \(\displaystyle d(t)=∫^1_0|v(t)|\,dt=∫^t_0\left(\frac{7}{30}t^3−0.72t^2−10.44t+41.033\right)\,dt=\frac{7}{120}t^4−0.24t^3−5.22t^3+41.033t.\)Entonces,\(d(5)≈81.12 \,\text{mph} × \text{sec}≈119\) pies.
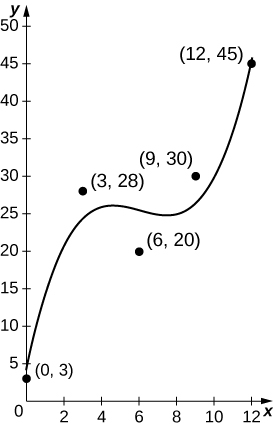
46) [T] El número de hamburguesas vendidas en un restaurante a lo largo del día se da en la siguiente tabla, con la gráfica acompañante trazando el mejor ajuste cúbico a los datos,\(b(t)=0.12t^3−2.13t^3+12.13t+3.91,\) con\(t=0\) correspondiente a las 9 a.m. y\(t=12\) correspondientes a las 9 p.m. Calcular el valor promedio de\(b(t)\) a estimar el promedio de hamburguesas vendidas por hora.
| Horas Pasadas la Medianoche | No. de Hamburguesas vendidas |
| 9 | 3 |
| 12 | 28 |
| 15 | 20 |
| 18 | 30 |
| 21 | 45 |
47) [T] Una atleta corre por un detector de movimiento, que registra su velocidad, como se muestra en la siguiente tabla. El mejor ajuste lineal a estos datos,\(ℓ(t)=−0.068t+5.14\), se muestra en la gráfica que lo acompaña. Utilice el valor promedio de\(ℓ(t)\) entre\(t=0\) y\(t=40\) para estimar la velocidad promedio del corredor.
| Minutas | Velocidad (m/seg) |
| 0 | 5 |
| 10 | 4.8 |
| 20 | 3.6 |
| 30 | 3.0 |
| 40 | 2.5 |
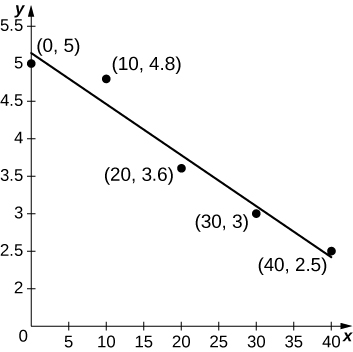
- Contestar
- \(\displaystyle \tfrac{1}{40} ∫^{40}_0(−0.068t+5.14)\,dt=−\frac{0.068(40)}{2}+5.14=3.78\) m/sec