5.6E: Ejercicios para la Sección 5.6

Última actualización
Guardar como PDF

Page ID: 116215

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Para los ejercicios 1 - 8, computar cada integral indefinida.

1)$\displaystyle ∫e^{2x}\,dx$

2)$\displaystyle ∫e^{−3x}\,dx$

Contestar: $\displaystyle ∫e^{−3x}\,dx \quad = \quad \frac{−1}{3}e^{−3x}+C$

3)$\displaystyle ∫2^x\,dx$

4)$\displaystyle ∫3^{−x}\,dx$

Contestar: $\displaystyle ∫3^{−x}\,dx \quad = \quad −\frac{3^{−x}}{\ln 3}+C$

5)$\displaystyle ∫\frac{1}{2x}\,dx$

6)$\displaystyle ∫\frac{2}{x}\,dx$

Contestar: $\displaystyle ∫\frac{2}{x}\,dx \quad = \quad 2\ln x+C \quad = \quad \ln(x^2)+C$

7)$\displaystyle ∫\frac{1}{x^2}\,dx$

8)$\displaystyle ∫\frac{1}{\sqrt{x}}\,dx$

Contestar: $\displaystyle ∫\frac{1}{\sqrt{x}}\,dx \quad = \quad 2\sqrt{x}+C$

En los ejercicios 9 - 16, encuentra cada integral indefinida mediante el uso de sustituciones apropiadas.

9)$\displaystyle ∫\frac{\ln x}{x}\,dx$

10)$\displaystyle ∫\frac{dx}{x(\ln x)^2}$

Contestar: $\displaystyle ∫\frac{dx}{x(\ln x)^2} \quad = \quad −\frac{1}{\ln x}+C$

11)$\displaystyle ∫\frac{dx}{x\ln x}\quad (x>1)$

12)$\displaystyle ∫\frac{dx}{x\ln x\ln(\ln x)}$

Contestar: $\displaystyle ∫\frac{dx}{x\ln x\ln(\ln x)} \quad = \quad \ln(\ln(\ln x))+C$

13)$\displaystyle ∫\tan θ\,dθ$

14)$\displaystyle ∫\frac{\cos x−x\sin x}{x\cos x}\,dx$

Contestar: $\displaystyle ∫\frac{\cos x−x\sin x}{x\cos x}\,dx \quad = \quad \ln(x\cos x)+C$

15)$\displaystyle ∫\frac{\ln(\sin x)}{\tan x}\,dx$

16)$\displaystyle ∫\ln(\cos x)\tan x\,dx$

Contestar: $\displaystyle ∫\ln(\cos x)\tan x\,dx \quad = \quad −\dfrac{1}{2}(\ln(\cos(x)))^2+C$

17)$\displaystyle ∫xe^{−x^2}\,dx$

18)$\displaystyle ∫x^2e^{−x^3}\,dx$

Contestar: $\displaystyle ∫x^2e^{−x^3}\,dx \quad = \quad \dfrac{−e^{−x^3}}{3}+C$

19)$\displaystyle ∫e^{\sin x}\cos x\,dx$

20)$\displaystyle ∫e^{\tan x}\sec^2 x\,dx$

Contestar: $\displaystyle ∫e^{\tan x}\sec^2 x\,dx\quad = \quad e^{\tan x}+C$

21)$\displaystyle ∫\frac{e^{\ln x}}{x}\,dx $

22)$\displaystyle ∫\frac{e^{\ln(1−t)}}{1−t}\,dt$

Contestar: $\displaystyle ∫\frac{e^{\ln(1−t)}}{1−t}\,dt = \int \frac{1-t}{1-t}\,dt = \int 1\, dt \quad = \quad t+C$

En los ejercicios 23 - 28, verificar por diferenciación eso$\displaystyle ∫\ln x\,dx=x(\ln x−1)+C$, luego utilizar los cambios apropiados de variables para computar la integral.

23)$\displaystyle ∫\ln x\,dx$ (Pista:$\displaystyle ∫\ln x\,dx=\frac{1}{2}∫x\ln(x^2)\,dx$)

24)$\displaystyle ∫x^2\ln^2 x\,dx$

Contestar: $\displaystyle ∫x^2\ln^2 x\,dx \quad = \quad \dfrac{1}{9}x^3(\ln(x^3)−1)+C$

25)$\displaystyle ∫\frac{\ln x}{x^2}\,dx$ (Pista: Set$u=\dfrac{1}{x}.)$

26)$\displaystyle ∫\frac{\ln x}{\sqrt{x}}\,dx$ (Pista: Set$u=\sqrt{x}.)$

Contestar: $ \displaystyle ∫\frac{\ln x}{\sqrt{x}}\,dx \quad = \quad 2\sqrt{x}(\ln x−2)+C$

27) Escribir una integral para expresar el área bajo la gráfica de$y=\dfrac{1}{t}$ desde$ t=1$ hasta$e^x$ y evaluar la integral.

28) Escribir una integral para expresar el área bajo la gráfica de$y=e^t$ entre$t=0$ y$t=\ln x$, y evaluar la integral.

Contestar: $\displaystyle ∫^{\ln x}_0e^t\,dt=e^t\bigg|^{\ln x}_0=e^{\ln x}−e^0=x−1$

En los ejercicios 29 - 35, utilizar sustituciones apropiadas para expresar las integrales trigonométricas en términos de composiciones con logaritmos.

29)$\displaystyle ∫\tan(2x)\,dx$

30)$\displaystyle ∫\frac{\sin(3x)−\cos(3x)}{\sin(3x)+\cos(3x)}\,dx$

Contestar: $ \displaystyle ∫\frac{\sin(3x)−\cos(3x)}{\sin(3x)+\cos(3x)}\,dx \quad = \quad −\frac{1}{3}\ln|\sin(3x)+\cos(3x)| + C$

31)$\displaystyle ∫\frac{x\sin(x^2)}{\cos(x^2)}\,dx$

32)$\displaystyle ∫x\csc(x^2)\,dx$

Contestar: $ \displaystyle ∫x\csc(x^2)\,dx \quad = \quad −\frac{1}{2}\ln∣\csc(x^2)+\cot(x^2)∣+C$

33)$\displaystyle ∫\ln(\cos x)\tan x\,dx$

34)$\displaystyle ∫\ln(\csc x)\cot x\,dx$

Contestar: $ \displaystyle ∫\ln(\csc x)\cot x\,dx \quad = \quad −\frac{1}{2}(\ln(\csc x))^2+C$

35)$\displaystyle ∫\frac{e^x−e^{−x}}{e^x+e^{−x}}\,dx$

En los ejercicios 36 - 40, evaluar la integral definida.

36)$\displaystyle ∫^2_1\frac{1+2x+x^2}{3x+3x^2+x^3}\,dx$

Contestar: $\displaystyle ∫^2_1\frac{1+2x+x^2}{3x+3x^2+x^3}\,dx \quad = \quad \frac{1}{3}\ln\left(\tfrac{26}{7}\right)$

37)$\displaystyle ∫^{π/4}_0\tan x\,dx$

38)$\displaystyle ∫^{π/3}_0\frac{\sin x−\cos x}{\sin x+\cos x}\,dx$

Contestar: $\displaystyle ∫^{π/3}_0\frac{\sin x−\cos x}{\sin x+\cos x}\,dx \quad = \quad \ln(\sqrt{3}−1)$

39)$\displaystyle ∫^{π/2}_{π/6}\csc x\,dx$

40)$\displaystyle ∫^{π/3}_{π/4}\cot x\,dx$

Contestar: $\displaystyle ∫^{π/3}_{π/4}\cot x\,dx \quad = \quad \frac{1}{2}\ln\frac{3}{2}$

En los ejercicios 41 - 46, integrar utilizando la sustitución indicada.

41)$\displaystyle ∫\frac{x}{x−100}\,dx;\quad u=x−100$

42)$\displaystyle ∫\frac{y−1}{y+1}\,dy;\quad u=y+1$

Contestar: $ \displaystyle ∫\frac{y−1}{y+1}\,dy \quad = \quad y−2\ln|y+1|+C$

43)$\displaystyle ∫\frac{1−x^2}{3x−x^3}\,dx;\quad u=3x−x^3$

44)$\displaystyle ∫\frac{\sin x+\cos x}{\sin x−\cos x}\,dx;\quad u=\sin x−\cos x$

Contestar: $\displaystyle ∫\frac{\sin x+\cos x}{\sin x−\cos x}\,dx \quad=\quad \ln|\sin x−\cos x|+C$

45)$\displaystyle ∫e^{2x}\sqrt{1−e^{2x}}\,dx;\quad u=e^{2x}$

46)$\displaystyle ∫\ln(x)\frac{\sqrt{1−(\ln x)^2}}{x}\,dx;\quad u=\ln x$

Contestar: $\displaystyle ∫\ln(x)\frac{\sqrt{1−(\ln x)^2}}{x}\,dx \quad = \quad −\frac{1}{3}(1−(\ln x^2))^{3/2}+C$

47)$\displaystyle \int \frac{\sqrt{x}}{\sqrt{x} + 2}\,dx; \quad u = \sqrt{x} + 2$

Contestar: $\displaystyle \int \frac{\sqrt{x}}{\sqrt{x} + 2}\,dx \quad = \quad \left( \sqrt{x} + 2 \right)^2 - 8\left( \sqrt{x} + 2 \right) + 8\ln\left( \sqrt{x} + 2 \right) + C$

48)$\displaystyle \int e^x\sec(e^x+1)\tan(e^x+1)\,dx; \quad u = e^{x} + 1$

Contestar: $\displaystyle \int e^x\sec(e^x+1)\tan(e^x+1)\,dx \quad = \quad \sec(e^x+1) + C$

En los ejercicios 49 - 54, indique si la aproximación del punto final derecho sobreestima o subestima el área exacta. Después, calcule la estimación del punto final correcto$R_{50}$ y resuelva para el área exacta.

49) [T]$y=e^x$ sobre$[0,1]$

50) [T]$ y=e^{−x}$ sobre$[0,1]$

Contestar: Dado que$f$ es decreciente, la estimación del punto final correcto subestima el área.
Solución exacta:$\dfrac{e−1}{e},\quad R_{50}=0.6258$.

51) [T]$y=\ln(x)$ sobre$[1,2]$

52) [T]$y=\dfrac{x+1}{x^2+2x+6}$ sobre$ [0,1]$

Contestar: Dado que$f$ va en aumento, la estimación del punto final correcto sobreestima el área.
Solución exacta:$\dfrac{2\ln(3)−\ln(6)}{2},\quad R_{50}=0.2033.$

53) [T]$y=2^x$ sobre$[−1,0]$

54) [T]$ y=−2^{−x}$ sobre$ [0,1]$

Contestar: Dado que$f$ está aumentando, la estimación del punto final correcto sobreestima el área (el área real es un número negativo mayor).
Solución exacta:$−\dfrac{1}{\ln(4)},\quad R_{50}=−0.7164.$

En los ejercicios 55 - 58,$f(x)≥0$ para$a≤x≤b$. Encuentra el área debajo de la gráfica de$f(x)$ entre los valores dados$a$ y$b$ integrando.

55)$f(x)=\dfrac{\log_{10}(x)}{x};\quad a=10,b=100$

56)$f(x)=\dfrac{\log_2(x)}{x};\quad a=32,b=64$

Contestar: $\dfrac{11}{2}\ln 2$

57)$f(x)=2^{−x};\quad a=1,b=2$

58)$f(x)=2^{−x};\quad a=3,b=4$

Contestar: $\dfrac{1}{\ln(65,536)}$

59) Encuentra el área debajo de la gráfica de la función$ f(x)=xe^{−x^2}$ entre$x=0$ y$x=5$.

60) Calcular la integral de$f(x)=xe^{−x^2}$ y encontrar el valor más pequeño de$N$ tal manera que el área bajo la gráfica$f(x)=xe^{−x^2}$ entre$ x=N$ y$x=N+10$ es, a lo sumo,$0.01$.

Contestar: $\displaystyle ∫^{N+1}_Nxe^{−x^2}\,dx=\frac{1}{2}(e^{−N^2}−e^{−(N+1)^2}).$La cantidad es menor que$0.01$ cuando$N=2$.

61) Encuentra el límite, como$N$ tiende al infinito, del área bajo la gráfica de$f(x)=xe^{−x^2}$ entre$x=0$ y$x=5$.

62) Demostrar que$\displaystyle ∫^b_a\frac{dt}{t}=∫^{1/a}_{1/b}\frac{dt}{t}$ cuando$0<a≤b$.

Contestar: $\displaystyle ∫^b_a\frac{dx}{x}=\ln(b)−\ln(a)=\ln(\frac{1}{a})−\ln(\frac{1}{b})=∫^{1/a}_{1/b}\frac{dx}{x}$

63) Supongamos que$f(x)>0$ para todos$x$ y eso$f$ y$g$ son diferenciables. Utilice la identidad$ f^g=e^{g\ln f}$ y la regla de la cadena para encontrar la derivada de$ f^g$.

64) Utilizar el ejercicio anterior para encontrar la antiderivada de$h(x)=x^x(1+\ln x)$ y evaluar$\displaystyle ∫^3_2x^x(1+\ln x)\,dx$.

Contestar: 23

65) Demostrar que si$c>0$, entonces la integral$\frac{1}{x}$ de de$ac$ a$bc$ $(\text{for}\,0<a<b)$es la misma que la integral de$\frac{1}{x}$ de$a$ a $b$.

Los siguientes ejercicios están destinados a derivar las propiedades fundamentales del tronco natural a partir de la definición$\displaystyle \ln(x)=∫^x_1\frac{dt}{t}$, utilizando propiedades de la integral definida y sin hacer más suposiciones.

66) Utilizar la identidad$\displaystyle \ln(x)=∫^x_1\frac{dt}{t}$ para derivar la identidad$\ln\left(\dfrac{1}{x}\right)=−\ln x$.

Contestar: Podemos suponer que$x>1$, entonces$\dfrac{1}{x}<1.$ entonces,$\displaystyle ∫^{1/x}_{1}\frac{dt}{t}$. Ahora haga la sustitución$u=\dfrac{1}{t}$, así$du=−\dfrac{dt}{t^2}$ y$\dfrac{du}{u}=−\dfrac{dt}{t}$, y cambie los puntos finales:$\displaystyle ∫^{1/x}_1\frac{dt}{t}=−∫^x_1\frac{du}{u}=−\ln x.$

67) Utilizar un cambio de variable en la integral$\displaystyle ∫^{xy}_1\frac{1}{t}\,dt$ para mostrar que$\ln xy=\ln x+\ln y$ para$ x,y>0$.

68) Utilizar la identidad$\displaystyle \ln x=∫^x_1\frac{dt}{x}$ para mostrar que$\ln(x)$ es una función creciente de$x$ on$[0,∞)$, y utilizar los ejercicios anteriores para demostrar que el rango de$\ln(x)$ es$(−∞,∞)$. Sin más suposiciones, concluya que$\ln(x)$ tiene una función inversa definida en$ (−∞,∞).$

69) Fingir, por el momento, que no sabemos que$e^x$ es la función inversa de$\ln(x)$, pero hay que tener en cuenta que$\ln(x)$ tiene una función inversa definida en$ (−∞,∞)$. Llámenlo$E$. Usa la identidad$\ln xy=\ln x+\ln y$ para deducir eso$E(a+b)=E(a)E(b)$ para cualquier número real$a$,$b$.

70) Fingir, por el momento, que no sabemos que$ e^x$ es la función inversa de$\ln x$, pero hay que tener en cuenta que$ \ln x$ tiene una función inversa definida en$(−∞,∞)$. Llámenlo$E$. Demostrar que$E'(t)=E(t).$

Contestar: $x=E(\ln(x)).$Entonces,$1=\dfrac{E'(\ln x)}{x}$ o$x=E'(\ln x)$. Dado que cualquier número se$t$ puede escribir$t=\ln x$ para algunos$x$, y para tal$t$ tenemos$x=E(t)$, se deduce que para cualquier$t,\,E'(t)=E(t).$

71) El seno integral, definido como$\displaystyle S(x)=∫^x_0\frac{\sin t}{t}\,dt$ es una cantidad importante en ingeniería. Aunque no tiene una fórmula simple cerrada, es posible estimar su comportamiento para grandes$x$. Muéstralo para$k≥1,\quad |S(2πk)−S(2π(k+1))|≤\dfrac{1}{k(2k+1)π}.$ (Pista:$ \sin(t+π)=−\sin t$)

72) [T] La distribución normal en probabilidad viene dada por$p(x)=\dfrac{1}{σ\sqrt{2π}}e^{−(x−μ)^2/2σ^2}$, donde$σ$ está la desviación estándar y$μ$ es la media. La distribución normal estándar en probabilidad,$p_s$, corresponde a$ μ=0$ y$σ=1$. Calcular las estimaciones de punto final izquierdo$R_{10}$ y$R_{100}$ de$\displaystyle ∫^1_{−1}\frac{1}{\sqrt{2π}}e^{−x^{2/2}}\,dx.$

Contestar: $R_{10}=0.6811,\quad R_{100}=0.6827$

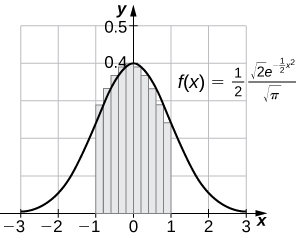
$Una gráfica de la función f (x) = .5 * (sqrt (2) *e^ (-.5x^2))/sqrt (pi). Es una curva de apertura hacia abajo que es simétrica a través del eje y, cruzando aproximadamente (0, .4). Se acerca a 0 a medida que x va al infinito positivo y negativo. Entre 1 y -1, se dibujan diez rectángulos para una estimación del punto final derecho del área bajo la curva.$

73) [T] Calcular las estimaciones de punto final correcto$R_{50}$ y$R_{100}$ de$\displaystyle ∫^5_{−3}\frac{1}{2\sqrt{2π}}e^{−(x−1)^2/8}$.

Colaboradores y Atribuciones

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) added problems 47-48 to Section 5.6 exercises.