6.1E: Ejercicios para la Sección 6.1

Última actualización
Guardar como PDF

Page ID: 116194

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Para los ejercicios 1 - 2, determinar el área de la región entre las dos curvas en la figura dada integrando sobre el$x$ eje.

1)$y=x^2−3$ y$y=1$

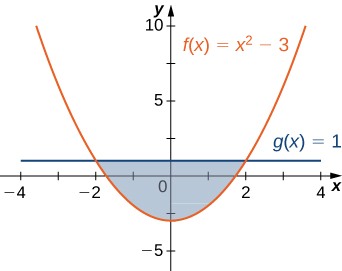
$Esta figura tiene dos gráficas. Son las funciones f (x) = x^2-3y g (x) =1. Entre estas gráficas se encuentra una región sombreada, delimitada arriba por g (x) y abajo por f (x). El área sombreada está entre x=-2 y x=2.$

Contestar: $\dfrac{32}{3} \, \text{units}^2$

2)$y=x^2$ y$y=3x+4$

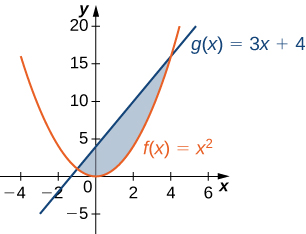
$Esta figura tiene dos gráficas. Son las funciones f (x) = x^2 y g (x) = 3x+4. Entre estas gráficas se encuentra una región sombreada, delimitada arriba por g (x) y abajo por g (x).$

Para los ejercicios 3 - 4, divida la región entre las dos curvas en dos regiones más pequeñas, luego determine el área integrando sobre el$x$ eje. Ten en cuenta que tendrás dos integrales para resolver.

3)$y=x^3$ y$ y=x^2+x$

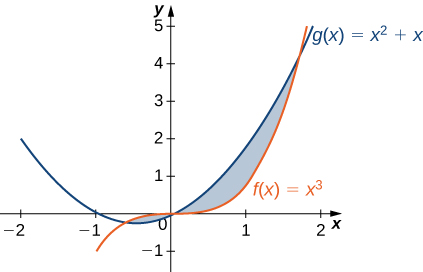
$Esta figura tiene dos gráficas. Son las funciones f (x) = x^3 y g (x) = x^2+x Estas gráficas se cruzan dos veces. Las regiones entre las intersecciones están sombreadas. La primera región está delimitada arriba por f (x) y por debajo por g (x). La segunda región está delimitada arriba por g (x) y por debajo por f (x).$

Contestar: $\dfrac{13}{12}\, \text{units}^2$

4)$y=\cos θ$ y$ y=0.5$, para$ 0≤θ≤π$

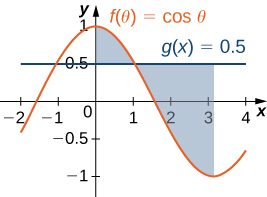
$Esta figura tiene dos gráficas. Son las funciones f (theta) = cos (theta) y g (x) = 0.5. Estas gráficas se cruzan dos veces. Las regiones entre las intersecciones están sombreadas. La primera región está delimitada arriba por f (x) y por debajo por g (x). La segunda región está delimitada arriba por g (x) y por debajo por f (x).$

Para los ejercicios 5-6, determinar el área de la región entre las dos curvas integrándose sobre el$y$ eje -eje.

5)$x=y^2$ y$x=9$

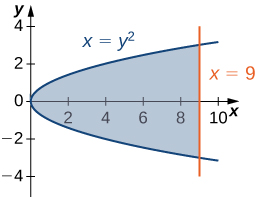
$Esta figura tiene dos gráficas. Son las ecuaciones x=y^2 y x=9. La región entre las gráficas está sombreada. Es horizontal, entre el eje y y la línea x=9.$

Contestar: $36 \, \text{units}^2$

6)$y=x$ y$ x=y^2$

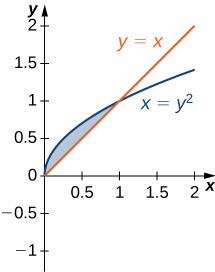
$Esta figura tiene dos gráficas. Son las ecuaciones y=x y x=y^2. La región entre las gráficas está sombreada, delimitada arriba por x=y^2 y abajo por y=x.$

Para los ejercicios 7 - 13, grafica las ecuaciones y sombrea el área de la región entre las curvas. Determinar su área integrándose sobre el$x$ eje.

7)$y=x^2$ y$y=−x^2+18x$

Contestar

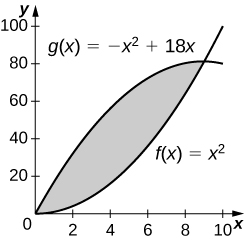
$Esta figura tiene dos gráficas. Son las funciones f (x) =x^2 y g (x) =-x^2+18x. La región entre las gráficas está sombreada, delimitada arriba por g (x) y abajo por f (x). Está en el primer cuadrante.$

243 unidades cuadradas

8)$y=\dfrac{1}{x}, \quad y=\dfrac{1}{x^2}$, y$x=3$

9)$y=\cos x$ y$y=\cos^2x$ en$x \in [−π,π]$

Contestar

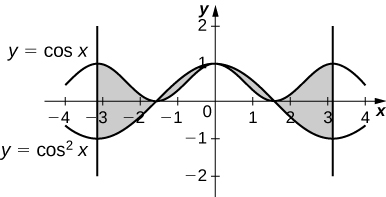
$Esta figura tiene dos gráficas. Son las funciones y=cos (x) e y=cos^2 (x). Las gráficas son periódicas y se asemejan a ondas. Hay cuatro regiones creadas por las intersecciones de las curvas. Las áreas están sombreadas.$

4 unidades cuadradas

10)$y=e^x,\quad y=e^{2x−1}$, y$x=0$

11)$y=e^x, \quad y=e^{−x}, \quad x=−1$ y$x=1$

Contestar

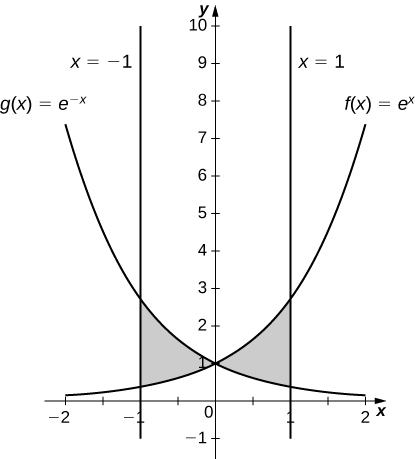
$Esta figura tiene dos gráficas. Son las funciones f (x) =e^x y g (x) =e^-x. Hay dos regiones sombreadas. En el segundo cuadrante la región está delimitada por x=-1, g (x) arriba y f (x) abajo. La segunda región está en el primer cuadrante y está delimitada por f (x) arriba, g (x) por debajo y x=1.$

$\dfrac{2(e−1)^2}{e}\, \text{units}^2$

12)$ y=e, \quad y=e^x,$ y$y=e^{−x}$

13)$y=|x|$ y$y=x^2$

Contestar

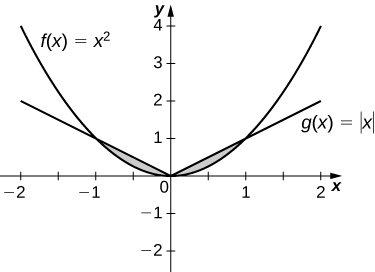
$Esta figura tiene dos gráficas. Son las funciones f (x) =x^2 y g (x) =valor absoluto de x. Hay dos regiones sombreadas. La primera región está en el segundo cuadrante y está entre g (x) arriba y f (x) abajo. La segunda región se encuentra en el primer cuadrante y está delimitada arriba por g (x) y por debajo por f (x).$

$\dfrac{1}{3}\, \text{units}^2$

Para los ejercicios 14 - 19, grafica las ecuaciones y sombrea el área de la región entre las curvas. Si es necesario, divida la región en subregiones para determinar toda su área.

14)$y=\sin(πx),\quad y=2x,$ y$x>0$

15)$y=12−x,\quad y=\sqrt{x},$ y$y=1$

Contestar

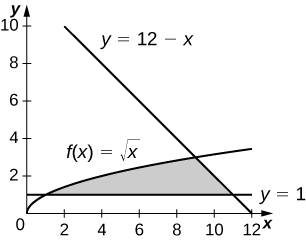
$Esta cifra tiene tres gráficas. Son las funciones f (x) =squareroot de x, y=12-x, e y=1. La región entre las gráficas está sombreada, delimitada arriba y a la izquierda por f (x), arriba y a la derecha por la línea y=12-x, y abajo por la línea y=1. Está en el primer cuadrante.$

$\dfrac{34}{3}\, \text{units}^2$

16)$y=\sin x$ y$y=\cos x$ más$x \in [−π,π]$

17)$y=x^3$ y$y=x^2−2x$ más$x \in [−1,1]$

Contestar

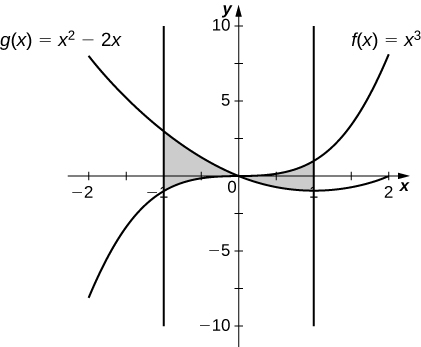
$Esta figura tiene dos gráficas. Son las funciones f (x) =x^3 y g (x) =x^2-2x. Hay dos regiones sombreadas entre las gráficas. La primera región está delimitada a la izquierda por la línea x=-2, arriba por g (x) y abajo por f (x). La segunda región está delimitada arriba por f (x), abajo por g (x) y a la derecha por la línea x=2.$

$\dfrac{5}{2}\, \text{units}^2$

18)$y=x^2+9$ y$ y=10+2x$ más$x \in [−1,3]$

19)$y=x^3+3x$ y$y=4x$

Contestar

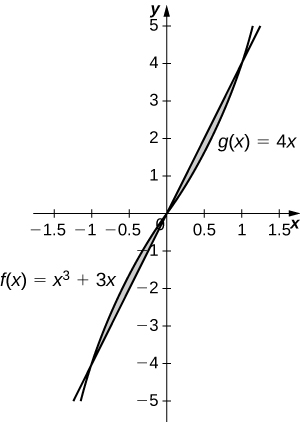
$Esta figura tiene dos gráficas. Son las funciones f (x) =x^3+3x y g (x) =4x. Hay dos regiones sombreadas entre las gráficas. La primera región está delimitada arriba por f (x) y por debajo por g (x). La segunda región está delimitada arriba por g (x), abajo por f (x).$

$\dfrac{1}{2}\, \text{units}^2$

Para los ejercicios 20 -25, grafica las ecuaciones y sombrea el área de la región entre las curvas. Determinar su área integrándose sobre el$y$ eje.

20)$x=y^3$ y$ x = 3y−2$

21)$x=y$ y$ x=y^3−y$

Contestar

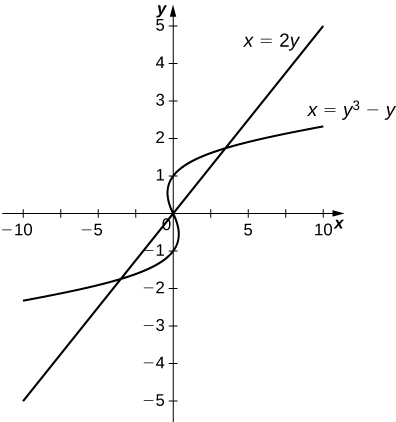
$Esta figura tiene dos gráficas. Son las ecuaciones x=2y y x=y^3-y. Las gráficas se cruzan en el tercer cuadrante y nuevamente en el primer cuadrante formando dos regiones cerradas entre ellas.$

$\dfrac{9}{2}\, \text{units}^2$

22)$x=−3+y^2$ y$ x=y−y^2$

23)$y^2=x$ y$x=y+2$

Contestar

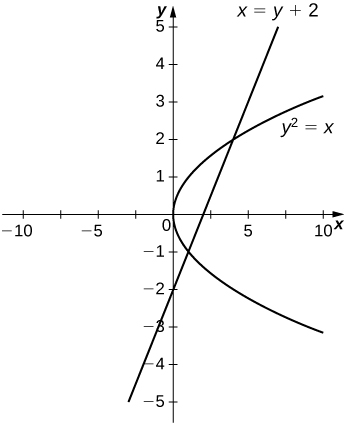
$Esta figura tiene dos gráficas. Son las ecuaciones x=y+2 e y^2=x Las gráficas se cruzan formando una región entre ellas$

$\dfrac{9}{2}\, \text{units}^2$

24)$x=|y|$ y$2x=−y^2+2$

25)$x=\sin y,\quad x=\cos(2y),\quad y=π/2$, y$ y=−π/2$

Contestar

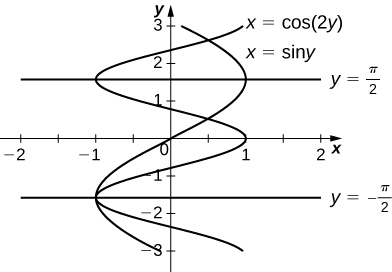
$Esta figura tiene dos gráficas. Son las ecuaciones x=cos (y) y x=sin (y). Las gráficas se cruzan formando dos regiones delimitadas arriba por la línea y=pi/2 y abajo por la línea y=-pi/2.$

$\dfrac{3\sqrt{3}}{2}\, \text{units}^2$

Para los ejercicios 26 - 37, grafica las ecuaciones y sombrea el área de la región entre las curvas. Determine su área integrando sobre el$x$ eje o$y$ eje, lo que le parezca más conveniente.

26)$x=y^4$ y$x=y^5$

27)$y=xe^x,\quad y=e^x,\quad x=0$, y$x=1$.

Contestar

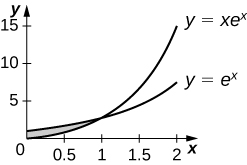
$Esta figura tiene dos gráficas. Son las ecuaciones y=xe^x e y=e^x Las gráficas se cruzan formando una región entre ellas en el primer cuadrante.$

$e^{−2}\, \text{units}^2$

28)$y=x^6$ y$y=x^4$

29)$x=y^3+2y^2+1$ y$x=−y^2+1$

Responder

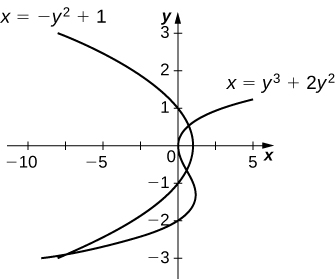
$Esta figura tiene dos gráficas. Son las ecuaciones x=-y^2+1 y x=y^3+2y^2. Las gráficas se cruzan formando dos regiones entre ellas.$

$\dfrac{27}{4}\, \text{units}^2$

30)$ y=|x|$ y$ y=x^2−1$

31)$y=4−3x$ y$y=\dfrac{1}{x}$

Responder

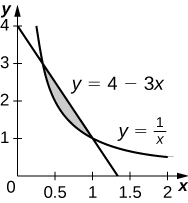
$Esta figura tiene dos gráficas. Son las ecuaciones y=4-3x e y=1/x Las gráficas se cruzan, teniendo región entre ellas sombreada. La región se encuentra en el primer cuadrante.$

$\left(\dfrac{4}{3}−\ln(3)\right)\, \text{units}^2$

32)$y=\sin x,\quad x=−π/6,\quad x=π/6,$ y$y=\cos^3 x$

33)$y=x^2−3x+2$ y$ y=x^3−2x^2−x+2$

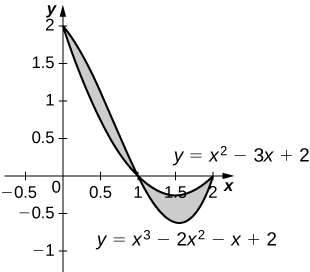
Responder: $Esta figura tiene dos gráficas. Son las ecuaciones y=x^2-3x+2 e y=x^3-2x^2-x+2. Las gráficas se cruzan, teniendo región entre ellas sombreada.$
$\dfrac{1}{2}$unidades cuadradas

34)$y=2\cos^3(3x),\quad y=−1,\quad x=\dfrac{π}{4},$ and $ x=−\dfrac{π}{4}$

35)$y+y^3=x$ and $2y=x$

Responder

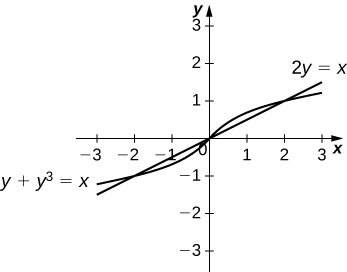
$Esta figura tiene dos gráficas. Son las ecuaciones 2y=x e y+y^3=x Las gráficas se cruzan formando dos regiones. Las regiones están sombreadas.$

$\dfrac{1}{2}$unidades cuadradas

36)$ y=\sqrt{1−x^2}$ y$y=x^2−1$

37)$y=\cos^{−1}x,\quad y=\sin^{−1}x,\quad x=−1,$ y$ x=1$

Responder

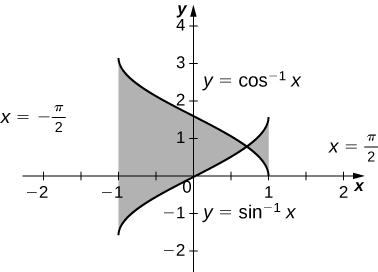
$Esta figura tiene dos gráficas. Son las ecuaciones y=arccos (x) e y=arcsin (x). Las gráficas se cruzan formando dos regiones. La primera región está delimitada a la izquierda por x=-1. La segunda región está delimitada a la derecha por x=1. Ambas regiones están sombreadas.$

$−2(\sqrt{2}−π)$unidades cuadradas

Para los ejercicios 38 - 47, encuentra el área exacta de la región delimitada por las ecuaciones dadas si es posible. Si no puede determinar analíticamente los puntos de intersección, utilice una calculadora para aproximar los puntos de intersección con tres decimales y determinar el área aproximada de la región.

38) [T]$x=e^y$ y$y=x−2$

39) [T]$y=x^2$ y$y=\sqrt{1−x^2}$

Responder: $1.067$unidades cuadradas

40) [T]$y=3x^2+8x+9$ y$3y=x+24$

41) [T]$x=\sqrt{4−y^2}$ y$ y^2=1+x^2$

Responder: $0.852$unidades cuadradas

42) [T]$x^2=y^3$ y$x=3y$

43) [T]$y=\sin^3x+2,\quad y=\tan x,\quad x=−1.5,$ y$x=1.5$

Responder: $7.523$unidades cuadradas

44) [T]$y=\sqrt{1−x^2}$ y$y^2=x^2$

45) [T]$y=\sqrt{1−x^2}$ y$y=x^2+2x+1$

Responder: $\dfrac{3π−4}{12}$unidades cuadradas

46) [T]$x=4−y^2$ y$ x=1+3y+y^2$

47) [T]$y=\cos x,\quad y=e^x,\quad x=−π,\quad$ y$\quad x=0$

Responder: $1.429$unidades cuadradas

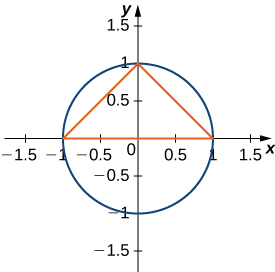
48) El triángulo más grande con una base en el$x$ eje -que encaja dentro de la mitad superior del círculo unitario$y^2+x^2=1$ viene dado por$ y=1+x$ y$ y=1−x$. Consulte la siguiente figura. ¿Cuál es el área dentro del semicírculo pero fuera del triángulo?

$Esta figura tiene la gráfica de un círculo con centro en el origen y radio de 1. Hay un triángulo inscrito con base en el eje x de -1 a 1 y la tercera esquina en el punto y=1.$

49) Una fábrica que vende celulares tiene una función de costo marginal$C(x)=0.01x^2−3x+229$, donde$x$ representa el número de celulares, y una función de ingresos marginales dada por$R(x)=429−2x.$ Encuentra el área entre las gráficas de estas curvas y$x=0.$ ¿Qué representa esta área?

Responder: $33,333.33 beneficio total para 200 celulares vendidos

50) Un parque de diversiones tiene una función de costo marginal$C(x)=1000e−x+5$, donde$x$ representa el número de boletos vendidos, y una función marginal de ingresos dada por$R(x)=60−0.1x$. Encuentra el beneficio total generado al vender$550$ boletos. Utilice una calculadora para determinar los puntos de intersección, si es necesario, a dos decimales.

51) La tortuga versus la liebre: La velocidad de la liebre viene dada por la función sinusoidal$H(t)=1−\cos((πt)/2)$ mientras que la velocidad de la tortuga es$T(t)=(1/2)\tan^{−1}(t/4)$, donde$t$ se mide el tiempo en horas y la velocidad se mide en millas por hora. Encuentra el área entre las curvas de tiempo$t=0$ a la primera vez después de una hora cuando la tortuga y la liebre viajan a la misma velocidad. ¿Qué representa? Use una calculadora para determinar los puntos de intersección, si es necesario, con una precisión de tres decimales.

Responder: $3.263$mi representa lo lejos que está la liebre de la tortuga

52) La tortuga versus la liebre: La velocidad de la liebre viene dada por la función sinusoidal$H(t)=(1/2)−(1/2)\cos(2πt)$ mientras que la velocidad de la tortuga es$T(t)=\sqrt{t}$, donde$t$ se mide el tiempo en horas y la velocidad se mide en kilómetros por hora. Si la carrera termina en 1 hora, ¿quién ganó la carrera y por cuánto? Use una calculadora para determinar los puntos de intersección, si es necesario, con una precisión de tres decimales.

Para los ejercicios 53 - 55, encuentra el área entre las curvas integrando con respecto$x$ y luego con respecto a$y$. ¿Un método es más fácil que el otro? ¿Obtienes la misma respuesta?

53)$y=x^2+2x+1$ y$y=−x^2−3x+4$

Responder: $\dfrac{343}{24}$unidades cuadradas

54)$y=x^4$ y$x=y^5$

55)$x=y^2−2$ y$x=2y$

Responder: $4\sqrt{3}$unidades cuadradas

Para los ejercicios 56 - 57, resuelve usando cálculo, luego revisa tu respuesta con geometría.

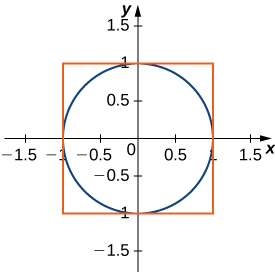
56) Determinar las ecuaciones para los lados del cuadrado que toca el círculo unitario en los cuatro lados, como se ve en la siguiente figura. Encuentra el área entre el perímetro de esta plaza y el círculo unitario. ¿Hay otra manera de resolver esto sin usar cálculo?

$Esta figura es la gráfica de un círculo centrado en el origen con radio de 1. Hay un cuadrado circunscrito alrededor del círculo.$

57) Encuentra el área entre el perímetro del círculo unitario y el triángulo creado a partir de$y=2x+1,\,y=1−2x$ y$y=−\dfrac{3}{5}$, como se ve en la siguiente figura. ¿Hay alguna manera de resolver esto sin usar cálculo?

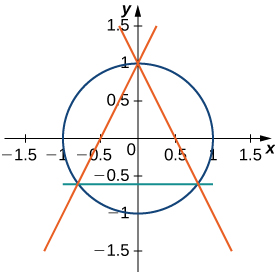
$Esta figura es la gráfica de un círculo centrado en el origen con radio de 1. Hay tres líneas que cruzan el círculo. Las líneas se cruzan con el círculo en tres puntos para formar un triángulo dentro del círculo.$

Responder: $ \left(π−\dfrac{32}{25}\right)$unidades cuadradas

Colaboradores

Template:ContribOpenStaxCalc