6.3E: Ejercicios para la Sección 6.3

Última actualización
Guardar como PDF

Page ID: 116168

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Para los ejercicios 1 - 6, encuentra el volumen generado cuando la región entre las dos curvas se gira alrededor del eje dado. Utilice tanto el método de la carcasa como el método de la arandela. Utilice la tecnología para graficar las funciones y dibujar una rebanada típica a mano.

1) [T] Sobre la curva de$ y=3x,$$x=0,$ y$ y=3$ girado alrededor del$y$ eje.

2) [T] Bajo la curva de$ y=3x,$$x=0$, y$ x=3$ girado alrededor del$y$ eje.

Responder

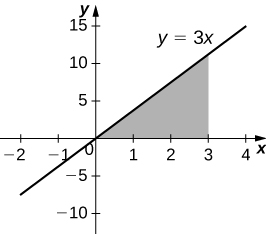
$Esta figura es una gráfica en el primer cuadrante. Es la línea y=3x. Debajo de la línea y por encima del eje x hay una región sombreada. La región está delimitada a la derecha en x=3.$

$V = 54π$unidades ³

3) [T] Sobre la curva de$ y=3x,$$x=0$, y$ y=3$ girado alrededor del$x$ eje.

4) [T] Bajo la curva de$ y=3x,$$x=0,$ y$ x=3$ girado alrededor del$x$ eje.

Responder

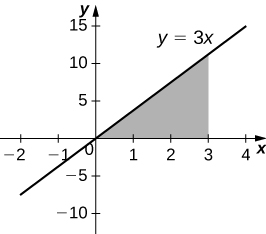
$Esta figura es una gráfica en el primer cuadrante. Es la línea y=3x. Debajo de la línea y por encima del eje x hay una región sombreada. La región está delimitada a la derecha en x=3.$

$V = 81π$unidades ³

5) [T] Bajo la curva de$ y=2x^3,\;x=0,$ y$ x=2$ girado alrededor del$y$ eje.

6) [T] Bajo la curva de$ y=2x^3,\;x=0,$ y$ x=2$ girado alrededor del$x$ eje.

Responder

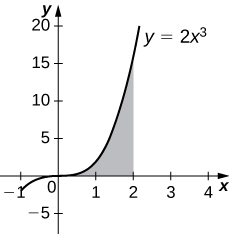
$Esta figura es una gráfica en el primer cuadrante. Es la curva creciente y=2x^3. Bajo la curva y por encima del eje x hay una región sombreada. La región está delimitada a la derecha en x=2.$

$V = \frac{512π}{7}$unidades ³

Para los ejercicios 7 - 16, use conchas para encontrar los volúmenes de los sólidos dados. Tenga en cuenta que las regiones giradas se encuentran entre la curva y el$x$ eje y se rotan alrededor del$y$ eje.

7)$ y=1−x^2,$$x=0,$ y$ x=1$

8)$ y=5x^3,$$x=0$, y$ x=1$

Responder: $V = 2π$unidades ³

9)$ y=\dfrac{1}{x},$$x=1,$ y$ x=100$

10)$ y=\sqrt{1−x^2},$$x=0$, y$ x=1$

Responder: $V= \frac{2π}{3}$unidades ³

11)$ y=\dfrac{1}{1+x^2},$$x=0$, y$ x=3$

12)$ y=\sin x^2,x=0$, y$ x=\sqrt{π}$

Responder: $V= 2π$unidades ³

13)$ y=\dfrac{1}{\sqrt{1−x^2}},$$x=0$, y$ x=\frac{1}{2}$

14)$ y=\sqrt{x},$$x=0$, y$ x=1$

Responder: $V = \frac{4π}{5}$unidades ³

15)$ y=(1+x^2)^3,$$x=0$, y$ x=1$

16)$ y=5x^3−2x^4,$$x=0$, y$ x=2$

Responder: $V= \frac{64π}{3}$unidades ³

Para los ejercicios 17 - 26, use shells para encontrar el volumen generado al rotar las regiones entre la curva dada y$ y=0$ alrededor del$x$ eje.

17)$ y=\sqrt{1−x^2},$$x=0$, y$ x=1$

18)$ y=x^2,$$x=0$, y$ x=2$

Responder: $V = \frac{32π}{5}$unidades ³

19)$ y=e^x,$$x=0$, y$ x=1$

20)$ y=\ln(x),$$x=1$, y$ x=e$

Responder: $V= π(e−2)$unidades ³

21)$ x=\dfrac{1}{1+y^2},$$y=1$, y$ y=4$

22)$ x=\dfrac{1+y^2}{y},$$y=0$, y$ y=2$

Responder: $V= \frac{28π}{3}$unidades ³

23)$ x=\cos y,$$y=0$, y$ y=π$

24)$ x=y^3−4y^2,$$x=−1$, y$ x=2$

Responder: $V= \frac{84π}{5}$unidades ³

25)$ x=ye^y,$$x=−1$, y$ x=2$

26)$ x=e^y\cos y,$$x=0$, y$ x=π$

Responder: $V = e^ππ^2$unidades ³

Para los ejercicios 27 - 36, encuentra el volumen generado cuando la región entre las curvas se gira alrededor del eje dado.

27)$ y=3−x$,$y=0$,$x=0$, y$ x=2$ girado alrededor del$y$ eje.

28)$ y=x^3$,$y=0$,$x=0$, y$ y=8$ girado alrededor del$y$ eje.

Responder: $ V=\frac{64π}{5}$unidades ³

29)$ y=x^2,$$y=x,$ girado alrededor del$y$ eje.

30)$ y=\sqrt{x},$$x=0$, y$ x=1$ girado alrededor de la línea$ x=2.$

Responder: $V=\frac{28π}{15}$unidades ³

31)$ y=\dfrac{1}{4−x},$$x=1,$ y$ x=2$ girado alrededor de la línea$ x=4$.

32)$ y=\sqrt{x}$ y$ y=x^2$ girado alrededor del$y$ eje.

Responder: $V=\frac{3π}{10}$unidades ³

33)$ y=\sqrt{x}$ y$ y=x^2$ girado alrededor de la línea$ x=2$.

34)$ x=y^3,$$y=\dfrac{1}{x},$$x=1$, y$ y=2$ girado alrededor del$x$ eje.

Responder: $ \frac{52π}{5}$unidades ³

35)$ x=y^2$ y$ y=x$ girado alrededor de la línea$ y=2$.

36) [T] Izquierda de$ x=\sin(πy)$, derecha de$ y=x$, alrededor del$y$ eje.

Responder: $V \approx 0.9876$unidades ³

Para los ejercicios 37 - 44, utilice la tecnología para graficar la región. Determine qué método cree que sería más fácil de usar para calcular el volumen generado cuando la función se gira alrededor del eje especificado. Luego, usa tu método elegido para encontrar el volumen.

37) [T]$ y=x^2$ y$ y=4x$ girado alrededor del$y$ eje.

38) [T]$ y=\cos(πx),y=\sin(πx),x=\frac{1}{4}$, y$ x=\frac{5}{4}$ girado alrededor del$y$ eje.

Responder

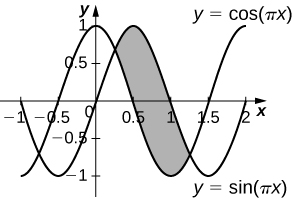
$Esta figura es una gráfica. En la gráfica hay dos curvas, y=cos (pi veces x) e y=sin (pi veces x). Son curvas periódicas que se asemejan a las ondas. Las curvas se cruzan en el primer cuadrante y también en el cuarto cuadrante. La región entre los dos puntos de intersección está sombreada.$

$V = 3\sqrt{2}$unidades ³

39) [T]$ y=x^2−2x,\; x=2,$ y$ x=4$ girado alrededor del$y$ eje.

40) [T]$ y=x^2−2x,\; x=2,$ y$ x=4$ girado alrededor del$x$ eje.

Responder

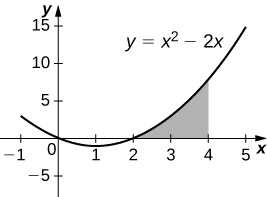
$Esta figura es una gráfica en el primer cuadrante. Es la parábola y=x^2-2x. Bajo la curva y por encima del eje x hay una región sombreada. La región comienza en x=2 y está delimitada a la derecha en x=4.$

$V= \frac{496π}{15}$unidades ³

41) [T]$ y=3x^3−2,\; y=x$, y$ x=2$ girado alrededor del$x$ eje.

42) [T]$ y=3x^3−2,\; y=x$, y$ x=2$ girado alrededor del$y$ eje.

Responder

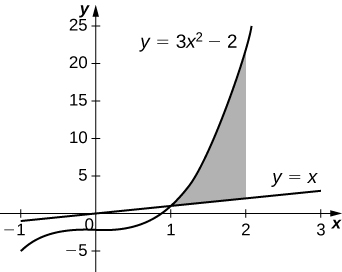
$Esta figura es una gráfica en el primer cuadrante. Hay dos curvas en la gráfica. La primera curva es y=3x^2-2 y la segunda curva es y=x, entre las curvas hay una región sombreada. La región comienza en x=1 y está delimitada a la derecha en x=2.$

$ V = \frac{398π}{15}$unidades ³

43) [T]$ x=\sin(πy^2)$ y$ x=\sqrt{2}y$ girado alrededor del$x$ eje.

44) [T]$ x=y^2,\; x=y^2−2y+1$, y$ x=2$ girado alrededor del$y$ eje.

Responder

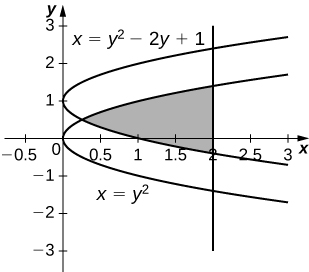
$Esta figura es una gráfica. Hay dos curvas en la gráfica. La primera curva es x=y^2-2y+1 y es una parábola que se abre a la derecha. La segunda curva es x=y^2 y es una parábola que se abre a la derecha. Entre las curvas hay una región sombreada. La región sombreada está delimitada a la derecha en x=2.$

$ V =15.9074$unidades ³

Para los ejercicios 45 - 51, utilice el método de conchas para aproximar los volúmenes de algunos objetos comunes, que se representan en las figuras adjuntas.

45) Usa el método de los proyectiles para encontrar el volumen de una esfera de radio$ r$.

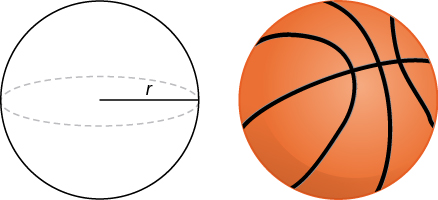
$Esta figura tiene dos imágenes. El primero es un círculo con radio r. El segundo es una básquetbol.$

46) Usa el método de conchas para encontrar el volumen de un cono con radio$ r$ y altura$ h$.

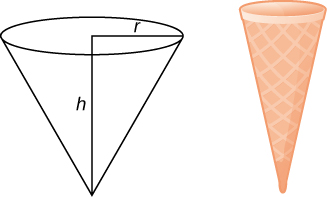
$Esta figura tiene dos imágenes. El primero es un cono boca abajo con radio r y altura h. El segundo es un cono de helado.$

Responder: $V = \frac{1}{3}πr^2h$unidades ³

47) Usa el método de los proyectiles para encontrar el volumen de una elipse$ (x^2/a^2)+(y^2/b^2)=1$ girada alrededor del$x$ eje.

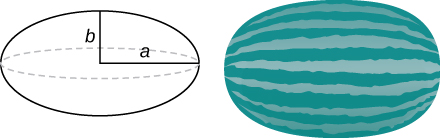
$Esta figura tiene dos imágenes. La primera es una elipse con a la distancia horizontal desde el centro hasta el borde y b la distancia vertical desde el centro hasta el borde superior. El segundo es una sandía.$

48) Utilizar el método de conchas para encontrar el volumen de un cilindro con radio$ r$ y altura$ h$.

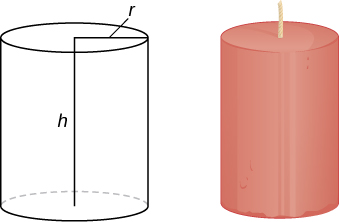
$Esta figura tiene dos imágenes. El primero es un cilindro con radio r y altura h. El segundo es una vela cilíndrica.$

Responder: $V= πr^2h$unidades ³

49) Usa el método de conchas para encontrar el volumen de la rosquilla creada cuando el círculo$ x^2+y^2=4$ se gira alrededor de la línea$ x=4$.

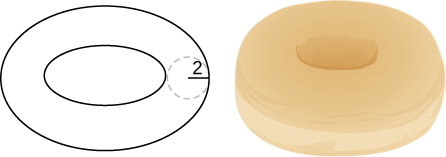
$Esta figura tiene dos imágenes. El primero tiene dos elipses, una dentro de la otra. El radio de la trayectoria entre ellos es de 2 unidades. El segundo es un donuts.$

50) Considerar la región encerrada por las gráficas de$ y=f(x),\; y=1+f(x),\; x=0,\; y=0,$ y$ x=a>0$. ¿Cuál es el volumen del sólido generado cuando esta región se gira alrededor del$y$ eje -eje? Supongamos que la función se define a lo largo del intervalo$ [0,a]$.

Responder: $ V=πa^2$unidades ³

51) Considerar la función$ y=f(x)$, que disminuye de$ f(0)=b$ a$ f(1)=0$. Configura las integrales para determinar el volumen, utilizando tanto el método shell como el método de disco, del sólido generado cuando esta región, con$ x=0$ y$ y=0$, se gira alrededor del$y$ eje -eje. Demostrar que ambos métodos se aproximan al mismo volumen. ¿Qué método es más fácil de aplicar? (Pista: Dado que$ f(x)$ es uno a uno, existe una inversa$ f^{−1}(y)$.)

Colaboradores

Template:ContribOpenStaxCalc