Inicio
Matemáticas
Libro: Cálculo (OpenStax)
6: Aplicaciones de Integración
6.4: Longitud de Arco de una Curva y Área de Superficie

6.4: Longitud de Arco de una Curva y Área de Superficie

Última actualización
Guardar como PDF

Page ID: 116180

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Determinar la longitud de una curva,\(y=f(x)\), entre dos puntos.
Determinar la longitud de una curva,\(x=g(y)\), entre dos puntos.
Encuentra la superficie de un sólido de revolución.

En esta sección, utilizamos integrales definidas para encontrar la longitud del arco de una curva. Podemos pensar en la longitud del arco como la distancia que recorrías si estuvieras caminando por el camino de la curva. Muchas aplicaciones del mundo real implican la longitud del arco. Si se lanza un cohete a lo largo de una trayectoria parabólica, tal vez queramos saber hasta dónde viaja el cohete. O bien, si una curva en un mapa representa una carretera, podríamos querer saber hasta dónde tenemos que conducir para llegar a nuestro destino.

Comenzamos calculando la longitud del arco de las curvas definidas como funciones de\( x\), luego examinamos el mismo proceso para las curvas definidas como funciones de\( y\). (El proceso es idéntico, con los papeles de\( x\) y\( y\) invertido.) Las técnicas que utilizamos para encontrar la longitud del arco se pueden extender para encontrar la superficie de una superficie de revolución, y cerramos la sección con un examen de este concepto.

Longitud de Arco de la Curva y = f (x)

En aplicaciones anteriores de integración, requeríamos que\( f(x)\) la función fuera integrable, o como mucho continua. Sin embargo, para calcular la longitud del arco tenemos un requisito más estricto para\( f(x)\). Aquí, requerimos\( f(x)\) ser diferenciables, y además requerimos que su derivado,\( f′(x),\) sea continuo. Funciones como esta, que tienen derivadas continuas, se llaman lisas. (Esta propiedad vuelve a aparecer en capítulos posteriores.)

Dejar\( f(x)\) ser una función suave definida sobre\( [a,b]\). Queremos calcular la longitud de la curva desde el punto\( (a,f(a))\) hasta el punto\( (b,f(b))\). Comenzamos usando segmentos de línea para aproximar la longitud de la curva. Para\( i=0,1,2,…,n\), dejar\( P={x_i}\) ser una partición regular de\( [a,b]\). Después, para\( i=1,2,…,n\), construya un segmento de línea desde el punto\( (x_{i−1},f(x_{i−1}))\) hasta el punto\( (x_i,f(x_i))\). Aunque pueda parecer lógico usar segmentos de línea horizontales o verticales, queremos que nuestros segmentos de línea se aproximen lo más posible a la curva. La figura\(\PageIndex{1}\) representa este constructo para\( n=5\).

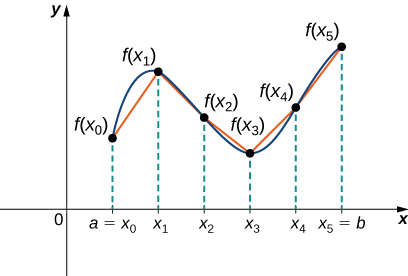
Esta figura es una gráfica en el primer cuadrante. La curva aumenta y disminuye. Se divide en partes en los puntos a=xsub0, xsub1, xsub2, xsub3, xsub4 y xsub5=b Además, hay segmentos de línea entre los puntos de la curva. — Figura\(\PageIndex{1}\): Podemos aproximar la longitud de una curva sumando segmentos de línea.

Para ayudarnos a encontrar la longitud de cada segmento de línea, observamos el cambio en la distancia vertical así como el cambio en la distancia horizontal en cada intervalo. Debido a que hemos utilizado una partición regular, el cambio en la distancia horizontal sobre cada intervalo viene dado por\( Δx\). Sin embargo, el cambio en la distancia vertical varía de un intervalo a otro, por lo que usamos\( Δy_i=f(x_i)−f(x_{i−1})\) para representar el cambio en la distancia vertical a lo largo del intervalo\( [x_{i−1},x_i]\), como se muestra en la Figura\(\PageIndex{2}\). Tenga en cuenta que algunos (o todos)\( Δy_i\) pueden ser negativos.

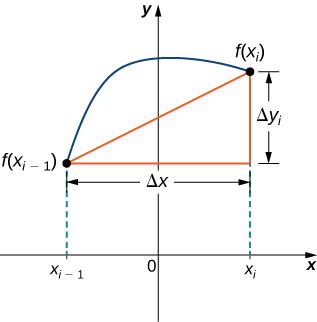
Esta figura es una gráfica. Es una curva por encima del eje x que comienza en el punto f (xsubi-1). La curva termina en el primer cuadrante en el punto f (xsubi). Entre los dos puntos de la curva hay un segmento de línea. Se forma un triángulo rectángulo con este segmento lineal como hipotenusa, un segmento horizontal con longitud delta x, y un segmento lineal vertical con longitud delta y. — Figura\(\PageIndex{2}\): Un segmento de línea representativo se aproxima a la curva a lo largo del intervalo\( [x_{i−1},x_i].\)

Según el teorema de Pitágoras, la longitud del segmento de línea es

\[ \sqrt{(Δx)^2+(Δy_i)^2}. \nonumber \]

También podemos escribir esto como

\[ Δx\sqrt{1+((Δy_i)/(Δx))^2}. \nonumber \]

Ahora bien, por el Teorema del Valor Medio, hay un punto\( x^∗_i∈[x_{i−1},x_i]\) tal que\( f′(x^∗_i)=(Δy_i)/(Δx)\). Luego, la longitud del segmento de línea viene dada por

\[ Δx\sqrt{1+[f′(x^∗_i)]^2}. \nonumber \]

Sumando las longitudes de todos los segmentos de línea, obtenemos

\[\text{Arc Length} ≈\sum_{i=1}^n\sqrt{1+[f′(x^∗_i)]^2}Δx.\nonumber \]

Se trata de una suma de Riemann. Tomando el límite como\( n→∞,\) tenemos

\[\begin{align*} \text{Arc Length} &=\lim_{n→∞}\sum_{i=1}^n\sqrt{1+[f′(x^∗_i)]^2}Δx \\[4pt] &=∫^b_a\sqrt{1+[f′(x)]^2}dx.\end{align*}\]

Resumimos estos hallazgos en el siguiente teorema.

Longitud de arco para\( y = f(x)\)

Dejar\( f(x)\) ser una función suave sobre el intervalo\([a,b]\). Entonces la longitud del arco de la porción de la gráfica de\( f(x)\) desde el punto\( (a,f(a))\) hasta el punto\( (b,f(b))\) viene dada por

\[\text{Arc Length}=∫^b_a\sqrt{1+[f′(x)]^2}\,dx. \nonumber \]

Tenga en cuenta que estamos integrando una expresión implicando\( f′(x)\), por lo que necesitamos estar seguros de que\( f′(x)\) es integrable. Es por ello que requerimos\( f(x)\) ser suaves. El siguiente ejemplo muestra cómo aplicar el teorema.

Ejemplo\( \PageIndex{1}\): Calculating the Arc Length of a Function of x

Vamos\( f(x)=2x^{3/2}\). Calcular la longitud del arco de la gráfica de\( f(x)\) sobre el intervalo\( [0,1]\). Redondear la respuesta a tres decimales.

Solución

Tenemos\( f′(x)=3x^{1/2},\) así\( [f′(x)]^2=9x.\) Entonces, la longitud del arco es

\[\begin{align*} \text{Arc Length} &=∫^b_a\sqrt{1+[f′(x)]^2}dx \nonumber \\[4pt] &= ∫^1_0\sqrt{1+9x}dx. \nonumber \end{align*}\]

Sustituir\( u=1+9x.\) Entonces,\( du=9dx.\) Cuando\( x=0\), entonces\( u=1\), y cuando\( x=1\), entonces\( u=10\). Por lo tanto,

\[ \begin{align*} \text{Arc Length} &=∫^1_0\sqrt{1+9x}dx \\[4pt] =\dfrac{1}{9}∫^1_0\sqrt{1+9x}9dx \\[4pt] &= \dfrac{1}{9}∫^{10}_1\sqrt{u}du \\[4pt] &=\dfrac{1}{9}⋅\dfrac{2}{3}u^{3/2}∣^{10}_1 =\dfrac{2}{27}[10\sqrt{10}−1] \\[4pt] &≈2.268units. \end{align*}\]

Ejercicio\(\PageIndex{1}\)

Vamos\(f(x)=(4/3)x^{3/2}\). Calcular la longitud del arco de la gráfica de\( f(x)\) sobre el intervalo\( [0,1]\). Redondear la respuesta a tres decimales.

Pista: Utilice el proceso del ejemplo anterior. No olvides cambiar los límites de la integración.

Responder: \[ \dfrac{1}{6}(5\sqrt{5}−1)≈1.697 \nonumber \]

Aunque es agradable tener una fórmula para calcular la longitud del arco, este teorema en particular puede generar expresiones que son difíciles de integrar. Estudiamos algunas técnicas de integración en Introducción a las Técnicas de Integración. En algunos casos, es posible que tengamos que usar una computadora o calculadora para aproximar el valor de la integral.

Ejemplo\( \PageIndex{2}\): Using a Computer or Calculator to Determine the Arc Length of a Function of x

Vamos\( f(x)=x^2\). Calcular la longitud del arco de la gráfica de\( f(x)\) sobre el intervalo\( [1,3]\).

Solución

Tenemos\( f′(x)=2x,\) así\( [f′(x)]^2=4x^2.\) Entonces la longitud del arco viene dada por

\[\begin{align*} \text{Arc Length} &=∫^b_a\sqrt{1+[f′(x)]^2}\,dx \\[4pt] &=∫^3_1\sqrt{1+4x^2}\,dx. \end{align*}\]

Usando una computadora para aproximar el valor de esta integral, obtenemos

\[ ∫^3_1\sqrt{1+4x^2}\,dx ≈ 8.26815. \nonumber \]

Ejercicio\(\PageIndex{2}\)

Vamos\( f(x)=\sin x\). Calcular la longitud del arco de la gráfica de\( f(x)\) sobre el intervalo\( [0,π]\). Utilice una computadora o calculadora para aproximar el valor de la integral.

Pista: Utilice el proceso del ejemplo anterior.

Responder: \[ \text{Arc Length} ≈ 3.8202 \nonumber \]

Longitud de Arco de la Curva\(x = g(y)\)

Acabamos de ver cómo aproximar la longitud de una curva con segmentos de línea. Si queremos encontrar la longitud del arco de la gráfica de una función de\(y\), podemos repetir el mismo proceso, excepto que particionamos el eje y en lugar del eje x. La figura\(\PageIndex{3}\) muestra un segmento lineal representativo.

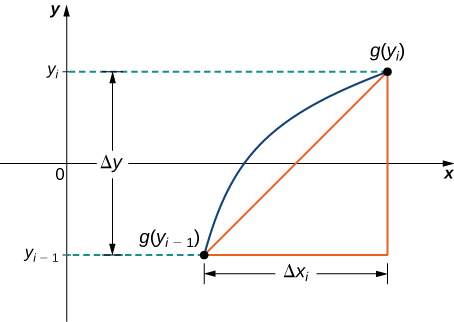
Esta figura es una gráfica. Es una curva a la derecha del eje y que comienza en el punto g (ysubi-1). La curva termina en el primer cuadrante en el punto g (ysubi). Entre los dos puntos de la curva hay un segmento de línea. Se forma un triángulo rectángulo con este segmento lineal como hipotenusa, un segmento horizontal con longitud delta x, y un segmento lineal vertical con longitud delta y. — Figura\(\PageIndex{3}\): Un segmento de línea representativo a lo largo del intervalo\([y_{i−1},y_i].\)

Entonces la longitud del segmento de línea es

\[\sqrt{(Δy)^2+(Δx_i)^2}, \nonumber \]

que también se puede escribir como

\[Δy\sqrt{1+\left(\dfrac{Δx_i}{Δy}\right)^2}. \nonumber \]

Si ahora seguimos el mismo desarrollo que hicimos antes, obtenemos una fórmula para la longitud del arco de una función\(x=g(y)\).

Longitud de Arco para x = g (y)

Dejar\(g(y)\) ser una función suave a lo largo de un intervalo\([c,d]\). Luego, la longitud del arco de la gráfica de\(g(y)\) desde el punto\((c,g(c))\) hasta el punto\((d,g(d))\) viene dada por

\[\text{Arc Length}=∫^d_c\sqrt{1+[g′(y)]^2}dy. \nonumber \]

Ejemplo\(\PageIndex{3}\): Calculating the Arc Length of a Function of \(y\)

Dejar\(g(y)=3y^3.\) Calcular la longitud del arco de la gráfica de\(g(y)\) sobre el intervalo\([1,2]\).

Solución

Tenemos\(g′(y)=9y^2,\) así\([g′(y)]^2=81y^4.\) Entonces la longitud del arco es

\[\begin{align*} \text{Arc Length} &=∫^d_c\sqrt{1+[g′(y)]^2}dy \\[4pt] &=∫^2_1\sqrt{1+81y^4}dy.\end{align*}\]

Usando una computadora para aproximar el valor de esta integral, obtenemos

\[ ∫^2_1\sqrt{1+81y^4}dy≈21.0277.\nonumber \]

Ejercicio\(\PageIndex{3}\)

Vamos\(g(y)=1/y\). Calcular la longitud del arco de la gráfica de\(g(y)\) sobre el intervalo\([1,4]\). Utilice una computadora o calculadora para aproximar el valor de la integral.

Pista: Utilice el proceso del ejemplo anterior.

Responder: \[\text{Arc Length} =3.15018 \nonumber \]

Área de una superficie de revolución

Los conceptos que utilizamos para encontrar la longitud del arco de una curva se pueden extender para encontrar el área superficial de una superficie de revolución. El área superficial es el área total de la capa exterior de un objeto. Para objetos como cubos o ladrillos, el área de superficie del objeto es la suma de las áreas de todas sus caras. Para superficies curvas, la situación es un poco más compleja. Dejar\(f(x)\) ser una función suave no negativa a lo largo del intervalo\([a,b]\). Deseamos encontrar el área superficial de la superficie de revolución creada al girar la gráfica\(y=f(x)\) alrededor del\(x\) eje -como se muestra en la siguiente figura.

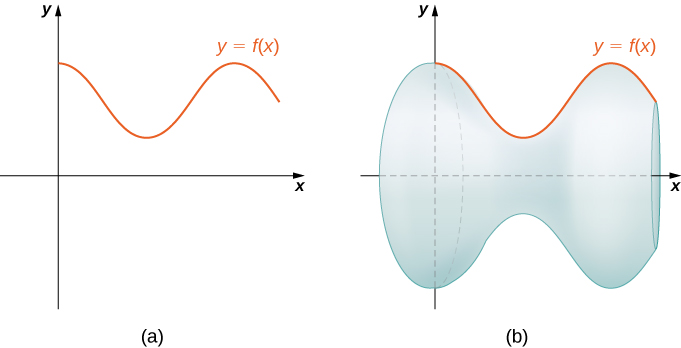
Esta figura tiene dos gráficas. La primera gráfica está etiquetada como “a” y es una curva en el primer cuadrante que comienza en el eje y. La curva es y=f (x). La segunda gráfica está etiquetada como “b” y tiene la misma curva y=f (x). También hay una superficie sólida formada por la rotación de la curva alrededor del eje x. — Figura\(\PageIndex{4}\): (a) Una curva que representa la función\(f(x)\). (b) La superficie de revolución formada al girar la gráfica de\(f(x)\) alrededor del\(x-axis\).

Como lo hemos hecho muchas veces antes, vamos a dividir el intervalo\([a,b]\) y aproximar el área de superficie calculando el área superficial de formas más simples. Comenzamos usando segmentos de línea para aproximar la curva, como hicimos anteriormente en esta sección. Para\(i=0,1,2,…,n\), dejar\(P={x_i}\) ser una partición regular de\([a,b]\). Después, para\(i=1,2,…,n,\) construir un segmento de línea desde el punto\((x_{i−1},f(x_{i−1}))\) hasta el punto\((x_i,f(x_i))\). Ahora, gire estos segmentos de línea alrededor del\(x\) eje -eje para generar una aproximación de la superficie de revolución como se muestra en la siguiente figura.

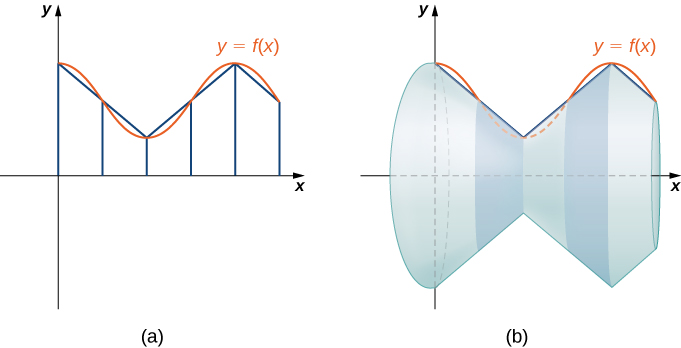
Observe que cuando cada segmento de línea gira alrededor del eje, produce una banda. Estas bandas son en realidad trozos de conos (piense en un cono de helado con el extremo puntizado cortado). Un trozo de cono como este se llama troncocono.

Para encontrar el área superficial de la banda, necesitamos encontrar el área de superficie lateral\(S\),, del tronco (el área de solo la superficie exterior inclinada del tronco, sin incluir las áreas de las caras superior o inferior). Dejar\(r_1\) y\(r_2\) ser los radios del extremo ancho y el extremo estrecho del tronco, respectivamente, y dejar\(l\) ser la altura inclinada del tronco como se muestra en la siguiente figura.

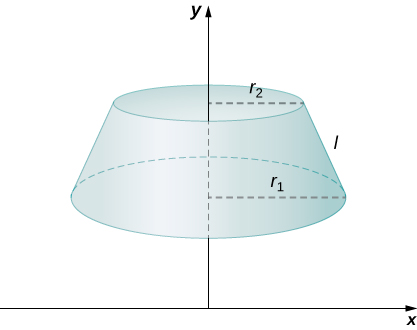
Esta figura es una gráfica. Es un cono troncocónico por encima del eje x con el eje y en el centro. El radio de la parte inferior del cono troncocónico es rsub1 y el radio de la parte superior es rsub2. La longitud del lado está etiquetada con “l”. — Figura\(\PageIndex{6}\): Un frustum de un cono puede aproximarse a una pequeña parte del área superficial.

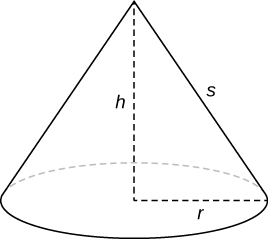
Sabemos que la superficie lateral de un cono viene dada por

\[\text{Lateral Surface Area } =πrs, \nonumber \]

donde\(r\) es el radio de la base del cono y\(s\) es la altura inclinada (Figura\(\PageIndex{7}\)).

Esta cifra es un cono. El cono tiene radio r, altura h y longitud del lado s. — Figura\(\PageIndex{7}\): La superficie lateral del cono viene dada por\(πrs\).

Dado que un tronco puede considerarse como un trozo de cono, el área de superficie lateral del tronco viene dada por el área de superficie lateral de todo el cono menos el área de superficie lateral del cono más pequeño (la punta puntiforme) que se cortó (Figura\(\PageIndex{8}\)).

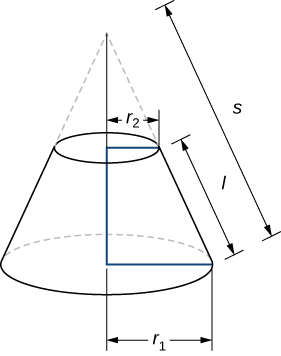
Esta figura es una gráfica. Es un frustum de cono. El radio de la parte inferior del cono troncocónico es rsub1 y el radio de la parte superior es rsub2. La longitud del lado está etiquetada con “l”. También está la parte superior de un cono con líneas discontinuas sobre el troncopo. Tiene longitud de lado s. — Figura\(\PageIndex{8}\): Cálculo del área de superficie lateral de un cono troncocónico.

Las secciones transversales del cono pequeño y el cono grande son triángulos similares, así vemos que

\[ \dfrac{r_2}{r_1}=\dfrac{s−l}{s} \nonumber \]

Resolviendo para\(s\), obtenemos =s−ls

\[\begin{align*} \dfrac{r_2}{r_1} &=\dfrac{s−l}{s} \\ r_2s &=r_1(s−l) \\ r_2s &=r_1s−r_1l \\ r_1l &=r_1s−r_2s \\ r_1l &=(r_1−r_2)s \\ \dfrac{r_1l}{r_1−r_2} =s \end{align*}\]

Entonces el área de superficie lateral (SA) del frustum es

\[\begin{align*} S &= \text{(Lateral SA of large cone)}− \text{(Lateral SA of small cone)} \\[4pt] &=πr_1s−πr_2(s−l) \\[4pt] &=πr_1(\dfrac{r_1l}{r_1−r_2})−πr_2(\dfrac{r_1l}{r_1−r_2−l}) \\[4pt] &=\dfrac{πr^2_1l}{r^1−r^2}−\dfrac{πr_1r_2l}{r_1−r_2}+πr_2l \\[4pt] &=\dfrac{πr^2_1l}{r_1−r_2}−\dfrac{πr_1r2_l}{r_1−r_2}+\dfrac{πr_2l(r_1−r_2)}{r_1−r_2} \\[4pt] &=\dfrac{πr^2_1}{lr_1−r_2}−\dfrac{πr_1r_2l}{r_1−r_2} + \dfrac{πr_1r_2l}{r_1−r_2}−\dfrac{πr^2_2l}{r_1−r_3} \\[4pt] &=\dfrac{π(r^2_1−r^2_2)l}{r_1−r_2}=\dfrac{π(r_1−r+2)(r1+r2)l}{r_1−r_2} \\[4pt] &= π(r_1+r_2)l. \label{eq20} \end{align*} \]

Ahora usemos esta fórmula para calcular el área de superficie de cada una de las bandas formadas girando los segmentos de línea alrededor de la\(x-axis\). En la siguiente figura se muestra una banda representativa.

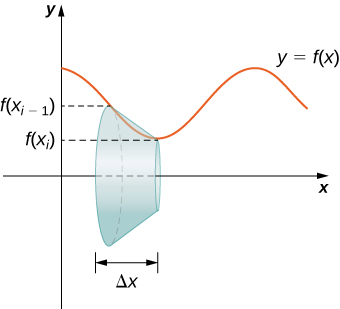
Esta figura tiene dos gráficos. El primero es una curva en el primer cuadrante. Alrededor del eje x hay un cono troncocónico. El borde del frustum está contra la curva. El borde comienza en f (xsubi-1) y termina en f (xsubi). La segunda imagen es la misma curva con el mismo tronco. La altura del tronco es delta x y la curva se etiqueta y=f (x). — Figura\(\PageIndex{9}\): Banda representativa utilizada para determinar el área superficial.

Tenga en cuenta que la altura inclinada de este tronco es solo la longitud del segmento de línea utilizado para generarlo. Entonces, aplicando la fórmula de superficie, tenemos

\[\begin{align*} S &=π(r_1+r_2)l \\ &=π(f(x_{i−1})+f(x_i))\sqrt{Δx^2+(Δyi)^2} \\ &=π(f(x_{i−1})+f(x_i))Δx\sqrt{1+(\dfrac{Δy_i}{Δx})^2} \end{align*}\]

Ahora, como hicimos en el desarrollo de la fórmula de longitud de arco, aplicamos el Teorema del Valor Medio para seleccionar\(x^∗_i∈[x_{i−1},x_i]\) tal que\(f′(x^∗_i)=(Δy_i)/Δx.\) Esto nos da

\[S=π(f(x_{i−1})+f(x_i))Δx\sqrt{1+(f′(x^∗_i))^2} \nonumber \]

Además, dado que\(f(x)\) es continuo, por el Teorema del Valor Intermedio, hay un punto\(x^{**}_i∈[x_{i−1},x[i]\) tal que\ (f (x^ {**} _i) =( 1/2) [f (xi−1) +f (xi)],

por lo que conseguimos

\[S=2πf(x^{**}_i)Δx\sqrt{1+(f′(x^∗_i))^2}.\nonumber \]

Luego, la superficie aproximada de toda la superficie de revolución viene dada por

\[\text{Surface Area} ≈\sum_{i=1}^n2πf(x^{**}_i)Δx\sqrt{1+(f′(x^∗_i))^2}.\nonumber \]

Esto casi parece una suma de Riemann, excepto que tenemos funciones evaluadas en dos puntos diferentes,\(x^∗_i\) y\(x^{**}_{i}\), a lo largo del intervalo\([x_{i−1},x_i]\). A pesar de que aquí no examinamos los detalles, resulta que porque\(f(x)\) es suave, si dejamos n\(→∞\), el límite funciona igual que una suma de Riemann incluso con los dos puntos de evaluación diferentes. Esto tiene sentido intuitivamente. Ambos\(x^∗_i\) y x^ {**} _i\) están en el intervalo\([x_{i−1},x_i]\), por lo que tiene sentido que como\(n→∞\), ambos\(x^∗_i\) y se\(x^{**}_i\) acerquen\(x\) Aquellos de ustedes que estén interesados en los detalles deben consultar un texto de cálculo avanzado.

Tomando el límite a medida\(n→∞,\) que obtenemos

\[ \begin{align*} \text{Surface Area} &=\lim_{n→∞}\sum_{i=1}n^2πf(x^{**}_i)Δx\sqrt{1+(f′(x^∗_i))^2} \\[4pt] &=∫^b_a(2πf(x)\sqrt{1+(f′(x))^2}) \end{align*}\]

Al igual que con la longitud del arco, podemos llevar\(y\) a cabo un desarrollo similar para las funciones de obtener una fórmula para el área superficial de las superficies de revolución sobre el\(y-axis\). Estos hallazgos se resumen en el siguiente teorema.

Superficie de una superficie de revolución

Dejar\(f(x)\) ser una función suave no negativa a lo largo del intervalo\([a,b]\). Luego, el área superficial de la superficie de revolución formada al girar la gráfica de\(f(x)\) alrededor del eje x viene dada por

\[\text{Surface Area}=∫^b_a(2πf(x)\sqrt{1+(f′(x))^2})dx \nonumber \]

Del mismo modo, deja\(g(y)\) ser una función suave no negativa a lo largo del intervalo\([c,d]\). Luego, el área superficial de la superficie de revolución formada al girar la gráfica de\(g(y)\) alrededor de la\(y-axis\) viene dada por

\[\text{Surface Area}=∫^d_c(2πg(y)\sqrt{1+(g′(y))^2}dy \nonumber \]

Ejemplo\(\PageIndex{4}\): Calculating the Surface Area of a Surface of Revolution 1.

Dejar\(f(x)=\sqrt{x}\) pasar el intervalo\([1,4]\). Encuentra el área de superficie de la superficie generada al girar la gráfica\(f(x)\) alrededor del\(x\) eje. Redondear la respuesta a tres decimales.

Solución

La gráfica\(f(x)\) y la superficie de rotación se muestran en la Figura\(\PageIndex{10}\).

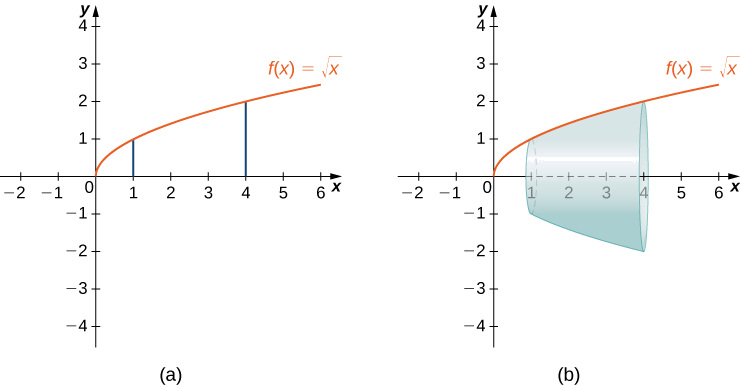
Esta figura tiene dos gráficas. El primero es la curva f (x) =squareroot (x). La curva va en aumento y comienza en el origen. También en la gráfica están las líneas verticales x=1 y x=4. La segunda gráfica es la misma función que la primera gráfica. La región entre f (x) y el eje x, delimitada por x=1 y x=4, se ha girado alrededor del eje x para formar una superficie. — Figura\(\PageIndex{10}\): (a) La gráfica de\(f(x)\). b) La superficie de la revolución.

Tenemos\(f(x)=\sqrt{x}\). Entonces,\(f′(x)=1/(2\sqrt{x})\) y\((f′(x))^2=1/(4x).\) Entonces,

\[\begin{align*} \text{Surface Area} &=∫^b_a(2πf(x)\sqrt{1+(f′(x))^2}dx \\[4pt] &=∫^4_1(\sqrt{2π\sqrt{x}1+\dfrac{1}{4x}})dx \\[4pt] &=∫^4_1(2π\sqrt{x+14}dx. \end{align*}\]

Vamos\(u=x+1/4.\) Entonces,\(du=dx\). Cuando\(x=1, u=5/4\), y cuando\(x=4, u=17/4.\) Esto nos da

\[\begin{align*} ∫^1_0(2π\sqrt{x+\dfrac{1}{4}})dx &= ∫^{17/4}_{5/4}2π\sqrt{u}du \\[4pt] &= 2π\left[\dfrac{2}{3}u^{3/2}\right]∣^{17/4}_{5/4} \\[4pt] &=\dfrac{π}{6}[17\sqrt{17}−5\sqrt{5}]≈30.846 \end{align*}\]

Ejercicio\(\PageIndex{4}\)

Dejar\( f(x)=\sqrt{1−x}\) pasar el intervalo\( [0,1/2]\). Encuentra el área de superficie de la superficie generada al girar la gráfica\( f(x)\) alrededor del\(x\) eje. Redondear la respuesta a tres decimales.

Pista: Utilice el proceso del ejemplo anterior.

Responder: \[ \dfrac{π}{6}(5\sqrt{5}−3\sqrt{3})≈3.133 \nonumber \]

Ejemplo\( \PageIndex{5}\): Calculating the Surface Area of a Surface of Revolution 2

Vamos\( f(x)=y=\dfrac[3]{3x}\). Considera la porción de la curva donde\( 0≤y≤2\). Encuentra el área de superficie de la superficie generada al girar la gráfica\( f(x)\) alrededor del\( y\) eje.

Solución

Observe que estamos girando la curva alrededor del\( y\) eje -eje, y el intervalo es en términos de\( y\), por lo que queremos reescribir la función como una función de\( y\). Obtenemos\( x=g(y)=(1/3)y^3\). La gráfica\( g(y)\) y la superficie de rotación se muestran en la siguiente figura.

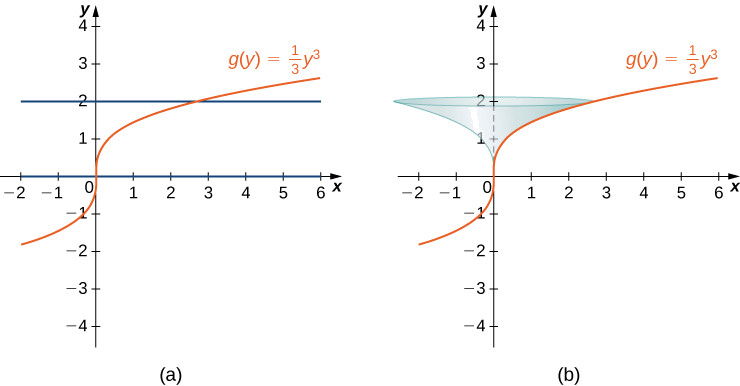
Esta figura tiene dos gráficas. El primero es la curva g (y) =1/3y^3. La curva va en aumento y comienza en el origen. También en la gráfica están las líneas horizontales y=0 e y=2. La segunda gráfica es la misma función que la primera gráfica. La región entre g (y) y el eje y, delimitada por y=0 e y=2, se ha girado alrededor del eje y para formar una superficie. — Figura\(\PageIndex{11}\): (a) La gráfica de\( g(y)\). b) La superficie de la revolución.

Tenemos\( g(y)=(1/3)y^3\), así\( g′(y)=y^2\) y\( (g′(y))^2=y^4\). Entonces

\[\begin{align*} \text{Surface Area} &=∫^d_c(2πg(y)\sqrt{1+(g′(y))^2})dy \\[4pt] &=∫^2_0(2π(\dfrac{1}{3}y^3)\sqrt{1+y^4})dy \\[4pt] &=\dfrac{2π}{3}∫^2_0(y^3\sqrt{1+y^4})dy. \end{align*}\]

Vamos\( u=y^4+1.\) Entonces\( du=4y^3dy\). Cuando\( y=0, u=1\), y cuando\( y=2, u=17.\) Entonces

\[\begin{align*} \dfrac{2π}{3}∫^2_0(y^3\sqrt{1+y^4})dy &=\dfrac{2π}{3}∫^{17}_1\dfrac{1}{4}\sqrt{u}du \\[4pt] &=\dfrac{π}{6}[\dfrac{2}{3}u^{3/2}]∣^{17}_1=\dfrac{π}{9}[(17)^{3/2}−1]≈24.118. \end{align*}\]

Ejercicio\(\PageIndex{5}\)

Dejar\( g(y)=\sqrt{9−y^2}\) pasar el intervalo\( y∈[0,2]\). Encuentra el área de superficie de la superficie generada al girar la gráfica\( g(y)\) alrededor del\( y\) eje.

Pista: Utilice el proceso del ejemplo anterior.

Responder: \( 12π\)

Conceptos clave

La longitud del arco de una curva se puede calcular usando una integral definida.
La longitud del arco se aproxima primero usando segmentos de línea, lo que genera una suma de Riemann. Tomar un límite entonces nos da la fórmula integral definitiva. El mismo proceso se puede aplicar a las funciones de\( y\).
Los conceptos utilizados para calcular la longitud del arco pueden generalizarse para encontrar el área superficial de una superficie de revolución.
Las integrales generadas por las fórmulas de longitud de arco y área de superficie suelen ser difíciles de evaluar. Puede ser necesario utilizar una computadora o calculadora para aproximar los valores de las integrales.

Ecuaciones Clave

Longitud de Arco de una Función de x

Longitud del arco\( =∫^b_a\sqrt{1+[f′(x)]^2}dx\)

Longitud de arco de una función de y

Longitud del arco\( =∫^d_c\sqrt{1+[g′(y)]^2}dy\)

Área de superficie de una función de x

Superficie\( =∫^b_a(2πf(x)\sqrt{1+(f′(x))^2})dx\)

Glosario

longitud del arco: la longitud del arco de una curva se puede considerar como la distancia que recorrería una persona a lo largo del camino de la curva

frustum: una porción de un cono; un tronco se construye cortando el cono con un plano paralelo a la base

superficie: el área superficial de un sólido es el área total de la capa exterior del objeto; para objetos como cubos o ladrillos, el área superficial del objeto es la suma de las áreas de todas sus caras