7.4E: Ejercicios para la Sección 7.4

Utilizar la descomposición parcial de la fracción (o una técnica más simple) para expresar la función racional como una suma o diferencia de dos o más expresiones racionales más simples.

1)\(\dfrac{1}{(x−3)(x−2)}\)

2)\(\dfrac{x^2+1}{x(x+1)(x+2)}\)

Contestar

\(\dfrac{x^2+1}{x(x+1)(x+2)} \quad = \quad −\dfrac{2}{x+1}+\dfrac{5}{2(x+2)}+\dfrac{1}{2x}\)

3)\(\dfrac{1}{x^3−x}\)

4)\(\dfrac{3x+1}{x^2}\)

Contestar

\(\dfrac{3x+1}{x^2} \quad = \quad \dfrac{1}{x^2}+\dfrac{3}{x}\)

5)\(\dfrac{3x^2}{x^2+1}\) (Pista: Utilice primero la división larga.)

6)\(\dfrac{2x^4}{x^2−2x}\)

Contestar

\(\dfrac{2x^4}{x^2−2x} \quad = \quad 2x^2+4x+8+\dfrac{16}{x−2}\)

7)\(\dfrac{1}{(x−1)(x^2+1)}\)

8)\(\dfrac{1}{x^2(x−1)}\)

Contestar

\(\dfrac{1}{x^2(x−1)} \quad = \quad −\dfrac{1}{x^2}−\dfrac{1}{x}+\dfrac{1}{x−1}\)

9)\(\dfrac{x}{x^2−4}\)

10)\(\dfrac{1}{x(x−1)(x−2)(x−3)}\)

Contestar

\(\dfrac{1}{x(x−1)(x−2)(x−3)} \quad = \quad −\dfrac{1}{2(x−2)}+\dfrac{1}{2(x−1)}−\dfrac{1}{6x}+\dfrac{1}{6(x−3)}\)

11)\(\dfrac{1}{x^4−1}=\dfrac{1}{(x+1)(x−1)(x^2+1)}\)

12)\(\dfrac{3x^2}{x^3−1}=\dfrac{3x^2}{(x−1)(x^2+x+1)}\)

Contestar

\(\dfrac{3x^2}{x^3−1} \quad = \quad \dfrac{1}{x−1}+\dfrac{2x+1}{x^2+x+1}\)

13)\(\dfrac{2x}{(x+2)^2}\)

14)\(\dfrac{3x^4+x^3+20x^2+3x+31}{(x+1)(x^2+4)^2}\)

Contestar

\(\dfrac{3x^4+x^3+20x^2+3x+31}{(x+1)(x^2+4)^2} \quad = \quad \dfrac{2}{x+1}+\dfrac{x}{x^2+4}−\dfrac{1}{(x^2+4)^2}\)

En los ejercicios 15 - 25, utilice el método de fracciones parciales para evaluar cada una de las siguientes integrales.

15)\(\displaystyle ∫\frac{dx}{(x−3)(x−2)}\)

16)\(\displaystyle ∫\frac{3x}{x^2+2x−8}\,dx\)

Contestar

\(\displaystyle ∫\frac{3x}{x^2+2x−8}\,dx \quad = \quad 2\ln|x+4|+\ln|x-2|+C = \ln\left| (x+4)^2(x-2) \right| + C\)

17)\(\displaystyle ∫\frac{dx}{x^3−x}\)

18)\(\displaystyle ∫\frac{x}{x^2−4}\,dx\)

Contestar

Ten en cuenta que aquí no necesitas Fracciones Parciales. Utilizamos una simple\(u\) -sustitución.
\(\displaystyle ∫\frac{x}{x^2−4}\,dx \quad = \quad \tfrac{1}{2}\ln|4−x^2|+C\)

19)\(\displaystyle ∫\frac{dx}{x(x−1)(x−2)(x−3)}\)

20)\(\displaystyle ∫\frac{2x^2+4x+22}{x^2+2x+10}\,dx\)

Contestar

Tenga en cuenta que dado que el grado del numerador es igual al grado del denominador, necesitamos comenzar con división larga.
Entonces tenga en cuenta que necesitaremos usar completar el cuadrado para continuar ya que no podemos facturar el trinomio en el denominador.
\(\displaystyle ∫\frac{2x^2+4x+22}{x^2+2x+10}\,dx \quad = \quad 2\left(x+\tfrac{1}{3}\arctan\left(\frac{1+x}{3}\right)\right)+C\)

21)\(\displaystyle ∫\frac{dx}{x^2−5x+6}\)

22)\(\displaystyle ∫\frac{2−x}{x^2+x}\,dx\)

Contestar

\(\displaystyle ∫\frac{2−x}{x^2+x}\,dx \quad = \quad 2\ln|x|−3\ln|1+x|+C = \ln\left| \frac{x^2}{(1+x)^3} \right|+C\)

23)\(\displaystyle ∫\frac{2}{x^2−x−6}\,dx\)

24)\(\displaystyle ∫\frac{dx}{x^3−2x^2−4x+8}\)

Contestar

\(\displaystyle ∫\frac{dx}{x^3−2x^2−4x+8} \quad = \quad \tfrac{1}{16}\left(−\frac{4}{−2+x}−\ln|−2+x|+\ln|2+x|\right)+C = \tfrac{1}{16}\left(−\frac{4}{−2+x}+\ln\left| \frac{x+2}{x-2} \right|\right)+C\)

25)\(\displaystyle ∫\frac{dx}{x^4−10x^2+9}\)

En los ejercicios 26 - 29, evaluar las integrales con factores cuadráticos irreducibles en los denominadores.

26)\(\displaystyle ∫\frac{2}{(x−4)(x^2+2x+6)}\,dx\)

Contestar

\(\displaystyle ∫\frac{2}{(x−4)(x^2+2x+6)}\,dx \quad = \quad \tfrac{1}{30}(−2\sqrt{5}\arctan\left[\frac{1+x}{\sqrt{5}}\right]+2\ln|−4+x|−\ln|6+2x+x^2|)+C\)

27)\(\displaystyle ∫\frac{x^2}{x^3−x^2+4x−4}\,dx\)

28)\(\displaystyle ∫\frac{x^3+6x^2+3x+6}{x^3+2x^2}\,dx\)

Contestar

Tenga en cuenta que necesitamos usar primero la división larga, ya que el grado del numerador es mayor que el grado del denominador.
\(\displaystyle ∫\frac{x^3+6x^2+3x+6}{x^3+2x^2}\,dx \quad = \quad −\frac{3}{x}+4\ln|x+2|+x+C\)

29)\(\displaystyle ∫\frac{x}{(x−1)(x^2+2x+2)^2}\,dx\)

En los ejercicios 30 - 32, utilice el método de fracciones parciales para evaluar las integrales.

30)\(\displaystyle ∫\frac{3x+4}{(x^2+4)(3−x)}\,dx\)

Contestar

\(\displaystyle ∫\frac{3x+4}{(x^2+4)(3−x)}\,dx \quad = \quad −\ln|3−x|+\tfrac{1}{2}\ln|x^2+4|+C\)

31)\(\displaystyle ∫\frac{2}{(x+2)^2(2−x)}\,dx\)

32)\(\displaystyle ∫\frac{3x+4}{x^3−2x−4}\,dx\) (Pista: Utilizar el teorema de raíz racional.)

Contestar

\(\displaystyle ∫\frac{3x+4}{x^3−2x−4}\,dx \quad = \quad \ln|x−2|−\tfrac{1}{2}\ln|x^2+2x+2|+C\)

En los ejercicios 33 - 46, utilice la sustitución para convertir las integrales en integrales de funciones racionales. Luego usa fracciones parciales para evaluar las integrales.

33)\(\displaystyle ∫^1_0\frac{e^x}{36−e^{2x}}\,dx\) (Dar la respuesta exacta y el equivalente decimal. Redondear a cinco decimales.)

34)\(\displaystyle ∫\frac{e^x\,dx}{e^{2x}−e^x}\,dx\)

Contestar

\(\displaystyle ∫\frac{e^x\,dx}{e^{2x}−e^x}\,dx \quad = \quad −x+\ln|1−e^x|+C\)

35)\(\displaystyle ∫\frac{\sin x\,dx}{1−\cos^2x}\)

36)\(\displaystyle ∫\frac{\sin x}{\cos^2 x+\cos x−6}\,dx\)

Contestar

\(\displaystyle ∫\frac{\sin x}{\cos^2 x+\cos x−6}\,dx \quad = \quad \tfrac{1}{5}\ln\left|\frac{\cos x+3}{\cos x−2}\right|+C\)

37)\(\displaystyle ∫\frac{1−\sqrt{x}}{1+\sqrt{x}}\,dx\)

38)\(\displaystyle ∫\frac{dt}{(e^t−e^{−t})^2}\)

Contestar

\(\displaystyle ∫\frac{dt}{(e^t−e^{−t})^2} \quad = \quad \frac{1}{2−2e^{2t}}+C\)

39)\(\displaystyle ∫\frac{1+e^x}{1−e^x}\,dx\)

40)\(\displaystyle ∫\frac{dx}{1+\sqrt{x+1}}\)

Contestar

\(\displaystyle ∫\frac{dx}{1+\sqrt{x+1}} \quad = \quad 2\sqrt{1+x}−2\ln|1+\sqrt{1+x}|+C\)

41)\(\displaystyle ∫\frac{dx}{\sqrt{x}+\sqrt[4]{x}}\)

42)\(\displaystyle ∫\frac{\cos x}{\sin x(1−\sin x)}\,dx\)

Contestar

\(\displaystyle ∫\frac{\cos x}{\sin x(1−\sin x)}\,dx \quad = \quad \ln\left|\frac{\sin x}{1−\sin x}\right|+C\)

43)\(\displaystyle ∫\frac{e^x}{(e^{2x}−4)^2}\,dx\)

44)\(\displaystyle ∫_1^2\frac{1}{x^2\sqrt{4−x^2}}\,dx\)

Contestar

\(\displaystyle ∫_1^2\frac{1}{x^2\sqrt{4−x^2}}\,dx \quad = \quad \frac{\sqrt{3}}{4}\)

45)\(\displaystyle ∫\frac{1}{2+e^{−x}}\,dx\)

46)\(\displaystyle ∫\frac{1}{1+e^x}\,dx\)

Contestar

\(\displaystyle ∫\frac{1}{1+e^x}\,dx \quad = \quad x−\ln(1+e^x)+C\)

En los ejercicios 47 - 48, utilizar la sustitución dada para convertir la integral en una integral de una función racional, luego evaluar.

47)\(\displaystyle ∫\frac{1}{t−\sqrt[3]{t}}\,dt; \quad t=x^3\)

48)\(\displaystyle ∫\frac{1}{\sqrt{x}+\sqrt[3]{x}}\,dx; \quad x=u^6\)

Contestar

\(\displaystyle ∫\frac{1}{\sqrt{x}+\sqrt[3]{x}}\,dx \quad = \quad 6x^{1/6}−3x^{1/3}+2\sqrt{x}−6\ln(1+x^{1/6})+C\)

49) Graficar la curva\(y=\dfrac{x}{1+x}\) a lo largo del intervalo\([0,5]\). Luego, busque el área de la región delimitada por la curva, el\(x\) eje -y la línea\(x=4\).

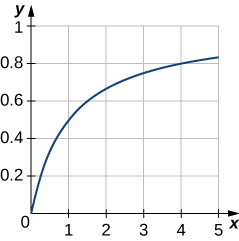
50) Encuentra el volumen del sólido generado cuando la región delimitada por\(y=\dfrac{1}{\sqrt{x(3−x)}}, \,y=0, \,x=1,\) y\(x=2\) gira alrededor del\(x\) eje -eje.

Contestar

\(V = \frac{4}{3}π\text{arctanh}\,\left[\frac{1}{3}\right]=\frac{1}{3}π\ln 4 \, \text{units}^3\)

51) La velocidad de una partícula que se mueve a lo largo de una línea es una función del tiempo dada por\(v(t)=\dfrac{88t^2}{t^2+1}.\) Encontrar la distancia que la partícula ha recorrido después del\(t=5\) sec.

En los ejercicios 52 - 54, resolver el problema del valor inicial para\(x\) en función de\(t\).

52)\((t^2−7t+12)\dfrac{dx}{dt}=1,\quad t>4,\, x(5)=0\)

Contestar

\( x=−\ln|t−3|+\ln|t−4|+\ln 2 = \ln\left| \dfrac{2(t-4)}{t-3}\right|\)

53)\((t+5)\dfrac{dx}{dt}=x^2+1, \quad t>−5,\,x(1)=\tan 1\)

54)\((2t^3−2t^2+t−1)\dfrac{dx}{dt}=3,\quad x(2)=0\)

Contestar

\(x=\ln|t−1|−\sqrt{2}\arctan(\sqrt{2}t)−\frac{1}{2}\ln(t^2+\frac{1}{2})+\sqrt{2}\arctan(2\sqrt{2})+\frac{1}{2}\ln 4.5\)

55) Encuentra la\(x\) coordenada -del centroide del área delimitada por\(y(x^2−9)=1, \, y=0, \,x=4,\) y\(x=5.\) (Redondear la respuesta a dos decimales.)

56) Encuentra el volumen generado al girar el área delimitada por\(y=\dfrac{1}{x^3+7x^2+6x},\, x=1,\, x=7\), y\(y=0\) alrededor del\(y\) eje.

Contestar

\(V = \frac{2}{5}π\ln\frac{28}{13} \, \text{units}^3\)

57) Encuentra el área delimitada por\(y=\dfrac{x−12}{x^2−8x−20}, \,y=0, \,x=2,\) y\(x=4\). (Redondear la respuesta a la centésima más cercana.)

58) Evaluar la integral\(\displaystyle ∫\frac{dx}{x^3+1}.\)

Contestar

\(\displaystyle ∫\frac{dx}{x^3+1} \quad = \quad \frac{\arctan[\frac{−1+2x}{\sqrt{3}}]}{\sqrt{3}}+\frac{1}{3}\ln|1+x|−\frac{1}{6}\ln∣1−x+x^2∣+C\)

Para problemas 59 - 62, use las sustituciones\(\tan(\frac{x}{2})=t, \,dx=\dfrac{2}{1+t^2}\,dt, \, \sin x=\dfrac{2t}{1+t^2},\) y\(\cos x=\dfrac{1−t^2}{1+t^2}.\)

59)\(\displaystyle ∫\frac{dx}{3−5\sin x}\)

60) Encuentra el área bajo la curva\(y=\dfrac{1}{1+\sin x}\) entre\(x=0\) y\(x=π.\) (Supongamos que las dimensiones están en pulgadas.)

Contestar

2.0 in. ²

61) Dado\(\tan\left(\frac{x}{2}\right)=t,\) derivar las fórmulas\(dx=\dfrac{2}{1+t^2}dt, \,\sin x=\dfrac{2t}{1+t^2}\), y\(\cos x=\dfrac{1−t^2}{1+t^2}.\)

62) Evaluar\(\displaystyle ∫\frac{\sqrt[3]{x−8}}{x}\,dx.\)

Contestar

\(\displaystyle ∫\frac{\sqrt[3]{x−8}}{x}\,dx \quad = \quad 3(−8+x)^{1/3}−2\sqrt{3}\arctan\left[\frac{−1+(−8+x)^{1/3}}{\sqrt{3}}\right]−2\ln\left[2+(−8+x)^{1/3}\right]+\ln\left[4−2(−8+x)^{1/3}+(−8+x)^{2/3}\right]+C\)