8.2: Campos de dirección y métodos numéricos
- Page ID
- 116274
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Dibuja el campo de dirección para una ecuación diferencial de primer orden dada.
- Utilice un campo de dirección para dibujar una curva de solución de una ecuación diferencial de primer orden.
- Utilice el Método de Euler para aproximar la solución a una ecuación diferencial de primer orden.
Para el resto de este capítulo nos centraremos en diversos métodos para resolver ecuaciones diferenciales y analizar el comportamiento de las soluciones. En algunos casos es posible predecir propiedades de una solución a una ecuación diferencial sin conocer la solución real. También estudiaremos métodos numéricos para resolver ecuaciones diferenciales, que se pueden programar usando diversos lenguajes informáticos o incluso mediante un programa de hoja de cálculo, como Microsoft Excel.
Creación de campos de dirección
Los campos de dirección (también llamados campos de pendiente) son útiles para investigar ecuaciones diferenciales de primer orden. En particular, consideramos una ecuación diferencial de primer orden de la forma
\[ y'=f(x,y).\nonumber \]
Un ejemplo aplicado de este tipo de ecuación diferencial aparece en la ley del enfriamiento de Newton, que resolveremos explícitamente más adelante en este capítulo. Primero, sin embargo, vamos a crear un campo de dirección para la ecuación diferencial
\[ T′(t)=−0.4(T−72).\nonumber \]
Aquí\( T(t)\) representa la temperatura (en grados Fahrenheit) de un objeto a la vez\( t\), y la temperatura ambiente es\( 72°F\). La figura\( \PageIndex{1}\) muestra el campo de dirección para esta ecuación.
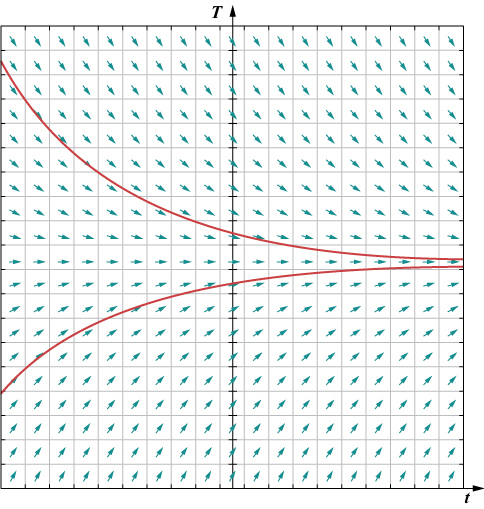
La idea detrás de un campo de dirección es el hecho de que la derivada de una función evaluada en un punto dado es la pendiente de la línea tangente a la gráfica de esa función en el mismo punto. Otros ejemplos de ecuaciones diferenciales para las que podemos crear un campo de dirección incluyen
\[ y'=3x+2y−4\nonumber \]
\[ y'=x^2−y^2\nonumber \]
\[ y'=\frac{2x+4}{y−2}.\nonumber \]
Para crear un campo de dirección, comenzamos con la primera ecuación:\( y'=3x+2y−4\). Dejamos\( \left(x_0,\, y_0\right)\) ser cualquier par ordenado, y sustituimos estos números en el lado derecho de la ecuación diferencial. Por ejemplo, si elegimos\( x=1\) y\( y=2\), sustituyendo en el lado derecho de la ecuación diferencial rinde
\( y′=3x+2y−4=3(1)+2(2)−4=3.\)
Esto nos dice que si una solución a la ecuación diferencial\( y'=3x+2y−4\) pasa por el punto\( (1,2)\), entonces la pendiente de la solución en ese punto debe ser igual a 3. Para comenzar a crear el campo de dirección, colocamos un segmento de línea corta en el punto\( (1,2)\) que tiene pendiente\( 3\). Podemos hacer esto para cualquier punto en el dominio de la función\( f(x,y)=3x+2y−4,\) que consiste en todos los pares ordenados\( (x,y)\) en\( R^2\). Por lo tanto, cualquier punto en el plano cartesiano tiene una pendiente asociada a él, asumiendo que una solución a la ecuación diferencial pasa por ese punto. El campo de dirección para la ecuación diferencial\( y′=3x+2y−4\) se muestra en la Figura\( \PageIndex{2}\).
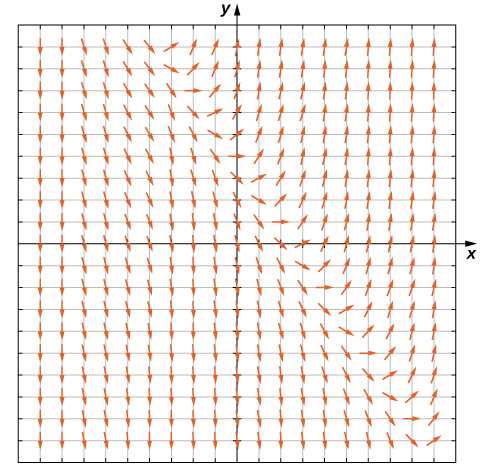
Podemos generar un campo de dirección de este tipo para cualquier ecuación diferencial de la forma\( y'=f(x,y).\)
Un campo de dirección (campo de pendiente) es un objeto matemático utilizado para representar gráficamente soluciones a una ecuación diferencial de primer orden. En cada punto de un campo de dirección, aparece un segmento de línea cuya pendiente es igual a la pendiente de una solución a la ecuación diferencial que pasa por ese punto.
Uso de campos de dirección
Podemos usar un campo de dirección para predecir el comportamiento de las soluciones a una ecuación diferencial sin conocer la solución real. Por ejemplo, el campo de dirección en la Figura\( \PageIndex{3}\) sirve como guía para el comportamiento de las soluciones a la ecuación diferencial\( y'=3x+2y−4.\)
Para usar un campo de dirección, comenzamos por elegir cualquier punto en el campo. El segmento de línea en ese punto sirve como señal indicándonos en qué dirección ir desde allí. Por ejemplo, si una solución a la ecuación diferencial pasa por el punto\( (0,1),\) entonces la pendiente de la solución que pasa por ese punto viene dada por\( y'=3(0)+2(1)−4=−2.\) Ahora vamos a\( x\) aumentar ligeramente, digamos a\( x=0.1\). El uso del método de aproximaciones lineales da una fórmula para el valor aproximado de\( y\) para\( x=0.1.\) En particular,
\[ L(x)=y_0+f′(x_0)(x−x_0)=1−2(x_0−0)=1−2x_0.\nonumber \]
Sustituir\( x_0=0.1\) en\( L(x)\) da un\( y\) valor aproximado de\( 0.8\).
En este punto la pendiente de la solución cambia (nuevamente según la ecuación diferencial). Podemos seguir progresando, recalculando la pendiente de la solución a medida que damos pequeños pasos hacia la derecha, y observando el comportamiento de la solución. La figura\( \PageIndex{3}\) muestra una gráfica de la solución que pasa por el punto\( (0,1)\).
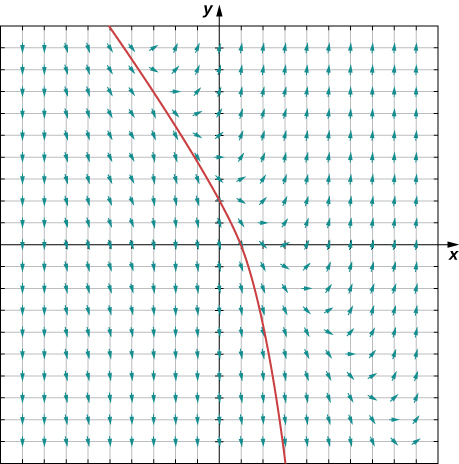
La curva es la gráfica de la solución al problema del valor inicial
\[ y'=3x+2y−4,\; y(0)=1.\nonumber \]
Esta curva se denomina curva de solución que pasa por el punto\( (0,1).\) La solución exacta a este problema de valor inicial es
\[ y=−\frac{3}{2}x+\frac{5}{4}−\frac{1}{4}e^{2x},\nonumber \]
y la gráfica de esta solución es idéntica a la curva de la Figura\( \PageIndex{3}\).
Cree un campo de dirección para la ecuación diferencial\( y'=x^2−y^2\) y esboce una curva de solución que pase por el punto\( (−1,2)\).
- Pista
-
Uso\( x\) y\( y\) valores que van desde\( −5\) hasta\( 5\). Para cada par de coordenadas, calcule\( y'\) usando el lado derecho de la ecuación diferencial.
- Responder
-
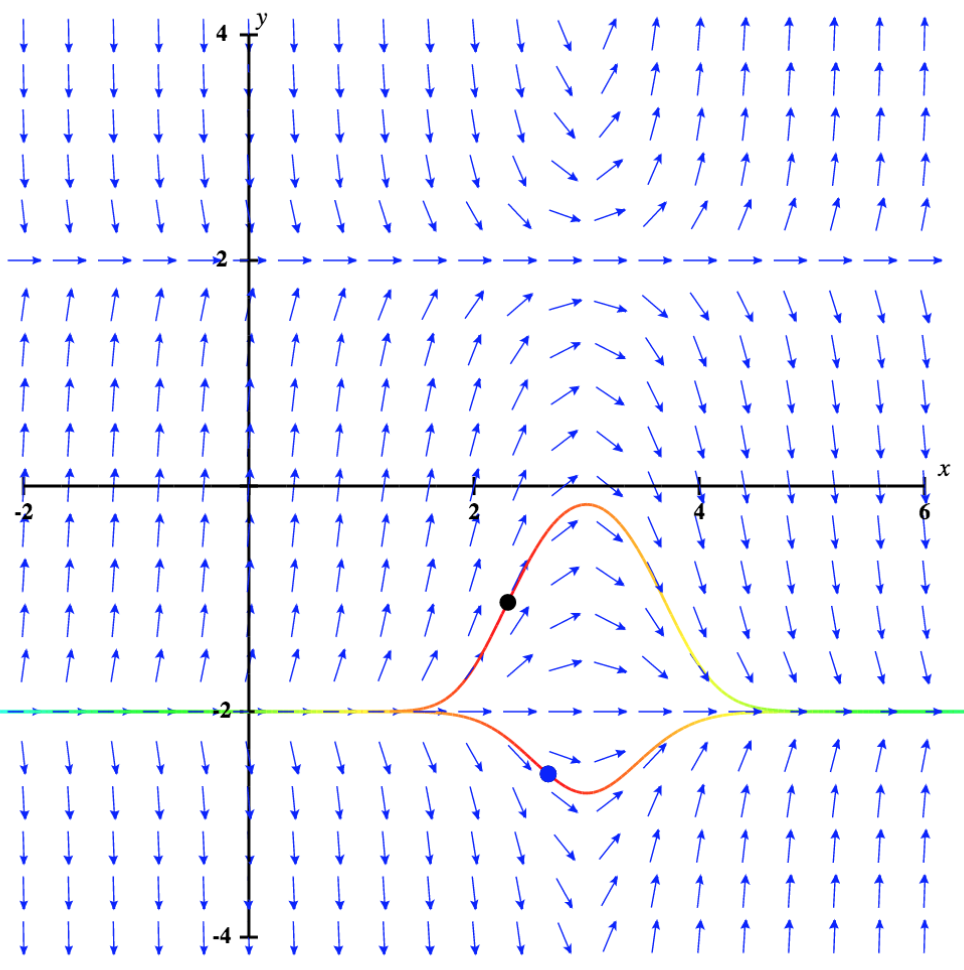
Ahora considere el campo de dirección para la ecuación diferencial\( y'=(x−3)(y^2−4)\), que se muestra en la Figura\( \PageIndex{4}\). Este campo de dirección tiene varias propiedades interesantes. En primer lugar, en\( y=−2\) y\( y=2\), aparecen guiones horizontales a lo largo de la gráfica. Esto significa que si\( y=−2\), entonces\( y'=0.\) Sustituir esta expresión en el lado derecho de la ecuación diferencial da
\ [\ begin {align*} (x−3) (y^2−4) &= (x−3) ((−2) ^2−4)\\ [4pt]
& =( x−3) (0)\\ [4pt]
&=0\\ [4pt]
&=y'. \ end {alinear*}\]
Por lo tanto,\( y=−2\) es una solución a la ecuación diferencial. De igual manera,\( y=2\) es una solución a la ecuación diferencial. Estas son las únicas soluciones de valor constante a la ecuación diferencial, como podemos ver en el siguiente argumento. Supongamos que\( y=k\) es una solución constante a la ecuación diferencial. Entonces\( y′=0\). Sustituir esta expresión en la ecuación diferencial rinde\( 0=(x−3)(k^2−4)\). Esta ecuación debe ser cierta para todos los valores de\( x\), por lo que el segundo factor debe ser igual a cero. Este resultado arroja la ecuación\( k^2−4=0\). Las soluciones a esta ecuación son\( k=−2\) y\( k=2\), que son las soluciones constantes ya mencionadas. A estas se les llama las soluciones de equilibrio a la ecuación diferencial.
Considera la ecuación diferencial\( y'=f(x,y)\). Una solución de equilibrio es cualquier solución a la ecuación diferencial de la forma\( y=c\), donde\(c\) es una constante.
Para determinar las soluciones de equilibrio a la ecuación diferencial\( y'=f(x,y)\), establezca el lado derecho igual a cero. Una solución de equilibrio de la ecuación diferencial es cualquier función de la forma\( y=k\) tal que\( f(x,k)=0\) para todos los valores de\( x\) en el dominio de\( f\).
Una característica importante de las soluciones de equilibrio se refiere a si se acercan o no a la línea\( y=k\) como una asíntota para grandes valores de\( x\).
Considere la ecuación diferencial\( y′=f(x,y),\) y asuma que todas las soluciones a esta ecuación diferencial están definidas para\( x≥x_0\). Dejar\( y=k\) ser una solución de equilibrio a la ecuación diferencial.
- \( y=k\)es una solución asintóticamente estable a la ecuación diferencial si existe\( ε>0\) tal que para cualquier valor\( c∈(k−ε,\, k+ε)\) la solución al problema del valor inicial se\( y′=f(x,y), \; y(x_0)=c\) aproxime a\( k\) medida que se\( x\) acerca al infinito.
- \( y=k\)es una solución asintóticamente inestable a la ecuación diferencial si existe\( ε>0\) tal que por cualquier valor\( c∈(k−ε,\, k+ε)\) la solución al problema del valor inicial\( y′=f(x,y), \; y(x_0)=c\) nunca se aproxima\( k\) como se\( x\) acerca al infinito.
- \( y=k\)es una solución asintóticamente semi-estable a la ecuación diferencial si no es asintóticamente estable ni asintóticamente inestable.
Ahora volvemos a la ecuación diferencial\( y'=(x−3)(y^2−4)\), con la condición inicial\( y(0)=0.5\). El campo de dirección para este problema de valor inicial, junto con la solución correspondiente, se muestra en la Figura\( \PageIndex{5}\).
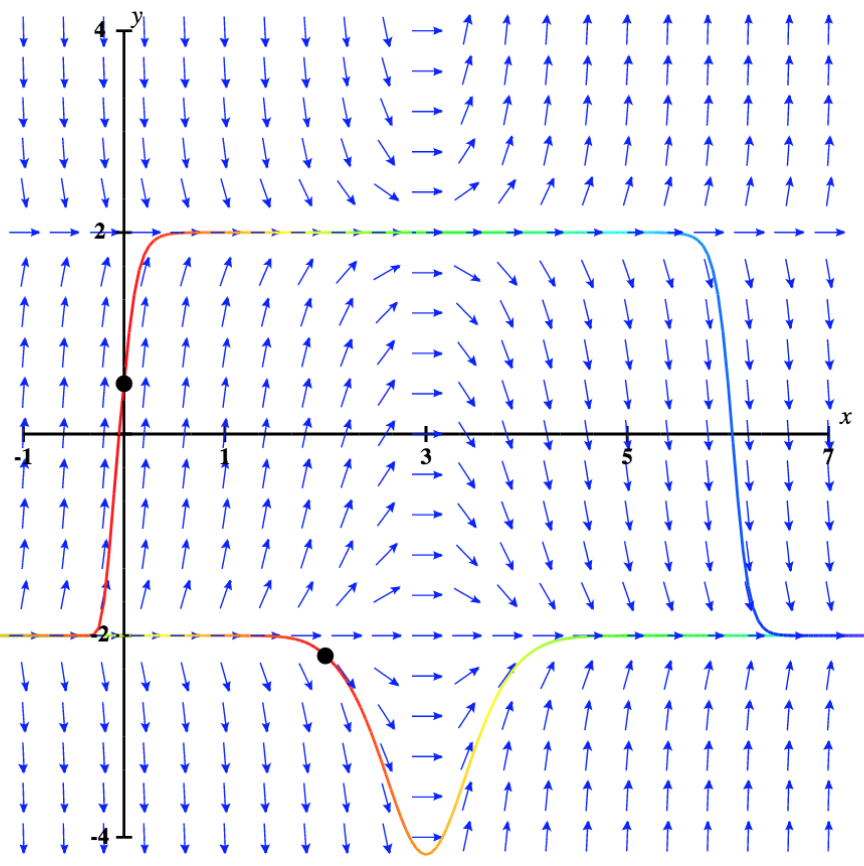
Los valores de la solución a este problema de valor inicial permanecen entre\( y=−2\) y\( y=2\), que son las soluciones de equilibrio a la ecuación diferencial. Además, a medida que\( x\) se acerca al infinito, aunque inicialmente parecen acercarse a la línea y = 2, las\( y\) coordenadas se acercan claramente\( -2\). El comportamiento de las soluciones es similar si el valor inicial está por debajo\( -2\), por ejemplo,\( y(2)=-2.2\). En este caso, las soluciones aumentan y se acercan a\( y=-2\) medida que se\( x\) acerca al infinito. Por lo tanto,\( y=-2\) es una solución asintóticamente estable a esta ecuación diferencial.
¿Qué sucede cuando el valor inicial está por encima\( y=2\)? Este escenario se ilustra en la Figura\( \PageIndex{6}\), con el valor inicial\( y(0)=3.\)
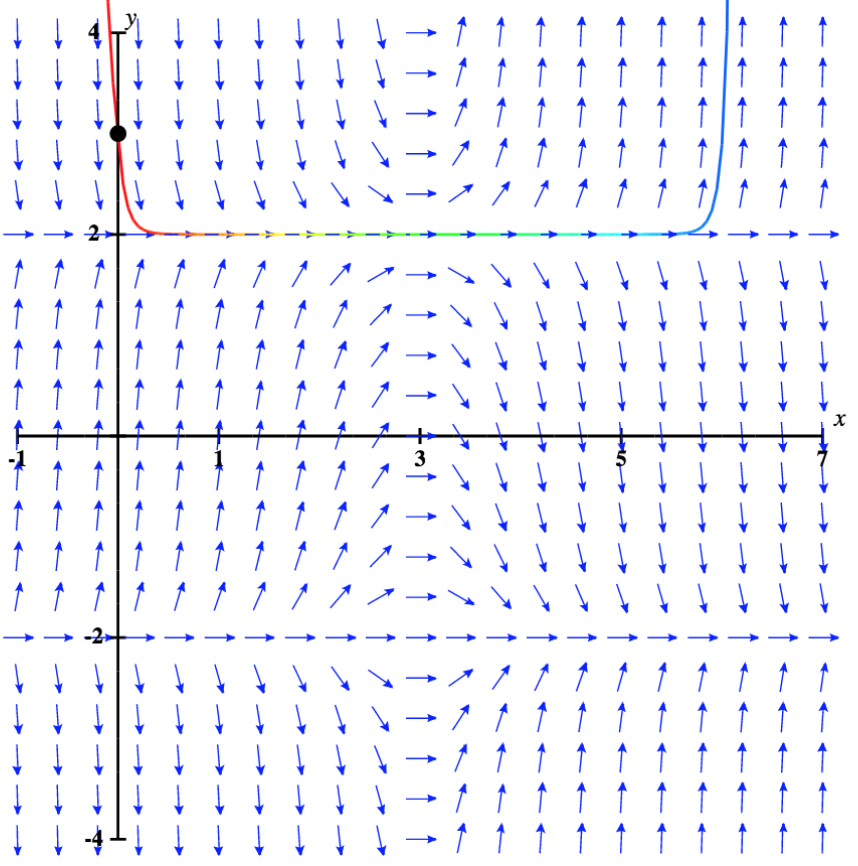
La solución aumenta rápidamente hacia el infinito positivo a medida que se\( x\) acerca al infinito. Además, si el valor inicial está ligeramente por debajo\( 2\), entonces la solución se acerca\( -2\), que es la otra solución de equilibrio. Por lo tanto, en ninguno de los casos se acerca la solución\( y=2\), así\( y=2\) se denomina solución asintóticamente inestable, o inestable, de equilibrio.
Crear un campo de dirección para la ecuación diferencial\( y'=(y−3)^2(y^2+y−2)\) e identificar cualquier solución de equilibrio. Clasificar cada una de las soluciones de equilibrio como estables, inestables o semiestables.
Solución
El campo de dirección se muestra en la Figura\( \PageIndex{7}\).
Las soluciones de equilibrio son\( y=−2,\, y=1,\) y\( y=3\). Para clasificar cada una de las soluciones, mira una flecha directamente encima o debajo de cada uno de estos valores. Por ejemplo, en\( y=−2\) las flechas directamente debajo de esta solución apuntan hacia arriba, y las flechas directamente encima de la solución apuntan hacia abajo. Por lo tanto, todas las condiciones iniciales se\( y=−2\) acercan\( y=−2\), y la solución es estable. Para la solución\( y=1\), todas las condiciones iniciales arriba y abajo\( y=1\) son repelidas (alejadas) de\( y=1\), por lo que esta solución es inestable. La solución\( y=3\) es semiestable, ya que para condiciones iniciales ligeramente mayores que\( 3\), la solución se aproxima al infinito, y para condiciones iniciales ligeramente menores que\( 3\), la solución se aproxima\( y=1\).
Análisis
Es posible encontrar las soluciones de equilibrio a la ecuación diferencial estableciendo el lado derecho igual a cero y resolviendo para\( y.\) Este enfoque da las mismas soluciones de equilibrio que las que vimos en el campo de dirección.
Crear un campo de dirección para la ecuación diferencial\( y'=(x+5)(y+2)(y^2−4y+4)\) e identificar cualquier solución de equilibrio. Clasificar cada una de las soluciones de equilibrio como estables, inestables o semiestables.
- Pista
-
Primero crea el campo de dirección y busca guiones horizontales que crucen todo el camino. Luego examine las líneas de pendiente directamente por encima y por debajo de las soluciones de equilibrio.
- Responder
-
Las soluciones de equilibrio son\( y=−2\) y\( y=2\). Para esta ecuación,\( y=−2\) es una solución de equilibrio inestable, y\( y=2\) es una solución de equilibrio semiestable.
-4 y hacia abajo para y < -4. Cerca de y = 4, las flechas son más horizontales, pero cuanto más alejadas, más verticales se vuelven." src="https://math.libretexts.org/@api/dek...2452/8.2.3.png">
Método de Euler
Considere el problema del valor inicial
\[ y′=2x−3,\;y(0)=3.\nonumber \]
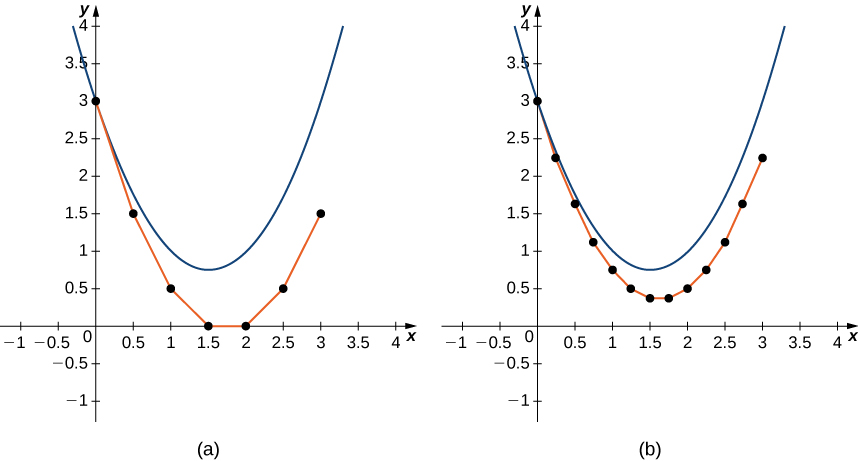
Integrando ambos lados de la ecuación diferencial da\( y=x^2−3x+C,\) y resolviendo para\( C\) rendimientos la solución particular\( y=x^2−3x+3.\) La solución para este problema de valor inicial aparece como la parábola en la Figura\( \PageIndex{8}\).
![Una gráfica sobre el rango [-1,4] para x e y. La parábola de apertura hacia arriba dada se dibuja con vértice en (1.5, 0.75). Los puntos individuales se trazan en (0, 3), (0.5, 1.5), (1, 0.5), (1.5, 0), (2, 0), (2.5, 0.5) y (3, 1.5) con segmentos de línea que los conectan.](https://math.libretexts.org/@api/deki/files/2916/CNX_Calc_Figure_08_02_010.jpeg)
El gráfico rojo consiste en segmentos de línea que se aproximan a la solución al problema del valor inicial. La gráfica comienza en el mismo valor inicial de\( (0,3)\). Entonces la pendiente de la solución en cualquier punto es determinada por el lado derecho de la ecuación diferencial, y la longitud del segmento de línea se determina aumentando el\( x\) valor por\( 0.5\) cada vez (el tamaño del paso). Este enfoque es la base del Método de Euler.
Antes de declarar el Método de Euler como teorema, consideremos otro problema de valor inicial:
\[ y′=x^2−y^2,\; y(−1)=2.\nonumber \]
La idea detrás de los campos de dirección también se puede aplicar a este problema para estudiar el comportamiento de su solución. Por ejemplo, en el punto\( (−1,2),\) la pendiente de la solución viene dada por\( y'=(−1)^2−2^2=−3\), por lo que la pendiente de la línea tangente a la solución en ese punto también es igual a\( −3\). Ahora definimos\( x_0=−1\) y\( y_0=2\). Dado que la pendiente de la solución en este punto es igual a\( −3\), podemos utilizar el método de aproximación lineal para aproximar y cerca\( (−1,2)\).
\[ L(x)=y_0+f′(x_0)(x−x_0).\nonumber \]
Aquí\( x_0=−1,y_0=2,\) y\( f′(x_0)=−3,\) así la aproximación lineal se convierte
\[ L(x)=2−3(x−(−1))=2−3x−3=−3x−1.\nonumber \]
Ahora elegimos un tamaño de paso. El tamaño del paso es un valor pequeño, típicamente\( 0.1\) o menor, que sirve como incremento para\( x\); está representado por la variable\( h\). En nuestro ejemplo, vamos\( h=0.1\). Incrementar\( x_0\) por\( h\) da nuestro siguiente\( x\) valor:
\[ x_1=x_0+h=−1+0.1=−0.9.\nonumber \]
Podemos sustituir\( x_1=−0.9\) en la aproximación lineal para calcular\( y_1\).
\[ y_1=L(x_1)=−3(−0.9)−1=1.7.\nonumber \]
Por lo tanto el\( y\) valor aproximado para la solución cuando\( x=−0.9\) es\( y=1.7\). Luego podemos repetir el proceso, utilizando\( x_1=−0.9\) y\( y_1=1.7\) para calcular\( x_2\) y\( y_2\). La nueva pendiente viene dada por\( y'=(−0.9)^2−(1.7)^2=−2.08.\) Primero,\( x_2=x_1+h=−0.9+0.1=−0.8.\) Usando aproximación lineal da
\ (\ begin {alinear*} L (x) &=y_1+f′ (x_1) (x−x_1)\\ [4pt]
&=1.7−2.08 (x− (−0.9))\\ [4pt]
&=1.7−2.08x−1.872\\ [4pt]
&=−2.08x−0.172. \ end {alinear*}\)
Finalmente, sustituimos\( x_2=−0.8\) en la aproximación lineal para calcular\( y_2\).
\ (\ begin {align*} Y_2&=L (x_2)\\ [4pt]
&=−2.08x_2−0.172\\ [4pt]
&=−2.08 (−0.8) −0.172\\ [4pt]
&=1.492. \ end {alinear*}\)
Por lo tanto, el valor aproximado de la solución a la ecuación diferencial es\( y=1.492\) cuando\( x=−0.8.\)
Lo que acabamos de mostrar es la idea detrás del Método de Euler. Repitiendo estos pasos da una lista de valores para la solución. Estos valores se muestran en la tabla, redondeados a cuatro decimales.
| \( n\) | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| \( x_n\) | −1 | −0.9 | −0.8 | −0.7 | −0.6 | −0.5 |
| \( y_n\) | 2 | 1.7 | 1.492 | 1.3334 | 1.2046 | 1.0955 |
| \( n\) | 6 | 7 | 8 | 9 | 10 | |
| \( x_n\) | −0.4 | −0.3 | −0.2 | −0.1 | 0 | |
| \( y_n\) | 1.0004 | 1.9164 | 1.8414 | 1.7746 | 1.7156 |
Considere el problema del valor inicial
\[ y'=f(x,y),\; y(x_0)=y_0.\nonumber \]
Para aproximar una solución a este problema usando el método de Euler, defina
\( x_n=x_0+nh\)
\( y_n=y_{n−1}+hf(x_{n−1},y_{n−1})\).
Aquí\( h>0\) representa el tamaño del paso y\( n\) es un número entero, empezando por\( 1\). El número de pasos realizados es contado por la variable\( n\).
Normalmente\( h\) es un valor pequeño, digamos\( 0.1\) o\( 0.05\). Cuanto menor sea el valor de\( h\), más cálculos se necesitan. Cuanto mayor sea el valor de\( h\), menos cálculos se necesitan. Sin embargo, el compromiso da como resultado un menor grado de precisión para un tamaño de paso más grande, como se ilustra en la Figura\( \PageIndex{9}\).
Considere el problema del valor inicial
\[ y′=3x^2−y^2+1,\; y(0)=2.\nonumber \]
Utilice el método de Euler con un tamaño de paso de\( 0.1\) para generar una tabla de valores para la solución para valores de\( x\) entre\( 0\) y\( 1\).
Solución
Nos dan\( h=0.1\) y\( f(x,y)=3x^2−y^2+1.\) además, la condición inicial\( y(0)=2\) da\( x_0=0\) y\( y_0=2\). Usando Ecuación con\( n=0\), podemos generar esta tabla.
| \( n\) | \( x_n\) | \( y_n=y_{n−1}+hf(x_{n−1},y_{n−1})\) |
|---|---|---|
| \ (n\)” style="vertical-align:middle; ">0 | \ (x_n\)” style="vertical-align:middle; ">0 | \ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="vertical-align:middle; ">2 |
| \ (n\)” style="vertical-align:middle; ">1 | \ (x_n\)” style="vertical-align:middle; ">0.1 | \ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="vertical-align:middle; ">\( y_1=y_0+hf(x_0,y_0)=1.7\) |
| \ (n\)” style="vertical-align:middle; ">2 | \ (x_n\)” style="vertical-align:middle; ">0.2 | \ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="vertical-align:middle; ">\( y_2=y_1+hf(x_1,y_1)=1.514\) |
| \ (n\)” style="vertical-align:middle; ">3 | \ (x_n\)” style="vertical-align:middle; ">0.3 | \ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="vertical-align:middle; ">\( y_3=y_2+hf(x_2,y_2)=1.3968\) |
| \ (n\)” style="vertical-align:middle; ">4 | \ (x_n\)” style="vertical-align:middle; ">0.4 | \ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="vertical-align:middle; ">\( y_4=y_3+hf(x_3,y_3)=1.3287\) |
| \ (n\)” style="vertical-align:middle; ">5 | \ (x_n\)” style="vertical-align:middle; ">0.5 | \ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="vertical-align:middle; ">\( y_5=y_4+hf(x_4,y_4)=1.3001\) |
| \ (n\)” style="vertical-align:middle; ">6 | \ (x_n\)” style="vertical-align:middle; ">0.6 | \ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="vertical-align:middle; ">\( y_6=y_5+hf(x_5,y_5)=1.3061\) |
| \ (n\)” style="vertical-align:middle; ">7 | \ (x_n\)” style="vertical-align:middle; ">0.7 | \ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="vertical-align:middle; ">\( y_7=y_6+hf(x_6,y_6)=1.3435\) |
| \ (n\)” style="vertical-align:middle; ">8 | \ (x_n\)” style="vertical-align:middle; ">0.8 | \ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="vertical-align:middle; ">\( y_8=y_7+hf(x_7,y_7)=1.4100\) |
| \ (n\)” style="vertical-align:middle; ">9 | \ (x_n\)” style="vertical-align:middle; ">0.9 | \ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="vertical-align:middle; ">\( y_9=y_8+hf(x_8,y_8)=1.5032\) |
| \ (n\)” style="vertical-align:middle; ">10 | \ (x_n\)” style="vertical-align:middle; ">1.0 | \ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="vertical-align:middle; ">\( y_{10}=y_9+hf(x_9,y_9)=1.6202\) |
Con diez cálculos, somos capaces de aproximar los valores de la solución al problema del valor inicial para valores de\( x\) entre\( 0\) y\( 1\).
Vaya a este sitio web para tener la oportunidad de explorar visualmente el método de Euler.
Considere el problema del valor inicial
\[ y′=x^3+y^2,\; y(1)=−2.\nonumber \]
Usando un tamaño de paso de\( 0.1\), generar una tabla con valores aproximados para la solución al problema del valor inicial para valores de\( x\) entre\( 1\) y\( 2\).
- Pista
-
Comience por identificar el valor de\( h\), luego averiguar qué\( f(x,y)\) es. Luego usa la fórmula del Método de Euler para calcular\( y_1,y_2,\) y así sucesivamente.
- Responder
-
Tabla\( \PageIndex{3}\): Usando el Método de Euler para aproximar soluciones a la ecuación diferencial en Ejercicio\(\PageIndex{3}\). \( n\) \ (x_n) \( y_n=y_{n−1}+hf(x_{n−1},y_{n−1})\) 0 1 −2 1 1.1 \( y_1=y_0+hf(x_0,y_0)=−1.5\) 2 1.2 \( y_2=y_1+hf(x_1,y_1)=−1.1419\) 3 1.3 \( y_3=y_2+hf(x_2,y_2)=−0.8387\) 4 1.4 \( y_4=y_3+hf(x_3,y_3)=−0.5487\) 5 1.5 \( y_5=y_4+hf(x_4,y_4)=−0.2442\) 6 1.6 \( y_6=y_5+hf(x_5,y_5)=0.0993\) 7 1.7 \( y_7=y_6+hf(x_6,y_6)=0.5099\) 8 1.8 \( y_8=y_7+hf(x_7,y_7)=1.0272\) 9 1.9 \( y_9=y_8+hf(x_8,y_8)=1.7159\) 10 2 \( y_{10}=y_9+hf(x_9,y_9)=2.6962\)
Conceptos clave
- Un campo de dirección es un objeto matemático utilizado para representar gráficamente soluciones a una ecuación diferencial de primer orden.
- El Método de Euler es una técnica numérica que se puede utilizar para aproximar soluciones a una ecuación diferencial.
Ecuaciones Clave
- Método de Euler
\( x_n=x_0+nh\)
\( y_n=y_{n−1}+hf(x_{n−1},y_{n−1})\), donde\( h\) esta el tamaño del paso
Glosario
- solución asintóticamente semi-estable
- \( y=k\)si no es asintóticamente estable ni asintóticamente inestable
- solución asintóticamente estable
- \( y=k\)si existe\( ε>0\) tal que por cualquier valor\( c∈(k−ε,\, k+ε)\) la solución al problema del valor inicial se\( y′=f(x,y),\; y(x_0)=c\) aproxima\( k\) como se\( x\) acerca al infinito
- solución asintóticamente inestable
- \( y=k\)si existe\( ε>0\) tal que por cualquier valor\( c∈(k−ε,\, k+ε)\) la solución al problema del valor inicial\( y′=f(x,y),\; y(x_0)=c\) nunca se acerca\( k\) como se\( x\) acerca al infinito
- campo de dirección (campo de pendiente)
- un objeto matemático utilizado para representar gráficamente soluciones a una ecuación diferencial de primer orden; en cada punto de un campo de dirección, aparece un segmento de línea cuya pendiente es igual a la pendiente de una solución a la ecuación diferencial que pasa por ese punto
- solución de equilibrio
- cualquier solución a la ecuación diferencial de la forma\( y=c,\) donde\( c\) es una constante
- Método de Euler
- una técnica numérica utilizada para aproximar soluciones a un problema de valor inicial
- curva de solución
- una curva graficada en un campo de dirección que corresponde a la solución al problema del valor inicial que pasa por un punto dado en el campo de dirección
- tamaño de paso
- el incremento hh que se suma al valor xx en cada paso del Método de Euler
Colaboradores y Atribuciones
- Template:ContribOpenStaxCalc
- Paul Seeburger (Monroe Community College) edited this section to adjust the explanation of equilibrium points in the example shown in Figures \( \PageIndex{4}\) - \( \PageIndex{6}\). He also created these figures.