8.3E: Ejercicios para la Sección 8.3

En los ejercicios 1 - 4, resuelve los siguientes problemas de valor inicial con la condición inicial\( y_0=0\) y grafica la solución.

1)\( \dfrac{dy}{dt}=y+1\)

Contestar

\( y=e^t−1\)

2)\( \dfrac{dy}{dt}=y−1\)

3)\( \dfrac{dy}{dt}=-y+1\)

Contestar

\( y=1−e^{−t}\)

4)\( \dfrac{dy}{dt}=−y−1\)

En los ejercicios 5 - 14, encuentra la solución general a la ecuación diferencial.

5)\( x^2y'=(x+1)y\)

Contestar

\( y=Cxe^{−1/x}\)

6)\( y'=\tan(y)x\)

7)\( y'=2xy^2\)

Contestar

\( y=\dfrac{1}{C−x^2}\)

8)\( \dfrac{dy}{dt}=y\cos(3t+2)\)

9)\( 2x\dfrac{dy}{dx}=y^2\)

Contestar

\( y=−\dfrac{2}{C+\ln|x|}\)

10)\( y'=e^yx^2\)

11)\( (1+x)y'=(x+2)(y−1)\)

Contestar

\( y=Ce^x(x+1)+1\)

12)\( \dfrac{dx}{dt}=3t^2(x^2+4)\)

13)\( t\dfrac{dy}{dt}=\sqrt{1−y^2}\)

Contestar

\( y=\sin(\ln|t|+C)\)

14)\( y'=e^xe^y\)

En los ejercicios 15 - 24, encuentra la solución al problema del valor inicial.

15)\( y'=e^{y−x}, \quad y(0)=0\)

Contestar

\( y=−\ln(e^{−x})\)lo que simplifica\(y = x\)

16)\( y'=y^2(x+1), \quad y(0)=2\)

17)\( \dfrac{dy}{dx}=y^3xe^{x^2}, \quad y(0)=1\)

Contestar

\( y=\dfrac{1}{\sqrt{2−e^{x^2}}}\)

18)\( \dfrac{dy}{dt}=y^2e^x\sin(3x), \quad y(0)=1\)

19)\( y'=\dfrac{x}{\text{sech}^2y}, \quad y(0)=0\)

Contestar

\( y=\tanh^{−1}\left(\dfrac{x^2}{2}\right)\)

20)\( y'=2xy(1+2y), \quad y(0)=−1\)

21)\( \dfrac{dx}{dt}=\ln(t)\sqrt{1−x^2}, \quad x(1)=0\)

Contestar

\( x=\sin(1 - t + t\ln t)\)

22)\( y'=3x^2(y^2+4),\quad y(0)=0\)

23)\( y'=e^y5^x, \quad y(0)=\ln(\ln(5))\)

Contestar

\( y=\ln(\ln(5))−\ln(2−5^x)\)

24)\( y'=−2x\tan(y), \quad y(0)=\dfrac{π}{2}\)

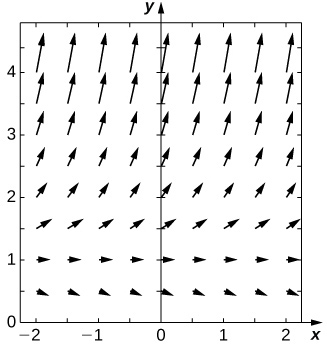
Para problemas 25 - 29, utilice un programa de software o su calculadora para generar los campos direccionales. Resuelva explícitamente y dibuje curvas de solución para varias condiciones iniciales. ¿Existen algunas condiciones iniciales críticas que cambien el comportamiento de la solución?

25) [T]\( y'=1−2y\)

Contestar

\( y=Ce^{−2}x+\dfrac{1}{2}\)

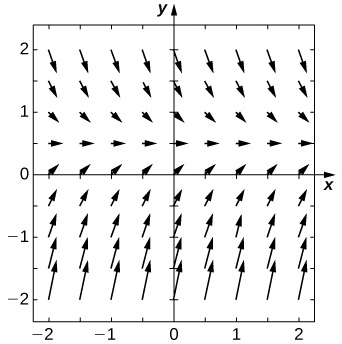
26) [T]\( y'=y^2x^3\)

27) [T]\( y'=y^3e^x\)

Contestar

\( y=\dfrac{1}{\sqrt{2}\sqrt{C−e^x}}\)

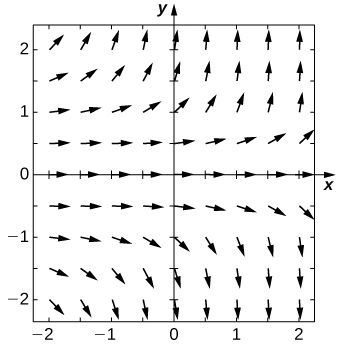
28) [T]\( y'=e^y\)

29) [T]\( y'=y\ln(x)\)

Contestar

\( y=Ce^{−x}x^x\)

30) La mayoría de los fármacos en el torrente sanguíneo se descomponen según la ecuación\( y'=cy\), donde\( y\) está la concentración del fármaco en el torrente sanguíneo. Si la vida media de un medicamento es de\( 2\) horas, ¿qué fracción de la dosis inicial queda después de\( 6\) horas?

31) Un fármaco se administra por vía intravenosa a un paciente a una tasa\( r\) mg/h y se limpia del cuerpo a una velocidad proporcional a la cantidad de fármaco aún presente en el cuerpo,\( d\) Configurar y resolver la ecuación diferencial, suponiendo que no haya fármaco inicialmente presente en el cuerpo.

Contestar

\( y=\frac{r}{d}(1−e^{−dt})\)

32) [T] ¿Con qué frecuencia se debe tomar un medicamento si su dosis es de\( 3\) mg, se aclara a una tasa\( c=0.1\) mg/h, y se requiere que\( 1\) mg esté en el torrente sanguíneo en todo momento?

33) Un tanque contiene\( 1\) kilogramo de sal disuelta en\( 100\) litros de agua. Una solución salina de\( 0.1\) kg sal/L se bombea al tanque a una velocidad de\( 2\) L/min y se drena a la misma velocidad. Resolver la concentración de sal en el momento\( t\). Supongamos que el tanque está bien mezclado.

Contestar

\( y(t)=10−9e^{−t/50}\)

34) Un tanque que contiene\( 10\) kilogramos de sal disueltos en\( 1000\) litros de agua tiene dos soluciones salinas bombeadas. La primera solución de\( 0.2\) kg sal/l se bombea a una velocidad de\( 20\) L/min y la segunda solución de\( 0.05\) kg sal/l se bombea a una velocidad de\( 5\) L/min. El tanque drena a\( 25\) L/min. Supongamos que el tanque está bien mezclado. Resolver la concentración de sal en el momento\( t\).

35) [T] Para el problema anterior, encuentra cuánta sal hay en el tanque\( 1\) hora después de que comience el proceso.

Contestar

\( 134.3\)kilogramos

36) La ley de Torricelli establece que para un tanque de agua con un agujero en el fondo que tiene una sección transversal de\( A\) y con una altura de agua\( h\) por encima del fondo del tanque, la tasa de cambio de volumen de agua que fluye desde el tanque es proporcional a la raíz cuadrada de la altura del agua, según a\( \dfrac{dV}{dt}=−A\sqrt{2gh}\), donde\( g\) esta la aceleracion debida a la gravedad. Tenga en cuenta que\( \dfrac{dV}{dt}=A\dfrac{dh}{dt}\). Resolver el problema de valor inicial resultante para la altura del agua, asumiendo un tanque con un agujero de radio\( 2\) ft. La altura inicial del agua es\( 100\) ft.

37) Para el problema anterior, determine cuánto tiempo tarda el tanque en drenar.

Contestar

\( 720\)segundos

Para problemas 38 - 44, use la ley de enfriamiento de Newton.

38) La base líquida de un helado tiene una temperatura inicial de\( 200°F\) antes de colocarlo en un congelador con una temperatura constante de\( 0°F\). Después de\( 1\) hora, la temperatura de la base de helado ha disminuido a\( 140°F\). Formular y resolver el problema del valor inicial para determinar la temperatura del helado.

39) [T] La base líquida de un helado tiene una temperatura inicial de\( 210°F\) antes de colocarlo en un congelador con una temperatura constante de\( 20°F\). Después de\( 2\) horas, la temperatura de la base de helado ha disminuido a\( 170°F\). ¿A qué hora estará listo para comer el helado? (Supongamos que\( 30°F\) es la temperatura óptima para comer.)

Contestar

\( 24\)horas\( 55\) minutos

40) [T] Estás organizando un helado social. La temperatura exterior es\( 80°F\) y el helado está en\( 10°F\). Después de\( 10\) minutos, la temperatura del helado ha subido por\( 10°F\). ¿Cuánto tiempo más puedes esperar antes de que se derrita el helado\( 40°F\)?

41) Tienes una taza de café a temperatura\( 70°C\) y la temperatura ambiente en la habitación es\( 20°C\). Suponiendo una velocidad\( k\) de enfriamiento de\( 0.125,\) escritura y resolver la ecuación diferencial para describir la temperatura del café con respecto al tiempo.

Contestar

\( T(t)=20+50e^{−0.125t}\)

42) [T] Tienes una taza de café a temperatura\( 70°C\) que pones afuera, donde está la temperatura ambiente\( 0°C.\) Después de\( 5\) minutos, ¿cuánto más frío es el café?

43) Tienes una taza de café a temperatura\( 70°C\) e inmediatamente viertes en\( 1\) parte leche a\( 5\) partes de café. La leche está inicialmente a temperatura\( 1°C.\) Escribe y resuelve la ecuación diferencial que gobierna la temperatura de este café.

Contestar

\( T(t)=20+38.5e^{−0.125t}\)

44) Tienes una taza de café a temperatura\( 70°C,\) que dejas enfriar\( 10\) minutos antes de verter la misma cantidad de leche a la\( 1°C\) que en el problema anterior. ¿Cómo se compara la temperatura con la copa anterior después de\( 10\) minutos?

45) Resolver el problema genérico\( y'=ay+b\) con condición inicial\( y(0)=c.\)

Contestar

\( y=(c+ba)e^{ax}−\frac{b}{a}\)

46) Demostrar la ecuación básica de interés compuesto continuo. Asumiendo un depósito inicial\( P_0\) y una tasa de interés de\( r\), establecer y resolver una ecuación para intereses continuamente compuestos.

47) Asumir una cantidad inicial nutritiva de\( I\) kilogramos en un tanque con\( L\) litros. Supongamos que se bombea una concentración de\( c\) Kg/L a una velocidad de\( r\) L/min. El tanque está bien mezclado y se drena a una velocidad de\( r\) L/min. Encuentra la ecuación que describe la cantidad de nutriente en el tanque.

Contestar

\( y(t)=cL+(I−cL)e^{−rt/L}\)

48) Las hojas se acumulan en el suelo del bosque a razón de\( 2\) g/cm ² /año y también se descomponen a una\( 90%\) tasa anual. Escribir una ecuación diferencial que rija el número de gramos de hojarasca por centímetro cuadrado de suelo forestal, suponiendo que en el momento no\( 0\) haya hojarasca en el suelo. ¿Esta cantidad se aproxima a un valor constante? ¿Cuál es ese valor?

49) Las hojas se acumulan en el suelo del bosque a razón de\( 4\) g/cm ² /año. Estas hojas se descomponen a razón de\( 10%\) por año. Escribir una ecuación diferencial que rija el número de gramos de hojarasca por centímetro cuadrado de suelo forestal. ¿Esta cantidad se aproxima a un valor constante? ¿Cuál es ese valor?

Contestar

Ecuación Diferencial:\(\dfrac{dy}{dt} = 4 - 0.1y\)
Solución, el modelo para esta situación:\( y=40(1−e^{−0.1t})\),
La cantidad se aproxima a un valor constante de 40 g/cm ²