8.4E: Ejercicios para la Sección 8.4

Última actualización
Guardar como PDF

Page ID: 116243

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Modelo Logístico Básico

Para los problemas 1 - 11, considere la ecuación logística en la forma\( P'=CP−P^2.\) Dibujar el campo direccional y encontrar la estabilidad de los equilibrios.

1)\( C=3\)

2)\( C=0\)

Contestar

\( P=0\)semi-estable

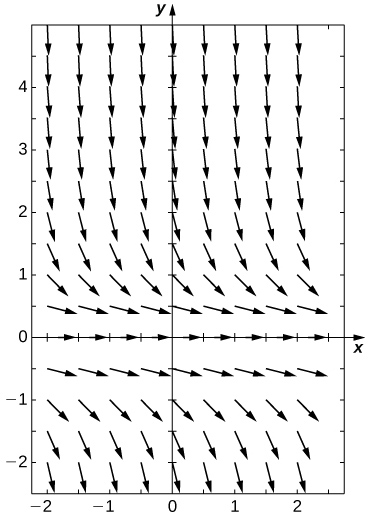
3)\( C=−3\)

4) Resolver la ecuación logística para\( C=10\) y una condición inicial de\( P(0)=2.\)

Contestar: \( P=\dfrac{10e^{10x}}{e^{10x}+4}\)

5) Resolver la ecuación logística para\( C=−10\) y una condición inicial de\( P(0)=2\).

6) Una población de ciervos dentro de un parque tiene una capacidad de carga\( 200\) y una tasa de crecimiento de\( 2%\). Si la población inicial es\( 50\) venado, ¿cuál es la población de venados en un momento dado?

Contestar: \( P(t)=\dfrac{10000e^{0.02t}}{150+50e^{0.02t}}\)

7) Una población de ranas en un estanque tiene una tasa de crecimiento de\( 5%.\) Si la población inicial son\( 1000\) ranas y la capacidad de carga lo es\( 6000\), ¿cuál es la población de ranas en un momento dado?

8) [T] Las bacterias crecen a una velocidad\( 20%\) por hora en una placa de Petri. Si inicialmente hay una bacteria y una capacidad de carga de\( 1\) millones de células, ¿cuánto tiempo se tarda en llegar a\( 500,000\) las células?

Contestar: \( 69\)horas\( 5\) minutos

9) [T] Los conejos en un parque tienen una población inicial de\( 10\) y crecen a una\( 4%\) tasa anual. Si la capacidad de carga es\( 500\), ¿a qué hora llega la población a\( 100\) los conejos?

10) [T] Dos monos son colocados en una isla. Después de\( 5\) años, hay\( 8\) monos, y la capacidad de carga estimada son\( 25\) los monos. ¿Cuándo llega la población de monos a\( 16\) los monos?

Contestar: \( 8\)años\( 11\) meses

11) [T] Se construye un santuario de mariposas que puede contener\( 2000\) mariposas, y\( 400\) las mariposas se trasladan inicialmente. Si después de\( 2\) meses ahora hay\( 800\) mariposas, ¿cuándo llega la población a\( 1500\) las mariposas?

Modelo Logístico de Población con Agotamiento

Los siguientes problemas consideran la ecuación logística con un término agregado para el agotamiento, ya sea por muerte o emigración.

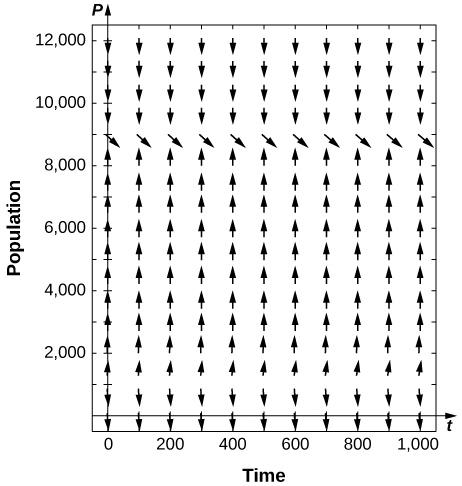
12) [T] La población de truchas en un estanque viene dada por\( P'=0.4P\left(1−\dfrac{P}{10000}\right)−400\), donde se capturan\( 400\) truchas por año. Use su calculadora o software de computadora para dibujar un campo direccional y dibujar algunas soluciones de muestra. ¿Qué esperas del comportamiento?

Contestar

13) En el problema anterior, ¿cuáles son las estabilidades de los equilibrios\( 0<P_1<P_2\)?

14) [T] Para el problema anterior, utilice software para generar un campo direccional para el valor\( f=400\). ¿Cuáles son las estabilidades de los equilibrios?

Contestar

\( P_1\)semi-estable

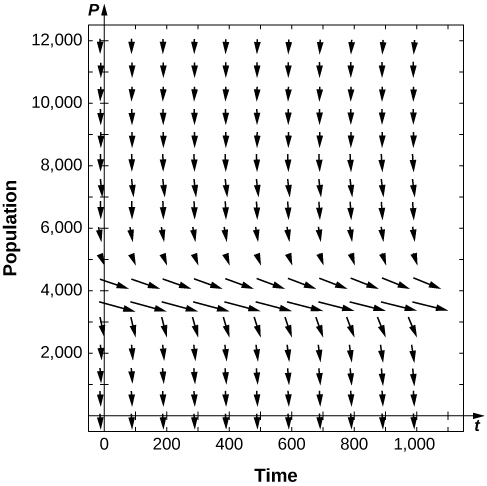
15) [T] Para los problemas anteriores, utilizar software para generar un campo direccional para el valor\( f=600.\) ¿Cuáles son las estabilidades de los equilibrios?

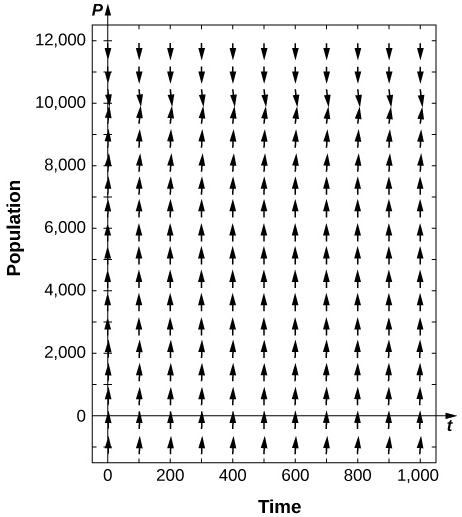
16) [T] Para los problemas anteriores, considere el caso donde se agrega un cierto número de peces al estanque, o\( f=−200.\) ¿Cuáles son los equilibrios no negativos y sus estabilidades?

Contestar

\( P_2>0\)estable

Es más probable que la cantidad de pesca se rija por el número actual de peces presentes, por lo que en lugar de capturar un número constante de peces, la tasa es proporcional al número actual de peces presentes, con proporcionalidad constante\( k\), ya que\( P'=0.4P\left(1−\dfrac{P}{10000}\right)−kP.\)

17) [T] Para el problema de pesca anterior, dibujar un campo direccional asumiendo\( k=0.1\). Dibuje algunas soluciones que exhiban este comportamiento. ¿Cuáles son los equilibrios y cuáles son sus estabilidades?

18) [T] Utilice software o una calculadora para dibujar campos direccionales para\( k=0.4\). ¿Cuáles son los equilibrios no negativos y sus estabilidades?

Contestar

\( P_1=0\)es semi-estable

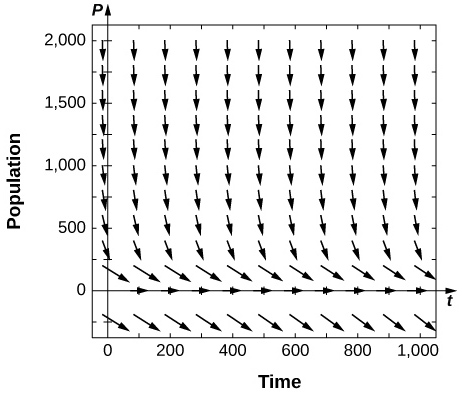
19) [T] Utilice software o una calculadora para dibujar campos direccionales para\( k=0.6\). ¿Cuáles son los equilibrios y sus estabilidades?

20) Resolver esta ecuación, asumiendo un valor de\( k=0.05\) y una condición inicial del\( 2000\) pez.

Contestar: \( y=\dfrac{−20}{4×10^{−6}−0.002e^{0.01t}}\)

21) Resolver esta ecuación, asumiendo un valor de\( k=0.05\) y una condición inicial del\( 5000\) pez.

Umbrales Mínimos de Población Sostenible

Los siguientes problemas agregan un valor umbral mínimo para que la especie sobreviva,\( T\), lo que cambia la ecuación diferencial a\( P'(t)=rP\left(1−\dfrac{P}{K}\right)\left(1−\dfrac{T}{P}\right)\).

22) Dibujar el campo direccional de la ecuación logística umbral, asumiendo\( K=10,r=0.1,T=2\). ¿Cuándo sobrevive la población? ¿Cuándo se extingue?

Contestar

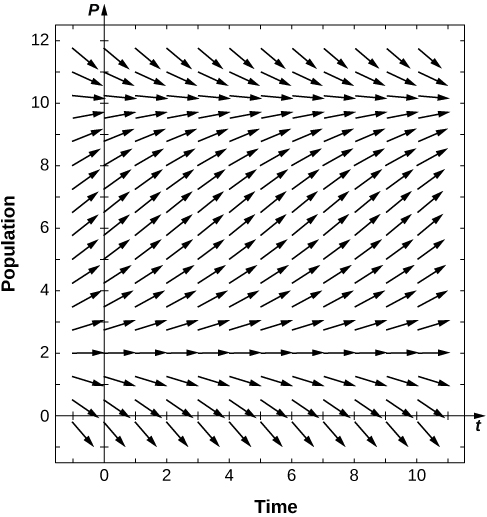
23) Para el problema anterior, resolver la ecuación del umbral logístico, asumiendo la condición inicial\( P(0)=P_0\).

24) Los tigres de Bengala en un parque de conservación tienen una capacidad de carga\( 100\) y necesitan un mínimo de\( 10\) para sobrevivir. Si crecen en población a una\( 1%\) tasa anual, con una población inicial de\( 15\) tigres, resuelven por el número de tigres presentes.

Contestar: \( P(t)=\dfrac{850+500e^{0.009t}}{85+5e^{0.009t}}\)

25) Un bosque que contiene lémures de cola anular en Madagascar tiene el potencial de apoyar a\( 5000\) los individuos, y la población de lémures crece a una\( 5%\) tasa anual. Se necesita un mínimo de 500 individuos para que los lémures sobrevivan. Dada una población inicial de\( 600\) lémures, resolver para la población de lémures.

26) La población de leones de montaña en el norte de Arizona tiene una capacidad de carga estimada\( 250\) y crece a una\( 0.25%\) tasa anual y debe haber\( 25\) para que la población sobreviva. Con una población inicial de leones de\( 30\) montaña, ¿cuántos años se tardará en sacar a los leones de la lista de especies en peligro de extinción (al menos\( 100\))?

Contestar: \( 13\)años meses

La ecuación de Gompertz

Las siguientes preguntas consideran la ecuación de Gompertz, una modificación para el crecimiento logístico, que a menudo se utiliza para modelar el crecimiento del cáncer, específicamente el número de células tumorales.

27) La ecuación de Gompertz viene dada por\( P(t)'=α\ln\left(\frac{K}{P(t)}\right)P(t).\) Dibujar los campos direccionales para esta ecuación asumiendo que todos los parámetros son positivos, y dado que\( K=1.\)

28) Supongamos que para una población,\( K=1000\) y\( α=0.05\). Dibuje el campo direccional asociado a esta ecuación diferencial y dibuje algunas soluciones. ¿Cuál es el comportamiento de la población?

Contestar

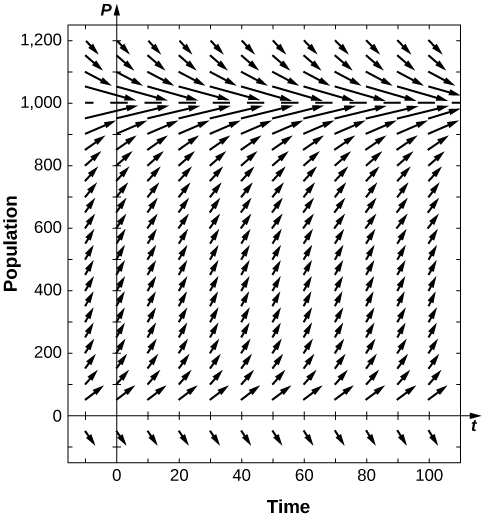
29) Resolver la ecuación de Gompertz para genéricos\( α\) y\( K\) y\( P(0)=P_0\).

30) [T] La ecuación de Gompertz se ha utilizado para modelar el crecimiento tumoral en el cuerpo humano. Partiendo de una célula tumoral en el día\( 1\) y asumiendo\( α=0.1\) y una capacidad de carga de\( 10\) millones de células, ¿cuánto tiempo se tarda en llegar a la etapa de “detección” a\( 5\) millones de células?

Contestar: \( 31.465\)días

31) [T] Se estima que la población humana mundial llegó a\( 3\) mil millones de personas en\( 1959\) y\( 6\) mil millones en\( 1999\). Asumiendo una capacidad de carga de\( 16\) mil millones de humanos, escribir y resolver la ecuación diferencial para el crecimiento logístico, y determinar en qué año la población alcanzó los\( 7\) mil millones.

32) [T] Se estima que la población humana mundial llegó a\( 3\) mil millones de personas en\( 1959\) y\( 6\) mil millones en\( 1999\). Asumiendo una capacidad de carga de\( 16\) mil millones de humanos, escribir y resolver la ecuación diferencial para el crecimiento de Gompertz, y determinar en qué año la población alcanzó los\( 7\) mil millones. Fue el crecimiento logístico o el crecimiento de Gompertz más exacto, considerando que la población mundial alcanzó\( 7\) mil millones en octubre\( 31,2011?\)

Contestar: septiembre\( 2008\)

33) Demostrar que la población crece más rápido cuando alcanza la mitad de la capacidad de carga para la ecuación logística\( P'=rP\left(1−\dfrac{P}{K}\right)\).

34) ¿Cuándo aumenta la población más rápido en la ecuación logística de umbral\( P'(t)=rP\left(1−\dfrac{P}{K}\right)\left(1−\dfrac{T}{P}\right)\)?

Contestar: \( \dfrac{K+T}{2}\)

35) ¿Cuándo aumenta la población más rápido para la ecuación de Gompertz?\( P(t)'=α\ln\left(\frac{K}{P(t)}\right)P(t)?\)

A continuación se muestra una tabla de las poblaciones de grullas ferinas en estado salvaje desde\( 1940\) hasta\( 2000\). La población se recuperó de cerca de la extinción luego de que comenzaron los esfuerzos de conservación Los siguientes problemas consideran la aplicación de modelos de población para adecuar los datos. Asumir una capacidad de carga de\( 10,000\) grúas. Ajustar los datos asumiendo años desde entonces\( 1940\) (por lo que su población inicial en el momento\( 0\) serían\( 22\) grúas).

Año (años desde que comenzó la conservación)	Población Grulla Ferina
1940 (0)	22
1950 (10)	31
1960 (20)	36
1970 (30)	57
1980 (40)	91
1990 (50)	159
2000 (60)	256

Origen: https://www.savingcranes.org/images/...wc_numbers.pdf

36) Encontrar la ecuación y el parámetro\( r\) que mejor se ajusten a los datos para la ecuación logística.

Contestar: \( r=0.0405\)

37) Encontrar la ecuación y los parámetros\( r\) y\( T\) que mejor se ajusten a los datos para la ecuación logística de umbral.

38) Encontrar la ecuación y el parámetro\( α\) que mejor se ajusten a los datos para la ecuación de Gompertz.

Contestar: \( α=0.0081\)

39) Grafique las tres soluciones y los datos en la misma gráfica. ¿Qué modelo parece ser el más preciso?

40) Utilizando las tres ecuaciones encontradas en los problemas anteriores, estimar la población en\( 2010\) (año\( 70\) después de la conservación). La población real medida en ese momento fue\( 437\). ¿Qué modelo es el más preciso?

Contestar: Logístico:\( 361\), Umbral:\( 436\), Gompertz:\( 309\).