8.5: Ecuaciones lineales de primer orden

Objetivos de aprendizaje

• Escribir una ecuación diferencial lineal de primer orden en forma estándar.
• Encuentre un factor integrador y utilícelo para resolver una ecuación diferencial lineal de primer orden.
• Resolver problemas aplicados que involucran ecuaciones diferenciales lineales de primer orden.

Anteriormente, estudiamos una aplicación de una ecuación diferencial de primer orden que implicaba resolver la velocidad de un objeto. En particular, si una pelota es lanzada hacia arriba con una velocidad inicial de\( v_0\) pies/s, entonces un problema de valor inicial que describe la velocidad de la pelota después de\( t\) segundos viene dado por

\[ \dfrac{dv}{dt}=−32 \nonumber \]

con\(v(0)=v_0.\)

Este modelo asume que la única fuerza que actúa sobre la pelota es la gravedad. Ahora nos sumamos al problema al permitir la posibilidad de que la resistencia del aire actúe sobre la pelota.

La resistencia al aire siempre actúa en la dirección opuesta al movimiento. Por lo tanto, si un objeto está subiendo, la resistencia al aire actúa en dirección descendente. Si el objeto está cayendo, la resistencia al aire actúa en dirección ascendente (Figura\( \PageIndex{1}\)). No existe una relación exacta entre la velocidad de un objeto y la resistencia al aire que actúa sobre él. Para objetos muy pequeños, la resistencia del aire es proporcional a la velocidad; es decir, la fuerza debida a la resistencia del aire es numéricamente igual a algunos\( k\) tiempos constantes\( v\). Para objetos más grandes (por ejemplo, del tamaño de béisbol), dependiendo de la forma, la resistencia al aire puede ser aproximadamente proporcional al cuadrado de la velocidad. De hecho, la resistencia al aire puede ser proporcional a\( v^{1.5}\), o\( v^{0.9}\), o alguna otra potencia de\( v\).

Figura\( \PageIndex{1}\): Fuerzas que actúan sobre una pelota de béisbol en movimiento: la gravedad actúa en dirección descendente y la resistencia al aire actúa en una dirección opuesta a la dirección del movimiento.

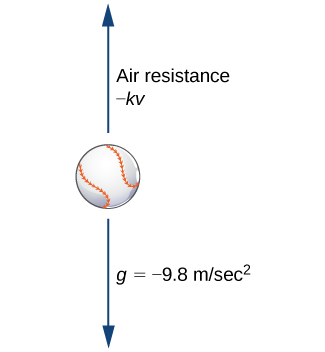
Trabajaremos con la aproximación lineal para la resistencia al aire. Si asumimos\( k>0\), entonces la expresión para la fuerza\( F_A\) debido a la resistencia aérea viene dada por\( FA_=−kv\). Por lo tanto, la suma de las fuerzas que actúan sobre el objeto es igual a la suma de la fuerza gravitacional y la fuerza debida a la resistencia del aire. Esto, a su vez, es igual a la masa del objeto multiplicada por su aceleración en el tiempo\( t\) (segunda ley de Newton). Esto nos da la ecuación diferencial

\[ m\dfrac{dv}{dt}=−kv−mg. \nonumber \]

Finalmente, imponemos una condición inicial\( v(0)=v_0,\) donde\( v_0\) es la velocidad inicial medida en metros por segundo. Esto hace que\( g=9.8m/s^2.\) el problema del valor inicial se convierta

\[ m\dfrac{dv}{dt}=−kv−mg \nonumber \]

con\(v(0)=v_0.\)

La ecuación diferencial en este problema de valor inicial es un ejemplo de una ecuación diferencial lineal de primer orden. (Recordemos que una ecuación diferencial es de primer orden si la derivada de orden superior que aparece en la ecuación es\( 1\).) En esta sección, estudiamos ecuaciones lineales de primer orden y examinamos un método para encontrar una solución general a este tipo de ecuaciones, así como resolver problemas de valor inicial que las involucran.

Definición: Ecuación diferencial lineal de primer orden

Una ecuación diferencial de primer orden es lineal si se puede escribir en la forma

\[a(x)y′+b(x)y=c(x), \nonumber \]

donde\( a(x),b(x),\) y\( c(x)\) son funciones arbitrarias de\( x\).

Recuerde que la función desconocida\( y\) depende de la variable\( x\); es decir,\( x\) es la variable independiente y\( y\) es la variable dependiente. Algunos ejemplos de ecuaciones diferenciales lineales de primer orden son

\[ (3x^2−4)y'+(x−3)y=\sin x \nonumber \]

\[ (\sin x)y'−(\cos x)y=\cot x \nonumber \]

\[ 4xy'+(3\ln x)y=x^3−4x. \nonumber \]

Ejemplos de ecuaciones diferenciales no lineales de primer orden incluyen

\[ (y')^4−(y')^3=(3x−2)(y+4) \nonumber \]

\[ 4y'+3y^3=4x−5 \nonumber \]

\[(y')^2=\sin y+\cos x. \nonumber \]

Estas ecuaciones son no lineales por términos como\( (y′)^4,y^3,\) etc. Debido a estos términos, es imposible poner estas ecuaciones en la misma forma que Ecuación.

Forma estándar

Considerar la ecuación diferencial

\[ (3x^2−4)y′+(x−3)y=\sin x. \nonumber \]

Nuestro principal objetivo en esta sección es derivar un método de solución para ecuaciones de esta forma. Es útil tener el coeficiente de\( y′\) ser igual a\( 1\). Para que esto suceda, dividimos ambos lados por\( 3x^2−4.\)

\[ y′+ \left(\dfrac{x−3}{3x^2−4} \right)y=\dfrac{\sin x}{3x^2−4} \nonumber \]

A esto se le llama la forma estándar de la ecuación diferencial. Lo usaremos más adelante al encontrar la solución a una ecuación diferencial lineal general de primer orden. Volviendo a la ecuación, podemos dividir ambos lados de la ecuación por\( a(x)\). Esto lleva a la ecuación

\[ y′+\dfrac{b(x)}{a(x)}y=\dfrac{c(x)}{a(x)}. \label{eq5} \]

Ahora define

\[ p(x)=\dfrac{b(x)}{a(x)} \nonumber \]

y

\[ q(x)=\dfrac{c(x)}{a(x)} \nonumber \]

Entonces la Ecuación\ ref {eq5} se convierte

\[ y′+p(x)y=q(x). \nonumber \]

Podemos escribir cualquier ecuación diferencial lineal de primer orden en esta forma, y esto se conoce como la forma estándar para una ecuación diferencial lineal de primer orden.

Ejemplo\( \PageIndex{1}\): Writing First-Order Linear Equations in Standard Form

Ponga cada una de las siguientes ecuaciones diferenciales lineales de primer orden en forma estándar. Identificar\( p(x)\) y\( q(x)\) para cada ecuación.

1. \( y'=3x−4y\)
2. \( \dfrac{3xy'}{4y−3}=2\)(aquí\( x>0\))
3. \( y=3y'−4x^2+5\)

Solución

a.\( 4y\) Añádese a ambos lados:

\( y'+4y=3x.\)

En esta ecuación,\( p(x)=4\) y\ | (q (x) =3x.\)

b. Multiplicar ambos lados por\( 4y−3\), luego restar\( 8y\) de cada lado:

\( \dfrac{3xy'}{4y−3}=2\)

\( 3xy'=2(4y−3)\)

\( 3xy'=8y−6\)

\( 3xy'−8y=−6.\)

Por último, dividir ambos lados por\( 3x\) para hacer el coeficiente de\( y'\) igual a\( 1\):

\( y'−\dfrac{8}{3x}y=−\dfrac{2}{3x}.\)

Esto es permisible porque en el enunciado original de este problema asumimos que\( x>0\). (Si\( x=0\) entonces la ecuación original se convierte\( 0=2\), que es claramente una declaración falsa.)

En esta ecuación,\( p(x)=−\dfrac{8}{3x}\) y\( q(x)=−\dfrac{2}{3x}\).

c. Restar\( y\) de cada lado y sumar\( 4x^2−5\):

\( 3y'−y=4x^2−5.\)

Siguiente divide ambos lados por\( 3\):

\( y'−\dfrac{1}{3}y=\dfrac{4}{3}x^2−\dfrac{5}{3}\).

En esta ecuación,\( p(x)=−\dfrac{1}{3}\) y\( q(x)=\dfrac{4}{3}x^2−\dfrac{5}{3}\).

Ejercicio\(\PageIndex{1}\)

Poner la ecuación\( \dfrac{(x+3)y'}{2x−3y−4}=5\) en forma estándar e identificar\( p(x)\) y\( q(x)\).

Pista

Multiplica ambos lados por el denominador común, luego recoge todos los términos que involucran\( y\) en un lado.

Contestar

\[ y'+\dfrac{15}{x+3}y=\dfrac{10x−20}{x+3} \nonumber \]

\[p(x)=\dfrac{15}{x+3} \nonumber \]

y

\[ q(x)=\dfrac{10x−20}{x+3} \nonumber \]

Factores integradores

Ahora desarrollamos una técnica de solución para cualquier ecuación diferencial lineal de primer orden. Comenzamos con la forma estándar de una ecuación diferencial lineal de primer orden:

\[ y'+p(x)y=q(x). \label{Deq1} \]

El primer término en el lado izquierdo de Ecuación es la derivada de la función desconocida, y el segundo término es el producto de una función conocida con la función desconocida. Esto recuerda algo a la regla del poder. Si multiplicamos la ecuación\ ref {Deq1} por una función aún por determinar\( μ(x)\), entonces la ecuación se convierte

\[ μ(x)y′+μ(x)p(x)y=μ(x)q(x). \label{Deq2} \]

La Ecuación del lado izquierdo\ ref {Deq2} puede coincidir perfectamente con la regla del producto:

\[ \dfrac{d}{dx}[f(x)g(x)]=f′(x)g(x)+f(x)g′(x). \nonumber \]

Coincidencia término por término da\( y=f(x),g(x)=μ(x)\), y\( g′(x)=μ(x)p(x)\). Tomando la derivada de\( g(x)=μ(x)\) y fijándola igual al lado derecho de los\( g′(x)=μ(x)p(x)\) leads a

\[ μ′(x)=μ(x)p(x). \nonumber \]

Esta es una ecuación diferencial separable de primer orden para\(μ(x).\) Sabemos\( p(x)\) porque aparece en la ecuación diferencial que estamos resolviendo. Separación de variables e integración de rendimientos

\[ \begin{align} \dfrac{μ′(x)}{μ(x)} =p(x) \\[4pt] ∫\dfrac{μ′(x)}{μ(x)}dx =∫p(x)dx \\[4pt] \ln|μ(x)| =∫p(x)dx+C \\[4pt] e^{\ln|μ(x)|} =e^{∫p(x)dx+C} \\[4pt] |μ(x)| =C_1e^{∫p(x)dx} \\[4pt] μ(x) =C_2e^{∫p(x)dx}. \end{align} \nonumber \]

Aquí\( C_2\) puede haber una constante arbitraria (positiva o negativa). Esto conduce a un método general para resolver una ecuación diferencial lineal de primer orden. Primero multiplicamos ambos lados de la ecuación por el factor integrador\( μ(x).\) Esto da

\[ μ(x)y′+μ(x)p(x)y=μ(x)q(x). \label{Deq5} \]

El lado izquierdo de la Ecuación\ ref {Deq5} se puede reescribir como\( \dfrac{d}{dx}(μ(x)y)\).

\[ \dfrac{d}{dx}(μ(x)y)=μ(x)q(x). \label{Deq6} \]

Siguiente integrar ambos lados de la Ecuación\ ref {Deq6} con respecto a\(x\).

\[ \begin{align} ∫\dfrac{d}{dx}(μ(x)y)dx =∫μ(x)q(x)dx \\[4pt] μ(x)y =∫μ(x)q(x)dx \label{Deq7} \end{align} \]

Divide ambos lados de la Ecuación\ ref {Deq6} por\( μ(x)\):

\[ y=\dfrac{1}{μ(x)}\left[∫μ(x)q(x)dx+C\right]. \nonumber \]

Ya que\( μ(x)\) se calculó anteriormente, ahora estamos terminados. Una nota importante sobre la constante integradora\( C\): Puede parecer que somos inconsistentes en el uso de la constante integradora. Sin embargo, la involucración integral\( p(x)\) es necesaria para encontrar un factor integrador para la Ecuación. Solo se necesita un factor integrador para resolver la ecuación; por lo tanto, es seguro asignar un valor\(C\) para esta integral. Elegimos\(C=0\). Al calcular la integral dentro de los corchetes en Ecuación, es necesario mantener nuestras opciones abiertas para el valor de la constante de integración, porque nuestro objetivo es encontrar una familia general de soluciones a Ecuación. Este factor integrador garantiza precisamente eso.

Estrategia de resolución de problemas: resolución de una ecuación diferencial lineal de primer orden

1. Poner la ecuación en forma estándar e identificar\( p(x)\) y\( q(x)\).
2. Calcular el factor de integración\[ μ(x)=e^{∫p(x)dx}. \nonumber \]
3. Multiplique ambos lados de la ecuación diferencial por\( μ(x)\).
4. Integrar ambos lados de la ecuación obtenida en paso\( 3\), y dividir ambos lados por\( μ(x)\).
5. Si hay una condición inicial, determinar el valor de\( C\).

Ejemplo\( \PageIndex{2}\): Solving a First-order Linear Equation

Encuentre una solución general para la ecuación diferencial\( xy'+3y=4x^2−3x.\) Supongamos\( x>0.\)

Solución

1. Para poner esta ecuación diferencial en forma estándar, divida ambos lados por\( x\):

\[ y'+\dfrac{3}{x}y=4x−3. \nonumber \]

Por lo tanto\( p(x)=\dfrac{3}{x}\) y\( q(x)=4x−3.\)

2. El factor integrador es\( μ(x)=e^{∫(3/x)}dx=e^{3 \ln x}=x^3\).

3. Multiplicar ambos lados de la ecuación diferencial por nos\( μ(x)\) da

\[ \begin{align*} x^3y′+x^3(\dfrac{3}{x}) =x^3(4x−3) \\[4pt] x^3y′+3x^2y =4x^4−3x^3 \\[4pt] \dfrac{d}{dx}(x^3y) = 4x^4−3x^3. \end{align*}\]

4. Integrar ambos lados de la ecuación.

\[ \begin{align*} ∫\dfrac{d}{dx}(x^3y)dx = ∫4x^4−3x^3dx \\[4pt] x^3y =\dfrac{4x^5}{5}−\dfrac{3x^4}{4}+C \\[4pt] y =\dfrac{4x^2}{5}−\dfrac{3x}{4}+Cx^{−3}. \end{align*}\]

5. No hay valor inicial, por lo que el problema está completo.

Análisis

Es posible que hayas notado la condición que se impuso a la ecuación diferencial; es decir,\( x>0\). Para cualquier valor distinto de cero de\( C\), la solución general no se define en\( x=0\). Además, cuando\( x<0\), el factor integrador cambia. El factor integrador viene dado por la Ecuación como\( f(x)=e^{∫p(x)dx}\). Para ello\( p(x)\) conseguimos

\[ \begin{align*} e^{∫p(x)dx} =e^{∫(3/x)dx} \\[4pt] =e^{3\ln|x|} \\[4pt] =|x|^3 \end{align*}\]

ya que\(x<0\). El comportamiento de la solución general cambia en\( x=0\) gran parte debido a que ahí no\( p(x)\) se define.

Ejercicio\(\PageIndex{2}\)

Encuentra la solución general a la ecuación diferencial\( (x−2)y'+y=3x^2+2x.\) Asumir\( x>2\).

Pista

Utilice el método descrito en la estrategia de resolución de problemas para ecuaciones diferenciales lineales de primer orden.

Contestar

\( y=\dfrac{x^3+x^2+C}{x−2}\)

Ahora usamos la misma estrategia para encontrar la solución a un problema de valor inicial.

Ejemplo\( \PageIndex{3}\): A First-order Linear Initial-Value Problem

Resolver el problema del valor inicial

\[ y′+3y=2x−1,y(0)=3. \nonumber \]

Solución

1. Esta ecuación diferencial ya está en forma estándar con\( p(x)=3\) y\( q(x)=2x−1\).

2. El factor integrador es\( μ(x)=e^{∫3dx}=e^{3x}\).

3. Multiplicar ambos lados de la ecuación diferencial por\( μ(x)\) da

\[ \begin{align*} e^{3x}y′+3e^{3x}y =(2x−1)e^{3x} \\[4pt] \dfrac{d}{dx}[ye^{3x}] =(2x−1)e^{3x}. \end{align*}\]

Integrar ambos lados de la ecuación:

\( ∫\dfrac{d}{dx}[ye^{3x}]dx=∫(2x−1)e^{3x}dx\)

\( ye^{3x}=\dfrac{e^{3x}}{3}(2x−1)−∫\dfrac{2}{3}e^{3x}dx\)

\( ye^{3x}=\dfrac{e^{3x}(2x−1)}{3}−\dfrac{2e^{3x}}{9}+C\)

\( y=\dfrac{2x−1}{3}−\dfrac{2}{9}+Ce^{−3x}\)

\( y=\dfrac{2x}{3}−\dfrac{5}{9}+Ce^{−3x}\).

4. Ahora sustituya\( x=0\) y\( y=3\) en la solución general y resuelva por\( C\):

\[ \begin{align*} y =\dfrac{2}{3}x−\dfrac{5}{9}+Ce^{−3x} \\[4pt] 3 =\dfrac{2}{3}(0)−\dfrac{5}{9}+Ce^{−3(0)} \\[4pt] 3 =−\dfrac{5}{9}+C \\[4pt] C=\dfrac{32}{9}. \end{align*}\]

Por lo tanto, la solución al problema del valor inicial es

\[ y=\dfrac{2}{3}x−\dfrac{5}{9}+\dfrac{32}{9}e^{−3x}. \nonumber \]

Ejemplo\(\PageIndex{4}\):

Resolver el problema del valor inicial\[ y'−2y=4x+3y(0)=−2. \nonumber \]

Solución

\[ y=−2x−4+2e^{2x} \nonumber \]

Aplicaciones de Ecuaciones Diferenciales Lineales de Primer Orden

Analizamos dos aplicaciones diferentes de ecuaciones diferenciales lineales de primer orden. El primero involucra la resistencia al aire ya que se relaciona con objetos que están subiendo o bajando; el segundo involucra un circuito eléctrico. Otras aplicaciones son numerosas, pero la mayoría se resuelven de manera similar.

Caída libre con resistencia al aire

Discutimos la resistencia al aire al inicio de esta sección. El siguiente ejemplo muestra cómo aplicar este concepto para una pelota en movimiento vertical. Otros factores pueden afectar la fuerza de la resistencia al aire, como el tamaño y la forma del objeto, pero aquí los ignoramos.

Ejemplo\( \PageIndex{5}\): A Ball with Air Resistance

Una raquetball es golpeada recta hacia arriba con una velocidad inicial de\( 2\) m/s. La masa de una raquetball es de aproximadamente\( 0.0427\) kg. La resistencia al aire actúa sobre la pelota con una fuerza numéricamente igual a\( 0.5v\), donde\( v\) representa la velocidad de la pelota en el momento\( t\).

1. Encuentra la velocidad de la pelota en función del tiempo.
2. ¿Cuánto tiempo tarda la pelota en alcanzar su máxima altura?
3. Si la pelota es golpeada desde una altura inicial de\( 1\) metro, ¿qué tan alto alcanzará?

Solución

a. La masa\( m=0.0427kg,k=0.5,\) y\( g=9.8m/s^2\). La velocidad inicial es\( v_0=2 m/s\). Por lo tanto, el problema del valor inicial es

\( 0.0427\dfrac{dv}{dt}=−0.5v−0.0427(9.8),v_0=2.\)

Dividiendo la ecuación diferencial por\( 0.0427\) da

\( \dfrac{dv}{dt}=−11.7096v−9.8,v_0=2.\)

La ecuación diferencial es lineal. Usando la estrategia de resolución de problemas para ecuaciones diferenciales lineales:

Paso 1. Reescribir la ecuación diferencial como\( \dfrac{dv}{dt}+11.7096v=−9.8\). Esto da\( p(t)=11.7096\) y\( q(t)=−9.8\)

Paso 2. El factor integrador es\( μ(t)=e^{∫11.7096dt}=e^{11.7096t}.\)

Paso 3. Multiplica la ecuación diferencial por\( μ(t)\):

\( e^{11.7096t\dfrac{dv}{dt}}+11.7096ve^{11.7096t}=−9.8e^{11.7096t}\)

\( \dfrac{d}{dt}[ve^{11.7096t}]=−9.8e^{11.7096t}.\)

Paso 4. Integrar ambos lados:

\( ∫\dfrac{d}{dt}[ve^{11.7096t}]dt=∫−9.8e^{11.7096t}dt\)

\( ve^{11.7096t}=\dfrac{−9.8}{11.7096}e^{11.7096t}+C\)

\( v(t)=−0.8369+Ce^{−11.7096t}.\)

Paso 5. Resuelva para\( C\) usar la condición inicial\( v_0=v(0)=2\):

\( v(t)=−0.8369+Ce^{−11.7096t}\)

\( v(0)=−0.8369+Ce^{−11.7096(0)}\)

\( 2=−0.8369+C\)

\( C=2.8369.\)

Por lo tanto, la solución al problema del valor inicial es

\( v(t)=2.8369e^{−11.7096t}−0.8369.\)

b. La bola alcanza su altura máxima cuando la velocidad es igual a cero. El motivo es que cuando la velocidad es positiva, está subiendo, y cuando es negativa, está cayendo. Por lo tanto, cuando es cero, no está subiendo ni bajando, y está a su altura máxima:

\( 2.8369e^{−11.7096t}−0.8369=0\)

\( 2.8369e^{−11.7096t}=0.8369\)

\( e^{−11.7096t}=\dfrac{0.8369}{2.8369}≈0.295\)

\( lne^{−11.7096t}=ln0.295≈−1.221\)

\( −11.7096t=−1.221\)

\( t≈0.104.\)

Por lo tanto, se tarda aproximadamente\( 0.104\) segundos en alcanzar la altura máxima.

c. Para encontrar la altura de la pelota en función del tiempo, utilice el hecho de que la derivada de la posición es la velocidad, es decir, si\( h(t)\) representa la altura en el tiempo\( t\), entonces\( h′(t)=v(t)\). Porque sabemos\( v(t)\) y la altura inicial, podemos formar un problema de valor inicial:

\( h′(t)=2.8369e^{−11.7096t}−0.8369,h(0)=1.\)

Integrando ambos lados de la ecuación diferencial con respecto a\( t\) da

\( ∫h′(t)dt=∫2.8369e^{−11.7096t}−0.8369dt\)

\( h(t)=−\dfrac{2.8369}{11.7096}e^{−11.7096t}−0.8369t+C\)

\( h(t)=−0.2423e^{−11.7096t}−0.8369t+C.\)

Resolver\( C\) por usando la condición inicial:

\( h(t)=−0.2423e^{−11.7096t}−0.8369t+C\)

\( h(0)=−0.2423e^{−11.7096(0)}−0.8369(0)+C\)

\( 1=−0.2423+C\)

\( C=1.2423.\)

Por lo tanto

\( h(t)=−0.2423e^{−11.7096t}−0.8369t+1.2423.\)

Después del\( 0.104\) segundo, la altura viene dada por

\( h(0.2)=−0.2423e^{−11.7096t}−0.8369t+1.2423≈1.0836\)medidor.

Ejercicio\(\PageIndex{3}\)

El peso de un centavo es de\(2.5\) gramos (United States Mint, “Coin Especificaciones”, consultado el 9 de abril de 2015, http://www.usmint.gov/about_the_mint...specifications), y la plataforma de observación superior del Empire State Building está\( 369\) a metros sobre la calle. Dado que el centavo es un objeto pequeño y relativamente liso, la resistencia al aire que actúa sobre el centavo es en realidad bastante pequeña. Suponemos que la resistencia del aire es numéricamente igual a\( 0.0025v\). Además, el centavo se baja sin que se le imparta velocidad inicial.

1. Configura un problema de valor inicial que represente el centavo que cae.
2. Resolver el problema para\( v(t)\).
3. ¿Cuál es la velocidad terminal del centavo (es decir, calcular el límite de la velocidad a medida que se\( t\) acerca al infinito)?

Pista

Configure la ecuación diferencial de la misma manera que Ejemplo. Recuerda convertir de gramos a kilogramos.

Contestar

a.\( \dfrac{dv}{dt}=−v−9.8\)\( v(0)=0\)

b.\( v(t)=9.8(e^{−t}−1)\)

c.\( \lim_{t→∞}v(t)=\lim_{t→∞}(9.8(e^{−t}−1))=−9.8m/s≈−21.922mph\)

Circuitos Eléctricos

Una fuente de fuerza electromotriz (por ejemplo, una batería o generador) produce un flujo de corriente en un circuito cerrado, y esta corriente produce una caída de voltaje a través de cada resistor, inductor y condensador en el circuito. La regla de bucle de Kirchhoff establece que la suma de las caídas de voltaje a través de resistencias, inductores y condensadores es igual a la fuerza electromotriz total en un circuito cerrado. Tenemos los siguientes tres resultados:

1. La caída de voltaje a través de una resistencia viene dada por

\( E_R=Ri,\)

donde\( R\) es una constante de proporcionalidad llamada resistencia, y\( i\) es la corriente.

2. La caída de voltaje a través de un inductor viene dada por

\( EL=Li′\),

donde\( L\) es una constante de proporcionalidad llamada inductancia, y denota\( i\) nuevamente la corriente.

3. La caída de voltaje a través de un condensador viene dada por

\( E_C=\dfrac{1}{C}q\),

donde\( C\) es una constante de proporcionalidad llamada capacitancia, y\( q\) es la carga instantánea en el condensador. La relación entre\( i\) y\( q\) es\( i=q′\).

Utilizamos unidades de voltios\( (V)\) para medir voltaje\( E\), amperios\( (A)\) para medir corriente\( i\), culombios\( (C)\) para medir carga\( q\), ohmios\( (Ω)\) para medir resistencia\( R\), henrys\( (H)\) para medir inductancia\( L\) y faradios\( (F)\) para medir capacitancia\( C\). Considera el circuito en la Figura\( \PageIndex{2}\).

Figura\( \PageIndex{2}\): Un circuito eléctrico típico, que contiene un generador de voltaje\( (V_S)\)\( (C)\), condensador\( (L)\), inductor y resistencia\( (R)\).

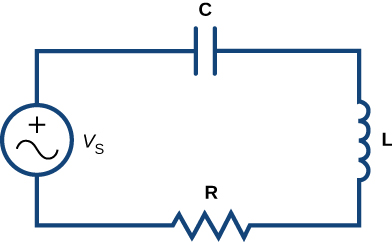
Aplicando la Regla de Bucle de Kirchhoff a este circuito, dejamos\( E\) denotar la fuerza electromotriz suministrada por el generador de voltaje. Entonces

\( E_L+E_R+E_C=E\).

Sustituyendo las expresiones por\( E_L,E_R,\) y\( E_C\) en esta ecuación, obtenemos

\( Li′+Ri+\dfrac{1}{C}q=E.\)

Si no hay condensador en el circuito, entonces la ecuación se convierte

\( Li′+R_i=E.\)

Esta es una ecuación diferencial de primer orden en\( i\). El circuito se conoce como un\( LR\) circuito.

A continuación, supongamos que no hay inductor en el circuito, pero hay un condensador y una resistencia, así\( L=0,R≠0,\) y\( C≠0.\) Entonces la ecuación se puede reescribir como

\( Rq′+\dfrac{1}{C}q=E,\)

que es una ecuación diferencial lineal de primer orden. Esto se conoce como un circuito RC. En cualquier caso, podemos configurar y resolver un problema de valor inicial.

Circuito eléctrico

Un circuito tiene en serie una fuerza electromotriz dada por\( E=50\sin 20tV,\) una resistencia de\( 5Ω\), y un inductor de\( 0.4H\). Si la corriente inicial es\( 0\), busque la corriente en el momento\( t>0\).

Solución

Tenemos una resistencia y un inductor en el circuito, por lo que usamos Ecuación. La caída de voltaje a través de la resistencia viene dada por\( E_R=R_i=5_i\). La caída de voltaje a través del inductor viene dada por\( E_L=Li′=0.4i′\). La fuerza electromotriz se convierte en el lado derecho de la Ecuación. Por lo tanto, la ecuación

\[ 0.4i′+5i=50\sin 20t. \nonumber \]

Dividir ambos lados por\( 0.4\) da la ecuación

\[ i′+12.5i=125\sin 20t. \nonumber \]

Dado que la corriente inicial es 0, este resultado da una condición inicial de\( i(0)=0.\) Podemos resolver este problema de valor inicial utilizando la estrategia de cinco pasos para resolver ecuaciones diferenciales de primer orden.

Paso 1. Reescribir la ecuación diferencial como\( i′+12.5i=125\sin 20t\). Esto da\( p(t)=12.5\) y\( q(t)=125\sin 20t\).

Paso 2. El factor integrador es\( μ(t)=e^{∫12.5dt}=e^{12.5t}\).

Paso 3. Multiplica la ecuación diferencial por\( μ(t)\):

\( e^{12.5t}i′+12.5e^{12.5t}i=125e^{12.5t}\sin 20t\)

\( \dfrac{d}{dt}[ie^{12.5}t]=125e^{12.5t}\sin 20t\).

Paso 4. Integrar ambos lados:

\( ∫\dfrac{d}{dt}[ie^{12.5t}]dt=∫125e^{12.5t}\sin 20tdt\)

\( ie^{12.5t}=(\dfrac{250\sin 20t−400\cos 20t}{89})e^{12.5t}+C\)

\( i(t)=\dfrac{250\sin 20t−400\cos 20t}{89}+Ce^{−12.5t}\).

Paso 5. Resuelva para\( C\) usar la condición inicial\( v(0)=2\):

\( i(t)=\dfrac{250\sin 20t−400\cos 20t}{89}+Ce^{−12.5t}\)

\( i(0)=\dfrac{250sin20(0)−400cos20(0)}{89}+Ce^{−12.5(0)}\)

\( 0=−\dfrac{400}{89}+C\)

\( C=\dfrac{400}{89}\).

Por lo tanto, la solución al problema del valor inicial es

\[ i(t)=\dfrac{250\sin 20t−400\cos 20t+400e^{−12.5t}}{89}=\dfrac{250\sin 20t−400\cos 20t}{89}+\dfrac{400e^{−12.5t}}{89}. \nonumber \]

El primer término se puede reescribir como una sola función coseno. Primero, multiplica y divide por\( \sqrt{250^2+400^2}=50\sqrt{89}\):

\( \dfrac{250\sin 20t−400\cos 20t}{89}=\dfrac{50\sqrt{89}}{89}(\dfrac{250\sin 20t−400\cos 20t}{50\sqrt{89}})=−\dfrac{50\sqrt{89}}{89}(\dfrac{8\cos 20t}{\sqrt{89}}−\dfrac{5\sin 20t}{\sqrt{89}})\).

A continuación,\( φ\) definir como un ángulo agudo tal que\( \cos φ=\dfrac{8}{\sqrt{89}}\). Entonces\( \sin φ=\dfrac{5}{\sqrt{89}}\) y

\( −\dfrac{50\sqrt{89}}{89}(\dfrac{8\cos 20t}{\sqrt{89}}−\dfrac{5\sin 20t}{\sqrt{89}})=−\dfrac{50\sqrt{89}}{89}(\cos φ\cos 20t−\sin φ\sin 20t)=−\dfrac{50\sqrt{89}}{89}\cos(20t+φ).\)

Por lo tanto, la solución puede escribirse como

\( i(t)=−\dfrac{50\sqrt{89}}{89}cos(20t+φ)+\dfrac{400e^{−12.5t}}{89}\).

Al segundo término se le llama término de atenuación, porque desaparece rápidamente a medida que se\( t\) hace más grande. El desplazamiento de fase viene dado por\( φ\), y la amplitud de la corriente de estado estacionario viene dada por\( \dfrac{50\sqrt{89}}{89}\). La gráfica de esta solución aparece en la Figura\( \PageIndex{3}\):

Figura\( \PageIndex{3}\).

Ejercicio\(\PageIndex{4}\)

Un circuito tiene en serie una fuerza electromotriz dada por\( E=20sin5t\) V, un condensador con capacitancia\( 0.02F\), y una resistencia de\( 8Ω\). Si el cargo inicial es\( 4C\), encuentra el cargo a la hora\( t>0\).

Pista

Use Ecuación para un\( RC\) circuito para configurar un problema de valor inicial.

Contestar

Problema de valor inicial:

\( 8q′+\dfrac{1}{0.02}q=20sin5t,q(0)=4\)

\( q(t)=\dfrac{10sin5t−8cos5t+172e^{−6.25t}}{41}\)

Conceptos clave

• Cualquier ecuación diferencial lineal de primer orden se puede escribir en la forma\( y'+p(x)y=q(x)\).
• Podemos usar una estrategia de resolución de problemas de cinco pasos para resolver una ecuación diferencial lineal de primer orden que puede o no incluir un valor inicial.
• Las aplicaciones de ecuaciones diferenciales lineales de primer orden incluyen determinar el movimiento de un objeto ascendente o descendente con resistencia al aire y encontrar corriente en un circuito eléctrico.

Ecuaciones Clave

• forma estándar

\( y'+p(x)y=q(x)\)

• factor de integración

\( μ(x)=e^{∫p(x)dx}\)

Glosario

factor de integración

cualquier función\(f(x)\) que se multiplica en ambos lados de una ecuación diferencial para hacer que el lado que involucra la función desconocida sea igual a la derivada de un producto de dos funciones

lineal

descripción de una ecuación diferencial de primer orden que se puede escribir en la forma\( a(x)y′+b(x)y=c(x)\)

forma estándar

la forma de una ecuación diferencial lineal de primer orden obtenida escribiendo la ecuación diferencial en la forma\( y'+p(x)y=q(x)\)