8.6: Capítulo 8 Ejercicios de revisión

Última actualización
Guardar como PDF

Page ID: 116252

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

¿Verdadero o Falso? Justifica tu respuesta con una prueba o un contraejemplo.

1) La ecuación diferencial$y'=3x^2y−\cos(x)y''$ es lineal.

2) La ecuación diferencial$y'=x−y$ es separable.

Contestar: $F$

3) Se pueden resolver explícitamente todas las ecuaciones diferenciales de primer orden por separación o por el método de integración de factores.

4) Se puede determinar el comportamiento de todas las ecuaciones diferenciales de primer orden utilizando campos direccionales o el método de Euler.

Contestar: $T$

Para los siguientes problemas, encuentre la solución general a las ecuaciones diferenciales.

5)$y′=x^2+3e^x−2x$

6)$y'=2^x+\cos^{−1}x$

Contestar: $y(x)=\frac{2^x}{ln(2)}+xcos^{−1}x−\sqrt{1−x^2}+C$

7)$y'=y(x^2+1)$

8)$y'=e^{−y}\sin x$

Contestar: $y(x)=\ln(C−\cos x)$

9)$y'=3x−2y$

10)$y'=y\ln y$

Contestar: $y(x)=e^{e^{C+x}}$

Para los siguientes problemas, encuentre la solución al problema de valor inicial.

11)$y'=8x−\ln x−3x^4, \quad y(1)=5$

12)$y'=3x−\cos x+2, \quad y(0)=4$

Contestar: $y(x)=4+\frac{3}{2}x^2+2x−\sin x$

13)$xy'=y(x−2), \quad y(1)=3$

14)$y'=3y^2(x+\cos x), \quad y(0)=−2$

Contestar: $y(x)=−\dfrac{2}{1+3(x^2+2\sin x)}$

15)$(x−1)y'=y−2, \quad y(0)=0$

16)$y'=3y−x+6x^2, \quad y(0)=−1$

Contestar: $y(x)=−2x^2−2x−\frac{1}{3}−\frac{2}{3}e^{3x}$

Para los siguientes problemas, dibuje el campo direccional asociado a la ecuación diferencial, luego resuelva la ecuación diferencial. Dibuje una solución de muestra en el campo direccional.

17)$y'=2y−y^2$

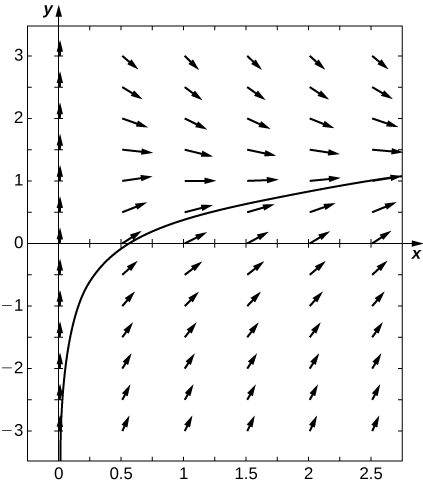
18)$y'=\dfrac{1}{x}+\ln x−y,$ para$x>0$

Contestar

$y(x)=Ce^{−x}+\ln x$

$Un campo de dirección con flechas apuntando hacia arriba y hacia la derecha a lo largo de una curva logarítmica que se acerca al infinito negativo cuando x va a cero y aumenta a medida que x va al infinito.$

Para los siguientes problemas, use el Método de Euler con$n=5$ pasos sobre el intervalo$t=[0,1].$ Luego resuelva exactamente el problema del valor inicial. ¿Qué tan cerca está tu estimación del Método de Euler?

19)$y'=−4yx, \quad y(0)=1$

20)$y'=3^x−2y, \quad y(0)=0$

Contestar: Euler:$0.6939$, Solución
exacta:$y(x)=\dfrac{3^x−e^{−2x}}{2+\ln(3)}$

Para los siguientes problemas, configurar y resolver las ecuaciones diferenciales.

21) Un automóvil circula por una autopista, acelerando según$a=5\sin(πt),$ donde$t$ representa el tiempo en minutos. Encuentra la velocidad en cualquier momento$t$, asumiendo que el auto arranca con una velocidad inicial de$60$ mph.

22) Lanza una bola de$2$ kilogramos de masa al aire con una velocidad ascendente de$8$ m/s Encuentra exactamente el tiempo en que la pelota permanecerá en el aire, asumiendo que la gravedad viene dada por$g=9.8\,\text{m/s}^2$.

Contestar: $\frac{40}{49}$segundo

23) Se cae una pelota con una masa de$5$ kilogramos por la ventana de un avión a una altura de$5000$ m. ¿Cuánto tiempo tarda la pelota en llegar al suelo?

24) Se cae la misma bola de$5$ kilogramos de masa fuera de la misma ventana del avión a la misma altura, excepto que esta vez asumes una fuerza de arrastre proporcional a la velocidad de la pelota, utilizando una constante de proporcionalidad de$3$ y la bola alcanza la velocidad terminal. Resuelve por la distancia caída en función del tiempo. ¿Cuánto tiempo tarda la pelota en llegar al suelo?

Contestar: $x(t)=5000+\frac{245}{9}−\frac{49}{3}t−\frac{245}{9}e^{−5/3t}, \quad t=307.8$segundos

25) Un medicamento se administra a un paciente cada$24$ hora y se limpia a una velocidad proporcional a la cantidad de fármaco que queda en el cuerpo, con proporcionalidad constante$0.2$. Si el paciente necesita un nivel basal de$5$ mg para estar en el torrente sanguíneo en todo momento, ¿qué tan grande debe ser la dosis?

26) Un tanque$1000$ de litro contiene agua pura y una solución de$0.2$ kg de sal/L se bombea al tanque a una velocidad de$1$ L/min y se drena a la misma velocidad. Resuelve la cantidad total de sal en el tanque a la vez$t$.

Contestar: $T(t)=200\left(1−e^{−t/1000}\right)$

27) Hervir agua para hacer el té. Cuando viertes el agua en tu tetera, la temperatura es$100°C.$ Después de$5$ minutos en tu$15°C$ habitación, la temperatura del té es$85°C$. Resolver la ecuación para determinar las temperaturas del té a la vez$t$. ¿Cuánto tiempo debes esperar hasta que el té esté a una temperatura bebible ($72°C$)?

28) La población humana (en miles) de Nevada en$1950$ era aproximadamente$160$. Si la capacidad de carga se estima en$10$ millones de individuos, y asumiendo una$2\%$ tasa de crecimiento anual, desarrollar un modelo de crecimiento logístico y resolver para la población de Nevada en cualquier momento (usar$1950$ como tiempo = 0). ¿Para qué población predice tu modelo$2000$? ¿Qué tan cerca está su predicción del verdadero valor de$1,998,257$?

Contestar: $P(t)=\dfrac{1600000e^{0.02t}}{9840+160e^{0.02t}}$

29) Repetir el problema anterior pero utilizar el modelo de crecimiento Gompertz. ¿Cuál es más exacto?