9.5E: Ejercicios para la Sección 9.5

En los ejercicios 1 - 30, indique si cada una de las siguientes series converge absoluta, condicionalmente, o no en absoluto.

1)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{n+3}\)

2)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{\sqrt{n}+1}{\sqrt{n}+3}\)

Responder

Esta serie diverge por la prueba de divergencia. Los términos no tienden a cero.

3)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{1}{\sqrt{n+3}}\)

4)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{\sqrt{n+3}}{n}\)

Responder

Converge condicionalmente alternando la prueba en serie, ya que\(\sqrt{n+3}/n\) es decreciente y su límite es 0. No converge absolutamente en comparación con\(p\) -series,\(p=1/2\).

5)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{1}{n!}\)

6)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{3^n}{n!}\)

Responder

Converge absolutamente por comparación límite a\(3^n/4^n,\) por ejemplo.

7)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{n−1}{n}\right)^n\)

8)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{n+1}{n}\right)^n\)

Responder

Diverge por prueba de divergencia desde\(\displaystyle \lim_{n→∞}|a_n|=e\) y no\(0\).

9)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\sin^2n\)

10)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\cos^2n\)

Responder

Diverge por la prueba de divergencia, ya que sus términos no tienden a cero. El límite de la secuencia de sus términos no existe.

11)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\sin^2(1/n)\)

12)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\cos^2(1/n)\)

Responder

\(\displaystyle \lim_{n→∞}\cos^2(1/n)=1.\)Diverge por prueba de divergencia.

13)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\ln(1/n)\)

14)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\ln(1+\frac{1}{n})\)

Responder

Converge por prueba en serie alternada.

15)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n^2}{1+n^4}\)

16)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n^e}{1+n^π}\)

Responder

Converge condicionalmente por prueba en serie alterna. No converge absolutamente por comparación límite con\(p\) -series,\(p=π−e\)

Solución:

17)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}2^{1/n}\)

18)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}n^{1/n}\)

Responder

Diverge; los términos no tienden a cero.

19)\(\displaystyle \sum^∞_{n=1}(−1)^n(1−n^{1/n})\) (Pista:\(n^{1/n}≈1+\ln(n)/n\) para grandes\(n\).)

20)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}n\left(1−\cos\left(\frac{1}{n}\right)\right)\) (Pista:\(\cos(1/n)≈1−1/n^2\) para grandes\(n\).)

Responder

Converge por prueba en serie alternada. No converge absolutamente por comparación límite con series armónicas.

21)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}(\sqrt{n+1}−\sqrt{n})\) (Pista: Racionalizar el numerador.)

22)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{1}{\sqrt{n}}−\frac{1}{\sqrt{n+1}}\right)\) (Pista: Multiplicar cruzadamente y luego racionalizar el numerador.)

Responder

Converge absolutamente por comparación límite con\(p\) -series,\(p=3/2\), después de aplicar la pista.

23)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}(\ln(n+1)−\ln n)\)

24)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}n(\tan^{−1}(n+1)−\tan^{−1}n)\) (Pista: Usar el Teorema del Valor Medio.)

Responder

Converge alternando la prueba de serie ya que\( n(\tan^{−1}(n+1)−\tan^{−1}n)\) está disminuyendo a cero para grandes\(n\) .No converge absolutamente por comparación límite con series armónicas después de aplicar pista.

25)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}((n+1)^2−n^2)\)

26)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{1}{n}−\frac{1}{n+1}\right)\)

Responder

Converge absolutamente, ya que\( a_n=\dfrac{1}{n}−\dfrac{1}{n+1}\) son términos de una serie telescópica.

27)\(\displaystyle \sum^∞_{n=1}\frac{\cos(nπ)}{n}\)

28)\(\displaystyle \sum^∞_{n=1}\frac{\cos(nπ)}{n^{1/n}}\)

Responder

Los términos no tienden a cero. Las series divergen por prueba de divergencia.

29)\(\displaystyle \sum^∞_{n=1}\frac{1}{n}\sin(\frac{nπ}{2})\)

30)\(\displaystyle \sum^∞_{n=1}\sin(nπ/2)\sin(1/n)\)

Responder

Converge por prueba en serie alternada. No converge absolutamente por comparación límite con series armónicas.

En los ejercicios 31 - 36, utilice la estimación\(|R_N|≤b_{N+1}\) para encontrar un valor de\(N\) que garantice que la suma de los primeros\(N\) términos de la serie alterna\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}b_n\) difiera de la suma infinita por como mucho el error dado. Calcular la suma parcial\(S_N\) para esto\(N\).

31) [T]\(b_n=1/n,\) error\( <10^{−5}\)

32) [T]\(b_n=1/\ln(n), n≥2,\) error\(<10^{−1}\)

Responder

\( \ln(N+1)>10, N+1>e^{10}, N≥22026; S_{22026}=0.0257…\)

33) [T]\(b_n=1/\sqrt{n},\) error\(<10^{−3}\)

34) [T]\(b_n=1/2^n\), error\(<10^{−6}\)

Responder

\(2^{N+1}>10^6\)o\(N+1>6\ln(10)/\ln(2)=19.93.\) o\(N≥19; S_{19}=0.333333969…\)

35) [T]\(b_n=ln(1+\dfrac{1}{n}),\) error\( <10^{−3}\)

36) [T]\(b_n=1/n^2,\) error\(<10^{−6}\)

Responder

\((N+1)^2>10^6\)o\(N>999; S_{1000}≈0.822466.\)

Para los ejercicios 37 - 45, indique si cada una de las siguientes afirmaciones es verdadera o falsa. Si la declaración es falsa, proporcione un ejemplo en el que sea falsa.

37) Si\( b_n≥0\) es decreciente y\(\displaystyle \lim_{n→∞}b_n=0\), entonces\(\displaystyle \sum_{n=1}^∞(b_{2n−1}−b_{2n})\) converge absolutamente.

38) Si\( b_n≥0\) está disminuyendo, entonces\(\displaystyle \sum_{n=1}^∞(b_{2n−1}−b_{2n})\) converge absolutamente.

Contestar

Cierto. \(b_n\)no es necesario tender a cero ya que si\(\displaystyle c_n=b_n−\lim b_n\), entonces\(c_{2n−1}−c_{2n}=b_{2n−1}−b_{2n}.\)

39) Si\( b_n≥0\) y\(\displaystyle \lim_{n→∞}b_n=0\) luego\(\displaystyle \sum_{n=1}^∞(\frac{1}{2}(b_{3n−2}+b_{3n−1})−b_{3n})\) converge.

40) Si\(b_n≥0\) es decreciente y\(\displaystyle \sum_{n=1}^∞(b_{3n−2}+b_{3n−1}−b_{3n})\) converge entonces\(\displaystyle \sum_{n=1}^∞b_{3n−2}\) converge.

Contestar

Cierto. \(b_{3n−1}−b_{3n}≥0,\)por lo que la convergencia de\(\displaystyle \sum b_{3n−2}\) sigue de la prueba de comparación.

41) Si\(b_n≥0\) está disminuyendo y\(\displaystyle \sum_{n=1}^∞(−1)^{n−1}b_n\) converge condicionalmente pero no absolutamente, entonces\(b_n\) no tiende a cero.

42) Dejar\(a^+_n=a_n\) si\(a_n≥0\) y\( a^−_n=−a_n\) si\(a_n<0\). (También,\( a^+_n=0\) si\(a_n<0\) y\(a^−_n=0\) si\(a_n≥0\).) Si\(\displaystyle \sum_{n=1}^∞a_n\) converge condicionalmente pero no absolutamente, entonces ni\(\displaystyle \sum_{n=1}^∞a^−_n\) convergen\(\displaystyle \sum_{n=1}^∞a^+_n\) ni convergen.

Contestar

Cierto. Si uno converge, entonces también debe hacerlo el otro, implicando convergencia absoluta.

43) Supongamos que\(a_n\) es una secuencia de números reales positivos y que\(\displaystyle \sum_{n=1}^∞a_n\) converge.

44) Supongamos que\(b_n\) es una secuencia arbitraria de unos y menos unos. ¿Converge\(\displaystyle \sum_{n=1}^∞a_nb_n\) necesariamente?

45) Supongamos que\(a_n\) es una secuencia tal que\(\displaystyle \sum_{n=1}^∞a_nb_n\) converge para cada secuencia posible\(b_n\) de ceros y unos. ¿\(\displaystyle \sum_{n=1}^∞a_n\)Converge absolutamente?

Contestar

Sí. Tomar\(b_n=1\) si\(a_n≥0\) y\( b_n=0\) si\(a_n<0\). Entonces\(\displaystyle \sum_{n=1}^∞a_nb_n=\sum_{n:a_n≥0}a_n\) converge. De igual manera, se puede mostrar\(\displaystyle \sum_{n:a_n<0}a_n\) converge. Dado que ambas series convergen, la serie debe converger absolutamente.

En los ejercicios 46 - 49, las series no satisfacen las hipótesis de la prueba de series alternas como se indica. En cada caso, exponer qué hipótesis no está satisfecha. Determinar si la serie converge absolutamente.

46)\(\displaystyle \sum_{n=1}^∞(−1)^{n+1}\frac{\sin^2n}{n}\)

47)\(\displaystyle \sum_{n=1}^∞(−1)^{n+1}\frac{\cos^2n}{n}\)

Contestar

No decreciente. No converge absolutamente.

48)\(\displaystyle 1+\frac{1}{2}−\frac{1}{3}−\frac{1}{4}+\frac{1}{5}+\frac{1}{6}−\frac{1}{7}−\frac{1}{8}+⋯\)

49)\(\displaystyle 1+\frac{1}{2}−\frac{1}{3}+\frac{1}{4}+\frac{1}{5}−\frac{1}{6}+\frac{1}{7}+\frac{1}{8}−\frac{1}{9}+⋯\)

Contestar

No alternando. Se puede expresar como\(\displaystyle \sum_{n=1}^∞\left(\frac{1}{3n−2}+\frac{1}{3n−1}−\frac{1}{3n}\right),\) que diverge en comparación con\(\displaystyle \sum_{n=1}^∞\frac{1}{3n−2}.\)

50) Demostrar que la serie alterna\(\displaystyle 1−\frac{1}{2}+\frac{1}{2}−\frac{1}{4}+\frac{1}{3}−\frac{1}{6}+\frac{1}{4}−\frac{1}{8}+⋯\) no converge. ¿Qué hipótesis de la prueba de series alternas no se cumple?

51) Supongamos que\(\displaystyle \sum a_n\) converge absolutamente. Mostrar que la serie que consiste en los términos positivos\(a_n\) también converge.

Contestar

Que\(a^+_n=a_n\) si\(a_n≥0\) y\(a^+_n=0\) si\( a_n<0\). Entonces\(a^+_n≤|a_n|\) para todos\(n\) así la secuencia de sumas parciales de\( a^+_n\) está aumentando y delimitada arriba por la secuencia de sumas parciales de\( |a_n|\), que converge; de ahí,\(\displaystyle \sum_{n=1}^∞a^+_n\) converge.

52) Mostrar que la serie alterna\(\displaystyle \frac{2}{3}−\frac{3}{5}+\frac{4}{7}−\frac{5}{9}+⋯\) no converge. ¿Qué hipótesis de la prueba de series alternas no se cumple?

53) La fórmula\(\displaystyle \cos θ=1−\frac{θ^2}{2!}+\frac{θ^4}{4!}−\frac{θ^6}{6!}+⋯\) se derivará en el próximo capítulo. Use el resto\(|R_N|≤b_{N+1}\) para encontrar un límite para el error en la estimación\(\cos θ\) por la quinta suma parcial\(1−θ^2/2!+θ^4/4!−θ^6/6!+θ^8/8!\) para\(θ=1, θ=π/6,\) y\(θ=π.\)

Contestar

Para\(N=5\) uno tiene\(∣R_N∣b_6=θ^{10}/10!\). Cuando\(θ=1, R_5≤1/10!≈2.75×10^{−7}\). Cuando\(θ=π/6,\)\(R_5≤(π/6)^{10}/10!≈4.26×10^{−10}\). Cuando\(θ=π, R_5≤π^{10}/10!=0.0258.\)

54) La fórmula\(\sin θ=θ−\dfrac{θ^3}{3!}+\dfrac{θ^5}{5!}−\dfrac{θ^7}{7!}+⋯\) se derivará en el próximo capítulo. Use el resto\(|R_N|≤b_{N+1}\) para encontrar un límite para el error en la estimación\(\sin θ\) por la quinta suma parcial\(θ−θ^3/3!+θ^5/5!−θ^7/7!+θ^9/9!\) para\(θ=1, θ=π/6,\) y\(θ=π.\)

55) ¿Cuántos términos en\(\cos θ=1−\dfrac{θ^2}{2!}+\dfrac{θ^4}{4!}−\dfrac{θ^6}{6!}+⋯\) son necesarios para aproximarse\(\cos 1\) exacto a un error de como máximo\( 0.00001\)?

Contestar

\( b_n=1/(2n−2)!.\)Entonces,\(R_N≤1/(2N)!<0.00001\) cuando\((2N)!>10^5\) o\(N=5\) y\(\displaystyle 1−\frac{1}{2!}+\frac{1}{4!}−\frac{1}{6!}+\frac{1}{8!}=0.540325…\), mientras que\(\cos 1=0.5403023…\)

56) Cuántos términos en\(\sin θ=θ−\dfrac{θ^3}{3!}+\dfrac{θ^5}{5!}−\dfrac{θ^7}{7!}+⋯\) son necesarios para aproximarse\(\sin 1\) exacto a un error de como máximo\(0.00001?\)

57) A veces las series alternas\(\displaystyle \sum_{n=1}^∞(−1)^{n−1}b_n\) convergen a una cierta fracción de una serie absolutamente convergente\(\displaystyle \sum_{n=1}^∞b_n\) a un ritmo más rápido. Dado eso\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}=\frac{π^2}{6}\), encuentra\(\displaystyle S=1−\frac{1}{2^2}+\frac{1}{3^2}−\frac{1}{4^2}+⋯\). ¿Cuál de las series\(\displaystyle 6\sum_{n=1}^∞\frac{1}{n^2}\) y\(\displaystyle S\sum_{n=1}^∞\frac{(−1)^{n−1}}{n^2}\) da una mejor estimación del\(π^2\) uso de\(1000\) términos?

Contestar

Vamos\(\displaystyle T=\sum\frac{1}{n^2}.\) Entonces\(T−S=\dfrac{1}{2}T\), así\(S=T/2\). \(\displaystyle \sqrt{6×\sum_{n=1}^{1000}1/n^2}=3.140638…; \sqrt{\frac{1}{2}×\sum_{n=1}^{1000}(−1)^{n−1}/n^2}=3.141591…; π=3.141592….\)La serie alterna es más precisa para\(1000\) los términos.

Las series alternas en los ejercicios 58 & 59 convergen a múltiplos dados de\(π\). Encuentra el valor de\(N\) predicho por la estimación del resto de tal manera que la suma\(N^{\text{th}}\) parcial de la serie se aproxime con precisión al lado izquierdo hasta dentro del error dado. Encuentra el mínimo\(N\) para el que se mantiene el límite de error, y da el valor aproximado deseado en cada caso. Hasta\(15\) decimales,\( π=3.141592653589793….\)

58) [T]\(\displaystyle \frac{π}{4}=\sum_{n=0}^∞\frac{(−1)^n}{2n+1},\) error\(<0.0001\)

59) [T]\(\displaystyle \frac{π}{\sqrt{12}}=\sum_{k=0}^∞\frac{(−3)^{−k}}{2k+1},\) error\(<0.0001\)

Contestar

\(N=6, S_N=0.9068\)

60) [T] La serie\(\displaystyle \sum_{n=0}^∞\frac{\sin(x+πn)}{x+πn}\) juega un papel importante en el procesamiento de señales. Demostrar que\(\displaystyle \sum_{n=0}^∞\frac{\sin(x+πn)}{x+πn}\) converge cuando sea\(0<x<π\). (Pista: Usa la fórmula para el seno de una suma de ángulos.)

61) [T] Si\(\displaystyle \sum_{n=1}^N(−1)^{n−1}\frac{1}{n}→ln2,\) lo que es\(\displaystyle 1+\frac{1}{3}+\frac{1}{5}−\frac{1}{2}−\frac{1}{4}−\frac{1}{6}+\frac{1}{7}+\frac{1}{9}+\frac{1}{11}−\frac{1}{8}−\frac{1}{10}−\frac{1}{12}+⋯?\)

Contestar

\(\ln(2).\)La suma\(n^{\text{th}}\) parcial es la misma que para la serie armónica alterna.

62) [T] Trazar la serie\(\displaystyle \sum_{n=1}^{100}\frac{\cos(2πnx)}{n}\) para\(0≤x<1\). Explique por qué\(\displaystyle \sum_{n=1}^{100}\frac{\cos(2πnx)}{n}\) diverge cuando\(x=0,1\). ¿Cómo se comporta la serie para otros\(x\)?

63) [T] Trazar\(\displaystyle \sum_{n=1}^{100}\frac{\sin(2πnx)}{n}\) la serie\(0≤x<1\) y comentar su comportamiento

Contestar

La serie salta rápidamente cerca de los puntos finales. Para\(x\) lejos de los puntos finales, la gráfica se ve como\( π(1/2−x)\).

64) [T] Trazar la serie\(\displaystyle \sum_{n=1}^{100}\frac{\cos(2πnx)}{n^2}\)\( 0≤x<1\) y describir su gráfica.

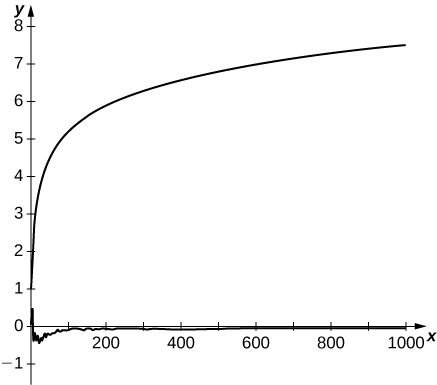
65) [T] La serie armónica alterna converge por cancelación entre sus términos. Su suma es conocida porque la cancelación puede describirse explícitamente. Una serie armónica aleatoria es una de la forma\(\displaystyle \sum_{n=1}^∞\frac{S_n}{n}\), donde\(s_n\) es una secuencia generada aleatoriamente\(±1's\) en la que los valores\(±1\) son igualmente probables de ocurrir. Usa un generador de números aleatorios para producir\(1000\) aleatorios\(±1's\) y trazar las sumas parciales\(\displaystyle S_N=\sum_{n=1}^N\frac{s_n}{n}\) de tu secuencia armónica aleatoria para\(N=1\) to\(1000\). Comparar con una gráfica de las primeras sumas\(1000\) parciales de la serie armónica.

Contestar

Aquí hay un resultado típico. La curva superior consiste en sumas parciales de la serie armónica. La curva inferior traza sumas parciales de una serie armónica aleatoria.

66) [T] Las estimaciones de\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\) pueden acelerarse escribiendo sus sumas parciales como\(\displaystyle \sum_{n=1}^N\frac{1}{n^2}=\sum_{n=1}^N\frac{1}{n(n+1)}+\sum_{n=1}^N\frac{1}{n^2(n+1)}\) y recordando que\(\displaystyle \sum_{n=1}^N\frac{1}{n(n+1)}=1−\frac{1}{N+1}\) converge a uno como\( N→∞.\) Comparar la estimación de\(π^2/6\) usar las sumas\(\displaystyle \sum_{n=1}^{1000}\frac{1}{n^2}\) con la estimación usando\(\displaystyle 1+\sum_{n=1}^{1000}\frac{1}{n^2(n+1)}\).

67) [T] La transformación de Euler reescribe\(\displaystyle S=\sum_{n=0}^∞(−1)^nb_n\) como\(\displaystyle S=\sum_{n=0}^∞(−1)^n2^{−n−1}\sum_{m=0}^n(^n_m)b_{n−m}\). Para la serie armónica alterna, toma la forma\(\displaystyle \ln(2)=\sum_{n=1}^∞\frac{(−1)^{n−1}}{n}=\sum_{n=1}^∞\frac{1}{n2^n}\). Calcular sumas parciales de\(\displaystyle \sum_{n=1}^∞\frac{1}{n2^n}\) hasta que se aproximen con\(\ln(2)\) precisión a dentro\(0.0001\). ¿Cuántos términos se necesitan? Comparar esta respuesta con el número de términos de las series armónicas alternas que se necesitan para estimar\(\ln(2)\).

Contestar

Por la prueba de series alternas,\(|S_n−S|≤b_{n+1},\) entonces uno necesita\(10^4\) términos de la serie armónica alterna\(\ln(2)\) para estimar dentro\(0.0001\). Las primeras sumas\(10\) parciales de la serie\(\displaystyle \sum_{n=1}^∞\frac{1}{n2^n}\) son (hasta cuatro decimales)\( 0.5000,0.6250,0.6667,0.6823,0.6885,0.6911,0.6923,0.6928,0.6930,0.6931\) y la décima suma parcial está dentro\(0.0001\) de\(\ln(2)=0.6931….\)

68) [T] En el texto se afirmó que una serie condicionalmente convergente puede ser reordenada para converger a cualquier número. Aquí hay un hecho un poco más simple, pero similar. Si\(a_n≥0\) es tal que\(a_n→0\) como\(n→∞\) pero\(\displaystyle \sum_{n=1}^∞a_n\) diverge, entonces, dado cualquier número\(A\) hay una secuencia\(s_n\) de\( ±1's\) tal que\(\displaystyle \sum_{n=1}^∞a_ns_n→A.\) Mostrar esto para\(A>0\) lo siguiente.

a. definir recursivamente\(s_n\) por\( s_n=1\) si\(\displaystyle S_{n−1}=\sum_{k=1}^{n−1}a_ks_k<A\) y de\( s_n=−1\) otra manera.

b. explicar por qué eventualmente\(S_n≥A,\) y para cualquier\(m\) mayor que esto\(n\),\(A−a_m≤S_m≤A+a_m\).

c. Explique por qué esto implica que\( S_n→A\) como\( n→∞.\)