10.1E: Ejercicios para la Sección 10.1

Última actualización
Guardar como PDF

Page ID: 116125

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En los ejercicios 1 - 4, indique si cada enunciado es verdadero, o dar un ejemplo para demostrar que es falsa.

1) Si$\displaystyle \sum_{n=1}^∞a_nx^n$ converge, entonces$a_nx^n→0$ como$n→∞.$

Responder: Cierto. Si una serie converge entonces sus términos tienden a cero.

2)$\displaystyle \sum_{n=1}^∞a_nx^n$ converge en$x=0$ para cualquier número real$a_n$.

3) Dada cualquier secuencia$a_n$, siempre hay alguna$R>0$, posiblemente muy pequeña, tal que$\displaystyle \sum_{n=1}^∞a_nx^n$ converge en$(−R,R)$.

Responder: Falso. Eso implicaría que$a_nx^n→0$ para$|x|<R$. Si$a_n=n^n$, entonces$a_nx^n=(nx)^n$ no tiende a cero para ninguno$x≠0$.

4) Si$\displaystyle \sum_{n=1}^∞a_nx^n$ tiene radio de convergencia$R>0$ y si$|b_n|≤|a_n|$ para todos$n$, entonces el radio de convergencia de$\displaystyle \sum_{n=1}^∞b_nx^n$ es mayor o igual a$R$.

5) Supongamos que$\displaystyle \sum_{n=0}^∞a_n(x−3)^n$ converge en$x=6$. ¿En cuál de los siguientes puntos debe converger también la serie? Usa el hecho de que si$\displaystyle \sum a_n(x−c)^n$ converge en$x$, entonces converge en cualquier punto más cercano a$c$ que$x$.

a.$x=1$

b.$x=2$

c.$x=3$

d.$x=0$

e.$x=5.99$

f.$x=0.000001$

Responder: Debe converger sobre$(0,6]$ y por lo tanto en: a.$x=1$; b.$x=3$; c.; d.$x=0$; e.$x=5.99$; y f$x=0.000001$.$x=2$

6) Supongamos que$\displaystyle \sum_{n=0}^∞a_n(x+1)^n$ converge en$x=−2$. ¿En cuál de los siguientes puntos debe converger también la serie? Usa el hecho de que si$\displaystyle \sum a_n(x−c)^n$ converge en$x$, entonces converge en cualquier punto más cercano a$c$ que$x$.

a.$x=2$

b.$x=−1$

c.$x=−3$

d.$x=0$

e.$x=0.99$

f.$x=0.000001$

En los siguientes ejercicios, supongamos que$\left|\dfrac{a_{n+1}}{a_n}\right|→1$ como$n→∞.$ Encuentra el radio de convergencia para cada serie.

7)$\displaystyle \sum_{n=0}^∞a_n2^nx^n$

Responder: $\left|\dfrac{a_{n+1}2^{n+1}x^{n+1}}{a_n2^nx^n}\right| =2|x|\left|\dfrac{a_{n+1}}{a_n}\right|→2|x|$entonces$R=\frac{1}{2}$

8)$\displaystyle \sum_{n=0}^∞\frac{a_nx^n}{2^n}$

9)$\displaystyle \sum_{n=0}^∞\frac{a_nπ^nx^n}{e^n}$

Responder: $\left|\dfrac{a_{n+1}(\dfrac{π}{e})^{n+1}x^{n+1}}{a_n(\dfrac{π}{e})^nx^n}\right| =\dfrac{π|x|}{e}\left|\dfrac{a_{n+1}}{a_n}\right|→\dfrac{π|x|}{e}$entonces$R=\frac{e}{π}$

10)$\displaystyle \sum_{n=0}^∞\frac{a_n(−1)^nx^n}{10^n}$

11)$\displaystyle \sum_{n=0}^∞a_n(−1)^nx^{2n}$

Responder: $\left|\dfrac{a_{n+1}(−1)^{n+1}x^{2n+2}}{a_n(−1)^nx^{2n}}\right| =|x^2|\left|\dfrac{a_{n+1}}{a_n}\right|→|x^2|$entonces$R=1$

12)$\displaystyle \sum_{n=0}^∞a_n(−4)^nx^{2n}$

En los ejercicios 13 - 22, encuentra el radio de convergencia$R$ y el intervalo de convergencia para$\displaystyle \sum a_nx^n$ con los coeficientes dados$a_n$.

13)$\displaystyle \sum_{n=1}^∞\frac{(2x)^n}{n}$

Responder: $a_n=\dfrac{2^n}{n}$así$\dfrac{a_{n+1}x}{a_n}→2x$. entonces$R=\frac{1}{2}$. Cuando$x=\frac{1}{2}$ la serie es armónica y diverge. Cuando$x=−\frac{1}{2}$ la serie es armónica alterna y converge. El intervalo de convergencia es$I=\big[−\frac{1}{2},\frac{1}{2}\big)$.

14)$\displaystyle \sum_{n=1}^∞(−1)^n\frac{x^n}{\sqrt{n}}$

15)$\displaystyle \sum_{n=1}^∞\frac{nx^n}{2^n}$

Responder: $a_n=\dfrac{n}{2^n}$así$\dfrac{a_{n+1}x}{a_n}→\dfrac{x}{2}$ que así$R=2$. Cuando$x=±2$ la serie diverge por la prueba de divergencia. El intervalo de convergencia es$I=(−2,2)$.

16)$\displaystyle \sum_{n=1}^∞\frac{nx^n}{e^n}$

17)$\displaystyle \sum_{n=1}^∞\frac{n^2x^n}{2^n}$

Responder: $a_n=\dfrac{n^2}{2^n}$así$R=2$. Cuando$x=±2$ la serie diverge por la prueba de divergencia. El intervalo de convergencia es$I=(−2,2).$

18)$\displaystyle \sum_{k=1}^∞\frac{k^ex^k}{e^k}$

19)$\displaystyle \sum_{k=1}^∞\frac{π^kx^k}{k^π}$

Responder: $a_k=\dfrac{π^k}{k^π}$así$R=\frac{1}{π}$. Cuando$x=±\frac{1}{π}$ la serie es una$p$ serie absolutamente convergente. El intervalo de convergencia es$I=\left[−\frac{1}{π},\frac{1}{π}\right].$

20)$\displaystyle \sum_{n=1}^∞\frac{x^n}{n!}$

21)$\displaystyle \sum_{n=1}^∞\frac{10^nx^n}{n!}$

Responder: $a_n=\dfrac{10^n}{n!},\dfrac{a_{n+1}x}{a_n}=\dfrac{10x}{n+1}→0<1$por lo que la serie converge para todos$x$ por la prueba de ratio y$I=(−∞,∞)$.

22)$\displaystyle \sum_{n=1}^∞(−1)^n\frac{x^n}{\ln(2n)}$

En los ejercicios 23 - 28, encuentra el radio de convergencia de cada serie.

23)$\displaystyle \sum_{k=1}^∞\frac{(k!)^2x^k}{(2k)!}$

Responder: $a_k=\dfrac{(k!)^2}{(2k)!}$tan$\dfrac{a_{k+1}}{a_k}=\dfrac{(k+1)^2}{(2k+2)(2k+1)}→\dfrac{1}{4}$ tan$R=4$

24)$\displaystyle \sum_{n=1}^∞\frac{(2n)!x^n}{n^{2n}}$

25)$\displaystyle \sum_{k=1}^∞\frac{k!}{1⋅3⋅5⋯(2k−1)}x^k$

Responder: $a_k=\dfrac{k!}{1⋅3⋅5⋯(2k−1)}$tan$\dfrac{a_{k+1}}{a_k}=\dfrac{k+1}{2k+1}→\dfrac{1}{2}$ tan$R=2$

26)$\displaystyle \sum_{k=1}^∞\frac{2⋅4⋅6⋯2k}{(2k)!}x^k$

27)$\displaystyle \sum_{n=1}^∞\frac{x^n}{(^{2n}_n)}$ donde$(^n_k)=\dfrac{n!}{k!(n−k)!}$

Responder: $a_n=\dfrac{1}{(^{2n}_n)}$tan$\dfrac{a_{n+1}}{a_n}=\dfrac{\big((n+1)!\big)^2}{(2n+2)!}\dfrac{2n!}{(n!)^2}=\dfrac{(n+1)^2}{(2n+2)(2n+1)}→\dfrac{1}{4}$ tan$R=4$

28)$\displaystyle \sum_{n=1}^∞\sin^2nx^n$

En los ejercicios 29 - 32, utilice la prueba de ratio para determinar el radio de convergencia de cada serie.

29)$\displaystyle \sum_{n=1}^∞\frac{(n!)^3}{(3n)!}x^n$

Responder: $\dfrac{a_{n+1}}{a_n}=\dfrac{(n+1)^3}{(3n+3)(3n+2)(3n+1)}→\dfrac{1}{27}$entonces$R=27$

30)$\displaystyle \sum_{n=1}^∞\frac{2^{3n}(n!)^3}{(3n)!}x^n$

31)$\displaystyle \sum_{n=1}^∞\frac{n!}{n^n}x^n$

Responder: $a_n=\dfrac{n!}{n^n}$tan$\dfrac{a_{n+1}}{a_n}=\dfrac{(n+1)!}{n!}\dfrac{n^n}{(n+1)^{n+1}}=(\dfrac{n}{n+1})^n→\dfrac{1}{e}$ tan$R=e$

32)$\displaystyle \sum_{n=1}^∞\frac{(2n)!}{n^{2n}}x^n$

En los siguientes ejercicios, dado que$\displaystyle \frac{1}{1−x}=\sum_{n=0}^∞x^n$ con convergencia en$(−1,1)$, encontrar la serie de potencia para cada función con el centro dado$a,$ e identificar su intervalo de convergencia.

33)$f(x)=\dfrac{1}{x};a=1$ (Pista:$\dfrac{1}{x}=\dfrac{1}{1−(1−x)})$

Responder: $\displaystyle f(x)=\sum_{n=0}^∞(1−x)^n$en$I=(0,2)$

34)$f(x)=\dfrac{1}{1−x^2};a=0$

35)$f(x)=\dfrac{x}{1−x^2};a=0$

Responder: $\displaystyle \sum_{n=0}^∞x^{2n+1}$en$I=(−1,1)$

36)$f(x)=\dfrac{1}{1+x^2};a=0$

37)$f(x)=\dfrac{x^2}{1+x^2};a=0$

Responder: $\displaystyle \sum_{n=0}^∞(−1)^nx^{2n+2}$en$I=(−1,1)$

38)$f(x)=\dfrac{1}{2−x};a=1$

39)$f(x)=\dfrac{1}{1−2x};a=0.$

Responder: $\displaystyle \sum_{n=0}^∞2^nx^n$en$\left(−\frac{1}{2},\frac{1}{2}\right)$

40)$f(x)=\dfrac{1}{1−4x^2};a=0$

41)$f(x)=\dfrac{x^2}{1−4x^2};a=0$

Responder: $\displaystyle \sum_{n=0}^∞4^nx^{2n+2}$en$\left(−\frac{1}{2},\frac{1}{2}\right)$

42)$f(x)=\dfrac{x^2}{5−4x+x^2};a=2$

Utilizar el resultado del ejercicio 43 para encontrar el radio de convergencia de la serie dada en los ejercicios posteriores (44 - 47).

43) Explicar por qué, si$|a_n|^{1/n}→r>0,$ entonces$|a_nx^n|^{1/n}→|x|r<1$ cuando$|x|<\frac{1}{r}$ y, por lo tanto, el radio de convergencia de$\displaystyle \sum_{n=1}^∞a_nx^n$ es$R=\frac{1}{r}$.

Responder: $|a_nx^n|^{1/n}=|a_n|^{1/n}|x|→|x|r$como$n→∞$ y$|x|r<1$ cuando$|x|<\frac{1}{r}$. Por lo tanto,$\displaystyle \sum_{n=1}^∞a_nx^n$ converge cuando$|x|<\frac{1}{r}$ por la prueba$n^{\text{th}}$ raíz.

44)$\displaystyle \sum_{n=1}^∞\frac{x^n}{n^n}$

45)$\displaystyle \sum_{k=1}^∞\left(\frac{k−1}{2k+3}\right)^kx^k$

Responder: $a_k=\left(\dfrac{k−1}{2k+3}\right)^k$tan$(a_k)^{1/k}→\frac{1}{2}<1$ tan$R=2$

46)$\displaystyle \sum_{k=1}^∞(\frac{2k^2−1}{k^2+3})^kx^k$

47)$\displaystyle \sum_{n=1}^∞a_n=(n^{1/n}−1)^nx^n$

Responder: $a_n=(n^{1/n}−1)^n$tan$(a_n)^{1/n}→0$ tan$R=∞$

48) Supongamos que$\displaystyle p(x)=\sum_{n=0}^∞a_nx^n$ tal que$a_n=0$ si$n$ es par. Explicar por qué$p(x)=p(−x).$

49) Supongamos que$\displaystyle p(x)=\sum_{n=0}^∞a_nx^n$ tal que$a_n=0$ si$n$ es impar. Explicar por qué$p(x)=−p(−x).$

Responder: Podemos reescribir$\displaystyle p(x)=\sum_{n=0}^∞a_{2n+1}x^{2n+1}$ y$p(x)=p(−x)$ desde entonces$x^{2n+1}=−(−x)^{2n+1}$.

50) Supongamos que$\displaystyle p(x)=\sum_{n=0}^∞a_nx^n$ converge en$(−1,1]$. Encuentra el intervalo de convergencia de$p(Ax)$.

51) Supongamos que$\displaystyle p(x)=\sum_{n=0}^∞a_nx^n$ converge en$(−1,1]$. Encuentra el intervalo de convergencia de$p(2x−1)$.

Responder: Si$x∈[0,1],$ entonces$y=2x−1∈[−1,1]$ así$\displaystyle p(2x−1)=p(y)=\sum_{n=0}^∞a_ny^n$ converge.

En los siguientes ejercicios, supongamos que$\displaystyle p(x)=\sum_{n=0}^∞a_nx^n$ satisface$\displaystyle \lim_{n→∞}\frac{a_{n+1}}{a_n}=1$ donde$a_n≥0$ para cada uno$n$. Declarar si cada serie converge en el intervalo completo$(−1,1)$, o si no hay suficiente información para sacar una conclusión. Utilice la prueba de comparación cuando sea apropiado.

52)$\displaystyle \sum_{n=0}^∞a_nx^{2n}$

53)$\displaystyle \sum_{n=0}^∞a_{2n}x^{2n}$

Responder: Converge$(−1,1)$ por la prueba de ratio

54)$\displaystyle \sum_{n=0}^∞a_{2n}x^n$ (Pista:$x=±\sqrt{x^2}$)

55)$\displaystyle \sum_{n=0}^∞a_{n^2}x^{n^2}$ (Pista: Que$b_k=a_k$ si$k=n^2$ para algunos$n$, de lo contrario$b_k=0$.)

Responder: Considera la serie$\displaystyle \sum b_kx^k$ donde$b_k=a_k$ si$k=n^2$ y de$b_k=0$ otra manera. Entonces$b_k≤a_k$ y así la serie converge$(−1,1)$ por la prueba de comparación.

56) Supongamos que$p(x)$ es un polinomio de grado$N$. Encuentra el radio e intervalo de convergencia de$\displaystyle \sum_{n=1}^∞p(n)x^n$.

57) [T] Trazar las gráficas de$\dfrac{1}{1−x}$ y de las sumas parciales$\displaystyle S_N=\sum_{n=0}^Nx^n$ para$n=10,20,30$ en el intervalo$[−0.99,0.99]$. Comentar sobre la aproximación de$\dfrac{1}{1−x}$ por$S_N$ cerca$x=−1$ y cerca a$x=1$ medida que$N$ aumenta.

Responder

La aproximación es más precisa cerca$x=−1$. Las sumas parciales siguen$\dfrac{1}{1−x}$ más de cerca como$N$ aumentos pero nunca son acertadas$x=1$ ya que la serie diverge allí.

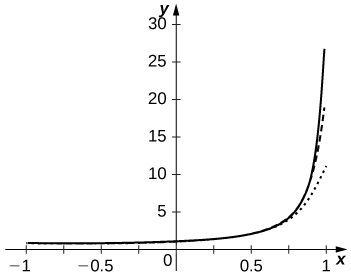
$Esta cifra es la gráfica de y = 1/ (1-x), que es una curva creciente con asíntota vertical a 1.$

58) [T] Trazar las gráficas de$−\ln(1−x)$ y de las sumas parciales$\displaystyle S_N=\sum_{n=1}^N\frac{x^n}{n}$ para$n=10,50,100$ en el intervalo$[−0.99,0.99]$. Comentar sobre el comportamiento de las sumas cercanas$x=−1$ y cercanas a$x=1$ medida que$N$ aumenta.

59) [T] Trazar las gráficas de las sumas parciales$\displaystyle S_n=\sum_{n=1}^N\frac{x^n}{n^2}$ para$n=10,50,100$ en el intervalo$[−0.99,0.99]$. Comentar sobre el comportamiento de las sumas cercanas$x=−1$ y cercanas a$x=1$ medida que$N$ aumenta.

Responder

La aproximación parece estabilizarse rápidamente cerca de ambos$x=±1$.

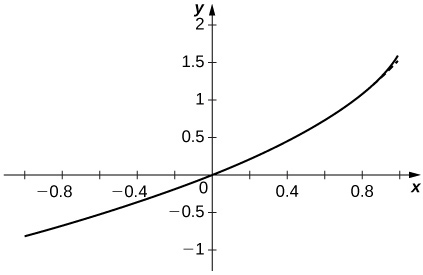
$Esta cifra es la gráfica de y = -ln (1-x) que es una curva creciente que pasa por el origen.$

60) [T] Trazar las gráficas de las sumas parciales$\displaystyle S_N=\sum_{n=1}^N(\sin n) x^n$ para$n=10,50,100$ en el intervalo$[−0.99,0.99]$. Comentar sobre el comportamiento de las sumas cercanas$x=−1$ y cercanas a$x=1$ medida que$N$ aumenta.

61) [T] Trazar las gráficas de las sumas parciales$\displaystyle S_N=\sum_{n=0}^N(−1)^n\frac{x^{2n+1}}{(2n+1)!}$ para$n=3,5,10$ en el intervalo$[−2π,2π]$. Comenta cómo estas parcelas se aproximan a$\sin x$ medida que$N$ aumenta.

Responder

Las curvas polinómicas tienen raíces cercanas a las de$\sin x$ hasta su grado y luego los polinomios divergen de$\sin x$.

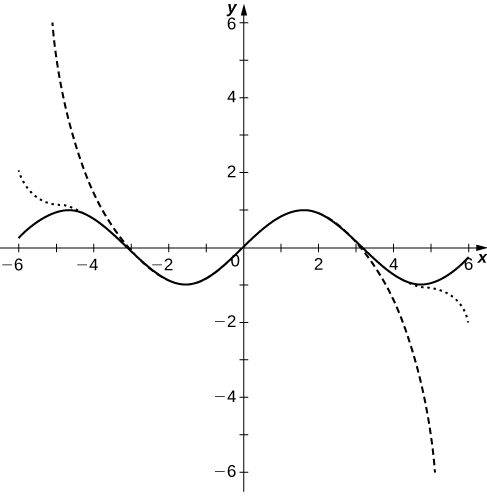
$Esta cifra es la gráfica de las sumas parciales de (-1) ^n veces x^ (2n+1) divididas por (2n+1)! Para n=3,5,10. Las curvas se aproximan a la curva sinusoidal cercana al origen y luego se separan a medida que las curvas se alejan del origen.$

62) [T] Trazar las gráficas de las sumas parciales$\displaystyle S_N=\sum_{n=0}^N(−1)^n\frac{x^{2n}}{(2n)!}$ para$n=3,5,10$ en el intervalo$[−2π,2π]$. Comenta cómo estas parcelas se aproximan a$\cos x$ medida que$N$ aumenta.

Colaboradores

Template:ContribOpenStaxCalc