10.2E: Ejercicios para la Sección 10.2

1) Si\(\displaystyle f(x)=\sum_{n=0}^∞\frac{x^n}{n!}\) y\(\displaystyle g(x)=\sum_{n=0}^∞(−1)^n\frac{x^n}{n!}\), encontrar la serie de poder de\(\frac{1}{2}\big(f(x)+g(x)\big)\) y de\(\frac{1}{2}\big(f(x)−g(x)\big)\).

Contestar

\(\displaystyle \frac{1}{2}\big(f(x)+g(x)\big)=\sum_{n=0}^∞\frac{x^{2n}}{(2n)!}\)y\(\displaystyle \frac{1}{2}\big(f(x)−g(x)\big)=\sum_{n=0}^∞\frac{x^{2n+1}}{(2n+1)!}\).

2) Si\(\displaystyle C(x)=\sum_{n=0}^∞\frac{x^{2n}}{(2n)!}\) y\(\displaystyle S(x)=\sum_{n=0}^∞\frac{x^{2n+1}}{(2n+1)!}\), encontrar la serie de poder de\(C(x)+S(x)\) y de\(C(x)−S(x)\).

En los ejercicios 3 - 6, usa fracciones parciales para encontrar la serie de potencia de cada función.

3)\(\dfrac{4}{(x−3)(x+1)}\)

Contestar

\(\displaystyle \frac{4}{(x−3)(x+1)}=\frac{1}{x−3}−\frac{1}{x+1}=−\frac{1}{3(1−\frac{x}{3})}−\frac{1}{1−(−x)}=−\frac{1}{3}\sum_{n=0}^∞\left(\frac{x}{3}\right)^n−\sum_{n=0}^∞(−1)^nx^n=\sum_{n=0}^∞\left((−1)^{n+1}−\frac{1}{3n+1}\right)x^n\)

4)\(\dfrac{3}{(x+2)(x−1)}\)

5)\(\dfrac{5}{(x^2+4)(x^2−1)}\)

Contestar

\(\displaystyle \frac{5}{(x^2+4)(x^2−1)}=\frac{1}{x^2−1}−\frac{1}{4}\frac{1}{1+\left(\frac{x}{2}\right)^2}=−\sum_{n=0}^∞x^{2n}−\frac{1}{4}\sum_{n=0}^∞(−1)^n\left(\frac{x}{2}\right)^n=\sum_{n=0}^∞\left((−1)+(−1)^{n+1}\frac{1}{2^{n+2}}\right)x^{2n}\)

6)\(\dfrac{30}{(x^2+1)(x^2−9)}\)

En los ejercicios 7 - 10, expresar cada serie como una función racional.

7)\(\displaystyle \sum_{n=1}^∞\frac{1}{x^n}\)

Contestar

\(\displaystyle \frac{1}{x}\sum_{n=0}^∞\frac{1}{x^n}=\frac{1}{x}\cdot \frac{1}{1−\frac{1}{x}}=\frac{1}{x−1}\)

8)\(\displaystyle \sum_{n=1}^∞\frac{1}{x^{2n}}\)

9)\(\displaystyle \sum_{n=1}^∞\frac{1}{(x−3)^{2n−1}}\)

Contestar

\(\displaystyle \frac{1}{x−3}\cdot \frac{1}{1−\frac{1}{(x−3)^2}}=\frac{x−3}{(x−3)^2−1}\)

10)\(\displaystyle \sum_{n=1}^∞\left(\frac{1}{(x−3)^{2n−1}}−\frac{1}{(x−2)^{2n−1}}\right)\)

Los ejercicios 11 - 16 exploran las aplicaciones de anualidades.

11) Calcular los valores actuales\(P\) de una anualidad en la que se pagarán anualmente $10,000 por un periodo de 20 años, asumiendo tasas de interés de\(r=0.03,\, r=0.05\), y\(r=0.07\).

Contestar

\(P=P_1+⋯+P_{20}\)donde\(P_k=10,000\dfrac{1}{(1+r)^k}\). Entonces\(\displaystyle P=10,000\sum_{k=1}^{20}\frac{1}{(1+r)^k}=10,000\frac{1−(1+r)^{−20}}{r}\). Cuando\(r=0.03, \,P≈10,000×14.8775=148,775.\) Cuando\(r=0.05, \,P≈10,000×12.4622=124,622.\) Cuando\(r=0.07, \, P≈105,940\).

12) Calcular los valores actuales\(P\) de anualidades en las cuales $9,000 se va a pagar anualmente perpetuamente, asumiendo tasas de interés de\(r=0.03,\, r=0.05\) y\(r=0.07\).

13) Calcular los pagos anuales\(C\) que se darán por 20 años sobre anualidades que tengan valor presente $100,000 asumiendo las tasas de interés respectivas de\(r=0.03,\, r=0.05,\) y\(r=0.07.\)

Contestar

En general,\(P=\dfrac{C(1−(1+r)^{−N})}{r}\) por\(N\) años de pagos, o\(C=\dfrac{Pr}{1−(1+r)^{−N}}\). Para\(N=20\) y\(P=100,000\), uno tiene\(C=6721.57\)\(r=0.03; \, C=8024.26\) cuando\(r=0.05\); y\(C≈9439.29\) cuando\(r=0.07\).

14) Calcular los pagos anuales\(C\) a dar perpetuamente sobre anualidades que tengan valor presente $100,000 asumiendo las respectivas tasas de interés de\(r=0.03, \,r=0.05,\) y\(r=0.07\).

15) Supongamos que una anualidad tiene un valor presente\(P=1\) millones de dólares. ¿Qué tasa de interés\(r\) permitiría pagos anuales perpetuos de $50,000?

Contestar

En general,\(P=\dfrac{C}{r}.\) Así,\(r=\dfrac{C}{P}=5×\frac{10^4}{10^6}=0.05.\)

16) Supongamos que una anualidad tiene un valor presente\(P=10\) millones de dólares. ¿Qué tasa de interés\(r\) permitiría pagos anuales perpetuos de $100,000?

En los ejercicios 17 - 20, expresar la suma de cada serie de poder en términos de series geométricas, y luego expresar la suma como una función racional.

17)\(x+x^2−x^3+x^4+x^5−x^6+⋯\) (Pista: Poderes de grupo\(x^{3k}, \, x^{3k−1},\) y\(x^{3k−2}\).)

Contestar

\((x+x^2−x^3)(1+x^3+x^6+⋯)=\dfrac{x+x^2−x^3}{1−x^3}\)

18)\(x+x^2−x^3−x^4+x^5+x^6−x^7−x^8+⋯\) (Pista: Poderes de grupo\(x^{4k}, \, x^{4k−1},\), etc.)

19)\(x−x^2−x^3+x^4−x^5−x^6+x^7−⋯\) (Pista: Poderes de grupo\(x^{3k}, \, x^{3k−1}\), y\(x^{3k−2}\).)

Contestar

\((x−x^2−x^3)(1+x^3+x^6+⋯)=\dfrac{x−x^2−x^3}{1−x^3}\)

20)\(\displaystyle \frac{x}{2}+\frac{x^2}{4}−\frac{x^3}{8}+\frac{x^4}{16}+\frac{x^5}{32}−\frac{x^6}{64}+⋯\) (Pista: Poderes de grupo\(\left(\dfrac{x}{2}\right)^{3k}, \, \left(\dfrac{x}{2}\right)^{3k−1},\) y\(\left(\dfrac{x}{2}\right)^{3k−2}\).)

En los ejercicios 21 - 24, encuentra la serie de poder de\(f(x)g(x)\) dado\(f\) y\(g\) como se define.

21)\(\displaystyle f(x)=2\sum_{n=0}^∞x^n,g(x)=\sum_{n=0}^∞nx^n\)

Contestar

\(a_n=2, \, b_n=n\)así\(\displaystyle c_n=\sum_{k=0}^nb_ka_{n−k}=2\sum_{k=0}^nk=(n)(n+1)\) y\(\displaystyle f(x)g(x)=\sum_{n=1}^∞n(n+1)x^n\)

22)\(\displaystyle f(x)=\sum_{n=1}^∞x^n,\; g(x)=\sum_{n=1}^∞\frac{1}{n}x^n\). Expresar los coeficientes de\(f(x)g(x)\) en términos de\(\displaystyle H_n=\sum_{k=1}^n\frac{1}{k}\).

23)\(\displaystyle f(x)=g(x)=\sum_{n=1}^∞\left(\frac{x}{2}\right)^n\)

Contestar

\(a_n=b_n=2^{−n}\)así\(\displaystyle c_n=\sum_{k=1}^nb_ka_{n−k}=2^{−n}\sum_{k=1}^n1=\frac{n}{2^n}\) y\(\displaystyle f(x)g(x)=\sum_{n=1}^∞n\left(\frac{x}{2}\right)^n\)

24)\(\displaystyle f(x)=g(x)=\sum_{n=1}^∞nx^n\)

En los ejercicios 25 - 26, diferenciar la expansión de serie dada de\(f\) término por término para obtener la expansión de serie correspondiente para la derivada de\(f.\)

25)\(\displaystyle f(x)=\frac{1}{1+x}=\sum_{n=0}^∞(−1)^nx^n\)

Contestar

El derivado de\(f\) es\(\displaystyle −\frac{1}{(1+x)^2}=−\sum_{n=0}^∞(−1)^n(n+1)x^n\).

26)\(\displaystyle f(x)=\frac{1}{1−x^2}=\sum_{n=0}^∞x^{2n}\)

En los ejercicios 27 - 28, integrar la expansión de serie dada\(f\) de término por término de cero\(x\) para obtener la expansión de serie correspondiente para la integral indefinida de\(f\).

27)\(\displaystyle f(x)=\frac{2x}{(1+x^2)^2}=\sum_{n=1}^∞(−1)^n(2n)x^{2n−1}\)

Contestar

La integral indefinida de\(f\) es\(\displaystyle \frac{1}{1+x^2}=\sum_{n=0}^∞(−1)^nx^{2n}\).

28)\(\displaystyle f(x)=\frac{2x}{1+x^2}=2\sum_{n=0}^∞(−1)^nx^{2n+1}\)

En los ejercicios 29 - 32, evaluar cada serie infinita identificándola como el valor de una derivada o integral de series geométricas.

29) Evaluar\(\displaystyle \sum_{n=1}^∞\frac{n}{2^n}\) como\(f′\left(\frac{1}{2}\right)\) dónde\(\displaystyle f(x)=\sum_{n=0}^∞x^n\).

Contestar

\(\displaystyle f(x)=\sum_{n=0}^∞x^n=\frac{1}{1−x}; \; f′(\frac{1}{2})=\sum_{n=1}^∞\frac{n}{2^{n−1}}=\frac{d}{dx}(1−x)^{−1}\Big|_{x=1/2}=\frac{1}{(1−x)^2}\Big|_{x=1/2}=4\)por lo\(\displaystyle \sum_{n=1}^∞\frac{n}{2^n}=2.\)

30) Evaluar\(\displaystyle \sum_{n=1}^∞\frac{n}{3^n}\) como\(f′\left(\frac{1}{3}\right)\) dónde\(\displaystyle f(x)=\sum_{n=0}^∞x^{6n}\).

31) Evaluar\(\displaystyle \sum_{n=2}^∞\frac{n(n−1)}{2^n}\) como\(f''\left(\frac{1}{2}\right)\) dónde\(\displaystyle f(x)=\sum_{n=0}^∞x^n\).

Contestar

\(\displaystyle f(x)=\sum_{n=0}^∞x^n=\frac{1}{1−x}; \; f''\left(\frac{1}{2}\right)=\sum_{n=2}^∞\frac{n(n−1)}{2^{n−2}}=\frac{d^2}{dx^2}(1−x)^{−1}\Big|_{x=1/2}=\frac{2}{(1−x)^3}\Big|_{x=1/2}=16\)por lo\(\displaystyle \sum_{n=2}^∞n\frac{(n−1)}{2^n}=4.\)

32) Evaluar\(\displaystyle \sum_{n=0}^∞\frac{(−1)^n}{n+1}\) como\(\displaystyle ∫^1_0f(t) \, dt\) dónde\(\displaystyle f(x)=\sum_{n=0}^∞(−1)^nx^{2n}=\frac{1}{1+x^2}\).

En los ejercicios 33 - 39, dado que\(\displaystyle \frac{1}{1−x}=\sum_{n=0}^∞x^n\), utilizar la diferenciación o integración término por término para encontrar series de potencia para cada función centrada en el punto dado.

33)\(f(x)=\ln x\) centrado en\(x=1\) (Pista:\(x=1−(1−x)\))

Contestar

\(\displaystyle ∫\sum(1−x)^n\,dx=∫\sum(−1)^n(x−1)^n\,dx=\sum \frac{(−1)^n(x−1)^{n+1}}{n+1}\)

34)\(\ln(1−x)\) en\(x=0\)

35)\(\ln(1−x^2)\) en\(x=0\)

Contestar

\(\displaystyle −∫^{x^2}_{t=0}\frac{1}{1−t}dt=−\sum_{n=0}^∞∫^{x^2}_0t^ndx−\sum_{n=0}^∞\frac{x^{2(n+1)}}{n+1}=−\sum_{n=1}^∞\frac{x^{2n}}{n}\)

36)\(f(x)=\dfrac{2x}{(1−x^2)^2}\) en\(x=0\)

37)\(f(x)=\tan^{−1}(x^2)\) en\(x=0\)

Contestar

\(\displaystyle ∫^{x^2}_0\frac{dt}{1+t^2}=\sum_{n=0}^∞(−1)^n∫^{x^2}_0t^{2n}dt=\sum_{n=0}^∞(−1)^n\frac{t^{2n+1}}{2n+1}∣^{x^2}_{t=0}=\sum_{n=0}^∞(−1)^n\frac{x^{4n+2}}{2n+1}\)

38)\(f(x)=\ln(1+x^2)\) en\(x=0\)

39)\(\displaystyle f(x)=∫^x_0\ln t\,dt\) donde\(\displaystyle \ln(x)=\sum_{n=1}^∞(−1)^{n−1}\frac{(x−1)^n}{n}\)

Contestar

La integración término por término da\(\displaystyle ∫^x_0\ln t\,dt=\sum_{n=1}^∞(−1)^{n−1}\frac{(x−1)^{n+1}}{n(n+1)}=\sum_{n=1}^∞(−1)^{n−1}\left(\frac{1}{n}−\frac{1}{n+1}\right)(x−1)^{n+1}=(x−1)\ln x+\sum_{n=2}^∞(−1)^n\frac{(x−1)^n}{n}=x\ln x−x.\)

40) [T] Evaluar la expansión de la serie de potencia\(\displaystyle \ln(1+x)=\sum_{n=1}^∞(−1)^{n−1}\frac{x^n}{n}\) en\(x=1\) para mostrar que\(\ln(2)\) es la suma de la serie armónica alterna. Utilice la prueba de series alternas para determinar cuántos términos de la suma se necesitan para estimar con\(\ln(2)\) precisión dentro\(0.001,\) y encontrar tal aproximación.

41) [T] Restar la serie infinita de\(\ln(1−x)\) de\(\ln(1+x)\) para obtener una serie de potencia para\(\ln\left(\dfrac{1+x}{1−x}\right)\). Evaluar en\(x=\frac{1}{3}\). ¿Cuál es el menor de\(N\) tal manera que la suma\(N^{\text{th}}\) parcial de esta serie se aproxima\(\ln(2)\) con un error menor que\(0.001\)?

Contestar

\(\displaystyle \ln(1−x)=−\sum_{n=1}^∞\frac{x^n}{n}\)Así lo tenemos\(\displaystyle \ln(1+x)=\sum_{n=1}^∞(−1)^{n−1}\frac{x^n}{n}\). Así,\(\displaystyle \ln\left(\frac{1+x}{1−x}\right)=\sum_{n=1}^∞\big(1+(−1)^{n−1}\big)\frac{x^n}{n}=2\sum_{n=1}^∞\frac{x^{2n−1}}{2n−1}\). Cuando\(x=\frac{1}{3}\) obtengamos\(\displaystyle \ln(2)=2\sum_{n=1}^∞\frac{1}{3^{2n−1}(2n−1)}\). Tenemos\(\displaystyle 2\sum_{n=1}^3\frac{1}{3^{2n−1}(2n−1)}=0.69300…\), mientras\(\displaystyle 2\sum_{n=1}^4\frac{1}{3^{2n−1}(2n−1)}=0.69313…\) y\(\ln(2)=0.69314…;\) por lo tanto,\(N=4\).

En los ejercicios 42 - 45, utilizando una sustitución si se indica, expresar cada serie en términos de funciones elementales y encontrar el radio de convergencia de la suma.

42)\(\displaystyle \sum_{k=0}^∞(x^k−x^{2k+1})\)

43)\(\displaystyle \sum_{k=1}^∞\frac{x^{3k}}{6k}\)

Contestar

\(\displaystyle \sum_{k=1}^∞\frac{x^k}{k}=−\ln(1−x)\)así\(\displaystyle \sum_{k=1}^∞\frac{x^{3k}}{6k}=−\frac{1}{6}\ln(1−x^3)\). El radio de convergencia es igual a\(1\) por la prueba de relación.

44)\(\displaystyle \sum_{k=1}^∞(1+x^2)^{−k}\) usando\(y=\dfrac{1}{1+x^2}\)

45)\(\displaystyle \sum_{k=1}^∞2^{−kx}\) usando\(y=2^{−x}\)

Contestar

Si\(y=2^{−x}\), entonces\(\displaystyle \sum_{k=1}^∞y^k=\frac{y}{1−y}=\frac{2^{−x}}{1−2^{−x}}=\frac{1}{2^x−1}\). Si\(a_k=2^{−kx}\), entonces\(\dfrac{a_{k+1}}{a_k}=2^{−x}<1\) cuando\(x>0\). Entonces la serie converge para todos\(x>0\).

46) Demostrar eso, hasta poderes\(x^3\) y\(y^3\),\(\displaystyle E(x)=\sum_{n=0}^∞\frac{x^n}{n!}\) satisface\(E(x+y)=E(x)E(y)\).

47) Diferenciar la\(\displaystyle E(x)=\sum_{n=0}^∞\frac{x^n}{n!}\) serie término por término para mostrar que\(E(x)\) es igual a su derivada.

Contestar

Las respuestas variarán.

48) Demostrar que si\(\displaystyle f(x)=\sum_{n=0}^∞a_nx^n\) es una suma de potencias pares, es decir,\(a_n=0\) si\(n\) es impar, entonces\(\displaystyle F=∫^x_0f(t)\, dt\) es una suma de potencias impares, mientras que si\(I\) es una suma de potencias impares, entonces\(F\) es una suma de potencias pares.

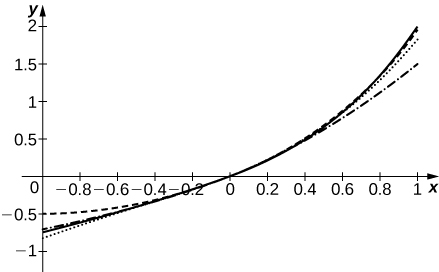
49) [T] Supongamos que los coeficientes a de la serie\(\displaystyle \sum_{n=0}^∞a_nx^n\) están definidos por la relación de recurrencia\(a_n=\dfrac{a_{n−1}}{n}+\dfrac{a_{n−2}}{n(n−1)}\). Para\(a_0=0\) y\(a_1=1\), computar y trazar las sumas\(\displaystyle S_N=\sum_{n=0}^Na_nx^n\) para\(N=2,3,4,5\) on\([−1,1].\)

Contestar

La curva sólida es\(S_5\). La curva discontinua es\(S_2\), punteada es\(S_3\) y punteada es\(S_4\)

50) [T] Supongamos que los coeficientes a de la serie\(\displaystyle \sum_{n=0}^∞a_nx^n\) están definidos por la relación de recurrencia\(a_n=\dfrac{a_{n−1}}{\sqrt{n}}−\dfrac{a_{n−2}}{\sqrt{n(n−1)}}\). Para\(a_0=1\) y\(a_1=0\), computar y trazar las sumas\(\displaystyle S_N=\sum_{n=0}^Na_nx^n\) para\(N=2,3,4,5\) on\([−1,1]\).

51) [T] Dada la expansión de la serie de potencia\(\displaystyle \ln(1+x)=\sum_{n=1}^∞(−1)^{n−1}\frac{x^n}{n}\), determinar cuántos términos\(N\) de la suma evaluada en\(x=−1/2\) son necesarios para aproximar con\(\ln(2)\) precisión dentro de\(1/1000.\) Evaluar la suma parcial correspondiente\(\displaystyle \sum_{n=1}^N(−1)^{n−1}\frac{x^n}{n}\).

Contestar

Cuando\(\displaystyle x=−\frac{1}{2}, \;−\ln(2)=\ln\left(\frac{1}{2}\right)=−\sum_{n=1}^∞\frac{1}{n2^n}\). Dado\(\displaystyle \sum^∞_{n=11}\frac{1}{n2^n}<\sum_{n=11}^∞\frac{1}{2^n}=\frac{1}{2^{10}},\) que,\(\ln(2)=0.69314…;\) por lo\(\displaystyle \sum_{n=1}^{10}\frac{1}{n2^n}=0.69306…\) tanto,\(N=10.\)

52) [T] Dada la expansión de la serie de potencia\(\displaystyle \tan^{−1}(x)=\sum_{k=0}^∞(−1)^k\frac{x^{2k+1}}{2k+1}\), utilice la prueba de series alternas para determinar cuántos términos\(N\) de la suma evaluada en\(x=1\) son necesarios para aproximar con\(\tan^{−1}(1)=\frac{π}{4}\) precisión dentro de\(1/1000.\) Evaluar la suma parcial correspondiente\(\displaystyle \sum_{k=0}^N(−1)^k\frac{x^{2k+1}}{2k+1}\).

53) [T] Recordemos que\(\tan^{−1}\left(\frac{1}{\sqrt{3}}\right)=\frac{π}{6}.\) Asumiendo un valor exacto de\(\frac{1}{\sqrt{3}})\), estimar\(\frac{π}{6}\) evaluando sumas parciales de la expansión\(S_N\left(\frac{1}{\sqrt{3}}\right)\) de la serie de potencia\(\displaystyle \tan^{−1}(x)=\sum_{k=0}^∞(−1)^k\frac{x^{2k+1}}{2k+1}\) en\(x=\frac{1}{\sqrt{3}}\). ¿Cuál es el número más pequeño\(N\) tal que\(6S_N\left(\frac{1}{\sqrt{3}}\right)\) se aproxima\(π\) con precisión al interior\(0.001\)? ¿Cuántos términos se necesitan para que la precisión sea dentro\(0.00001\)?

Contestar

\(\displaystyle 6S_N\left(\frac{1}{\sqrt{3}}\right)=2\sqrt{3}\sum_{n=0}^N(−1)^n\frac{1}{3^n(2n+1).}\)Uno tiene\(π−6S_4\left(\frac{1}{\sqrt{3}}\right)=0.00101…\) y\(π−6S_5\left(\frac{1}{\sqrt{3}}\right)=0.00028…\) así\(N=5\) es la suma parcial más pequeña con precisión a dentro\(0.001.\) También,\(π−6S_7\left(\frac{1}{\sqrt{3}}\right)=0.00002…\) mientras\(π−6S_8\left(\frac{1}{\sqrt{3}}\right)=−0.000007…\) que también\(N=8\) es la más pequeña\(N\) para dar precisión a dentro\(0.00001.\)

Colaboradores

Template:ContribOpenStaxCalc