10.4E: Ejercicios para la Sección 10.4

Última actualización
Guardar como PDF

Page ID: 116134

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En los ejercicios 1 - 4, use sustituciones apropiadas para anotar la serie Maclaurin para el binomio dado.

1)$(1−x)^{1/3}$

2)$(1+x^2)^{−1/3}$

Responder: $\displaystyle (1+x^2)^{−1/3}=\sum_{n=0}^∞\left(n^{−\frac{1}{3}}\right)x^{2n}$

3)$(1−x)^{1.01}$

4)$(1−2x)^{2/3}$

Responder: $\displaystyle (1−2x)^{2/3}=\sum_{n=0}^∞(−1)^n2^n\left(n^{\frac{2}{3}}\right)x^n$

En los ejercicios 5 - 12, utilice la sustitución$(b+x)^r=(b+a)^r\left(1+\dfrac{x−a}{b+a}\right)^r$ en la expansión binomial para encontrar la serie Taylor de cada función con el centro dado.

5)$\sqrt{x+2}$ en$a=0$

6)$\sqrt{x^2+2}$ en$a=0$

Responder: $\displaystyle \sqrt{2+x^2}=\sum_{n=0}^∞2^{(1/2)−n}\left(n^{\frac{1}{2}}\right)x^{2n};(|x^2|<2)$

7)$\sqrt{x+2}$ en$a=1$

8)$\sqrt{2x−x^2}$ en$a=1$ (Pista:$2x−x^2=1−(x−1)^2$)

Responder: $\sqrt{2x−x^2}=\sqrt{1−(x−1)^2}$entonces$\displaystyle \sqrt{2x−x^2}=\sum_{n=0}^∞(−1)^n\left(n^{\frac{1}{2}}\right)(x−1)^{2n}$

9)$(x−8)^{1/3}$ en$a=9$

10)$\sqrt{x}$ en$a=4$

Responder: $\sqrt{x}=2\sqrt{1+\frac{x−4}{4}}$entonces$\displaystyle \sqrt{x}=\sum_{n=0}^∞2^{1−2n}\left(n^{\frac{1}{2}}\right)(x−4)^n$

11)$x^{1/3}$ en$a=27$

12)$\sqrt{x}$ en$x=9$

Responder: $\displaystyle \sqrt{x}=\sum_{n=0}^∞3^{1−3n}\left(n^{\frac{1}{2}}\right)(x−9)^n$

En los ejercicios 13 - 14, utilizar el teorema binomial para estimar cada número, calculando términos suficientes para obtener una estimación exacta a un error de como máximo$1/1000.$

13) [T]$(15)^{1/4}$ usando$(16−x)^{1/4}$

14) [T]$(1001)^{1/3}$ usando$(1000+x)^{1/3}$

Responder: $\displaystyle 10(1+\frac{x}{1000})^{1/3}=\sum_{n=0}^∞10^{1−3n}(^{\frac{1}{3}}_n)x^n$. Usando, por ejemplo, una estimación de cuarto grado en$x=1$ da$(1001)^{1/3}≈10\left(1+\left(1^{\frac{1}{3}}\right)10^{−3}+\left(2^{\frac{1}{3}}\right)10^{−6}+\left(3^{\frac{1}{3}}\right)10^{−9}+\left(3^{\frac{1}{3}}\right)10^{−12}\right)=10\left(1+\frac{1}{3.10^3}−\frac{1}{9.10^6}+\frac{5}{81.10^9}−\frac{10}{243.10^{12}}\right)=10.00333222...$ mientras que$(1001)^{1/3}=10.00332222839093....$ Dos términos serían suficientes para una precisión de tres dígitos.

En los ejercicios 15 - 18, utilice la aproximación binomial$\sqrt{1−x}≈1−\frac{x}{2}−\frac{x^2}{8}−\frac{x^3}{16}−\frac{5x^4}{128}−\frac{7x^5}{256}$ para$|x|<1$ aproximar cada número. Comparar este valor con el valor dado por una calculadora científica.

15) [T]$\frac{1}{\sqrt{2}}$ usando$x=\frac{1}{2}$ en$(1−x)^{1/2}$

16) [T]$\sqrt{5}=5×\frac{1}{\sqrt{5}}$ usando$x=\frac{4}{5}$ en$(1−x)^{1/2}$

Responder: La aproximación es$2.3152$; el valor CAS es$2.23….$

17) [T]$\sqrt{3}=\frac{3}{\sqrt{3}}$ usando$x=\frac{2}{3}$ en$(1−x)^{1/2}$

18) [T]$\sqrt{6}$ usando$x=\frac{5}{6}$ en$(1−x)^{1/2}$

Responder: La aproximación es$2.583…$; el valor CAS es$2.449….$

19) Integrar la aproximación binomial de$\sqrt{1−x}$ para encontrar una aproximación de$\displaystyle ∫^x_0\sqrt{1−t}\,dt$.

20) [T] Recordemos que la gráfica de$\sqrt{1−x^2}$ es un semicírculo superior de radio$1$. Integrar la aproximación binomial de$\sqrt{1−x^2}$ hasta orden$8$ de$x=−1$$x=1$ a estimación$\frac{π}{2}$.

Responder: $\sqrt{1−x^2}=1−\frac{x^2}{2}−\frac{x^4}{8}−\frac{x^6}{16}−\frac{5x^8}{128}+⋯.$Por lo tanto$\displaystyle ∫^1_{−1}\sqrt{1−x^2}\,dx=\left[x−\frac{x^3}{6}−\frac{x^5}{40}−\frac{x^7}{7⋅16}−\frac{5x^9}{9⋅128}+⋯\right]\Big|^1_{−1}≈2−\frac{1}{3}−\frac{1}{20}−\frac{1}{56}−\frac{10}{9⋅128}+error=1.590...$, mientras$\frac{π}{2}=1.570...$

En los ejercicios 21 - 24, utilice la expansión$(1+x)^{1/3}=1+\frac{1}{3}x−\frac{1}{9}x^2+\frac{5}{81}x^3−\frac{10}{243}x^4+⋯$ para escribir los primeros cinco términos (no necesariamente un polinomio cuártico) de cada expresión.

21)$(1+4x)^{1/3};\;a=0$

22)$(1+4x)^{4/3};\;a=0$

Responder: $(1+x)^{4/3}=(1+x)(1+\frac{1}{3}x−\frac{1}{9}x^2+\frac{5}{81}x^3−\frac{10}{243}x^4+⋯)=1+\frac{4x}{3}+\frac{2x^2}{9}−\frac{4x^3}{81}+\frac{5x^4}{243}+⋯$

23)$(3+2x)^{1/3};\;a=−1$

24)$(x^2+6x+10)^{1/3};\;a=−3$

Responder: $(1+(x+3)^2)^{1/3}=1+\frac{1}{3}(x+3)^2−\frac{1}{9}(x+3)^4+\frac{5}{81}(x+3)^6−\frac{10}{243}(x+3)^8+⋯$

25) Usar$(1+x)^{1/3}=1+\frac{1}{3}x−\frac{1}{9}x^2+\frac{5}{81}x^3−\frac{10}{243}x^4+⋯$ con$x=1$ para aproximar$2^{1/3}$.

26) Utilizar la aproximación$(1−x)^{2/3}=1−\frac{2x}{3}−\frac{x^2}{9}−\frac{4x^3}{81}−\frac{7x^4}{243}−\frac{14x^5}{729}+⋯$ para$|x|<1$ aproximar$2^{1/3}=2.2^{−2/3}$.

Responder: Dos veces la aproximación es$1.260…$ mientras$2^{1/3}=1.2599....$

27) Encuentra la$25^{\text{th}}$ derivada de$f(x)=(1+x^2)^{13}$ at$x=0$.

28) Encuentra la$99^{\text{th}}$ derivada de$f(x)=(1+x^4)^{25}$.

Responder: $f^{(99)}(0)=0$

En los ejercicios 29 - 36, encuentra la serie Maclaurin de cada función.

29)$f(x)=xe^{2x}$

30)$f(x)=2^x$

Responder: $\displaystyle \sum_{n=0}^∞\frac{(\ln(2)x)^n}{n!}$

31)$f(x)=\dfrac{\sin x}{x}$

32)$f(x)=\dfrac{\sin(\sqrt{x})}{\sqrt{x}},(x>0),$

Responder: Para$\displaystyle x>0,\, \sin(\sqrt{x})=\sum_{n=0}^∞(−1)^n\frac{x^{(2n+1)/2}}{\sqrt{x}(2n+1)!}=\sum_{n=0}^∞(−1)^n\frac{x^n}{(2n+1)!}$.

33)$f(x)=\sin(x^2)$

34)$f(x)=e^{x^3}$

Responder: $\displaystyle e^{x^3}=\sum_{n=0}^∞\frac{x^{3n}}{n!}$

35)$f(x)=\cos^2x$ usando la identidad$\cos^2x=\frac{1}{2}+\frac{1}{2}\cos(2x)$

36)$f(x)=\sin^2x$ usando la identidad$\sin^2x=\frac{1}{2}−\frac{1}{2}\cos(2x)$

Responder: $\displaystyle \sin^2x=−\sum_{k=1}^∞\frac{(−1)^k2^{2k−1}x^{2k}}{(2k)!}$

En los ejercicios 37 - 44, encuentra la serie Maclaurin de$\displaystyle F(x)=∫^x_0f(t)\,dt$ integrando la serie Maclaurin de$f$ término por término. Si no$f$ se define estrictamente en cero, puede sustituir el valor de la serie Maclaurin en cero.

37)$\displaystyle F(x)=∫^x_0e^{−t^2}\,dt;\; f(t)=e^{−t^2}=\sum_{n=0}^∞(−1)^n\frac{t^{2n}}{n!}$

38)$\displaystyle F(x)=\tan^{−1}x;\; f(t)=\frac{1}{1+t^2}=\sum_{n=0}^∞(−1)^nt^{2n}$

Responder: $\displaystyle \tan^{−1}x=\sum_{k=0}^∞\frac{(−1)^kx^{2k+1}}{2k+1}$

39)$\displaystyle F(x)=\tanh^{−1}x; \; f(t)=\frac{1}{1−t^2}=\sum_{n=0}^∞t^{2n}$

40)$\displaystyle F(x)=\sin^{−1}x; \; f(t)=\frac{1}{\sqrt{1−t^2}}=\sum_{k=0}^∞\left(k^{\frac{1}{2}}\right)\frac{t^{2k}}{k!}$

Responder: $\displaystyle \sin^{−1}x=\sum_{n=0}^∞\left(n^{\frac{1}{2}}\right)\frac{x^{2n+1}}{(2n+1)n!}$

41)$\displaystyle F(x)=∫^x_0\frac{\sin t}{t}\,dt; \; f(t)=\frac{\sin t}{t}=\sum_{n=0}^∞(−1)^n\frac{t^{2n}}{(2n+1)!}$

42)$\displaystyle F(x)=∫^x_0\cos\left(\sqrt{t}\right)\,dt; \; f(t)=\sum_{n=0}^∞(−1)^n\frac{x^n}{(2n)!}$

Responder: $\displaystyle F(x)=\sum_{n=0}^∞(−1)^n\frac{x^{n+1}}{(n+1)(2n)!}$

43)$\displaystyle F(x)=∫^x_0\frac{1−\cos t}{t^2}\,dt; \; f(t)=\frac{1−\cos t}{t^2}=\sum_{n=0}^∞(−1)^n\frac{t^{2n}}{(2n+2)!}$

44)$\displaystyle F(x)=∫^x_0\frac{\ln(1+t)}{t}\,dt; \; f(t)=\sum_{n=0}^∞(−1)^n\frac{t^n}{n+1}$

Responder: $\displaystyle F(x)=\sum_{n=1}^∞(−1)^{n+1}\frac{x^n}{n^2}$

En los ejercicios 45 - 52, computar al menos los tres primeros términos distintos de cero (no necesariamente un polinomio cuadrático) de la serie Maclaurin de$f$.

45)$f(x)=\sin\left(x+\frac{π}{4}\right)=\sin x\cos\left(\frac{π}{4}\right)+\cos x\sin\left(\frac{π}{4}\right)$

46)$f(x)=\tan x$

Responder: $x+\dfrac{x^3}{3}+\dfrac{2x^5}{15}+⋯$

47)$f(x)=\ln(\cos x)$

48)$f(x)=e^x\cos x$

Responder: $1+x−\dfrac{x^3}{3}−\dfrac{x^4}{6}+⋯$

49)$f(x)=e^{\sin x}$

50)$f(x)=\sec^2x$

Responder: $1+x^2+\dfrac{2x^4}{3}+\dfrac{17x^6}{45}+⋯$

51)$f(x)=\tanh x$

52)$f(x)=\dfrac{\tan\sqrt{x}}{\sqrt{x}}$ (ver expansión para$\tan x$)

Responder: Usando la expansión para$\tan x$ da$1+\dfrac{x}{3}+\dfrac{2x^2}{15}$.

En los ejercicios 53 - 56, encuentra el radio de convergencia de la serie Maclaurin de cada función.

53)$\ln(1+x)$

54)$\dfrac{1}{1+x^2}$

Responder: $\displaystyle \frac{1}{1+x^2}=\sum_{n=0}^∞(−1)^nx^{2n}$así$R=1$ por la prueba de relación.

55)$\tan^{−1}x$

56)$\ln(1+x^2)$

Responder: $\displaystyle \ln(1+x^2)=\sum_{n=1}^∞\frac{(−1)^{n−1}}{n}x^{2n}$así$R=1$ por la prueba de relación.

57) Encuentra la serie Maclaurin de$\sinh x=\dfrac{e^x−e^{−x}}{2}$.

58) Encuentra la serie Maclaurin de$\cosh x=\dfrac{e^x+e^{−x}}{2}$.

Responder: Agregar series de$e^x$ y$e^{−x}$ término por término. Términos impares cancelan y$\displaystyle \cosh x=\sum_{n=0}^∞\frac{x^{2n}}{(2n)!}$.

59) Diferenciar término por término la serie Maclaurin$\sinh x$ y comparar el resultado con la serie Maclaurin de$\cosh x$.

60) [T] Dejar$\displaystyle S_n(x)=\sum_{k=0}^n(−1)^k\frac{x^{2k+1}}{(2k+1)!}$ y$\displaystyle C_n(x)=\sum_{n=0}^n(−1)^k\frac{x^{2k}}{(2k)!}$ denotar los polinomios Maclaurin respectivos de grado$2n+1$ de$\sin x$ y grado$2n$ de$\cos x$. Trazar los errores$\dfrac{S_n(x)}{C_n(x)}−\tan x$ para$n=1,..,5$ y compararlos con$x+\dfrac{x^3}{3}+\dfrac{2x^5}{15}+\dfrac{17x^7}{315}−\tan x$ on$\left(−\frac{π}{4},\frac{π}{4}\right)$.

Responder

La relación$\dfrac{S_n(x)}{C_n(x)}$ se aproxima$\tan x$ mejor que$p_7(x)=x+\dfrac{x^3}{3}+\dfrac{2x^5}{15}+\dfrac{17x^7}{315}$ para$N≥3$. Las curvas discontinuas son$\dfrac{S_n}{C_n}−\tan x$ para$n=1,\, 2$. La curva punteada corresponde a$n=3$, y la curva punteada corresponde a$n=4$. La curva sólida es$p_7−\tan x$.

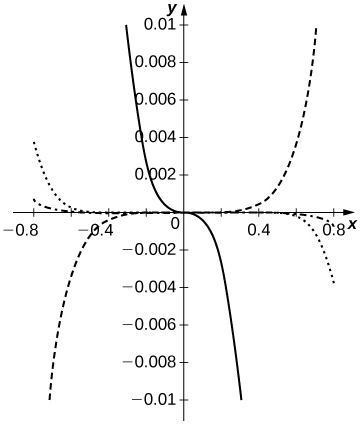
$Esta gráfica tiene dos curvas. La primera es una función decreciente que pasa por el origen. El segundo es una línea discontinua que es una función creciente que pasa por el origen. Las dos curvas están muy próximas alrededor del origen.$

61) Utilice la identidad$2\sin x\cos x=\sin(2x)$ para encontrar la expansión de la serie de potencia de$\sin^2x$ at$x=0$. (Pista: Integrar la serie Maclaurin de$\sin(2x)$ término por término.)

62) Si$\displaystyle y=\sum_{n=0}^∞a_nx^n$, encuentre las expansiones de la serie de potencia de$xy′$ y$x^2y''$.

Responder: Por el teorema de diferenciación término por término,$\displaystyle y′=\sum_{n=1}^∞na_nx^{n−1}$ así$\displaystyle y′=\sum_{n=1}^∞na_nx^{n−1}xy′=\sum_{n=1}^∞na_nx^n$, mientras que$\displaystyle y′=\sum_{n=2}^∞n(n−1)a_nx^{n−2}$ así$\displaystyle xy''=\sum_{n=2}^∞n(n−1)a_nx^n$.

63) [T] Supongamos que$\displaystyle y=\sum_{k=0}^∞a^kx^k$ satisface$y′=−2xy$ y$y(0)=0$. Demuéstralo$a_{2k+1}=0$ para todos$k$ y eso$a_{2k+2}=\dfrac{−a_{2k}}{k+1}$. Trazar la suma parcial$S_{20}$ de$y$ en el intervalo$[−4,4]$.

64) [T] Supongamos que un conjunto de puntajes de exámenes estandarizados se distribuye normalmente con media$μ=100$ y desviación estándar$σ=10$. Establecer una integral que represente la probabilidad de que una puntuación de prueba esté entre$90$$110$ y y usar la integral del grado polinomio de$10$ Maclaurin$\frac{1}{\sqrt{2π}}e^{−x^2/2}$ para estimar esta probabilidad.

Responder: La probabilidad es$\displaystyle p=\frac{1}{\sqrt{2π}}∫^{(b−μ)/σ}_{(a−μ)/σ}e^{−x^2/2}\,dx$ dónde$a=90$ y$b=100$, es decir,$\displaystyle p=\frac{1}{\sqrt{2π}}∫^1_{−1}e^{−x^2/2}\,dx=\frac{1}{\sqrt{2π}}∫^1_{−1}\sum_{n=0}^5(−1)^n\frac{x^{2n}}{2^nn!}\,dx=\frac{2}{\sqrt{2π}}\sum_{n=0}^5(−1)^n\frac{1}{(2n+1)2^nn!}≈0.6827.$

65) [T] Supongamos que un conjunto de puntajes de exámenes estandarizados se distribuye normalmente con media$μ=100$ y desviación estándar$σ=10$. Establecer una integral que represente la probabilidad de que una puntuación de prueba esté entre$70$$130$ y y usar la integral del grado polinomio de$50$ Maclaurin$\frac{1}{\sqrt{2π}}e^{−x^2/2}$ para estimar esta probabilidad.

66) [T] Supongamos que$\displaystyle \sum_{n=0}^∞a_nx^n$ converge a una función$f(x)$ tal que$f(0)=1,\, f′(0)=0$, y$f''(x)=−f(x)$. Encuentre una fórmula para$a_n$ y trazar la suma parcial$S_N$ para$N=20$ on$[−5,5].$

Responder

Al igual que en el problema anterior se obtiene$a_n=0$ si$n$ es impar y$a_n=−(n+2)(n+1)a_{n+2}$ si$n$ es par, así$a_0=1$ lleva a$a_{2n}=\dfrac{(−1)^n}{(2n)!}$.

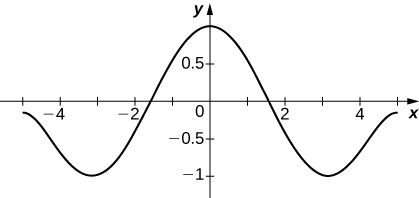
$Esta gráfica es una curva de onda simétrica sobre el origen. Tiene un pico a y = 1 por encima del origen. Tiene los puntos más bajos en -3 y 3.$

67) [T] Supongamos que$\displaystyle \sum_{n=0}^∞a_nx^n$ converge a una función$f(x)$ tal que$f(0)=0,\; f′(0)=1$, y$f''(x)=−f(x)$. Encuentra una fórmula para an y traza la suma parcial$S_N$ para$N=10$ on$[−5,5]$.

68) Supongamos que$\displaystyle \sum_{n=0}^∞a_nx^n$ converge a una función$y$ tal que$y''−y′+y=0$ donde$y(0)=1$ y$y'(0)=0.$ Encuentra una fórmula que se relaciona$a_{n+2},\;a_{n+1},$ y una y computa$a_0,...,a_5$.

Responder: $\displaystyle y''=\sum_{n=0}^∞(n+2)(n+1)a_{n+2}x^n$y$\displaystyle y′=\sum_{n=0}^∞(n+1)a_{n+1}x^n$ así$y''−y′+y=0$ implica eso$(n+2)(n+1)a_{n+2}−(n+1)a_{n+1}+a_n=0$ o$a_n=\dfrac{a_{n−1}}{n}−\dfrac{a_{n−2}}{n(n−1)}$ para todos$n⋅y(0)=a_0=1$ y$y′(0)=a_1=0,$ así$a_2=\frac{1}{2},\;a_3=\frac{1}{6}\;,a_4=0$, y$a_5=−\frac{1}{120}$.

69) Supongamos que$\displaystyle \sum_{n=0}^∞a_nx^n$ converge a una función$y$ tal que$y''−y′+y=0$ donde$y(0)=0$ y$y′(0)=1$. Encuentre una fórmula que se$a_{n+2},\;a_{n+1}$ relacione, y un y compute$a_1,...,a_5$.

El error al aproximar la integral$\displaystyle ∫^b_af(t)\, dt$ por la de una aproximación de Taylor$\displaystyle ∫^b_aPn(t) \,dt$ es como mucho$\displaystyle ∫^b_aR_n(t) \,dt$. En los ejercicios 70 - 71, la estimación del resto de Taylor$R_n≤\frac{M}{(n+1)!}|x−a|^{n+1}$ garantiza que la integral del polinomio Taylor del orden dado se aproxima a la integral de$f$ con un error menor que$\frac{1}{10}$.

a. Evaluar la integral del polinomio Taylor apropiado y verificar que se aproxime al valor CAS con un error menor que$\frac{1}{100}$.

b. Comparar la precisión de la estimación integral polinomial con la estimación del resto.

70) [T]$\displaystyle ∫^π_0\frac{\sin t}{t}\, dt;\quad P_s=1−\frac{x^2}{3!}+\frac{x^4}{5!}−\frac{x^6}{7!}+\frac{x^8}{9!}$ (Se puede suponer que el valor absoluto de la novena derivada de$\frac{\sin t}{t}$ está delimitado por$0.1$.)

Responder: a. (Prueba)
b. Tenemos$R_s≤\frac{0.1}{(9)!}π^9≈0.0082<0.01.$ Tenemos$\displaystyle ∫^π_0\left(1−\frac{x^2}{3!}+\frac{x^4}{5!}−\frac{x^6}{7!}+\frac{x^8}{9!}\right)\,dx=π−\frac{π^3}{3⋅3!}+\frac{π^5}{5⋅5!}−\frac{π^7}{7⋅7!}+\frac{π^9}{9⋅9!}=1.852...,$ mientras que$\displaystyle ∫^π_0\frac{\sin t}{t}\,dt=1.85194...$, por lo que el error real es aproximadamente$0.00006.$

71) [T]$\displaystyle ∫^2_0e^{−x^2}\,dx;\; p_{11}=1−x^2+\frac{x^4}{2}−\frac{x^6}{3!}+⋯−\frac{x^{22}}{11!}$ (Se puede suponer que el valor absoluto de la$23^{\text{rd}}$ derivada de$e^{−x^2}$ es menor que$2×10^{14}$.)

Los siguientes ejercicios (72-73) tratan sobre integrales de Fresnel.

72) Las integrales de Fresnel se definen por$\displaystyle C(x)=∫^x_0\cos(t^2)\,dt$ y$\displaystyle S(x)=∫^x_0\sin(t^2)\,dt$. Calcular la serie de potencia de$C(x)$$S(x)$ y y trazar las sumas$C_N(x)$ y$S_N(x)$ de los primeros términos$N=50$ distintos de cero en$[0,2π]$.

Responder

Desde$\displaystyle \cos(t^2)=\sum_{n=0}^∞(−1)^n\frac{t^{4n}}{(2n)!}$ y$\displaystyle \sin(t^2)=\sum_{n=0}^∞(−1)^n\frac{t^{4n+2}}{(2n+1)!}$, uno tiene$\displaystyle S(x)=\sum_{n=0}^∞(−1)^n\frac{x^{4n+3}}{(4n+3)(2n+1)!}$ y$\displaystyle C(x)=\sum_{n=0}^∞(−1)^n\frac{x^{4n+1}}{(4n+1)(2n)!}$. Las sumas de los primeros términos$50$ distintos de cero se trazan a continuación con$C_{50}(x)$ la curva sólida y$S_{50}(x)$ la curva discontinua.

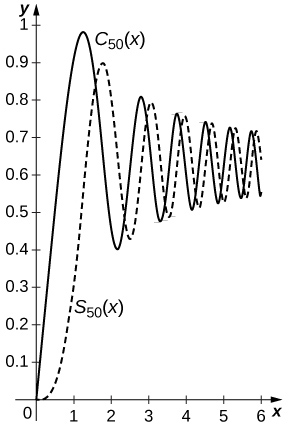
$Esta gráfica tiene dos curvas. El primero es una curva sólida etiquetada Csub50 (x). Comienza en el origen y es una onda que disminuye gradualmente en amplitud. El más alto que alcanza es y = 1. La segunda curva está etiquetada como Ssub50 (x). Se trata de una onda que disminuye gradualmente en amplitud. El más alto que alcanza es 0.9. Se encuentra muy cerca del patrón de la primera curva con un ligero desplazamiento hacia la derecha.$

73) [T] Las integrales de Fresnel se utilizan en aplicaciones de diseño para carreteras y ferrocarriles y otras aplicaciones debido a las propiedades de curvatura de la curva con coordenadas$(C(t),S(t))$. Trazar la curva$(C_{50},S_{50})$ para$0≤t≤2π$, cuyas coordenadas se calcularon en el ejercicio anterior.

74) Estimar$\displaystyle ∫^{1/4}_0\sqrt{x−x^2}\,dx$ aproximando$\sqrt{1−x}$ usando la aproximación binomial$\displaystyle 1−\frac{x}{2}−\frac{x^2}{8}−\frac{x^3}{16}−\frac{5x^4}{2128}−\frac{7x^5}{256}$.

Responder: $\displaystyle ∫^{1/4}_0\sqrt{x}\left(1−\frac{x}{2}−\frac{x^2}{8}−\frac{x^3}{16}−\frac{5x^4}{128}−\frac{7x^5}{256}\right)\,dx =\frac{2}{3}2^{−3}−\frac{1}{2}\frac{2}{5}2^{−5}−\frac{1}{8}\frac{2}{7}2^{−7}−\frac{1}{16}\frac{2}{9}2^{−9}−\frac{5}{128}\frac{2}{11}2^{−11}−\frac{7}{256}\frac{2}{13}2^{−13}=0.0767732...$mientras que$\displaystyle ∫^{1/4}_0\sqrt{x−x^2}\, dx=0.076773.$

75) [T] Utilice la aproximación de Newton del binomio$\sqrt{1−x^2}$ para aproximarse de la$π$ siguiente manera. El círculo centrado en$(\frac{1}{2},0)$ con radio$\frac{1}{2}$ tiene semicírculo superior$y=\sqrt{x}\sqrt{1−x}$. El sector de este círculo delimitado por el$x$ -eje entre$x=0$ y$x=\frac{1}{2}$ y por la línea que une$(\frac{1}{4},\frac{\sqrt{3}}{4})$ corresponde a$\frac{1}{6}$ del círculo y tiene área$\frac{π}{24}$. Este sector es la unión de un triángulo rectángulo con altura$\frac{\sqrt{3}}{4}$ y base$\frac{1}{4}$ y la región debajo de la gráfica entre$x=0$ y$x=\frac{1}{4}$. Para encontrar el área de esta región se puede escribir$y=\sqrt{x}\sqrt{1−x}=\sqrt{x}×(\text{binomial expansion of} \sqrt{1−x})$ e integrar término por término. Utilice este enfoque con la aproximación binomial del ejercicio anterior para estimar$π$.

76) Utilizar la aproximación$T≈2π\sqrt{\frac{L}{g}}(1+\frac{k^2}{4})$ para aproximar el periodo de un péndulo que tiene$10$ metros de longitud y ángulo máximo$θ_{max}=\frac{π}{6}$ donde$k=\sin\left(\frac{θ_{max}}{2}\right)$. Compare esto con la estimación de ángulo pequeño$T≈2π\sqrt{\frac{L}{g}}$.

Responder: $T≈2π\sqrt{\frac{10}{9.8}}\left(1+\frac{\sin^2(θ/12)}{4}\right)≈6.453$segundos. La estimación de ángulo pequeño es$T≈2π\sqrt{\frac{10}{9.8}≈6.347}$. El error relativo es de alrededor$2$ por ciento.

77) Supongamos que un péndulo es tener un periodo de$2$ segundos y un ángulo máximo de$θ_{max}=\frac{π}{6}$. Se usa$T≈2π\sqrt{\dfrac{L}{g}}\left(1+\dfrac{k^2}{4}\right)$ para aproximar la longitud deseada del péndulo. ¿Qué longitud predice la estimación de ángulo pequeño$T≈2π\sqrt{\frac{L}{g}}$?

78) Evaluar$\displaystyle ∫^{π/2}_0\sin^4θ\,dθ$ en la aproximación$\displaystyle T=4\sqrt{\frac{L}{g}}∫^{π/2}_0\left(1+\frac{1}{2}k^2\sin^2θ+\frac{3}{8}k^4\sin^4θ+⋯\right)\,dθ$ para obtener una estimación mejorada para$T$.

Responder: $\displaystyle ∫^{π/2}_0\sin^4θ\, dθ=\frac{3π}{16}.$De ahí$T≈2π\sqrt{\frac{L}{g}}\left(1+\frac{k^2}{4}+\frac{9}{256}k^4\right).$

79) [T] Una fórmula equivalente para el periodo de un péndulo con amplitud$\displaystyle θ_{max}$ es$T(θ_{max})=2\sqrt{2}\sqrt{\frac{L}{g}}∫^{θ_{max}}_0\frac{dθ}{\sqrt{\cos θ}−\cos(θ_{max})}$ donde$L$ está la longitud del péndulo y$g$ es la constante de aceleración gravitacional. Cuando$θ_{max}=\frac{π}{3}$ lleguemos$\dfrac{1}{\sqrt{\cos t−1/2}}≈\sqrt{2}\left(1+\frac{t^2}{2}+\frac{t^4}{3}+\frac{181t^6}{720}\right)$. Integrar esta aproximación para estimar$T(\frac{π}{3})$ en términos de$L$ y$g$. Suponiendo$g=9.806$ metros por segundo al cuadrado, encuentra una longitud aproximada$L$ tal que$T(\frac{π}{3})=2$ segundos.

Colaboradores

Template:ContribOpenStaxCalc