12.3E: Ejercicios para la Sección 12.3

Última actualización
Guardar como PDF

Page ID: 116127

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Para los ejercicios 1-4,$\vecs{v}$ se dan los vectores$\vecs{u}$ y. Calcular el producto punto$\vecs{u}\cdot\vecs{v}$.

1)$\quad \vecs{u}=⟨3,0⟩, \quad \vecs{v}=⟨2,2⟩$

Contestar: $\vecs{u}\cdot\vecs{v}=6$

2)$\quad \vecs{u}=⟨3,−4⟩, \quad \vecs{v}=⟨4,3⟩$

3)$\quad \vecs{u}=⟨2,2,−1⟩, \quad \vecs{v}=⟨−1,2,2⟩$

Contestar: $\vecs{u}\cdot\vecs{v}=0$

4)$\quad \vecs{u}=⟨4,5,−6⟩, \quad \vecs{v}=⟨0,−2,−3⟩$

Para los ejercicios 5-8, se$\vecs{c}$ dan los vectores$\vecs{a}, \,\vecs{b}$, y. Determinar los vectores$(\vecs{a}\cdot\vecs{b})\vecs{c}$ y$(\vecs{a}⋅\vecs{c})\vecs{b}.$ expresar los vectores en forma de componentes.

5)$\quad \vecs{a}=⟨2,0,−3⟩, \quad \vecs{b}=⟨−4,−7,1⟩, \quad \vecs{c}=⟨1,1,−1⟩$

Contestar: $ (\vecs a⋅\vecs b)\vecs c=⟨−11,−11,11⟩; (\vecs a⋅\vecs c)\vecs b=⟨−20,−35,5⟩$

6)$\quad \vecs{a}=⟨0,1,2⟩, \quad \vecs{b}=⟨−1,0,1⟩, \quad \vecs{c}=⟨1,0,−1⟩$

7)$\quad \vecs{a}=\mathbf{\hat i} +\mathbf{\hat j} , \quad \vecs{b}=\mathbf{\hat i} −\mathbf{\hat k} , \quad \vecs{c}=\mathbf{\hat i} −2\mathbf{\hat k} $

Contestar: $ (\vecs a⋅\vecs b)\vecs c=⟨1,0,−2⟩; (\vecs a⋅\vecs c)\vecs b=⟨1,0,−1⟩$

8)$\quad \vecs{a}=\mathbf{\hat i} −\mathbf{\hat j} +\mathbf{\hat k} , \quad \vecs{b}=\mathbf{\hat j} +3\mathbf{\hat k} , \quad \vecs{c}=−\mathbf{\hat i} +2\mathbf{\hat j} −4\mathbf{\hat k} $

Para los ejercicios 9-12, se dan dos vectores.

a. Encuentra la medida del ángulo$θ$ entre estos dos vectores. Exprese la respuesta en radianes redondeados a dos decimales, si no es posible expresarla exactamente.

b. ¿Es$θ$ un ángulo agudo?

9) [T]$\quad \vecs{a}=⟨3,−1⟩, \quad \vecs{b}=⟨−4,0⟩$

Contestar: $ a. θ=2.82$rad; no$ b. θ$ es agudo.

10) [T]$\quad \vecs{a}=⟨2,1⟩, \quad \vecs{b}=⟨−1,3⟩$

11)$\quad \vecs{u}=3\mathbf{\hat i}, \quad \vecs{v}=4\mathbf{\hat i} +4\mathbf{\hat j} $

Contestar: $ a. θ=\frac{π}{4}$rad;$ b. θ$ es agudo.

12)$\quad \vecs{u}=5\mathbf{\hat i}, \quad \vecs{v}=−6\mathbf{\hat i} +6\mathbf{\hat j} $

Para los ejercicios 13-18, encontrar la medida del ángulo entre los vectores tridimensionales$\vecs{a}$ y$\vecs{b}$. Exprese la respuesta en radianes redondeados a dos decimales, si no es posible expresarla exactamente.

13)$\quad \vecs{a}=⟨3,−1,2⟩, \quad \vecs{b}=⟨1,−1,−2⟩$

Contestar: $ θ=\frac{π}{2}$

14)$\quad \vecs{a}=⟨0,−1,−3⟩, \quad \vecs{b}=⟨2,3,−1⟩$

15)$\quad \vecs{a}=\mathbf{\hat i} +\mathbf{\hat j} , \quad \vecs{b}=\mathbf{\hat j} −\mathbf{\hat k} $

Contestar: $ θ=\frac{π}{3}$

16)$\quad \vecs{a}=\mathbf{\hat i} −2\mathbf{\hat j} +\mathbf{\hat k} , \quad \vecs{b}=\mathbf{\hat i} +\mathbf{\hat j} −2\mathbf{\hat k} $

17) [T]$\quad \vecs{a}=3\mathbf{\hat i} −\mathbf{\hat j} −2\mathbf{\hat k} , \quad \vecs{b}=\vecs v+\vecs w,$ dónde$\quad \vecs{v}=−2\mathbf{\hat i} −3\mathbf{\hat j} +2\mathbf{\hat k} $ y$\vecs{w}=\mathbf{\hat i} +2\mathbf{\hat k} $

Contestar: $ θ=2$rad

18) [T]$\quad \vecs{a}=3\mathbf{\hat i} −\mathbf{\hat j} +2\mathbf{\hat k} , \quad \vecs{b}=\vecs v−\vecs w,$ dónde$\quad \vecs{v}=2\mathbf{\hat i} +\mathbf{\hat j} +4\mathbf{\hat k} $ y$\vecs{w}=6\mathbf{\hat i} +\mathbf{\hat j} +2\mathbf{\hat k} $

Para los ejercicios 19-22, determinar si los vectores dados son ortogonales.

19)$\quad \vecs{a}=⟨x,y⟩, \quad \vecs{b}=⟨−y, x⟩$, donde$x$ y$y$ son números reales distintos de cero

Contestar: Ortogonal

20)$\quad \vecs{a}=⟨x, x⟩, \quad \vecs{b}=⟨−y, y⟩$, donde$x$ y$y$ son números reales distintos de cero

21)$\quad \vecs{a}=3\mathbf{\hat i} −\mathbf{\hat j} −2\mathbf{\hat k} , \quad \vecs{b}=−2\mathbf{\hat i} −3\mathbf{\hat j} +\mathbf{\hat k} $

Contestar: No ortogonal

22)$\quad \vecs{a}=\mathbf{\hat i} −\mathbf{\hat j} , \quad \vecs{b}=7\mathbf{\hat i} +2\mathbf{\hat j} −\mathbf{\hat k} $

23) Buscar todos los vectores bidimensionales$\vecs a$ ortogonales al vector$ \vecs b=⟨3,4⟩.$ Expresar la respuesta en forma de componente.

Contestar: $ \vecs a=⟨−\frac{4α}{3},α⟩,$donde$ α≠0$ es un numero real

24) Encontrar todos los vectores bidimensionales$ \vecs a$ ortogonales al vector$ \vecs b=⟨5,−6⟩.$ Expresar la respuesta mediante el uso de vectores unitarios estándar.

25) Determinar todos los vectores tridimensionales$ \vecs u$ ortogonales al vector$ \vecs v=⟨1,1,0⟩.$ Expresar la respuesta usando vectores unitarios estándar.

Contestar: $ \vecs u=−α\mathbf{\hat i} +α\mathbf{\hat j} +β\mathbf{\hat k} ,$donde$ α$ y$ β$ son números reales tales que$ α^2+β^2≠0$

26) Determinar todos los vectores tridimensionales$\vecs u$ ortogonales al vector$\vecs v=\mathbf{\hat i} −\mathbf{\hat j} −\mathbf{\hat k} $. Exprese la respuesta en forma de componentes.

27) Determinar el número real$α$ tal que los vectores$\vecs a=2\mathbf{\hat i} +3\mathbf{\hat j} $ y$\vecs b=9\mathbf{\hat i} +α\mathbf{\hat j} $ son ortogonales.

Contestar: $α=−6$

28) Determinar el número real$α$ tal que los vectores$\vecs a=−3\mathbf{\hat i} +2\mathbf{\hat j} $ y$\vecs b=2\mathbf{\hat i} +α\mathbf{\hat j} $ son ortogonales.

29) [T] Considerar los puntos$P(4,5)$ y$Q(5,−7)$, y señalar que$O$ representa el origen.

a. Determinar vectores$\vecd{OP}$ y$\vecd{OQ}$. Exprese la respuesta usando vectores unitarios estándar.

b. Determinar la medida del ángulo$O$ en triángulo$OPQ$. Exprese la respuesta en grados redondeados a dos decimales.

Contestar: $a. \vecd{OP}=4\mathbf{\hat i} +5\mathbf{\hat j} , \quad \vecd{OQ}=5\mathbf{\hat i} −7\mathbf{\hat j} ; \quad b. 105.8°$

30) [T] Considerar puntos$ A(1,1), B(2,−7),$ y$C(6,3)$.

a. Determinar vectores$ \vecd{BA}$ y$\vecd{BC}$. Exprese la respuesta en forma de componentes.

b. Determinar la medida del ángulo$B$ en triángulo$ABC$. Exprese la respuesta en grados redondeados a dos decimales.

31) Determine la medida del ángulo$A$ en triángulo$ABC$, donde$A(1,1,8), B(4,−3,−4),$ y$C(−3,1,5).$ exprese su respuesta en grados redondeados a dos decimales.

Contestar: $68.33°$

32) Considerar puntos$P(3,7,−2)$ y$Q(1,1,−3).$ Determinar el ángulo entre vectores$\vecd{OP}$ y$\vecd{OQ}$. [Recuerda que$O$ representa el origen.] Exprese la respuesta en grados redondeados a dos decimales.

Para los ejercicios 33-34, determine cuáles (si los hay) pares de los siguientes vectores son ortogonales.

33)$\quad\vecs u=⟨3,7,−2⟩, \quad \vecs v=⟨5,−3,−3⟩, \quad \vecs w=⟨0,1,−1⟩$

Contestar: $\vecs u$y$\vecs v$ son ortogonales;$\vecs v$ y$\vecs w$ son ortogonales, pero$\vecs u$ y no$\vecs w$ son ortogonales.

34)$\quad\vecs u=\mathbf{\hat i} −\mathbf{\hat k} , \quad \vecs v=5\mathbf{\hat j} −5\mathbf{\hat k} , \quad \vecs w=10\mathbf{\hat j} $

35) Usa vectores para mostrar que un paralelogramo con diagonales iguales es un rectángulo.

36) Usa vectores para mostrar que las diagonales de un rombo son perpendiculares.

37) Demostrar que$\vecs u⋅(\vecs v+\vecs w)=\vecs u⋅\vecs v+\vecs u⋅\vecs w$ es cierto para cualquier vector$\vecs u, \vecs v$, y$\vecs w$.

38) Verificar la identidad$\vecs u⋅(\vecs v+\vecs w)=\vecs u⋅\vecs v+\vecs u⋅\vecs w$ para vectores$\vecs u=⟨1,0,4⟩, \vecs v=⟨−2,3,5⟩,$ y$\vecs w=⟨4,−2,6⟩$.

Para los ejercicios 39-41, determinar$\vecs u\cdot\vecs v$ utilizando la información dada.

39)$\quad\|\vecs u\| = 5$,$\quad\|\vecs v\| = 3$, y el ángulo entre$\vecs u$ y$\vecs v$ es$\pi/6$ rad.

Contestar: $\vecs u \cdot \vecs v = (5)(3)\cos \frac{\pi}{6} = 15\cdot\frac{\sqrt{3}}{2} = \frac{15\sqrt{3}}{2} $

40)$\quad\|\vecs u\| = 20$,$\quad\|\vecs v\| = 15$, y el ángulo entre$\vecs u$ y$\vecs v$ es$5\pi/4$ rad.

41)$\quad\|\vecs u\| = 7$,$\quad\|\vecs v\| = 12$, y el ángulo entre$\vecs u$ y$\vecs v$ es$\pi/2$ rad.

Contestar: $\vecs u \cdot \vecs v = (7)(12)\cos \frac{\pi}{2} = 84\cdot0 = 0 $

42) Considerando la definición del producto punto,$\vecs u\cdot\vecs v = \|\vecs u\|\|\vecs v\|\cos \theta$, dónde$\theta$ está el ángulo entre$\vecs u$ y$\vecs v$, qué se puede decir sobre el ángulo$\theta$ entre dos vectores distintos de cero$\vecs u$ y$\vecs v$ si:

a.$\quad\vecs u \cdot \vecs v > 0$?

b.$\quad\vecs u \cdot \vecs v < 0$?

c.$\quad\vecs u \cdot \vecs v = 0$?

En los ejercicios 43-45, se te dan los vértices de un triángulo. Use productos punteados para determinar si cada triángulo es agudo, obtuso o derecho.

43)$\quad (2, 3, 0), \, (3, 1, -2), \, (-1, 4, 5)$

Contestar: Etiquetar los puntos$P$,$Q$ y$R$. Después determinar los vectores$\vecd{PQ}$ y$\vecd{PR}$.
Aquí vemos eso, si$P = (2, 3, 0), \, Q = (3, 1, -2)$ y$R = (-1, 4, 5)$, así tenemos$\vecd{PQ} = <1,-2,-2>$ y$\vecd{PR} = <-3,1,5>$.
Entonces$\vecd{PQ} \cdot \vecd{PR} = -15 < 0$, entonces el ángulo$QPR$ es obtuso. Por lo tanto, este triángulo debe ser un triángulo obtuso.

44)$\quad (5, 1, 0), \, (7, 1, 1), \, (6, 3, 2)$

45)$\quad (6, 1, 4), \, (3, 2, -1), \, (2, 3, 1)$

Solución:: Etiquetar los puntos$P$,$Q$ y$R$. Después determinar los vectores$\vecd{PQ}$ y$\vecd{PR}$.
Aquí vemos eso, si$P = (6, 1, 4), \, Q = (3, 2, -1)$ y$R = (2, 3, 1)$, así tenemos$\vecd{PQ} = <-3,1,-5>$ y$\vecd{PR} = <-4,2,-3>$.
Entonces$\vecd{PQ} \cdot \vecd{PR} = 29 > 0$, entonces el ángulo$QPR$ es agudo. Este triángulo aún podría ser cualquiera de los tres tipos, por lo que necesitamos verificar otro ángulo.
Considerando ángulo$PQR$ encontramos$\vecd{QP} = <3,-1,5>$ y$\vecd{QR} = <-1,1,2>$, así$\vecd{QP} \cdot \vecd{QR} = 6 > 0$, mostrar ángulo también$PQR$ es agudo.
Luego debemos verificar el tercer ángulo para determinar si se trata de un triángulo rectángulo o de un triángulo agudo.
Para comprobar ángulo$PRQ$ nos encontramos$\vecd{RP} = <4,-2,3>$ y$\vecd{RQ} = <1,-1,-2>$, dándonos$\vecd{RP} \cdot \vecd{RQ} = 0$. $PRQ$El ángulo es así un ángulo recto.
Por lo tanto este triángulo es un triángulo rectángulo.

46) Cuáles de las siguientes operaciones están permitidas para vectores distintos de cero$\vecs u$$\vecs v$,$\vecs w$, y, y cuáles no. Explica tu razonamiento.

a.$\vecs u + \left(\vecs v \cdot \vecs w\right)$ b.$\left(\vecs u \cdot \vecs v\right) \cdot \vecs w$ c.$\left(\vecs u \cdot \vecs v\right) \vecs w$
d.$\left(\vecs u + \vecs v\right) \cdot \vecs w$ e.$\left(\vecs u + \vecs v\right) \cdot \|\vecs w\|$ f.$\|\vecs u + \vecs v\| \|\vecs w\|$

Proyecciones

Para los ejercicios 47-50, dados los vectores$\vecs u$ y$\vecs v$:

a. Encuentra la proyección vectorial$\text{Proj}_\vecs{u}\vecs v$ de vector$\vecs v$ sobre vector$\vecs u$ y el componente de$\vecs v$ ese es ortogonal a$\vecs u$, es decir,$\vecs v_\text{perp}$. Exprese sus respuestas en forma de componentes.

b. Encontrar la proyección escalar$\text{comp}_\vecs{u}\vecs v = \| \text{Proj}_\vecs{u}\vecs v \|$ de vector$\vecs v$ sobre vector$\vecs u$.

c. Encuentra la proyección vectorial$\text{Proj}_\vecs{v}\vecs u$ de vector$\vecs u$ sobre vector$\vecs v$ y el componente de$\vecs u$ ese es ortogonal a$\vecs v$, es decir,$\vecs u_\text{perp}$. Exprese sus respuestas en forma de vector unitario.

d. Encontrar la proyección escalar$\text{comp}_\vecs{v}\vecs u$ de vector$\vecs u$ sobre vector$\vecs v$.

47)$\quad\vecs u=5\mathbf{\hat i} +2\mathbf{\hat j} , \quad \vecs v=2\mathbf{\hat i} +3\mathbf{\hat j} $

Contestar: a.$\text{Proj}_\vecs{u}\vecs v =⟨\frac{80}{29},\frac{32}{29}⟩$ y$\vecs v_\text{perp} = <-\frac{22}{29}, \frac{55}{29}>$; b.$\text{comp}_\vecs{u}\vecs v=\frac{16}{\sqrt{29}} = \frac{16\sqrt{29}}{29};$
c.$\text{Proj}_\vecs{v}\vecs u = \frac{32}{13}\mathbf{\hat i} + \frac{48}{13}\mathbf{\hat j} $ y$\vecs u_\text{perp} = \frac{33}{13}\mathbf{\hat i} - \frac{22}{13}\mathbf{\hat j} $; d.$\text{comp}_\vecs{v}\vecs u=\frac{16}{\sqrt{13}}=\frac{16\sqrt{13}}{13}$

48)$\quad\vecs u=⟨−4,7⟩,\quad \vecs v=⟨3,5⟩$

49)$\quad\vecs u=3\mathbf{\hat i} +2\mathbf{\hat k} , \quad \vecs v=2\mathbf{\hat j} +4\mathbf{\hat k} $

Contestar: a.$\text{Proj}_\vecs{u}\vecs v =⟨\frac{24}{13},0,\frac{16}{13}⟩$ y$\vecs v_\text{perp} = <-\frac{24}{13}, 2, \frac{36}{13}>$; b.$\text{comp}_\vecs{u}\vecs v=\frac{8}{\sqrt{13}}=\frac{8\sqrt{13}}{13}$
c.$\text{Proj}_\vecs{v}\vecs u =\frac{4}{5}\mathbf{\hat j} + \frac{8}{5}\mathbf{\hat k} $ y$\vecs u_\text{perp} = 3\mathbf{\hat i} - \frac{4}{5}\mathbf{\hat j} + \frac{2}{5}\mathbf{\hat k} $; d.$\text{comp}_\vecs{v}\vecs u=\frac{\sqrt{80}}{5} = \frac{4\sqrt{5}}{5};$

50)$\quad\vecs u=⟨4,4,0⟩, \quad \vecs v=⟨0,4,1⟩$

51) Considerar los vectores$\vecs u=4\mathbf{\hat i} −3\mathbf{\hat j} $ y$\vecs v=3\mathbf{\hat i} +2\mathbf{\hat j} .$

a. Encuentra la forma componente del vector$\text{Proj}_\vecs{u}\vecs v$ que representa la proyección de$\vecs v$ sobre$\vecs u$.

b. escribir la descomposición$\vecs v=\vecs w+\vecs q$ del vector$\vecs v$ en los componentes ortogonales$\vecs w$ y$\vecs q$, donde$\vecs w$ es la proyección de$\vecs v$ sobre$\vecs u$ y$\vecs q$ es el componente vectorial de$\vecs v$ ortogonal a la dirección de$\vecs u$. Es decir,$ \vecs q = \vecs v_\text{perp}$.

Contestar: a.$\text{Proj}_\vecs{u}\vecs v=⟨\frac{24}{25},−\frac{18}{25}⟩$; b.$\vecs q = \vecs v_\text{perp} =⟨\frac{51}{25},\frac{68}{25}⟩$,
$\vecs v =\vecs w+\vecs q= \text{Proj}_\vecs{u}\vecs v + \vecs v_\text{perp} =⟨\frac{24}{25},−\frac{18}{25}⟩+⟨\frac{51}{25},\frac{68}{25}⟩$
Entonces tenemos eso,$\vecs v = ⟨\frac{24}{25},−\frac{18}{25}⟩+⟨\frac{51}{25},\frac{68}{25}⟩$.

52) Considerar vectores$\vecs u=2\mathbf{\hat i} +4\mathbf{\hat j} $ y$\vecs v=4\mathbf{\hat j} +2\mathbf{\hat k} .$

a. Encuentra la forma componente del vector$\vecs w=\text{Proj}_\vecs{u}\vecs v$ que representa la proyección de$\vecs v$ sobre$\vecs u$.

53) Un camión$50,000$ de libras está estacionado en una colina con una$5°$ pendiente por encima de la horizontal (en la$x$ dirección positiva). Considerando solo la fuerza debida a la gravedad, encuentra

a. el componente del peso del camión que está tirando del camión cuesta abajo (alineado con la carretera)

b. el componente del peso del camión que es perpendicular a la carretera.

c. la magnitud de la fuerza necesaria para evitar que el camión ruede cuesta abajo

d. la magnitud de la fuerza que es perpendicular a la carretera.

Solución:: Dejar$\vecs F$ ser la fuerza debida a la gravedad sobre el camión (su peso) y dejar$\vecs r$ ser la unidad vector apuntando arriba de la colina a la derecha.

Entonces
a. el componente del peso del camión que está tirando del camión cuesta abajo es$\text{Proj}_\vecs{r}\vecs F$.
Ahora$\vecs F = -50,000\mathbf{\hat j} \quad\text{and}\quad \vecs r = \cos 5°\,\mathbf{\hat i} + \sin 5°\,\mathbf{\hat j} $ y$\vecs F\cdot\vecs r = -50,000\sin 5° \approx -4357.78714$
Tenga en cuenta eso$\|\vecs r\| = 1$.
Entonces:$\quad\,\text{Proj}_\vecs{r}\vecs F = \left(\frac{\vecs F\cdot\vecs r}{\|\vecs r\|^2}\right)\vecs r \quad = \left(-50,000\sin 5°\right)\vecs r \quad=\quad -50000\sin 5° \cos 5° \,\mathbf{\hat i} - 50000\sin^2 5° \,\mathbf{\hat j} $.
Usando la identidad,$\sin 2\theta = 2\cos \theta \sin \theta$, podemos simplificar esto como
$\text{Proj}_\vecs{r}\vecs F = -25000\sin 10° \,\mathbf{\hat i} - 50000\sin^2 5°\, \mathbf{\hat j} \quad\approx\quad -4341.2\,\mathbf{\hat i} - 379.8\,\mathbf{\hat j} $.

b. el componente del peso del camión que es perpendicular a la carretera es$\vecs F_\text{perp}$.
Ya que sabemos eso$\vecs F = \text{Proj}_\vecs{r}\vecs F+\vecs F_\text{perp}$, tenemos eso$\vecs F_\text{perp} = \vecs F - \text{Proj}_\vecs{r}\vecs F$.
Entonces$\quad \vecs F_\text{perp} = -50000\mathbf{\hat j} - \left( -25000\sin 10° \,\mathbf{\hat i} - 50000\sin^2 5°\, \mathbf{\hat j} \right)$
$= 25000\sin 10° \,\mathbf{\hat i} + \left(50000\sin^2 5° - 50000\right)\mathbf{\hat j} = 25000\sin 10° \,\mathbf{\hat i} - 50000\cos^2 5° \,\mathbf{\hat j} \quad\approx\quad 4341.2\,\mathbf{\hat i} - 49620.2\,\mathbf{\hat j} $.

c. la magnitud de la fuerza necesaria para evitar que el camión ruede cuesta abajo es$\| \text{Proj}_\vecs{r}\vecs F \| = 50,000\sin 5°$ lbs$\approx 4357.8$ lbs. Tenga en cuenta que esta fuerza es en realidad la negativa del vector de proyección, pero su magnitud es la misma.

d. la magnitud del peso del camión que es perpendicular a la carretera es$ \| \vecs F_\text{perp} \| \approx 49809.7$ lbs.

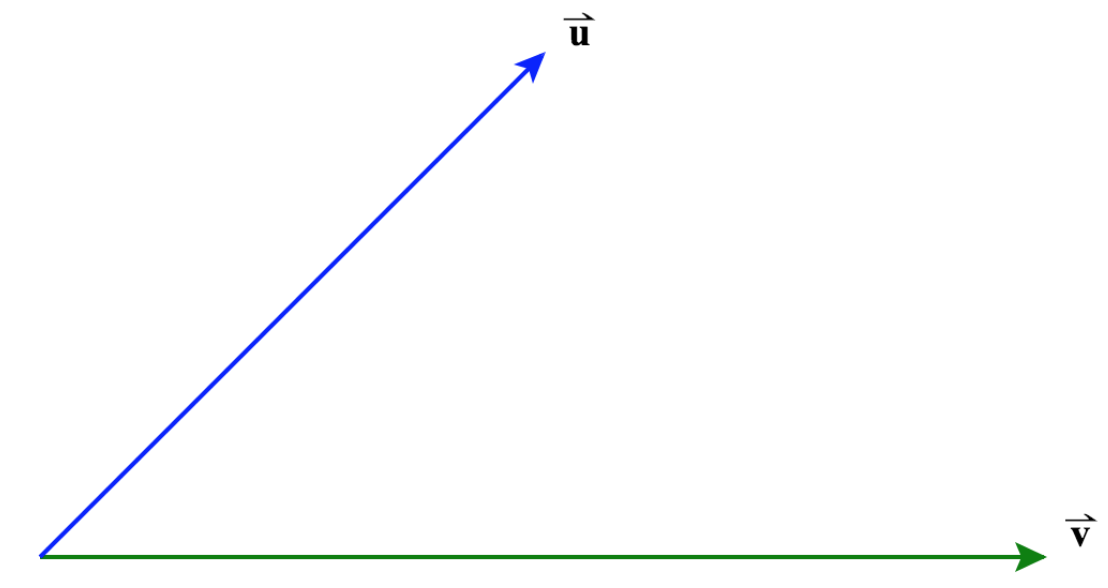
54) Dados los vectores$\vecs u$ y$\vecs v$ mostrados en cada diagrama a continuación, dibuje$\text{Proj}_\vecs{v}\vecs u$ y$ \vecs u_\text{perp} $.

$acuteAngle.png$ $obtuseAngle.png$

Trabajo

55) Encontrar el trabajo realizado por fuerza$\vecs F=⟨5,6,−2⟩$ (medida en Newtons) que mueve una partícula de punto$P(3,−1,0)$ a punto a$Q(2,3,1)$ lo largo de una línea recta (la distancia se mide en metros).

Contestar: $17\,\text{N⋅m}$

56) [T] Se tira de un trineo ejerciendo una fuerza de 100 N sobre una cuerda que hace un ángulo de$25°$ con la horizontal. Encuentra el trabajo realizado al tirar del trineo 40 m. (Redondear la respuesta a un decimal.)

57) [T] Un padre está tirando de su hijo en un trineo en ángulo$20°$ con la horizontal con una fuerza de 25 lb (ver la siguiente imagen). Él tira del trineo en un camino recto de 50 pies. ¿Cuánto trabajo hizo el hombre que tiraba del trineo? (Redondear la respuesta al entero más cercano.)

Contestar: 1175 ftlb

58) [T] Un carro es remolcado con una fuerza de 1600 N. La cuerda utilizada para tirar del carro hace un ángulo de 25° con la horizontal. Encuentra el trabajo realizado en el remolque del auto a 2 km. Exprese la respuesta en julios ($1$J$=1$ nm) redondeados al entero más cercano.

59) [T] Un barco navega hacia el norte ayudado por un viento que sopla en una dirección de$ N30°E$ con una magnitud de 500 lb. ¿Cuánto trabajo realiza el viento a medida que la embarcación se mueve 100 pies? (Redondear la respuesta a dos decimales.)

Contestar: $25000\sqrt{3}$ft-lbs$\approx 43,301.27$ ft-lbs

Solución:: Vector que representa el viento:$\vecs w = 500\cos 60^{\circ} \mathbf{\hat i} + 500\sin 60^{\circ} \mathbf{\hat j}$
Vector que representa el desplazamiento hacia el norte:$\vecs d = 100 \mathbf{\hat j}$
Trabajo realizado por el viento:$W = \vecs w \cdot \vecs d = 25000\sqrt{3}$ ft-lbs$\approx 43,301.27$ ft-lbs

Otras aplicaciones del producto Dot

60) [T] Encuentra los vectores que unen el centro de un reloj a las horas 1:00, 2:00, y 3:00. Supongamos que el reloj es circular con un radio de 1 unidad.

61) Una molécula de metano tiene un átomo de carbono situado en el origen y cuatro átomos de hidrógeno ubicados en puntos$P(1,1,−1),Q(1,−1,1),R(−1,1,1),$ y$S(−1,−1,−1)$ (ver figura).

a. Encontrar la distancia entre los átomos de hidrógeno ubicados en$P$ y$R$.

b. Encontrar el ángulo entre vectores$\vecd{OS}$ y$\vecd{OR}$ que conectan el átomo de carbono con los átomos de hidrógeno ubicados en$S$ y$R$, que también se llama ángulo de enlace. Exprese la respuesta en grados redondeados a dos decimales.

Contestar: $a. 2\sqrt{2}; \quad b. 109.47°$

62) Vector$\vecs p=⟨150,225,375⟩$ representa el precio de ciertos modelos de bicicletas vendidas por una tienda de bicicletas. Vector$\vecs n=⟨10,7,9⟩$ representa el número de bicicletas vendidas de cada modelo, respectivamente. Calcular el producto punto$\vecs p⋅\vecs n$ y exponer su significado.

63) [T] Dos fuerzas$\vecs F_1$ y$\vecs F_2$ están representadas por vectores con puntos iniciales que están en el origen. La primera fuerza tiene una magnitud de 20 lb y pasa por el punto$P(1,1,0)$. La segunda fuerza tiene una magnitud de 40 lb y pasa por el punto$Q(0,1,1)$. $\vecs F$Dejen ser la resultante fuerza de fuerzas$\vecs F_1$ y$\vecs F_2$.

a. Encontrar la magnitud de$\vecs F$. (Redondear la respuesta a un decimal.)

b. encontrar los ángulos de dirección de$\vecs F$. (Exprese la respuesta en grados redondeados a un decimal.)

Contestar: $ a. ∥\vecs F_1+\vecs F_2∥=52.9$lb; b. Los ángulos de dirección son$α=74.5°,\,β=36.7°,$ y$ γ=57.7°.$

64) [T] Considerar$\vecs r(t)=⟨\cos t,\sin t,2t⟩$ el vector de posición de una partícula en el tiempo$t∈[0,30]$, donde los componentes de$\vecs r$ se expresan en centímetros y el tiempo en segundos. Dejar$\vecd{OP}$ ser el vector de posición de la partícula después de 1 seg.

a. mostrar que todos los vectores$\vecd{PQ}$, donde$Q(x,y,z)$ es un punto arbitrario, ortogonal al vector$\vecs v(1)$ de velocidad instantánea de la partícula después de 1 seg, se pueden expresar como$ \vecd{PQ}=⟨x−\cos 1,y−\sin 1,z−2⟩$, donde$x\sin 1−y\cos 1−2z+4=0.$ El conjunto de puntos$Q$ describe un plano llamado el plano normal a la trayectoria de la partícula en el punto$P$.

b. utilizar un CAS para visualizar el vector de velocidad instantánea y el plano normal en el punto$P$ junto con la trayectoria de la partícula.

Colaboradores

Template:ContribOpenStaxCalc

Los problemas 39-46 y 53 y 54 fueron creados por Paul Seeburger (Monroe Community College).
Solución al Problema 59 también fue agregado por Paul Seeburger.