12.5: Ecuaciones de líneas y planos en el espacio

Objetivos de aprendizaje

• Escriba las ecuaciones vectoriales, paramétricas y simétricas de una línea a través de un punto dado en una dirección dada, y una línea a través de dos puntos dados.
• Encuentra la distancia desde un punto hasta una línea determinada.
• Escribe las ecuaciones vectoriales y escalares de un plano a través de un punto dado con una normal dada.
• Encuentra la distancia desde un punto hasta un plano determinado.
• Encuentra el ángulo entre dos planos.

Por ahora, estamos familiarizados con la escritura de ecuaciones que describen una línea en dos dimensiones. Para escribir una ecuación para una línea, debemos conocer dos puntos en la línea, o debemos conocer la dirección de la línea y al menos un punto por el que pasa la línea. En dos dimensiones, utilizamos el concepto de pendiente para describir la orientación, o dirección, de una línea. En tres dimensiones, describimos la dirección de una línea usando un vector paralelo a la línea. En esta sección, examinamos cómo usar ecuaciones para describir líneas y planos en el espacio.

Ecuaciones para una línea en el espacio

Primero vamos a explorar lo que significa que dos vectores sean paralelos. Recordemos que los vectores paralelos deben tener direcciones iguales u opuestas. Si dos vectores distintos de cero\( \vecs{v}\),\( \vecs{u}\) y, son paralelos, afirmamos que debe haber un escalar,\( k\), tal que\( \vecs{u}=k\vecs{v}\). Si\( \vecs{u}\) y\( \vecs{v}\) tienen la misma dirección, simplemente elija

\[ k=\dfrac{‖\vecs{u}‖}{‖\vecs{v}‖}. \nonumber \]

Si\( \vecs{u}\) y\( \vecs{v}\) tienen direcciones opuestas, elija

\[ k=−\dfrac{‖\vecs{u}‖}{‖\vecs{v}‖}. \nonumber \]

Tenga en cuenta que lo contrario también se sostiene. Si\( \vecs{u}=k \vecs{v}\) para algún escalar\( k\), entonces cualquiera\( \vecs{u}\) y\(\vecs{ v}\) tener la misma dirección\( (k>0)\) u direcciones opuestas\( (k<0)\), así\( \vecs{u}\) y\( \vecs{v}\) son paralelas. Por lo tanto, dos vectores distintos de cero\( \vecs{u}\) y\(\vecs{ v}\) son paralelos si y solo si\( \vecs{u}=k\vecs{v}\) para algún escalar\( k\). Por convención,\( \vecs{0}\) se considera que el vector cero es paralelo a todos los vectores.

Figura\(\PageIndex{1}\): Vector\(\vecs{v}\) es el vector de dirección para\( \vecd{PQ}\).

Al igual que en dos dimensiones, podemos describir una línea en el espacio utilizando un punto en la línea y la dirección de la línea, o un vector paralelo, al que llamamos vector de dirección (Figura\(\PageIndex{1}\)). Dejar\( L\) ser una línea en el espacio pasando por punto\( P(x_0,y_0,z_0)\). Dejar\( \vecs{v}=⟨a,b,c⟩\) ser un vector paralelo a\( L\). Entonces, para cualquier punto en línea\( Q(x,y,z)\), sabemos que\( \vecd{PQ}\) es paralelo a\( \vecs{v}\). Así, como acabamos de discutir, hay un escalar,\( t\), tal que\( \vecd{PQ}=t\vecs{v}\), que da

\ [\ begin {align}\ vecd {PQ} &=t\ vecs {v}\ nonumber\\ [4pt] +52
x−x_0, y−y_0, z−z_0⟩ &=tìa, b, c⟩\ nonumber\\ [4pt] +52
x−x_0, y−y_0, z−z_0⟩ &=⟩ tb, tc⟩. \ label {eq1}\ end {align}\]

Usando operaciones vectoriales, podemos reescribir la ecuación\ ref {eq1}

\ [\ begin {alinear*} +52 x−x_0, y−y_0, z−z_0⟩ &=+52 ta, tb, tc⟩\\ [4pt] +52
x, y, z−+52, y_0, z_0⟩ &=t⟩ A, b, c⟩\\ [4pt]
\ underbrackets {+52 x, y, z⟩} _ {\ vecs {r}} &=\ underbrackets {2+x_0, y_0, z_0⟩} _ {\ vecs {r} _o} +t\ underbrackets {2+a, b, c⟩} _ {\ vecs {v}}. \ end {alinear*}\]

Ajuste\( \vecs{r}=⟨x,y,z⟩\) y\( \vecs{r}_0=⟨x_0,y_0,z_0⟩\), ahora tenemos la ecuación vectorial de una línea:

\[ \vecs{r}=\vecs{r}_0+t\vecs{v}. \label{vector} \]

Equiparando componentes, Ecuación\ ref {vector} muestra que las siguientes ecuaciones son simultáneamente verdaderas:\( x−x_0=ta, y−y_0=tb,\) y\( z−z_0=tc.\) Si resolvemos cada una de estas ecuaciones para las variables componentes\( x,y,\) y\( z\), obtenemos un conjunto de ecuaciones en las que cada variable se define en términos del parámetro \(t\)y que, en conjunto, describen la línea. Este conjunto de tres ecuaciones forma un conjunto de ecuaciones paramétricas de una línea:

\[ x=x_0+ta \nonumber \]

\[ y=y_0+tb \nonumber \]

\[ z=z_0+tc.\nonumber \]

Si resolvemos cada una de las ecuaciones para\( t\) asumir\( a,b\), y\( c\) son distintos de cero, obtenemos una descripción diferente de la misma línea:

\[ \begin{align*} \dfrac{x−x_0}{a} =t \\[4pt] \dfrac{y−y_0}{b} =t \\[4pt] \dfrac{z−z_0}{c} =t.\end{align*}\]

Debido a que cada expresión es igual\(t\), todas tienen el mismo valor. Podemos establecerlos iguales entre sí para crear ecuaciones simétricas de una línea:

\[\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}. \nonumber \]

Resumimos los resultados en el siguiente teorema.

Teorema: Ecuaciones paramétricas y simétricas de una línea

Una línea\( L\) paralela al vector\( \vecs{v}=⟨a,b,c⟩\) y que pasa a través del punto se\( P(x_0,y_0,z_0)\) puede describir mediante las siguientes ecuaciones paramétricas:

\[ x=x_0+ta, y=y_0+tb, \nonumber \]

y

\[ z=z_0+tc. \nonumber \]

Si las constantes\( a,b,\) y\( c\) son todas distintas de cero, entonces se\( L\) pueden describir mediante la ecuación simétrica de la línea:

\[\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}. \nonumber \]

Las ecuaciones paramétricas de una línea no son únicas. El uso de un vector paralelo diferente o un punto diferente en la línea conduce a una representación diferente y equivalente. Cada conjunto de ecuaciones paramétricas conduce a un conjunto relacionado de ecuaciones simétricas, por lo que se deduce que una ecuación simétrica de una línea tampoco es única.

Ejemplo\( \PageIndex{1}\): Equations of a Line in Space

Encuentra ecuaciones paramétricas y simétricas de la línea que pasa por puntos\( (1,4,−2)\) y\( (−3,5,0).\)

Solución

Primero, identificar un vector paralelo a la línea:

\[ \vecs v=⟨−3−1,5−4,0−(−2)⟩=⟨−4,1,2⟩. \nonumber \]

Utilice cualquiera de los puntos dados en la línea para completar las ecuaciones paramétricas:

\[\begin{align*} x =1−4t \\[4pt] y =4+t, \end{align*}\]

y

\[ z=−2+2t. \nonumber \]

Resuelve cada ecuación\( t\) para crear la ecuación simétrica de la línea:

\[ \dfrac{x−1}{−4}=y−4=\dfrac{z+2}{2}. \nonumber \]

Ejercicio\( \PageIndex{1}\)

Encuentra ecuaciones paramétricas y simétricas de la línea que pasa por puntos\( (1,−3,2)\) y\( (5,−2,8).\)

Pista:

Comienza por encontrar un vector paralelo a la línea.

Contestar

Posible conjunto de ecuaciones paramétricas: conjunto\( x=1+4t,\; y=−3+t,\; z=2+6t;\) relacionado de ecuaciones simétricas:\[ \dfrac{x−1}{4}=y+3=\dfrac{z−2}{6} \nonumber \]

A veces no queremos la ecuación de una línea entera, solo un segmento de línea. En este caso, limitamos los valores de nuestro parámetro\( t\). Por ejemplo, let\( P(x_0,y_0,z_0)\) y\( Q(x_1,y_1,z_1)\) be puntos en una línea, y let\( \vecs p=⟨x_0,y_0,z_0⟩\) y\( \vecs q=⟨x_1,y_1,z_1⟩\) ser los vectores de posición asociados. Además, vamos\(\vecs r=⟨x,y,z⟩\). Queremos encontrar una ecuación vectorial para el segmento de línea entre\( P\) y\( Q\). Usando\( P\) como nuestro punto conocido en la línea, y\( \vecd{PQ}=⟨x_1−x_0,y_1−y_0,z_1−z_0⟩\) como la ecuación del vector de dirección, la ecuación\ ref {vector} da

\[\vecs{r}=\vecs{p}+t(\vecd{PQ}). \label{eq10} \]

La ecuación\ ref {eq10} se puede expandir usando las propiedades de los vectores:

\ [\ begin {align*}\ vecs {r} &=\ vecs {p} +t (\ vecd {PQ})\\ [4pt]
&=+52 x_0, y_0, z_0+t+52 x_1−x_0, y_1−y_0, z_1−z_0⟩\\ [4pt]
&=+52 x_0, y_0, z_0+t (+52 x_1, y_1, z_1−+52 x_0, y_0, z_0⟩)\\ [4pt]
&=+52 x_0, y_0, z_0+t+52 x_1, y_1, z_1−t2+x_0, y_0, z_0⟩\\ [4pt]
& =( 1−t) 2_0, y_0 , z_0+t⟩ x_1, y_1, z_1⟩\\ [4pt]
& =( 1−t)\ vecs {p} +t\ vecs {q}. \ end {alinear*}\]

Así, la ecuación vectorial de la línea que pasa a través\( P\) y\( Q\) es

\[\vecs{r}=(1−t)\vecs{p}+t\vecs{q}. \nonumber \]

Recuerda que no queríamos la ecuación de toda la línea, solo el segmento de línea entre\( P\) y\( Q\). Observe que cuando\( t=0\), tenemos\(\vecs{r}=\vecs{p}\), y cuando\( t=1\), tenemos\( \vecs r=\vecs q\). Por lo tanto, la ecuación vectorial del segmento de línea entre\( P\) y\( Q\) es

\[\vecs{r}=(1−t)\vecs{p}+t\vecs{q},0≤t≤1. \nonumber \]

Volviendo a la Ecuación\ ref {vector}, también podemos encontrar ecuaciones paramétricas para este segmento de línea. Tenemos

\ [\ begin {align*}\ vecs {r} &=\ vecs {p} +t (\ vecd {PQ})\\ [4pt] +52
x, y, z⟩ &=+52 x_0, y_0, z_0+t+52 x_1−x_0, y_1−y_0, z_1−z_0⟩\\ [4pt]
&=x_0+t (x_1−x_0), y_0+t (y_1−y_0), z_0+t (z_1−z_0) ⟩. \ end {alinear*}\]

Entonces, las ecuaciones paramétricas son

\[ \begin{align*} x &=x_0+t(x_1−x_0) \\[4pt] y &=y_0+t(y_1−y_0) \\[4pt] z &=z_0+t(z_1−z_0), \quad 0≤t≤1. \end{align*} \label{para} \]

Ejemplo\( \PageIndex{2}\): Parametric Equations of a Line Segment

Encuentra ecuaciones paramétricas del segmento de línea entre los puntos\( P(2,1,4)\) y\( Q(3,−1,3).\)

Solución

Comience con las ecuaciones paramétricas para una línea (Ecuaciones\ ref {para}) y trabaje con cada componente por separado:

\[ \begin{align*} x &=x_0+t(x_1−x_0)\\[4pt] &=2+t(3−2)\\[4pt] &=2+t, \end{align*}\]

\[ \begin{align*} y &=y_0+t(y_1−y_0)\\[4pt] &=1+t(−1−1)\\[4pt] &=1−2t, \end{align*}\]

y

\[ \begin{align*} z &=z_0+t(z_1−z_0)\\[4pt] &=4+t(3−4)\\[4pt] &=4−t. \end{align*}\]

Por lo tanto, las ecuaciones paramétricas para el segmento de línea son

\[ \begin{align*} x &=2+t\\[4pt] y &=1−2t\\[4pt] z &=4−t,\quad 0≤t≤1.\end{align*}\]

Ejercicio\( \PageIndex{2}\)

Encuentra ecuaciones paramétricas del segmento de línea entre puntos\( P(−1,3,6)\) y\( Q(−8,2,4)\).

Contestar

\( x=−1−7t,\; y=3−t,\; z=6−2t, \quad 0≤t≤1 \)

Distancia entre un punto y una línea

Ya sabemos calcular la distancia entre dos puntos en el espacio. Ahora ampliamos esta definición para describir la distancia entre un punto y una línea en el espacio. Existen varios contextos del mundo real cuando es importante poder calcular estas distancias. Al construir una casa, por ejemplo, los constructores deben considerar los requisitos de “retroceso”, cuando las estructuras o accesorios tienen que estar a cierta distancia de la línea de propiedad. El viaje aéreo ofrece otro ejemplo. Las aerolíneas están preocupadas por las distancias entre las áreas pobladas y las rutas de vuelo propuestas.

Dejar\( L\) ser una línea en el plano y dejar\( M\) ser cualquier punto no en la línea. Luego, definimos\( d\) distancia de\( M\) a\( L\) como la longitud del segmento de línea\( \overline{MP}\), donde\( P\) es un punto sobre\( L\) tal que\( \overline{MP}\) es perpendicular a\( L\) (Figura\(\PageIndex{2}\)).

Figura\(\PageIndex{2}\): La distancia de punto\( M\) a línea\( L\) es la longitud de\( \overline{MP}\).

Cuando buscamos la distancia entre una línea y un punto en el espacio, la Figura\(\PageIndex{2}\) sigue aplicándose. Seguimos definiendo la distancia como la longitud del segmento de línea perpendicular que conecta el punto a la línea. En el espacio, sin embargo, no hay una manera clara de saber qué punto de la línea crea tal segmento de línea perpendicular, por lo que seleccionamos un punto arbitrario en la línea y usamos propiedades de vectores para calcular la distancia. Por lo tanto, dejar\( P\) ser un punto arbitrario en línea\( L\) y dejar\(\vecs{v}\) ser un vector de dirección para\( L\) (Figura\(\PageIndex{3}\)).

Figura\(\PageIndex{3}\): Vectores\( \vecd{PM}\) y\( \vecs{v}\) forman dos lados de un paralelogramo con base\( ‖\vecs v‖\) y altura\( d\), que es la distancia entre una línea y un punto en el espacio.

Vectores\( \vecd{PM}\) y\(\vecs{v}\) forman dos lados de un paralelogramo con área\( ‖\vecd{PM}×\vecs{v}‖\). Usando una fórmula a partir de la geometría, el área de este paralelogramo también se puede calcular como el producto de su base y altura:

\[‖\vecd{PM}×\vecs{v}‖=‖\vecs v‖d. \nonumber \]

Podemos usar esta fórmula para encontrar una fórmula general para la distancia entre una línea en el espacio y cualquier punto que no esté en la línea.

Distancia de un punto a una línea

Dejar\( L\) ser una línea en el espacio que pasa por punto\( P\) con vector de dirección\(\vecs{v}\). Si algún punto no\( M\) está encendido\( L\), entonces la distancia de\( M\) a\( L\) es

\[d=\dfrac{‖\vecd{PM}×\vecs{v}‖}{‖\vecs{v}‖}. \nonumber \]

Ejemplo\( \PageIndex{3}\): Calculating the Distance from a Point to a Line

Encuentra la distancia entre el punto\( M=(1,1,3)\) y la línea\( \dfrac{x−3}{4}=\dfrac{y+1}{2}=z−3.\)

Solución:

A partir de las ecuaciones simétricas de la línea, sabemos que vector\( \vecs{v}=⟨4,2,1⟩\) es un vector de dirección para la línea. Al establecer las ecuaciones simétricas de la línea iguales a cero, vemos que el punto\( P(3,−1,3)\) se encuentra en la línea. Entonces,

\[\begin{align*} \vecd{PM} =⟨1−3,1−(−1),3−3⟩\\[4pt] =⟨−2,2,0⟩. \end{align*}\]

Para calcular la distancia, necesitamos encontrar\( \vecd{PM}×\vecs v:\)

\ [\ begin {align*}\ vecd {PM} ×\ vecs {v} &=\ begin {vmatrix}\ mathbf {\ hat i} &\ mathbf {\ hat j} &\ mathbf {\ hat k}\\ −2 & 2 & 0\ 4 & 2 & 1\ end {vmatrix}\\ [4pt] &= (2−0)\ mathbf {\ hat i} − (−2−0)\ mathbf {\ hat j} + (−4−8)\ mathbf {\ hat k}\\ [4pt]
&=2\ mathbf {\ hat i} +2\ mathbf {\ hat j} −12\ mathbf {\ hat k}. \ end {alinear*}\]

Por lo tanto, la distancia entre el punto y la línea es (Figura\(\PageIndex{4}\))

\ [\ begin {align*} d &=\ dfrac {‖\ vecd {PM} ×\ vecs {v} ‖} {‖\ vecs {v} ‖}\\ [4pt]
&=\ dfrac {\ sqrt {2^2+2^2+12^2}} {\ sqrt {4^2+2^2+1^2}}\\ [4pt]
&=\ dfrac {2\ sqrt {38}} {\ sqrt {21}}\\ [4pt]
&=\ dfrac {2\ sqrt {798}} {21}\,\ texto {unidades}\ final {alinear*}\]

Figura\(\PageIndex{4}\):\( (1,1,3)\) El punto es aproximadamente\( 2.7\) unidades de la línea con ecuaciones simétricas\( \dfrac{x−3}{4}=\dfrac{y+1}{2}=z−3.\)

Ejercicio\( \PageIndex{3}\)

Encuentra la distancia entre el punto\( (0,3,6)\) y la línea con ecuaciones paramétricas\( x=1−t,\; y=1+2t,\; z=5+3t.\)

Pista

Encuentre un vector con punto inicial\( (0,3,6)\) y un punto terminal en la línea, y luego busque un vector de dirección para la línea.

Contestar

\( \sqrt{\dfrac{10}{7}} = \dfrac{\sqrt{70}}{7} \,\text{units} \)

Relaciones entre líneas

Dadas dos líneas en el plano bidimensional, las líneas son iguales, son paralelas pero no iguales, o se cruzan en un solo punto. En tres dimensiones, es posible un cuarto caso. Si dos líneas en el espacio no son paralelas, pero no se cruzan, entonces se dice que las líneas son líneas sesgadas (Figura\(\PageIndex{5}\)).

Figura\(\PageIndex{5}\): En tres dimensiones, es posible que dos líneas no se crucen, incluso cuando tienen diferentes direcciones.

Para clasificar las líneas como paralelas pero no iguales, iguales, intersecantes o sesgadas, necesitamos saber dos cosas: si los vectores de dirección son paralelos y si las líneas comparten un punto (Figura\(\PageIndex{6}\)).

Figura\(\PageIndex{6}\): Determinar la relación entre dos líneas en función de si sus vectores de dirección son paralelos y si comparten un punto.

Ejemplo\( \PageIndex{4}\): Classifying Lines in Space

Para cada par de líneas, determine si las líneas son iguales, paralelas pero no iguales, sesgadas o intersectadas.

a.

• \( L_1:\; x=2s−1, \; y=s−1, \; z=s−4\)
• \( L_2: \; x=t−3, \; y=3t+8, \; z=5−2t\)

b.

• \( L_1: \; x=−y=z\)
• \( L_2:\; \dfrac{x−3}{2}=y=z−2\)

c.

• \( L_1:\; x=6s−1,\; y=−2s,\; z=3s+1\)
• \( L_2:\; \dfrac{x−4}{6}=\dfrac{y+3}{−2}=\dfrac{z−1}{3}\)

Solución

a.\( L_1\) La línea tiene un vector de dirección\( \vecs v_1=⟨2,1,1⟩\); la línea\( L_2\) tiene un vector de dirección\( \vecs v_2=⟨1,3,−2⟩\). Debido a que los vectores de dirección no son vectores paralelos, las líneas se cruzan o sesgan. Para determinar si las líneas se cruzan, vemos si hay un punto,\( (x,y,z)\), que yace en ambas líneas. Para encontrar este punto, utilizamos las ecuaciones paramétricas para crear un sistema de igualdades:

\[ 2s−1=t−3; \nonumber \]

\[ s−1=3t+8; \nonumber \]

\[ s−4=5−2t. \nonumber \]

Por la primera ecuación,\( t=2s+2.\) Sustituir en la segunda ecuación rinde

\( s−1=3(2s+2)+8\)

\( s−1=6s+6+8\)

\( 5s=−15\)

\( s=−3.\)

La sustitución en la tercera ecuación, sin embargo, produce una contradicción:

\( s−4=5−2(2s+2)\)

\( s−4=5−4s−4\)

\( 5s=5\)

\( s=1.\)

No hay un punto único que satisfaga las ecuaciones paramétricas para\( L_1\) y\( L_2\) simultáneamente. Estas líneas no se cruzan, por lo que están sesgadas (ver la siguiente figura).

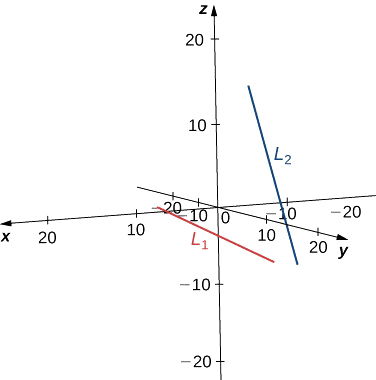
b.\( L_1\) La línea tiene vector de dirección\( \vecs v_1=⟨1,−1,1⟩\) y pasa por el origen,\( (0,0,0)\). \( L_2\)La línea tiene un vector de dirección diferente\( \vecs v_2=⟨2,1,1⟩\), por lo que estas líneas no son paralelas ni iguales. Let\( r\) representa el parámetro para la línea\( L_1\) y let\(s\) representar el parámetro para\( L_2\):

\[\begin{align*} &\text{Line }L_1: & & \text{Line }L_2:\\[4pt] &x = r & & x = 2s + 3\\[4pt] &y = -r & & y = s \\[4pt] &z = r & & z = s + 2 \end{align*}\]

Resolver el sistema de ecuaciones para encontrar\( r=1\) y\( s=−1\). Si necesitamos encontrar el punto de intersección, podemos sustituir estos parámetros en las ecuaciones originales para obtener\( (1,−1,1)\) (ver la siguiente figura).

c. Líneas\( L_1\) y\( L_2\) vectores de dirección equivalentes:\( \vecs v=⟨6,−2,3⟩.\) Estas dos líneas son paralelas (ver la siguiente figura).

Ejercicio\( \PageIndex{4}\)

Describir la relación entre las líneas con las siguientes ecuaciones paramétricas:

\[ x=1−4t, \; y=3+t, \; z=8−6t \nonumber \]

\[x=2+3s,\; y=2s,\; z=−1−3s. \nonumber \]

Pista

Comience por identificar vectores de dirección para cada línea. ¿Uno es un múltiplo del otro?

Contestar

Estas líneas están sesgadas porque sus vectores de dirección no son paralelos y no hay ningún punto\( (x,y,z)\) que se encuentre en ambas líneas.

Ecuaciones para un Plano

Sabemos que una línea está determinada por dos puntos. En otras palabras, para dos puntos distintos, hay exactamente una línea que pasa por esos puntos, ya sea en dos dimensiones o en tres. De igual manera, dados tres puntos cualesquiera que no estén todos en la misma línea, hay un plano único que pasa por estos puntos. Así como una línea está determinada por dos puntos, un plano está determinado por tres.

Esta puede ser la forma más sencilla de caracterizar un plano, pero también podemos usar otras descripciones. Por ejemplo, dadas dos líneas distintas que se cruzan, hay exactamente un plano que contiene ambas líneas. Un plano también está determinado por una línea y cualquier punto que no se encuentre en la línea. Estas caracterizaciones surgen naturalmente de la idea de que un plano está determinado por tres puntos. Quizás la caracterización más sorprendente de un avión es en realidad la más útil.

Imagina un par de vectores ortogonales que comparten un punto inicial. Visualiza agarrando uno de los vectores y retorciéndolo. A medida que giras, el otro vector gira alrededor y barre un avión. Aquí, describimos ese concepto matemáticamente. Dejar\(\vecs{n}=⟨a,b,c⟩\) ser un vector y\(P=(x_0,y_0,z_0)\) ser un punto. Entonces el conjunto de todos los puntos\(Q=(x,y,z)\) tal que\(\vecd{PQ}\) es ortogonal\(\vecs{n}\) para formar un plano (Figura\(\PageIndex{7}\)). Decimos que\(\vecs{n}\) es un vector normal, o perpendicular al plano. Recuerde, el producto punto de vectores ortogonales es cero. Este hecho genera la ecuación vectorial de un plano:

\[\vecs{n}⋅\vecd{PQ}=0. \nonumber \]

Reescribir esta ecuación proporciona formas adicionales de describir el plano:

\[ \begin{align*} \vecs{n}⋅\vecd{PQ} &=0 \\[4pt] ⟨a,b,c⟩⋅⟨x−x_0,y−y_0,z−z_0⟩ &=0 \\[4pt] a(x−x_0)+b(y−y_0)+c(z−z_0) &=0. \end{align*}\]

Figura\(\PageIndex{7}\): Dado un punto\(P\) y un vector\(\vecs{n}\), el conjunto de todos los puntos\(Q\) con\(\vecd{PQ}\) ortogonal a\(\vecs{n}\) forma un plano.

Definición: Ecuación escalar de un plano

Dado un punto\(P\) y un vector\(\vecs n\), el conjunto de todos los puntos\(Q\) que satisfacen la ecuación\(\vecs n⋅\vecd{PQ}=0\) forma un plano. La ecuación

\[\vecs{n}⋅\vecd{PQ}=0 \nonumber \]

se conoce como la ecuación vectorial de un plano.

La ecuación escalar de un plano (a veces también llamada ecuación estándar de un plano) que contiene punto\(P=(x_0,y_0,z_0)\) con vector normal\(\vec{n}=⟨a,b,c⟩\) es

\[a(x−x_0)+b(y−y_0)+c(z−z_0)=0. \nonumber \]

Esta ecuación se puede expresar como\(ax+by+cz+d=0,\) donde\(d=−ax_0−by_0−cz_0.\) Esta forma de la ecuación a veces se llama la forma general de la ecuación de un plano.

Como se describió anteriormente en esta sección, cualquiera de los tres puntos que no se encuentran todos en la misma línea determinan un plano. Dados tres de esos puntos, podemos encontrar una ecuación para el plano que contiene estos puntos.

Ejemplo\(\PageIndex{5}\): Writing an Equation of a Plane Given Three Points in the Plane

Escribe una ecuación para el plano que contiene puntos\(P=(1,1,−2), Q=(0,2,1),\) y tanto\(R=(−1,−1,0)\) en forma estándar como general.

Solución

Para escribir una ecuación para un plano, debemos encontrar un vector normal para el plano. Comenzamos identificando dos vectores en el plano:

\[ \begin{align*} \vecd{PQ} &=⟨0−1,2−1,1−(−2)⟩\\[4pt] &=⟨−1,1,3⟩ \\[4pt] \vecd{QR} &=⟨−1−0,−1−2,0−1⟩\\[4pt] &=⟨−1,−3,−1⟩.\end{align*}\]

El producto cruzado\(\vecd{PQ}×\vecd{QR}\) es ortogonal a ambos\(\vecd{PQ}\) y\(\vecd{QR}\), por lo que es normal al plano que contiene estos dos vectores:

\[ \begin{align*} \vecs n &=\vecd{PQ}×\vecd{QR} \\[4pt] &=\begin{vmatrix}\mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k}\\−1 & 1 & 3\\−1 & −3 & −1\end{vmatrix} \\[4pt] &=(−1+9)\mathbf{\hat i}−(1+3)\mathbf{\hat j}+(3+1)\mathbf{\hat k} \\[4pt] &= 8\mathbf{\hat i}−4\mathbf{\hat j}+4\mathbf{\hat k}.\end{align*}\]

Así,\(\vecs n=⟨8,−4,4⟩,\) y podemos elegir cualquiera de los tres puntos dados para escribir una ecuación del plano:

\[ \begin{align*} 8(x−1)−4(y−1)+4(z+2) &=0 \\[4pt] 8x−4y+4z+4 &=0. \end{align*}\]

Las ecuaciones escalares de un plano varían según el vector normal y el punto elegido.

Ejemplo\(\PageIndex{6}\): Writing an Equation for a Plane Given a Point and a Line

Encuentra una ecuación del plano que pasa por el punto\((1,4,3)\) y contiene la línea dada por\(x=\dfrac{y−1}{2}=z+1.\)

Solución

Las ecuaciones simétricas describen la línea que pasa por el punto\((0,1,−1)\) paralelo al vector\(\vecs v_1=⟨1,2,1⟩\) (ver la siguiente figura). Utilice este punto y el punto dado,\((1,4,3),\) para identificar un segundo vector paralelo al plano:

\[ \vecs v_2=⟨1−0,4−1,3−(−1)⟩=⟨1,3,4⟩. \nonumber \]

Utilice el producto cruzado de estos vectores para identificar un vector normal para el plano:

\[ \begin{align*} \vecs n &=\vecs v_1×\vecs v_2 \nonumber \\[4pt] &=\begin{vmatrix}\mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k}\\1 & 2 & 1\\1 & 3 & 4\end{vmatrix} \nonumber \\[4pt] &=(8−3)\mathbf{\hat i}−(4−1)\mathbf{\hat j}+(3−2)\mathbf{\hat k} \\[4pt] &=5\mathbf{\hat i}−3\mathbf{\hat j}+\mathbf{\hat k}. \nonumber\end{align*}\]

Las ecuaciones escalares para el plano son\(5x−3(y−1)+(z+1)=0\) y\(5x−3y+z+4=0.\)

Ejercicio\(\PageIndex{6}\)

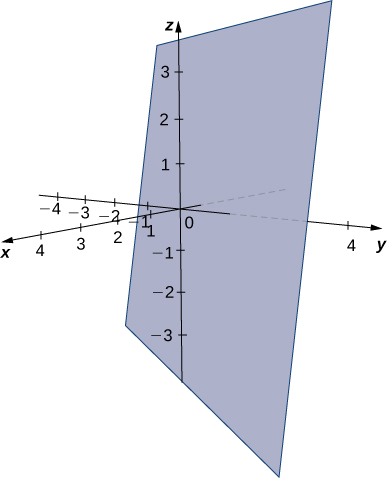
Encuentra una ecuación del plano que contiene las líneas\(L_1\) y\(L_2\):

\[ L_1: \; x=−y=z \nonumber \]

\[ L_2:\; \dfrac{x−3}{2}=y=z−2. \nonumber \]

Pista

Pista: El producto cruzado de los vectores de dirección de las líneas da un vector normal para el plano.

Contestar

\[ −2(x−1)+(y+1)+3(z−1)=0 \nonumber \]

o

\[ −2x+y+3z=0 \nonumber \]

Ahora que podemos escribir una ecuación para un plano, podemos usar la ecuación para encontrar la distancia\(d\) entre un punto\(P\) y el plano. Se define como la distancia más corta posible desde\(P\) hasta un punto en el plano.

Figura\(\PageIndex{8}\): Queremos encontrar la distancia más corta desde el punto P hasta el plano. Que punto\(R\) sea el punto en el plano tal que, para cualquier otro punto en el plano\(Q, ‖\vecd{RP}‖<‖\vecd{QP}‖\).

Así como encontramos la distancia bidimensional entre un punto y una línea calculando la longitud de un segmento de línea perpendicular a la línea, encontramos la distancia tridimensional entre un punto y un plano calculando la longitud de un segmento de línea perpendicular al plano. Dejar\(R\) ser el punto en el plano tal que\(\vecd{RP}\) sea ortogonal al plano, y dejar que\(Q\) sea un punto arbitrario en el plano. Después la proyección del vector\(\vecd{QP}\) sobre el vector normal describe vector\(\vecd{RP}\), como se muestra en la Figura\(\PageIndex{8}\).

La distancia entre un plano y un punto

Supongamos que un plano con vector normal\(\vecs{n}\) pasa a través del punto\(Q\). La distancia\(d\) desde el plano a un punto que\(P\) no está en el plano viene dada por

\[d=‖\text{proj}_\vecs{n}\,\vecd{QP}‖=∣\text{comp}_\vecs{n}\, \vecd{QP}∣=\dfrac{∣\vecd{QP}⋅\vecs{n}∣}{‖\vecs{n}‖}. \label{distanceplanepoint} \]

Ejemplo\(\PageIndex{7}\): Distance between a Point and a Plane

Encuentra la distancia entre punto\(P=(3,1,2)\) y plano dada por\(x−2y+z=5\) (ver la siguiente figura).

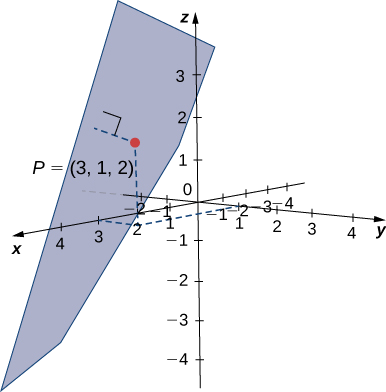
Solución

Los coeficientes de la ecuación del plano proporcionan un vector normal para el plano:\(\vecs{n}=⟨1,−2,1⟩\). Para encontrar vector\(\vecd{QP}\), necesitamos un punto en el plano. Cualquier punto va a funcionar, así que listo\(y=z=0\) para ver que ese punto\(Q=(5,0,0)\) se encuentra en el plano. Encuentra la forma componente del vector de\(Q\) a\(P\):

\[ \vecd{QP}=⟨3−5,1−0,2−0⟩=⟨−2,1,2⟩. \nonumber \]

Aplica la fórmula de distancia de la ecuación\ ref {distanceplanpoint}:

\[\begin{align*} d &=\dfrac{∣\vecd{QP}⋅\vecs n|}{‖\vecs n‖} \\[4pt] &=\dfrac{|⟨−2,1,2⟩⋅⟨1,−2,1⟩|}{\sqrt{1^2+(−2)^2+1^2}} \\[4pt] &=\dfrac{|−2−2+2|}{\sqrt{6}} \\[4pt] &=\dfrac{2}{\sqrt{6}} = \dfrac{\sqrt{6}}{3}\,\text{units}. \end{align*}\]

Ejercicio\(\PageIndex{7}\)

Encuentra la distancia entre punto\(P=(5,−1,0)\) y plano dada por\(4x+2y−z=3\).

Pista

Punto\((0,0,−3)\) yace en el avión.

Contestar

\[ \dfrac{15}{\sqrt{21}} = \dfrac{5\sqrt{21}}{7}\,\text{units} \nonumber \]

Planos paralelos e intersecantes

Hemos discutido las diversas relaciones posibles entre dos líneas en dos dimensiones y tres dimensiones. Cuando describimos la relación entre dos planos en el espacio, solo tenemos dos posibilidades: los dos planos distintos son paralelos o se cruzan. Cuando dos planos son paralelos, sus vectores normales son paralelos. Cuando dos planos se cruzan, la intersección es una línea (Figura\(\PageIndex{9}\)).

Figura\(\PageIndex{9}\): La intersección de dos planos no paralelos es siempre una línea.

Podemos usar las ecuaciones de los dos planos para encontrar ecuaciones paramétricas para la línea de intersección.

Ejemplo\(\PageIndex{8}\): Finding the Line of Intersection for Two Planes

Encuentra ecuaciones paramétricas y simétricas para la línea formada por la intersección de los planos dados por\(x+y+z=0\) y\(2x−y+z=0\) (ver la siguiente figura).

Solución

Tenga en cuenta que los dos planos tienen normales no paralelas, por lo que los planos se cruzan. Además, el origen satisface cada ecuación, por lo que sabemos que la línea de intersección pasa por el origen. Sumamos las ecuaciones de plano para que podamos eliminar una de las variables, en este caso,\(y\):

\(x+y+z=0\)

\(2x−y+z=0\)

________________

\(3x+2z=0\).

Esto nos da\(x=−\dfrac{2}{3}z.\) Sustituimos este valor en la primera ecuación para expresarlo\(y\) en términos de\(z\):

\[ \begin{align*} x+y+z =0 \\[4pt] −\dfrac{2}{3}z+y+z =0 \\[4pt] y+\dfrac{1}{3}z =0 \\[4pt] y =−\dfrac{1}{3}z \end{align*}. \nonumber \]

Ahora tenemos las dos primeras variables,\(x\) y\(y\), en términos de la tercera variable,\(z\). Ahora definimos\(z\) en términos de\(t\). Para eliminar la necesidad de fracciones, elegimos definir el parámetro\(t\) como\(t=−\dfrac{1}{3}z\). Entonces,\(z=−3t\). Sustituyendo la representación paramétrica de\(z\) back en las otras dos ecuaciones, vemos que las ecuaciones paramétricas para la línea de intersección son\(x=2t, \; y=t, \; z=−3t.\) Las ecuaciones simétricas para la línea son\(\dfrac{x}{2}=y=\dfrac{z}{−3}\).

Ejercicio\(\PageIndex{8}\)

Encuentra ecuaciones paramétricas para la línea formada por la intersección de planos\(x+y−z=3\) y\(3x−y+3z=5.\)

Pista

Sumar las dos ecuaciones, luego expresar\(z\) en términos de\(x\). Entonces, expresar\(y\) en términos de\(x\).

Contestar

\( x=t, \; y=7−3t,\; z=4−2t\)

Además de encontrar la ecuación de la línea de intersección entre dos planos, es posible que necesitemos encontrar el ángulo formado por la intersección de dos planos. Por ejemplo, los constructores que construyen una casa necesitan conocer el ángulo donde se encuentran diferentes secciones de la cubierta para saber si el techo se verá bien y drenará correctamente. Podemos usar vectores normales para calcular el ángulo entre los dos planos. Podemos hacer esto porque el ángulo entre los vectores normales es el mismo que el ángulo entre los planos. La figura\(\PageIndex{10}\) muestra por qué esto es cierto.

Figura\(\PageIndex{10}\): El ángulo entre dos planos tiene la misma medida que el ángulo entre los vectores normales para los planos.

Podemos encontrar la medida del ángulo\(θ\) entre dos planos de intersección encontrando primero el coseno del ángulo, usando la siguiente ecuación:

\[\cos θ=\dfrac{|\vecs{n}_1⋅\vecs{n}_2|}{‖\vecs{n}_1‖‖\vecs{n}_2‖}. \nonumber \]

Entonces podemos usar el ángulo para determinar si dos planos son paralelos u ortogonales o si se cruzan en algún otro ángulo.

Ejemplo\(\PageIndex{9}\): Finding the Angle between Two Planes

Determine si cada par de planos es paralelo, ortogonal o ninguno. Si los planos se cruzan, pero no ortogonales, encuentra la medida del ángulo entre ellos. Dar la respuesta en radianes y redondear a dos decimales.

1. \(x+2y−z=8\)y\(2x+4y−2z=10\)
2. \(2x−3y+2z=3\)y\(6x+2y−3z=1\)
3. \(x+y+z=4\)y\(x−3y+5z=1\)

Solución:

1. Los vectores normales para estos planos son\(\vecs{n}_1=⟨1,2,−1⟩\) y\(\vecs{n}_2=⟨2,4,−2⟩.\) Estos dos vectores son múltiplos escalares entre sí. Los vectores normales son paralelos, por lo que los planos son paralelos.
2. Los vectores normales para estos planos son\(\vecs{n}_1=⟨2,−3,2⟩\) y\(\vecs{n}_2=⟨6,2,−3⟩\). Tomando el producto punto de estos vectores, tenemos\[\begin{align*} \vecs{n}_1⋅\vecs{n}_2 =⟨2,−3,2⟩⋅⟨6,2,−3⟩\\[4pt] =2(6)−3(2)+2(−3)=0.\end{align*} \nonumber \] Los vectores normales son ortogonales, por lo que los planos correspondientes también son ortogonales.
3. Los vectores normales para estos planos son\(\vecs n_1=⟨1,1,1⟩\) y\(\vecs n_2=⟨1,−3,5⟩\):\[\begin{align*} \cos θ &=\dfrac{|\vecs{n}_1⋅\vecs{n}_2|}{‖\vecs{n}_1‖‖\vecs{n}_2‖} \\[4pt] &=\dfrac{|⟨1,1,1⟩⋅⟨1,−3,5⟩|}{\sqrt{1^2+1^2+1^2}\sqrt{1^2+(−3)^2+5^2}} \\[4pt] &=\dfrac{3}{\sqrt{105}} \end{align*}\]
   Entonces\(\theta =\arccos {\frac{3}{\sqrt{105}}} \approx 1.27\) rad.
   Así, el ángulo entre los dos planos es de aproximadamente\(1.27\) rad, o aproximadamente\(73°\).

Ejercicio\(\PageIndex{9}\)

Encuentra la medida del ángulo entre planos\(x+y−z=3\) y\(3x−y+3z=5.\) Da la respuesta en radianes y redondear a dos decimales.

Pista

Usa los coeficientes de las variables en cada ecuación para encontrar un vector normal para cada plano.

Contestar

\( 1.44\, \text{rad} \)

Cuando encontremos que dos planos son paralelos, es posible que necesitemos encontrar la distancia entre ellos. Para encontrar esta distancia, simplemente seleccionamos un punto en uno de los planos. La distancia de este punto al otro plano es la distancia entre los planos.

Anteriormente, introdujimos la fórmula para calcular esta distancia en la ecuación\ ref {distanceplanepoint}:

\[d=\dfrac{\vecd{QP}⋅\vecs{n}}{‖\vecs{n}‖}, \nonumber \]

donde\(Q\) es un punto en el plano,\(P\) es un punto no en el plano, y\(\vec{n}\) es el vector normal que pasa por el punto\(Q\). Considera la distancia de punto\((x_0,y_0,z_0)\) a plano\(ax+by+cz+k=0.\) Let\((x_1,y_1,z_1)\) ser cualquier punto en el plano. Sustituir en la fórmula rinde

\[\begin{align*}d =\dfrac{|a(x_0−x_1)+b(y_0−y_1)+c(z_0−z_1)|}{\sqrt{a^2+b^2+c^2}} \\[4pt] =\dfrac{|ax_0+by_0+cz_0+k|}{\sqrt{a^2+b^2+c^2}}.\end{align*}\]

Este resultado se expone formalmente en el siguiente teorema.

Distancia de un punto a un plano

Déjese\(P(x_0,y_0,z_0)\) ser un punto. La distancia desde\(P\) el plano\(ax+by+cz+k=0\) viene dada por

\[d=\dfrac{|ax_0+by_0+cz_0+k|}{\sqrt{a^2+b^2+c^2}}. \nonumber \]

Ejemplo\(\PageIndex{10}\): Finding the Distance between Parallel Planes

Encuentra la distancia entre los dos planos paralelos dada por\(2x+y−z=2\) y\(2x+y−z=8.\)

Solución

\((1,0,0)\)El punto se encuentra en el primer plano. La distancia deseada, entonces, es

\[\begin{align*} d &=\dfrac{|ax_0+by_0+cz_0+k|}{\sqrt{a^2+b^2+c^2}} \\[4pt] &= \dfrac{|2(1)+1(0)+(−1)(0)+(−8)|}{\sqrt{2^2+1^2+(−1)^2}} \\[4pt] &= \dfrac{6}{\sqrt{6}}=\sqrt{6} \,\text{units} \end{align*}\]

Ejercicio\(\PageIndex{10}\):

Encuentra la distancia entre planos paralelos\(5x−2y+z=6\) y\(5x−2y+z=−3\).

Pista

Establecer\(x=y=0\) para encontrar un punto en el primer plano.

Contestar

\(\dfrac{9}{\sqrt{30}} = \dfrac{3\sqrt{30}}{10}\,\text{units} \)

Distancia entre dos líneas oblicuas

Encontrar la distancia de un punto a una línea o de una línea a un plano parece un procedimiento bastante abstracto. Pero, si las líneas representan tuberías en una planta química o tubos en una refinería de petróleo o carreteras en una intersección de carreteras, confirmar que la distancia entre ellas cumple con las especificaciones puede ser importante y difícil de medir. Una forma es modelar las dos tuberías como líneas, utilizando las técnicas de este capítulo, para luego calcular la distancia entre ellas. El cálculo implica formar vectores a lo largo de las direcciones de las líneas y usar tanto el producto cruzado como el producto de punto.

Figura\(\PageIndex{11}\): Las instalaciones de tuberías industriales a menudo cuentan con tuberías que corren en diferentes direcciones. ¿Cómo podemos encontrar la distancia entre dos tubos sesgados?

Las formas simétricas de dos líneas,\(L_1\) y\(L_2\), son

\[L_1:\dfrac{x−x_1}{a_1}=\dfrac{y−y_1}{b_1}=\dfrac{z−z_1}{c_1} \nonumber \]

\[L_2:\dfrac{x−x_2}{a_2}=\dfrac{y−y_2}{b_2}=\dfrac{z−z_2}{c_2}. \nonumber \]

Se va a desarrollar una fórmula para la distancia\(d\) entre estas dos líneas, en términos de los valores\(a_1,b_1,c_1;a_2,b_2,c_2;x_1,y_1,z_1;\) y\(x_2,y_2,z_2.\) La distancia entre dos líneas suele tomarse para significar la distancia mínima, por lo que esta es la longitud de un segmento de línea o la longitud de un vector que es perpendicular a ambas líneas e intersecta ambas líneas.

1. Primero, anote dos vectores,\(\vecs{v}_1\) y\(\vecs{v}_2\), que se encuentran a lo largo\(L_1\) y\(L_2\), respectivamente.

2. Encuentra el producto cruzado de estos dos vectores y llámalo\(\vecs{N}\). Este vector es perpendicular a\(\vecs{v}_1\) y\(\vecs{v}_2\), y por lo tanto es perpendicular a ambas líneas.

3. A partir del vector\(\vecs{N}\), formar un vector unitario\(\vecs{n}\) en la misma dirección.

4. Utilice ecuaciones simétricas para encontrar un vector conveniente\(\vecs{v}_{12}\) que se encuentre entre dos puntos cualesquiera, uno en cada línea. Nuevamente, esto se puede hacer directamente desde las ecuaciones simétricas.

5. El producto punto de dos vectores es la magnitud de la proyección de un vector sobre el otro, es decir,\(\vecs A⋅\vecs B=‖\vecs{A}‖‖\vecs{B}‖\cos θ,\) dónde\(θ\) está el ángulo entre los vectores. Usando el producto punto, encuentre la proyección del vector\(\vecs{v}_{12}\) que se encuentra en paso\(4\) sobre el vector unitario\(\vecs{n}\) encontrado en el paso\(3\). Esta proyección es perpendicular a ambas líneas, y por lo tanto su longitud debe ser la distancia perpendicular d entre ellas. Tenga en cuenta que el valor de\(d\) puede ser negativo, dependiendo de su elección de vector\(\vecs{v}_{12}\) o el orden del producto cruzado, así que use signos de valor absoluto alrededor del numerador.

6. Comprueba que tu fórmula da la distancia correcta\(|−25|/\sqrt{198}≈1.78\) entre las dos líneas siguientes:

\[L_1:\dfrac{x−5}{2}=\dfrac{y−3}{4}=\dfrac{z−1}{3} \nonumber \]

\[L_2:\dfrac{x−6}{3}=\dfrac{y−1}{5}=\dfrac{z}{7}. \nonumber \]

7. ¿Su expresión general es válida cuando las líneas son paralelas? Si no, ¿por qué no? (Pista: ¿Qué sabe del valor del producto cruzado de dos vectores paralelos? ¿Para dónde aparecería ese resultado en tu expresión\(d\)?)

8. Demuestre que su expresión para la distancia es cero cuando las líneas se cruzan. Recordemos que dos líneas se cruzan si no son paralelas y están en el mismo plano. De ahí, considerar la dirección de\(\vecs{n}\) y\(\vecs{v}_{12}\). ¿Cuál es el resultado de su producto punto?

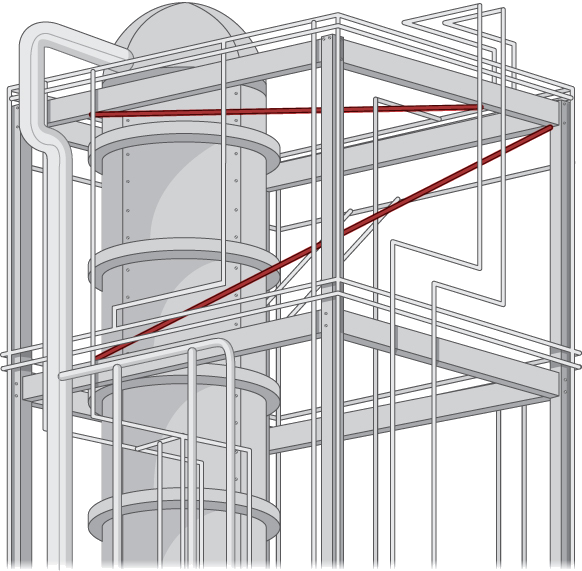
9. Considera la siguiente aplicación. Los ingenieros de una refinería han determinado que necesitan instalar puntales de soporte entre muchas de las tuberías de gas para reducir las vibraciones dañinas. Para minimizar el costo, planean instalar estos puntales en los puntos más cercanos entre tuberías sesgadas adyacentes. Debido a que tienen esquemas detallados de la estructura, son capaces de determinar las longitudes correctas de los puntales necesarios, y por lo tanto fabricarlos y distribuirlos a los equipos de instalación sin gastar un tiempo valioso haciendo mediciones.

La estructura de marco rectangular tiene las dimensiones\(4.0×15.0×10.0\,\text{m}\) (alto, ancho y profundidad). Un sector tiene una tubería que entra en la esquina inferior de la unidad de marco estándar y sale en la esquina diametralmente opuesta (la que está más alejada en la parte superior); llame a esto\(L_1\). Una segunda tubería entra y sale por las dos esquinas inferiores opuestas diferentes; llame a esto\(L_2\) (Figura\(\PageIndex{12}\)).

Figura\(\PageIndex{12}\): Dos tubos atraviesan una unidad de marco estándar.

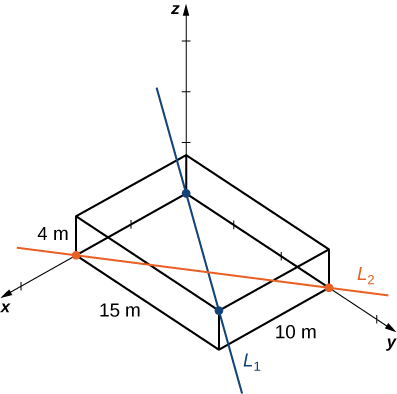
Anota los vectores a lo largo de las líneas que representan esas tuberías, encuentra el producto cruzado entre ellas a partir del cual crear el vector unitario\(\vecs n\), definir un vector que abarque dos puntos en cada línea, y finalmente determinar la distancia mínima entre las líneas. (Tome el origen para estar en la esquina inferior de la primera tubería.) Del mismo modo, también puede desarrollar las ecuaciones simétricas para cada línea y sustituirlas directamente en su fórmula.

Conceptos clave

• En tres dimensiones, la dirección de una línea se describe mediante un vector de dirección. La ecuación vectorial de una línea con vector de dirección\(\vecs v=⟨a,b,c⟩\) que pasa a través del punto\(P=(x_0,y_0,z_0)\) es\(\vecs r=\vecs r_0+t\vecs v\), donde\(\vecs r_0=⟨x_0,y_0,z_0⟩\) está el vector de posición del punto\(P\). Esta ecuación se puede reescribir para formar las ecuaciones paramétricas de la línea:\(x=x_0+ta,y=y_0+tb\), y\(z=z_0+tc\). La línea también se puede describir con las ecuaciones simétricas\(\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}\).
• Dejar\(L\) ser una línea en el espacio que pasa por punto\(P\) con vector de dirección\(\vecs v\). Si algún punto no\(Q\) está encendido\(L\), entonces la distancia de\(Q\) a\(L\) es\(d=\dfrac{‖\vecd{PQ}×\vecs v‖}{‖\vecs v‖}.\)
• En tres dimensiones, dos líneas pueden ser paralelas pero no iguales, iguales, intersecantes o sesgadas.
• Dado un punto\(P\) y un vector\(\vecs n\), el conjunto de todos los puntos que\(Q\) satisfacen la ecuación\(\vecs n⋅\vecd{PQ}=0\) forma un plano. \(\vecs n⋅\vecd{PQ}=0\)La ecuación se conoce como la ecuación vectorial de un plano.
• La ecuación escalar de un plano que contiene punto\(P=(x_0,y_0,z_0)\) con vector normal\(\vecs n=⟨a,b,c⟩\) es\(a(x−x_0)+b(y−y_0)+c(z−z_0)=0\). Esta ecuación se puede expresar como\(ax+by+cz+d=0,\) donde\(d=−ax_0−by_0−cz_0.\) Esta forma de la ecuación a veces se llama la forma general de la ecuación de un plano.
• Supongamos que un plano con vector normal\(n\) pasa a través del punto\(Q\). La distancia\(D\) desde el plano hasta el punto que\(P\) no está en el plano viene dada por

\[D=‖\text{proj}_\vecs{n}\vecd{QP}‖=∣\text{comp}_\vecs{n}\vec{QP}∣=\dfrac{∣\vec{QP}⋅\vecs n∣}{‖\vecs n‖.} \nonumber \]

• Los vectores normales de planos paralelos son paralelos. Cuando dos planos se cruzan, forman una línea.
• La medida del ángulo\(θ\) entre dos planos de intersección se puede encontrar usando la ecuación:\(\cos θ=\dfrac{|\vecs{n}_1⋅\vecs n_2|}{‖\vecs n_1‖‖\vecs n_2‖}\), donde\(\vecs n_1\) y\(\vecs n_2\) son vectores normales a los planos.
• La distancia\(D\) de punto\((x_0,y_0,z_0)\) a plano\(ax+by+cz+d=0\) viene dada por

\[D=\dfrac{|a(x_0−x_1)+b(y_0−y_1)+c(z_0−z_1)|} {\sqrt{a^2+b^2+c^2}}=\dfrac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}} \nonumber \].

Ecuaciones Clave

• Ecuación vectorial de una línea

\(\vecs r=\vecs r_0+t\vecs v\)

• Ecuaciones paramétricas de una línea

\(x=x_0+ta,\; y=y_0+tb,\)y\(z=z_0+tc\)

• Ecuaciones simétricas de una línea

\(\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}\)

• Ecuación vectorial de un plano

\(\vecs n⋅\vecd{PQ}=0\)

• Ecuación escalar de un plano

\(a(x−x_0)+b(y−y_0)+c(z−z_0)=0\)

• Distancia entre un Plano y un Punto

\(d=‖\text{proj}_\vecs{n}\vecd{QP}‖=∣\text{comp}_\vecs{n}\vecd{QP}∣=\dfrac{∣\vecd{QP}⋅\vecs n∣}{‖\vecs n‖}\)

Glosario

vector de dirección

un vector paralelo a una línea que se utiliza para describir la dirección u orientación de la línea en el espacio

forma general de la ecuación de un plano

una ecuación en la forma\(ax+by+cz+d=0,\) donde\(\vecs n=⟨a,b,c⟩\) es un vector normal del plano,\(P=(x_0,y_0,z_0)\) es un punto en el plano, y\(d=−ax_0−by_0−cz_0\)

vector normal

un vector perpendicular a un plano

ecuaciones paramétricas de una línea

el conjunto de ecuaciones\(x=x_0+ta, y=y_0+tb,\) y la\(z=z_0+tc\) descripción de la línea con vector de dirección\(v=⟨a,b,c⟩\) que pasa a través del punto\((x_0,y_0,z_0)\)

ecuación escalar de un plano

la ecuación\(a(x−x_0)+b(y−y_0)+c(z−z_0)=0\) utilizada para describir un plano que contiene punto\(P=(x_0,y_0,z_0)\) con vector normal\(n=⟨a,b,c⟩\) o su forma alternativa\(ax+by+cz+d=0\), donde\(d=−ax_0−by_0−cz_0\)

líneas sesgadas

dos líneas que no son paralelas pero no se cruzan

ecuaciones simétricas de una línea

las ecuaciones\(\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}\) que describen la línea con vector de dirección\(v=⟨a,b,c⟩\) que pasa a través del punto\((x_0,y_0,z_0)\)

ecuación vectorial de una línea

la ecuación\(\vecs r=\vecs r_0+t\vecs v\) utilizada para describir una línea con vector de dirección\(\vecs v=⟨a,b,c⟩\) que pasa a través del punto\(P=(x_0,y_0,z_0)\), donde\(\vecs r_0=⟨x_0,y_0,z_0⟩\), es el vector de posición del punto\(P\)

ecuación vectorial de un plano

la ecuación\(\vecs n⋅\vecd{PQ}=0,\) donde\(P\) es un punto dado en el plano,\(Q\) es cualquier punto en el plano, y\(\vecs n\) es un vector normal del plano