12.5E: Ejercicios para la Sección 12.5

Última actualización
Guardar como PDF

Page ID: 116145

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En los ejercicios 1 - 4,$ Q$ se dan puntos$ P$ y. Dejar$ L$ ser la línea que pasa por puntos$ P$ y$ Q$.

a. Encuentra la ecuación vectorial de la línea$ L$.

b. Encontrar ecuaciones paramétricas de línea$ L$.

c. Encuentra ecuaciones simétricas de línea$ L$.

d. Encontrar ecuaciones paramétricas del segmento de línea determinadas por$ P$ y$ Q$.

1)$ P(−3,5,9), \quad Q(4,−7,2)$

Responder: a.$\vecs r=⟨−3,5,9⟩+t⟨7,−12,−7⟩, \quad t∈R;$
b.$ x=−3+7t, \quad y=5−12t, \quad z=9−7t, \quad t∈R;$
c.$\dfrac{x+3}{7}=\dfrac{y−5}{−12}=\dfrac{z−9}{−7};$
d.$x=−3+7t, \quad y=5−12t, \quad z=9−7t, \quad 0 \le t \le 1$

2)$ P(4,0,5), \quad Q(2,3,1)$

3)$ P(−1,0,5), \quad Q(4,0,3)$

Responder: a.$\vecs r=⟨−1,0,5⟩+t⟨5,0,−2⟩, \quad t∈R;$
b.$ x=−1+5t,y=0,z=5−2t, \quad t∈R;$
c.$\dfrac{x+1}{5}=\dfrac{z−5}{−2}, \quad y=0;$
d.$x=−1+5t, \quad y=0, \quad z=5−2t, \quad t∈[0,1]$

4)$ P(7,−2,6), \quad Q(−3,0,6)$

Para los ejercicios 5 - 8,$\vecs v$ se dan punto$ P$ y vector. Dejar$ L$ ser la línea que pasa por el punto$ P$ con dirección$\vecs v$.

a. Encuentra ecuaciones paramétricas de línea$ L$.

b. Encontrar ecuaciones simétricas de línea$ L$.

c. Encuentra la intersección de la línea con el$xy$ plano.

5)$ P(1,−2,3),\,\vecs v=⟨1,2,3⟩$

Responder: a.$x=1+t, \quad y=−2+2t, \quad z=3+3t, \quad t∈R;$
b.$ \dfrac{x−1}{1}=\dfrac{y+2}{2}=\dfrac{z−3}{3};$
c.$(0,−4,0)$

6)$ P(3,1,5), \,\vecs v=⟨1,1,1⟩$

7)$ P(3,1,5), \,\vecs v=\vecd{QR},$ dónde$ Q(2,2,3)$ y$ R(3,2,3)$

Responder: a.$x=3+t, \quad y=1, \quad z=5, \quad t∈R;$
b.$ y=1, \quad z=5;$
c. La línea no se cruza con el$xy$ plano.

8)$ P(2,3,0), \,\vecs v=\vecd{QR},$ dónde$ Q(0,4,5)$ y$ R(0,4,6)$

Para los ejercicios 9 y 10,$ L$ se da línea.

a. Encontrar un punto$ P$ que pertenezca a la línea y un vector$\vecs v$ de dirección de la línea. Expresar$\vecs v$ en forma de componentes.

b. Encuentra la distancia desde el origen hasta la línea$ L$.

9)$ x=1+t, \quad y=3+t, \quad z=5+4t, \quad t∈R$

Responder: a. Un posible vector de punto y dirección son$P(1,3,5)$ y$\vecs v=⟨1,1,4⟩$, pero estas respuestas no son únicas.
b.$ \sqrt{3} $ unidades

10)$ −x=y+1, \quad z=2$

11) Encontrar la distancia entre el punto$ A(−3,1,1)$ y la línea de ecuaciones simétricas

$ x=−y=−z.$

Responder: $ \frac{2\sqrt{2}}{\sqrt{3}} = \frac{2\sqrt{6}}{3} $unidades

12) Encontrar la distancia entre el punto$ A(4,2,5)$ y la línea de ecuaciones paramétricas

$ x=−1−t, \; y=−t, \; z=2, \; t∈R.$

Para los ejercicios 13 - 14,$ L_2$ se dan líneas$ L_1$ y.

a. Verificar si las líneas$ L_1$ y$ L_2$ son paralelas.

b. Si las líneas$ L_1$ y$ L_2$ son paralelas, entonces encuentra la distancia entre ellas.

13)$ L_1:x=1+t, \quad y=t, \quad z=2+t, \quad t∈R$ y$L_2:x−3=y−1=z−3$

Responder: a. Paralelo;
b.$ \frac{\sqrt{2}}{\sqrt{3}} = \frac{\sqrt{6}}{3} $ unidades

14)$ L_1:x=2, \quad y=1, \quad z=t, \quad t∈R$ y$ L_2:x=1, \quad y=1, \quad z=2−3t, \quad t∈R$

15) Mostrar que la línea que pasa por puntos$ P(3,1,0)$ y$ Q(1,4,−3)$ es perpendicular a la línea con ecuación$ x=3t, \quad y=-32+8t, \quad z=−9+6t, \quad t∈R.$

Responder: $ \vecd{PQ} = \langle -2, 3, -3 \rangle$es el vector de dirección de la línea a través de puntos$P$ y$Q$, y el vector de dirección de la línea definida por las ecuaciones paramétricas anteriores es$\vecs v = \langle 3, 8, 6 \rangle.$
Since$\vecs v \cdot \vecd{PQ} = -6 + 24 - 18 = 0$, los dos vectores de dirección son ortogonales.
Ahora todo lo que necesitamos mostrar es que las dos líneas se cruzan.
La línea a través de puntos$ P(3,1,0)$ y$ Q(1,4,−3)$ tiene ecuaciones paramétricas:$x = 3 - 2u$,$y = 1 + 3u$, y$z = -3u$.
Estableciendo las$z$ coordenadas$x$ - y -de las dos líneas iguales, obtenemos el sistema de ecuaciones:
\[3t = 3 - 2u \quad\text{and}\quad -9 + 6t = -3u \nonumber \]
Resolver este sistema usando la sustitución nos da,$u = -3$ y$t = 3$. Tapar estos valores de$t$ y$u$ volver a las ecuaciones paramétricas de estas dos líneas nos da el punto de intersección con coordenadas$\left(9, -8, 9\right)$ en ambas líneas.
Por lo tanto, las líneas se cruzan y la línea a través de puntos$P$ y$Q$ con vector de dirección$\vecd{PQ} $ es perpendicular a la otra línea.

16) ¿Son las líneas de ecuaciones$ x=−2+2t, \quad y=−6, \quad z=2+6t, \quad t∈R$ y$ x=−1+t, \quad y=1+t, \quad z=t, \quad t∈R,$ perpendiculares entre sí?

17) Encontrar el punto de intersección de las líneas de ecuaciones$ x=−2y=3z$ y$ x=−5−t, \quad y=−1+t, \quad z=t−11, \quad t∈R.$

Responder: $ (−12,6,−4)$

18) Encontrar el punto de intersección del$x$ eje -con la línea de ecuaciones paramétricas$ x=10+t, \quad y=2−2t, \quad z=−3+3t, \quad t∈R.$

Para los ejercicios 19 - 22,$ L_2$ se dan líneas$ L_1$ y. Determine si las líneas son iguales, paralelas pero no iguales, sesgadas o intersecantes.

19)$ L_1:x=y−1=−z$ y$ L_2:x−2=−y=\dfrac{z}{2}$

Responder: Las líneas están sesgadas.

20)$ L_1:x=2t, \quad y=0, \quad z=3, \quad t∈R$ y$ L_2:x=0, \quad y=8+s, \quad z=7+s, \quad s∈R$

21)$ L_1:x=−1+2t, \quad y=1+3t, \quad z=7t, \quad t∈R$ y$ L_2:x−1=\frac{2}{3}(y−4)=\frac{2}{7}z−2$

Responder: Las líneas son iguales.

22)$ L_1:3x=y+1=2z$ y$ L_2:x=6+2t, \quad y=17+6t, \quad z=9+3t, \quad t∈R$

23) Considerar$ L$ la línea de ecuaciones simétricas$ x−2=−y=\dfrac{z}{2}$ y punto$ A(1,1,1).$

a. Encuentra ecuaciones paramétricas para una línea paralela a la$ L$ que pasa por el punto$ A$.

b. Encontrar ecuaciones simétricas de una línea sesgada hacia$ L$ y que pasa a través del punto$ A$.

c. Encuentra ecuaciones simétricas de una línea que se cruza$ L$ y pasa a través del punto$ A$.

Responder: a.$x=1+t, \quad y=1−t, \quad z=1+2t, \quad t∈R$
b. Por ejemplo, la línea que pasa$ A$ con el vector de dirección$ j:x=1,z=1$
c. Por ejemplo, la línea que pasa a través$ A$ y el punto$ (2,0,0)$ que pertenece$ L$ es una línea que se cruza;$ L:\frac{x−1}{−1}=y−1=z−1$

24) Considerar la línea$ L$ de ecuaciones paramétricas$ x=t, \quad y=2t, \quad z=3, \quad t∈R.$

a. Encuentra ecuaciones paramétricas para una línea paralela a la$ L$ que pasa por el origen.

b. Encontrar ecuaciones paramétricas de una línea sesgada a$ L$ que pasa por el origen.

c. Encontrar ecuaciones simétricas de una línea que se cruza$ L$ y pasa por el origen.

Para los ejercicios 25 - 28,$\vecs n$ se dan punto$ P$ y vector.

a. Encuentra la ecuación escalar del plano que atraviesa$ P$ y tiene vector normal$\vecs n$.

b. encontrar la forma general de la ecuación del plano que atraviesa$ P$ y tiene vector normal$\vecs n$.

25)$ P(0,0,0), \quad \vecs n=3\mathbf{\hat i}−2\mathbf{\hat j}+4\mathbf{\hat k}$

Responder: a.$3x−2y+4z=0$
b.$3x−2y+4z=0$

26)$ P(3,2,2), \quad \vecs n=2\mathbf{\hat i}+3\mathbf{\hat j}−\mathbf{\hat k}$

27)$ P(1,2,3), \quad \vecs n=⟨1,2,3⟩$

Responder: a.$(x−1)+2(y−2)+3(z−3)=0$
b.$x+2y+3z−14=0$

28)$ P(0,0,0), \quad \vecs n=⟨−3,2,−1⟩$

Para los ejercicios 29 - 32, se da la ecuación de un plano.

a. Encontrar vector normal$\vecs n$ al plano. Expresar$\vecs n$ usando vectores unitarios estándar.

b. Encontrar las intersecciones del plano con cada uno de los ejes de coordenadas (sus intercepciones).

c. Esbozar el plano.

29) [T]$ 4x+5y+10z−20=0$

Responder

a.$\vecs n=4\mathbf{\hat i}+5\mathbf{\hat j}+10\mathbf{\hat k}$
b.$(5,0,0), \,(0,4,0),$ y$ (0,0,2)$

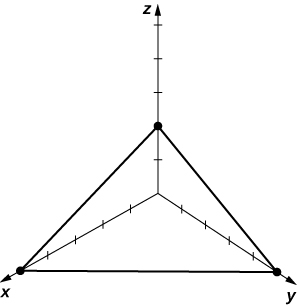
30)$ 3x+4y−12=0$

31)$ 3x−2y+4z=0$

Responder

a.$\vecs n=3\mathbf{\hat i}−2\mathbf{\hat j}+4\mathbf{\hat k}$
b.$(0,0,0)$

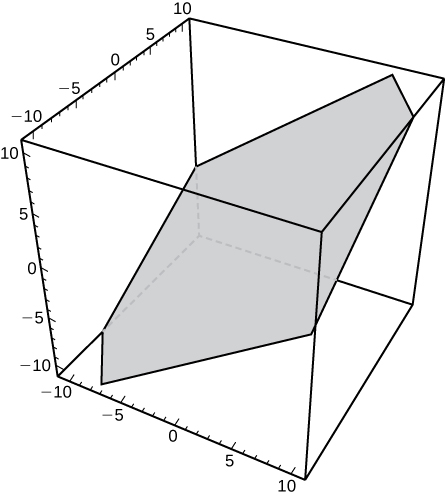
32)$ x+z=0$

33) Dado punto$ P(1,2,3)$ y vector$\vecs n=\mathbf{\hat i}+\mathbf{\hat j}$, encontrar punto$ Q$ en el$x$ eje -tal que$ \vecd{PQ}$ y$\vecs n$ son ortogonales.

Responder: $ (3,0,0)$

34) Mostrar que no hay plano perpendicular al$\vecs n=\mathbf{\hat i}+\mathbf{\hat j}$ que pasa por puntos$ P(1,2,3)$ y$ Q(2,3,4)$.

35) Encuentra ecuaciones paramétricas de la línea que pasa a través del punto$ P(−2,1,3)$ que es perpendicular al plano de ecuación$ 2x−3y+z=7.$

Responder: $ x=−2+2t, \quad y=1−3t, \quad z=3+t, \quad t∈R$

36) Encuentra ecuaciones simétricas de la línea que pasa a través del punto$ P(2,5,4)$ que es perpendicular al plano de ecuación$ 2x+3y−5z=0.$

37) Mostrar que la línea$ \dfrac{x−1}{2}=\dfrac{y+1}{3}=\dfrac{z−2}{4}$ es paralela al plano$ x−2y+z=6$.

38) Encontrar el número real de$ α$ tal manera que la línea de ecuaciones paramétricas$ x=t, \quad y=2−t, \quad z=3+t, \quad t∈R$ sea paralela al plano de ecuación$ αx+5y+z−10=0.$

Para los ejercicios 39 - 42, se dan las ecuaciones de dos planos.

a. Determinar si los planos son paralelos, ortogonales o ninguno.

b. Si los planos no son paralelos ni ortogonales, entonces encuentra la medida del ángulo entre los planos. Exprese la respuesta en grados redondeados al entero más cercano.

c. Si los planos se cruzan, busque la línea de intersección de los planos, proporcionando las ecuaciones paramétricas de esta línea.

39) [T]$ x+y+z=0, \quad 2x−y+z−7=0$

Responder: a. Los planos no son paralelos ni ortogonales.
b.$62°$
c.$x = -1 + 2t$
$y = -4 + t$
$z = 5 - 3t$

40)$ 5x−3y+z=4, \quad x+4y+7z=1$

41)$ x−5y−z=1, \quad 5x−25y−5z=−3$

Responder: a. Los planos son paralelos.

42) [T]$ x−3y+6z=4, \quad 5x+y−z=4$

Para los ejercicios 43 - 46, determine si la línea dada se cruza con el plano dado. Si se cruzan, indicar el punto de intersección.

43) Plano:$2x + y - z = 11$ Línea:$x = 1 + t, \quad y = 3 - 2t, \quad z = 2 +4t$

Responder: Se cruzan en el punto$ (-1, 7, -6) $.

44) Plano:$-x + 2y + z = 2$ Línea:$x = 1 + 2t, \quad y = -2 + t, \quad z = 5 - 3t$

Responder: Se cruzan en el punto$ \left(-\frac{1}{3}, \, -\frac{8}{3}, \, 7\right) $.

45) Plano:$x - 3y + 2z = 4$ Línea:$x = 2 - t, \quad y = t, \quad z = 4 +2t$

Responder: La línea no se intersecta con este plano.

46) Plano:$x - 3y + 2z = 10$ Línea:$x = 2 - t, \quad y = t, \quad z = 4 +2t$

Responder: La línea en realidad está completamente contenida en este plano, por lo que cada punto de la línea está en el plano. Por ejemplo, cuando$t = 0$ tenemos el punto,$(2, 0, 4)$.

47) Demostrar que las líneas de ecuaciones$ x=t, \quad y=1+t, \quad z=2+t, \quad t∈R,$ y$ \dfrac{x}{2}=\dfrac{y−1}{3}=z−3$ están sesgadas, y encontrar la distancia entre ellas.

Responder: $ \frac{1}{\sqrt{6}} = \frac{\sqrt{6}}{6}$unidades

48) Demostrar que las líneas de ecuaciones$ x=−1+t, \quad y=−2+t, \quad z=3t, \quad t∈R,$ y$ x=5+s, \quad y=−8+2s, \quad z=7s, \quad s∈R$ están sesgadas, y encontrar la distancia entre ellas.

49) Considerar el punto$ C(−3,2,4)$ y el plano de ecuación$ 2x+4y−3z=8$.

a. Encuentra el radio de la esfera con$C$ tangente central al plano dado.

b. Encontrar punto$P$ de tangencia.

Responder: a.$r = \frac{18}{\sqrt{29}} = \frac{18\sqrt{29}}{29}$
b.$P\left(−\frac{51}{29},\frac{130}{29},\frac{62}{29}\right)$

50) Considerar el plano de ecuación$ x−y−z−8=0.$

a. Encuentra la ecuación de la esfera con centro$C$ en el origen que es tangente al plano dado.

b. Encontrar ecuaciones paramétricas de la línea que pasa por el origen y el punto de tangencia.

51) Dos niños están jugando con una pelota. La chica le lanza la pelota al chico. La pelota viaja en el aire, se curva$ 3$ pies a la derecha y cae a$ 5$ pies de distancia de la niña (ver la siguiente figura). Si el plano que contiene la trayectoria de la pelota es perpendicular al suelo, encuentra su ecuación.

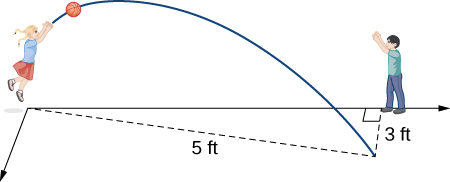
Responder: $ 4x−3y=0$

52) [T] John asigna$ d$ dólares para consumir mensualmente tres bienes de precios$ a,b$, y$ c$. En este contexto, la ecuación presupuestal se define como$ ax+by+cz=d,$ dónde$ x≥0,\, y≥0$, y$ z≥0$ representan el número de artículos comprados de cada una de las mercancías. El conjunto presupuestal viene dado por$ \big\{(x,y,z)\,|\,ax+by+cz≤d,\;x≥0,\;y≥0,\;z≥0\big\},$ y el plano presupuestal es la parte del plano de ecuación$ ax+by+cz=d$ para el cual$ x≥0,\,y≥0$, y$ z≥0$. Considerar$ a=$8, \,b=$5, \,c=$10,$ y$ d=$500.$

a. Utilice un CAS para graficar el conjunto de presupuestos y el plano presupuestal.

b. para$ z=25,$ encontrar la nueva ecuación presupuestal y graficar el presupuesto establecido en el mismo sistema de coordenadas.

53) [T] Considerar$\vecs r(t)=⟨\sin t,\cos t,2t⟩$ el vector de posición de una partícula en el momento$ t∈[0,3]$, donde los componentes de$\vecs r$ se expresan en centímetros y el tiempo se mide en segundos. Dejar$ \vecd{OP}$ ser el vector de posición de la partícula después de la$ 1$ sec.

a. Determinar el vector$\vecs v(1)$ de velocidad de la partícula después de la$ 1$ sec.

b. Encuentra la ecuación escalar del plano que es perpendicular al punto$ v(1)$ y pasa a través del mismo$ P$. Este plano se llama el plano normal a la trayectoria de la partícula en el punto$ P$.

c. Utilice un CAS para visualizar la trayectoria de la partícula junto con el vector de velocidad y el plano normal en el punto$ P$.

Responder: a.$\vecs v(1)=⟨\cos 1,−\sin 1, 2⟩$
b.$ (\cos 1)(x−\sin 1)−(\sin 1)(y−\cos 1)+2(z−2)=0$
c.

54) [T] Un panel solar está montado en el techo de una casa. El panel puede ser considerado como posicionado en los puntos de coordenadas (en metros)$ A(8,0,0), \, B(8,18,0), \, C(0,18,8),$ y$ D(0,0,8)$ (ver la siguiente figura).

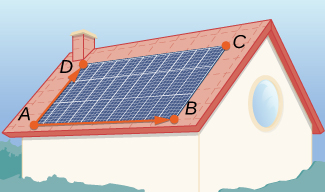
a. Encontrar la forma general de la ecuación del plano que contiene el panel solar mediante el uso de puntos$ A, \, B,$ y$ C$, y mostrar que su vector normal es equivalente a$ \vecd{AB}×\vecd{AD}.$

b. encontrar ecuaciones paramétricas de línea$ L_1$ que pasa por el centro del panel solar y tiene un vector de dirección$\vecs s=\frac{1}{\sqrt{3}}\mathbf{\hat i}+\frac{1}{\sqrt{3}}\mathbf{\hat j}+\frac{1}{\sqrt{3}}\mathbf{\hat k},$ que apunta hacia la posición del Sol a una hora determinada del día.

c. Encontrar ecuaciones simétricas de línea$ L_2$ que pasa por el centro del panel solar y es perpendicular a éste.

d. Determinar el ángulo de elevación del Sol sobre el panel solar mediante el uso del ángulo entre líneas$ L_1$ y$ L_2$.

Colaboradores

Template:ContribOpenStaxCalc

Problemas 15 y 43 - 46 creado por Paul Seeburger