Saltar al contenido principal
LibreTexts Español

12.6E: Ejercicios para la Sección 12.6

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    116144

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Para los ejercicios 1 - 6, esboce y describa la superficie cilíndrica de la ecuación dada.

    1) [T]\( x^2+z^2=1\)

    Contestar

    La superficie es un cilindro con las reglas paralelas al\(y\) eje -eje.

    2) [T]\( x^2+y^2=9\)

    3) [T]\( z=\cos\left(\frac{π}{2}+x\right)\)

    Contestar

    La superficie es un cilindro con reglas paralelas al\(y\) eje.

    4) [T]\( z=e^x\)

    5) [T]\( z=9−y^2\)

    Contestar

    La superficie es un cilindro con reglas paralelas al\(x\) eje.

    6) [T]\( z=\ln x\)

    Para los ejercicios 7 - 10, se da la gráfica de una superficie cuádrica.

    a. Especifique el nombre de la superficie cuádrica.

    b. Determinar el eje de simetría de la superficie cuádrica.

    7)

    Contestar
    a. Cilindro; b. El\(x\) eje

    8)

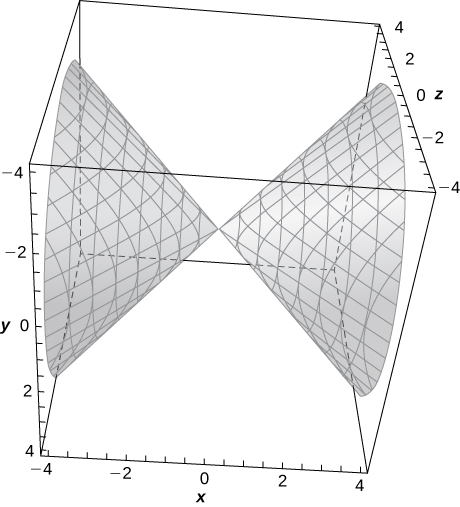
    9)

    Contestar
    a. Hiperboloide de dos hojas; b. El\(x\) eje

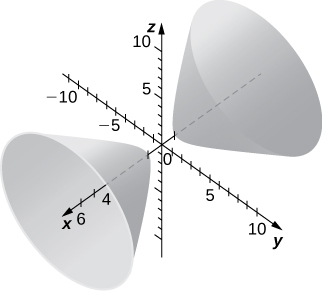
    10)

    Para los ejercicios 11 - 16, haga coincidir la superficie cuádrica dada con su ecuación correspondiente en forma estándar.

    a.\( \dfrac{x^2}{4}+\dfrac{y^2}{9}−\dfrac{z^2}{12}=1\)

    b.\( \dfrac{x^2}{4}−\dfrac{y^2}{9}−\dfrac{z^2}{12}=1\)

    c.\( \dfrac{x^2}{4}+\dfrac{y^2}{9}+\dfrac{z^2}{12}=1\)

    d.\( z^2=4x^2+3y^2\)

    e.\( z=4x^2−y^2\)

    f.\( 4x^2+y^2−z^2=0\)

    11) Hiperboloide de dos hojas

    Contestar
    b.

    12) Elipsoide

    13) paraboloide elíptico

    Contestar
    d.

    14) Paraboloide hiperbólico

    15) Hiperboloide de una hoja

    Contestar
    a.

    16) Cono elíptico

    Para los ejercicios 17 - 28, reescriba la ecuación dada de la superficie cuádrica en forma estándar. Identificar la superficie.

    17)\( −x^2+36y^2+36z^2=9\)

    Contestar
    \( −\dfrac{x^2}{9}+\dfrac{y^2}{\frac{1}{4}}+\dfrac{z^2}{\frac{1}{4}}=1,\)hiperboloide de una hoja con el\(x\) eje -eje como eje de simetría

    18)\( −4x^2+25y^2+z^2=100\)

    19)\( −3x^2+5y^2−z^2=10\)

    Contestar
    \( −\dfrac{x^2}{\frac{10}{3}}+\dfrac{y^2}{2}−\dfrac{z^2}{10}=1,\)hiperboloide de dos hojas con el\(y\) eje -como eje de simetría

    20)\( 3x^2−y^2−6z^2=18\)

    21)\( 5y=x^2−z^2\)

    Contestar
    \( y=−\dfrac{z^2}{5}+\dfrac{x^2}{5},\)paraboloide hiperbólico con el\(y\) eje -como eje de simetría

    22)\( 8x^2−5y^2−10z=0\)

    23)\( x^2+5y^2+3z^2−15=0\)

    Contestar
    \( \dfrac{x^2}{15}+\dfrac{y^2}{3}+\dfrac{z^2}{5}=1,\)elipsoide

    24)\( 63x^2+7y^2+9z^2−63=0\)

    25)\( x^2+5y^2−8z^2=0\)

    Contestar
    \( \dfrac{x^2}{40}+\dfrac{y^2}{8}−\dfrac{z^2}{5}=0,\)cono elíptico con el\(z\) eje -eje como su eje de simetría

    26)\( 5x^2−4y^2+20z^2=0\)

    27)\( 6x=3y^2+2z^2\)

    Contestar
    \( x=\dfrac{y^2}{2}+\dfrac{z^2}{3},\)paraboloide elíptico con el\(x\) eje -como eje de simetría

    28)\( 49y=x^2+7z^2\)

    Para los ejercicios 29 - 34, busque la traza de la superficie cuádrica dada en el plano de coordenadas especificado y bosquéela.

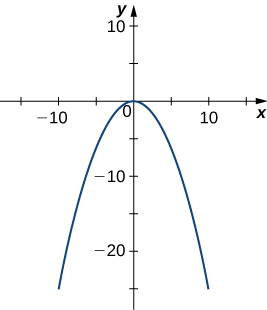
    29) [T]\( x^2+z^2+4y=0, \quad z=0\)

    Contestar

    Parábola\( y=−\frac{x^2}{4},\)

    30) [T]\( x^2+z^2+4y=0,\quad x=0\)

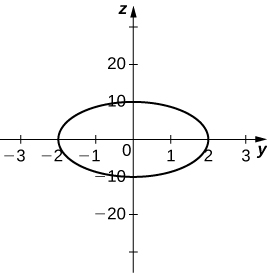
    31) [T]\( −4x^2+25y^2+z^2=100,\quad x=0\)

    Contestar

    Elipse\( \dfrac{y^2}{4}+\dfrac{z^2}{100}=1,\)

    32) [T]\( −4x^2+25y^2+z^2=100,\quad y=0\)

    33) [T]\( x^2+\dfrac{y^2}{4}+\dfrac{z^2}{100}=1,\quad x=0\)

    Contestar

    Elipse\( \dfrac{y^2}{4}+\dfrac{z^2}{100}=1,\)

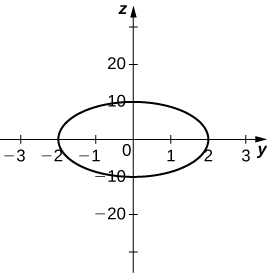
    34) [T]\( x^2−y−z^2=1,\quad y=0\)

    35) Utilice la gráfica de la superficie cuádrica dada para responder a las preguntas.

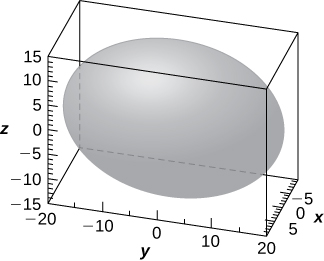
    a. Especifique el nombre de la superficie cuádrica.

    b. ¿Cuál de las ecuaciones\( 16x^2+9y^2+36z^2=3600, \; 9x^2+36y^2+16z^2=3600,\) —o\( 36x^2+9y^2+16z^2=3600\) —corresponde a la gráfica?

    c. Utilice b. para escribir la ecuación de la superficie cuádrica en forma estándar.

    Contestar
    a. Elipsoide
    b. La tercera ecuación
    c.\( \dfrac{x^2}{100}+\dfrac{y^2}{400}+\dfrac{z^2}{225}=1\)

    36) Utilizar la gráfica de la superficie cuádrica dada para responder a las preguntas.

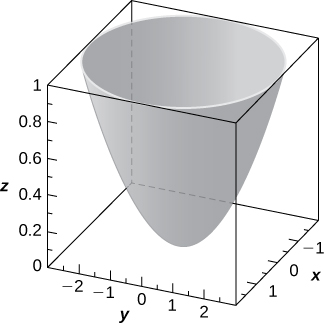
    a. Especifique el nombre de la superficie cuádrica.

    b. ¿Cuál de las ecuaciones—\( 36z=9x^2+y^2, \; 9x^2+4y^2=36z\), o\( −36z=−81x^2+4y^2\) —corresponde a la gráfica anterior?

    c. Utilice b. para escribir la ecuación de la superficie cuádrica en forma estándar.

    Para los ejercicios 37 - 42, se da la ecuación de una superficie cuádrica.

    a. Utilice el método de completar el cuadrado para escribir la ecuación en forma estándar.

    b. Identificar la superficie.

    37)\( x^2+2z^2+6x−8z+1=0\)

    Contestar
    a.\(\dfrac{(x+3)^2}{16}+\dfrac{(z−2)^2}{8}=1\)
    b. Cilindro centrado en\( (−3,2)\) con reglas paralelas al\(y\) eje

    38)\( 4x^2−y^2+z^2−8x+2y+2z+3=0\)

    39)\( x^2+4y^2−4z^2−6x−16y−16z+5=0\)

    Contestar
    a.\(\dfrac{(x−3)^2}{4}+(y−2)^2−(z+2)^2=1\)
    b. Hiperboloide de una hoja centrada\( (3,2,−2),\) con el\(z\) eje -como su eje de simetría

    40)\( x^2+z^2−4y+4=0\)

    41)\( x^2+\dfrac{y^2}{4}−\dfrac{z^2}{3}+6x+9=0\)

    Contestar
    a.\((x+3)^2+\dfrac{y^2}{4}−\dfrac{z^2}{3}=0\)
    b. Cono elíptico centrado en\( (−3,0,0),\) con el\(z\) eje -como su eje de simetría

    42)\( x^2−y^2+z^2−12z+2x+37=0\)

    43) Escribir la forma estándar de la ecuación del elipsoide centrada en el origen que pasa por puntos\( A(2,0,0),\, B(0,0,1),\) y\( C\left(12,\sqrt{11},\frac{1}{2}\right).\)

    Contestar
    \( \dfrac{x^2}{4}+\dfrac{y^2}{16}+z^2=1\)

    44) Escribir la forma estándar de la ecuación del elipsoide centrada en el punto\( P(1,1,0)\) que pasa por puntos\( A(6,1,0),\, B(4,2,0)\) y\( C(1,2,1)\).

    45) Determinar los puntos de intersección del cono elíptico\( x^2−y^2−z^2=0\) con la línea de ecuaciones simétricas\( \dfrac{x−1}{2}=\dfrac{y+1}{3}=z.\)

    Contestar
    \( (1,−1,0)\)y\( \left(\frac{13}{3},4,\frac{5}{3}\right)\)

    46) Determinar los puntos de intersección del hiperboloide parabólico\( z=3x^2−2y^2\) con la línea de ecuaciones paramétricas\( x=3t,\;y=2t,\;z=19t\), donde\( t∈R.\)

    47) Encuentra la ecuación de la superficie cuádrica con puntos\( P(x,y,z)\) que son equidistantes del punto\( Q(0,−1,0)\) y plano de ecuación\( y=1.\) Identificar la superficie.

    Contestar
    \( x^2+z^2+4y=0,\)paraboloide elíptico

    48) Encuentra la ecuación de la superficie cuádrica con puntos\( P(x,y,z)\) que son equidistantes del punto\( Q(0,2,0)\) y plano de ecuación\( y=−2.\) Identificar la superficie.

    49) Si la superficie de un reflector parabólico se describe por ecuación\( 400z=x^2+y^2,\) encontrar el punto focal del reflector.

    Contestar
    \( (0,0,100)\)

    50) Considerar el reflector parabólico descrito por la ecuación\( z=20x^2+20y^2.\) Encuentra su punto focal.

    51) Mostrar que la superficie cuádrica se\( x^2+y^2+z^2+2xy+2xz+2yz+x+y+z=0\) reduce a dos planos paralelos.

    52) Mostrar que la superficie cuádrica se\( x^2+y^2+z^2−2xy−2xz+2yz−1=0\) reduce a dos planos paralelos que pasan.

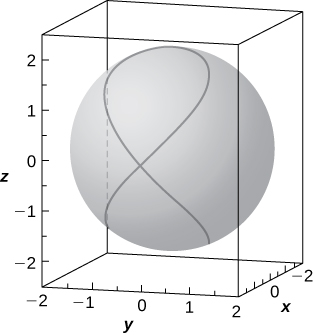
    53) [T] La intersección entre cilindro\( (x−1)^2+y^2=1\) y esfera\( x^2+y^2+z^2=4\) se denomina curva Viviani.

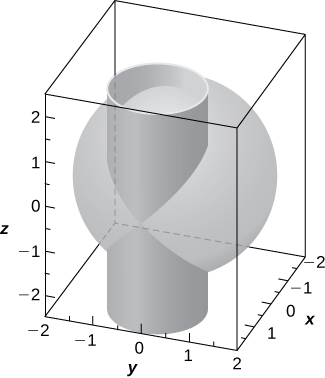
    a. Resolver el sistema que consiste en las ecuaciones de las superficies para encontrar la ecuación de la curva de intersección. (Pista: Encontrar\( x\) y\( y\) en términos de\( z\).)

    b. utilizar un sistema de álgebra computacional (CAS) o CalcPlot3D para visualizar la curva de intersección en la esfera\( x^2+y^2+z^2=4\).

    Contestar

    a.\(x=2−\dfrac{z^2}{2}, \quad y=±\dfrac{z}{2}\sqrt{4−z^2},\) donde\( z∈[−2,2];\)

    b.

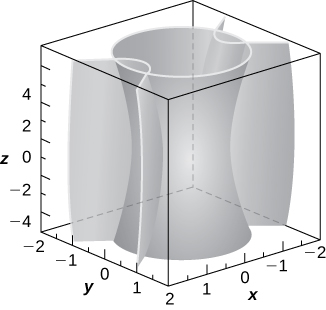
    54) El hiperboloide de una hoja\( 25x^2+25y^2−z^2=25\) y el cono elíptico\( −25x^2+75y^2+z^2=0\) se representan en la siguiente figura junto con sus curvas de intersección. Identificar las curvas de intersección y encontrar sus ecuaciones (Pista: Encuentra y del sistema que consiste en las ecuaciones de las superficies.)

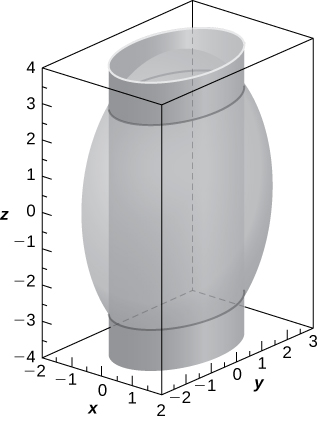
    55) [T] Utilice un CAS o CalcPlot3D para crear la intersección entre cilindro\( 9x^2+4y^2=18\) y elipsoide\( 36x^2+16y^2+9z^2=144\), y encontrar las ecuaciones de las curvas de intersección.

    Contestar

    dos elipses de ecuaciones\( \dfrac{x^2}{2}+\dfrac{y^2}{\frac{9}{2}}=1\) en planos\( z=±2\sqrt{2}\)

    56) [T] Un esferoide es un elipsoide con dos semiejes iguales. Por ejemplo, la ecuación de un esferoide con el eje z como eje de simetría viene dada por\( \dfrac{x^2}{a^2}+\dfrac{y^2}{a^2}+\dfrac{z^2}{c^2}=1\), donde\( a\) y\( c\) son números reales positivos. El esferoide se llama oblato si\( c<a\), y prolate para\( c>a\).

    a. La córnea del ojo se aproxima como un esferoide prolado con un eje que es el ojo, donde\( a=8.7mm\) y\( c=9.6mm\) .Escribe la ecuación del esferoide que modela la córnea y dibuja la superficie.

    b. Dar dos ejemplos de objetos con formas esferoides proladas.

    57) [T] En la cartografía, la Tierra es aproximada por un esferoide oblato más que por una esfera. Los radios en el ecuador y los polos son aproximadamente\( 3963\) mi y\( 3950\) mi, respectivamente.

    a. Escribir la ecuación en forma estándar del elipsoide que representa la forma de la Tierra. Supongamos que el centro de la Tierra está en el origen y que la traza formada por plano\( z=0\) corresponde al ecuador.

    b. Esbozar la gráfica.

    c. Encuentra la ecuación de la curva de intersección de la superficie con plano\( z=1000\) que es paralelo al\(xy\) plano. La curva de intersección se llama paralelo.

    d. Encuentra la ecuación de la curva de intersección de la superficie con plano\( x+y=0\) que pasa por el\(z\) eje. La curva de intersección se llama meridiano.

    Contestar

    a.\(\dfrac{x^2}{3963^2}+\dfrac{y^2}{3963^2}+\dfrac{z^2}{3950^2}=1\)

    b.

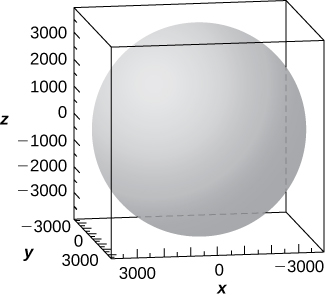
    c. La curva de intersección es la elipse de la ecuación\( \dfrac{x^2}{3963^2}+\dfrac{y^2}{3963^2}=\dfrac{(2950)(4950)}{3950^2}\), y la intersección es una elipse.
    d. La curva de intersección es la elipse de la ecuación\( \dfrac{2y^2}{3963^2}+\dfrac{z^2}{3950^2}=1.\)

    58) [T] Un conjunto de imanes de acrobacias zumbantes (o “huevos de serpiente de cascabel”) incluye dos imanes brillantes, pulidos y superfuertes en forma de esferoide conocidos por el entretenimiento infantil. Cada imán está\( 1.625\) en. largo y\( 0.5\) en. ancho en el medio. Mientras los arrojan al aire, crean un zumbido a medida que se atraen entre sí.

    a. escribir la ecuación del esferoide prolado centrado en el origen que describe la forma de uno de los imanes.

    b. escribir las ecuaciones de los esferoides prolados que modelan la forma de los imanes de acrobacias zumbantes. Utilice un CAS o CalcPlot3D para crear las gráficas.

    59) [T] Una superficie en forma de corazón viene dada por la ecuación\( (x^2+\frac{9}{4}y^2+z^2−1)^3−x^2z^3−\frac{9}{80}y^2z^3=0.\)

    a. Utilice un CAS o CalcPlot3D para graficar la superficie que modela esta forma.

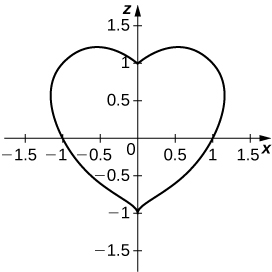
    b. Determinar y esbozar el rastro de la superficie en forma de corazón en el\(xz\) plano.

    Contestar

    a.

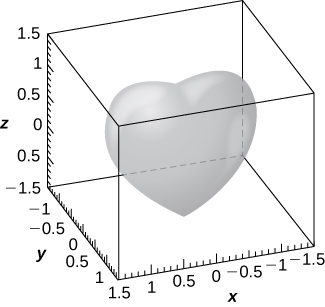
    b. La curva de intersección es\( (x^2+z^2−1)^3−x^2z^3=0.\)

    60) [T] El toro anular simétrico alrededor del\(z\) eje -es un tipo especial de superficie en topología y su ecuación viene dada por\( (x^2+y^2+z^2+R^2−r^2)^2=4R^2(x^2+y^2)\), donde\( R>r>0\). Los números\( R\) y\( r\) se denominan son los radios mayor y menor, respectivamente, de la superficie. En la siguiente figura se muestra un toro anular para el cual\( R=2\) y\( r=1\).

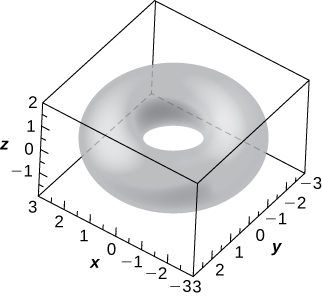
    a. Escriba la ecuación del toro anular con\( R=2\) y\( r=1\), y use un CAS o CalcPlot3D para graficar la superficie. Compara la gráfica con la figura dada.

    b. Determinar la ecuación y esbozar la traza del toro anular de a. en el\(xy\) plano.

    c. Dar dos ejemplos de objetos con formas de toro anular.

    This page titled 12.6E: Ejercicios para la Sección 12.6 is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Edwin “Jed” Herman & Gilbert Strang (OpenStax) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.