13.2: Cálculo de Funciones Vectoriales

Objetivos de aprendizaje

• Escribir una expresión para la derivada de una función con valor vectorial.
• Encuentra el vector tangente en un punto para un vector de posición dado.
• Encuentre el vector tangente unitario en un punto para un vector de posición dado y explique su significado.
• Calcular la integral definida de una función valorada por vector.

Para estudiar el cálculo de las funciones vectoriales, seguimos un camino similar al que tomamos en el estudio de funciones de valor real. Primero, definimos la derivada, luego examinamos las aplicaciones de la derivada, luego pasamos a definir integrales. Sin embargo, encontraremos algunas nuevas ideas interesantes en el camino como resultado de la naturaleza vectorial de estas funciones y las propiedades de las curvas espaciales.

Derivadas de funciones con valores vectoriales

Ahora que hemos visto qué es una función de valor vectorial y cómo tomar su límite, el siguiente paso es aprender a diferenciar una función valorada por vector. La definición de la derivada de una función de valor vectorial es casi idéntica a la definición de una función de valor real de una variable. Sin embargo, debido a que el rango de una función de valor vectorial consiste en vectores, lo mismo es cierto para el rango de la derivada de una función valorada por vector.

Definición: Derivada de funciones con valores vectoriales

La derivada de una función con valor vectorial\(\vecs{r}(t)\) es

\[\vecs{r}′(t) = \lim \limits_{\Delta t \to 0} \dfrac{\vecs{r}(t+\Delta t)−\vecs{r}(t)}{ \Delta t} \label{eq1} \]

siempre que exista el límite. Si\(\vecs{r}'(t)\) existe, entonces\(\vecs{r}(t)\) es diferenciable en\(t\). Si\(\vecs{r}′(t)\) existe para todos\(t\) en un intervalo abierto\((a,b)\) entonces\(\vecs{r}(t)\) es diferenciable sobre el intervalo\((a,b)\). Para que la función sea diferenciable en el intervalo cerrado\([a,b]\), también deben existir los dos límites siguientes:

\[\vecs{r}′(a) = \lim \limits_{\Delta t \to 0^+} \dfrac{\vecs{r}(a+\Delta t)−\vecs{r}(a)}{ \Delta t} \nonumber \]

y

\[\vecs{r}′(b) = \lim \limits_{\Delta t \to 0^-} \dfrac{\vecs{r}(b+\Delta t)−\vecs{r}(b)}{ \Delta t} \nonumber \]

Muchas de las reglas para calcular derivadas de funciones de valor real también se pueden aplicar al cálculo de las derivadas de funciones con valores vectoriales. Recordemos que la derivada de una función de valor real puede interpretarse como la pendiente de una línea tangente o la tasa instantánea de cambio de la función. La derivada de una función de valor vectorial también puede entenderse como una tasa de cambio instantánea; por ejemplo, cuando la función representa la posición de un objeto en un punto dado en el tiempo, la derivada representa su velocidad en ese mismo punto en el tiempo.

Ahora demostramos tomar la derivada de una función valorada por vector.

Ejemplo\(\PageIndex{1}\): Finding the Derivative of a Vector-Valued Function

Usa la definición para calcular la derivada de la función

\[\vecs{r}(t)=(3t+4) \,\mathbf{\hat{i}}+(t^2−4t+3) \,\mathbf{\hat{j}} .\nonumber \]

Solución

Usemos la ecuación\ ref {eq1}:

\ [\ begin {align*}\ vecs {r} ′ (t) &=\ lim\ limits_ {\ Delta t\ a 0}\ dfrac {\ vecs {r} (t+δt) −\ vecs {r} (t)} {Δt}\\ [4pt]
&=\ lim\ límits_ {\ Delta t\ a 0}\ dfrac {(3 (t+δt) +4)\,\ hat {\ mathbf {i}} + ((T+δT) ^2−4 (t+δT) +3)\,\ hat {\ mathbf {j}}] − [(3t+4)\,\ hat {\ mathbf {i}} + (t^2−4t+3)\,\ hat {\ mathbf j {}}]} {Δt}\\ [4 pt]
&=\ lim\ limits_ {\ Delta t\ a 0}\ dfrac {(3t+3δt+4)\,\ hat {\ mathbf {i}} − (3t+4)\,\ hat {\ mathbf {i}} + (t^2+2Tδt+ (Δt) ^2−4T−4δt+3)\,\ hat {\ mathmathbf {j}} − (t^2−4t+3)\,\ hat {\ mathbf {j}}} {Δt}\\ [4pt]
&=\ lim\ limits_ {\ Delta t\ a 0}\ dfrac {(3Δt)\,\ hat {\ mathbf {i}} + (2Tδt+ (Δt) ^2−4Δt)\,\ sombrero {\ mathbf {j}}} {Δt}\\ [4pt]
&=\ lim\ limits_ {\ Delta t\ a 0} (3\,\ hat {\ mathbf {i}} + (2t+δt−4)\,\ hat {\ mathbf {j}})\\ [4pt]
&=3\,\ hat {\ mathbf {i}} + (2t−4)\,\ hat {\ mathbf {j}}\ end {align*}\ nonumber\]

Ejercicio\(\PageIndex{1}\)

Usa la definición para calcular la derivada de la función\(\vecs{r}(t)=(2t^2+3) \,\mathbf{\hat{i}}+(5t−6) \,\mathbf{\hat{j}}\).

Insinuación

Utilice la ecuación\ ref {eq1}.

Contestar

\[\vecs{r}′(t)=4t \,\mathbf{\hat{i}}+5 \,\mathbf{\hat{j}} \nonumber \]

Observe que en los cálculos de Ejemplo\(\PageIndex{1}\), también podríamos obtener la respuesta calculando primero la derivada de cada función componente, luego volviendo a poner estas derivadas en la función valorada por vector. Esto siempre es cierto para calcular la derivada de una función valorada por vector, ya sea en dos o tres dimensiones. Esto lo exponemos en el siguiente teorema. La prueba de este teorema se desprende directamente de las definiciones del límite de una función valorada por vector y la derivada de una función valorada por vector.

Teorema\(\PageIndex{1}\): Differentiation of Vector-Valued Functions

Dejar\(f\),\(g\), y\(h\) ser funciones diferenciables de\(t\).

1. Si\(\vecs{r}(t)=f(t) \,\mathbf{\hat{i}}+g(t) \,\mathbf{\hat{j}}\) entonces\[\vecs{r}′(t)=f′(t) \,\mathbf{\hat{i}}+g′(t) \,\mathbf{\hat{j}}. \nonumber \]
2. Si\(\vecs{r}(t)=f(t) \,\mathbf{\hat{i}}+g(t) \,\mathbf{\hat{j}} + h(t) \,\mathbf{\hat{k}}\) entonces\[\vecs{r}′(t)=f′(t) \,\mathbf{\hat{i}}+g′(t) \,\mathbf{\hat{j}} + h′(t) \,\mathbf{\hat{k}}. \nonumber \]

Ejemplo\(\PageIndex{2}\): Calculating the Derivative of Vector-Valued Functions

Utilice el Teorema\(\PageIndex{1}\) para calcular la derivada de cada una de las siguientes funciones.

1. \(\vecs{r}(t)=(6t+8) \,\mathbf{\hat{i}}+(4t^2+2t−3) \,\mathbf{\hat{j}}\)
2. \(\vecs{r}(t)=3 \cos t \,\mathbf{\hat{i}}+4 \sin t \,\mathbf{\hat{j}}\)
3. \(\vecs{r}(t)=e^t \sin t \,\mathbf{\hat{i}}+e^t \cos t \,\mathbf{\hat{j}}−e^{2t} \,\mathbf{\hat{k}}\)

Solución

Utilizamos Teorema\(\PageIndex{1}\) y lo que sabemos sobre la diferenciación de funciones de una variable.

1. El primer componente de\[\vecs r(t)=(6t+8) \,\mathbf{\hat{i}}+(4t^2+2t−3) \,\mathbf{\hat{j}} \nonumber \] es\(f(t)=6t+8\). El segundo componente es\(g(t)=4t^2+2t−3\). Tenemos\(f′(t)=6\) y\(g′(t)=8t+2\), así\(\PageIndex{1}\) da el Teorema\(\vecs r′(t)=6 \,\mathbf{\hat{i}}+(8t+2)\,\mathbf{\hat{j}}\).
2. El primer componente es\(f(t)=3 \cos t\) y el segundo componente es\(g(t)=4 \sin t\). Tenemos\(f′(t)=−3 \sin t\) y\(g′(t)=4 \cos t\), así obtenemos\(\vecs r′(t)=−3 \sin t \,\mathbf{\hat{i}}+4 \cos t \,\mathbf{\hat{j}}\).
3. El primer componente de\(\vecs r(t)=e^t \sin t \,\mathbf{\hat{i}}+e^t \cos t \,\mathbf{\hat{j}}−e^{2t} \,\mathbf{\hat{k}}\) es\(f(t)=e^t \sin t\), el segundo componente es\(g(t)=e^t \cos t\), y el tercer componente es\(h(t)=−e^{2t}\). Tenemos\(f′(t)=e^t(\sin t+\cos t)\),\(g′(t)=e^t (\cos t−\sin t)\), y\(h′(t)=−2e^{2t}\), así el teorema da\(\vecs r′(t)=e^t(\sin t+\cos t)\,\mathbf{\hat{i}}+e^t(\cos t−\sin t)\,\mathbf{\hat{j}}−2e^{2t} \,\mathbf{\hat{k}}\).

Ejercicio\(\PageIndex{2}\)

Calcular la derivada de la función

\[\vecs{r}(t)=(t \ln t)\,\mathbf{\hat{i}}+(5e^t) \,\mathbf{\hat{j}}+(\cos t−\sin t) \,\mathbf{\hat{k}}. \nonumber \]

Insinuación

Identificar las funciones componentes y utilizar Teorema\(\PageIndex{1}\).

Contestar

\[\vecs{r}′(t)=(1+ \ln t) \,\mathbf{\hat{i}}+5e^t \,\mathbf{\hat{j}}−(\sin t+\cos t)\,\mathbf{\hat{k}} \nonumber \]

Podemos extender a las funciones vectoriales las propiedades de la derivada que presentamos anteriormente. En particular, la regla múltiple constante, las reglas de suma y diferencia, la regla de producto y la regla de cadena se extienden a funciones de valor vectorial. Sin embargo, en el caso de la regla del producto, en realidad hay tres extensiones:

1. para una función de valor real multiplicada por una función de valor vectorial,
2. para el producto punto de dos funciones con valor vectorial, y
3. para el producto cruzado de dos funciones vectoriales.

Teorema: Propiedades de la Derivada de Funciones Vectoriales

Dejar\(\vecs{r}\) y\(\vecs{u}\) ser funciones vectoriales diferenciables de\(t\), dejar\(f\) ser una función diferenciable de valor real de\(t\), y dejar\(c\) ser un escalar.

\[\begin{array}{lrcll} \mathrm{i.} & \dfrac{d}{\,dt}[c\vecs r(t)] & = & c\vecs r′(t) & \text{Scalar multiple} \nonumber\\ \mathrm{ii.} & \dfrac{d}{\,dt}[\vecs r(t)±\vecs u(t)] & = & \vecs r′(t)±\vecs u′(t) & \text{Sum and difference} \nonumber\\ \mathrm{iii.} & \dfrac{d}{\,dt}[f(t)\vecs u(t)] & = & f′(t)\vecs u(t)+f(t)\vecs u′(t) & \text{Scalar product} \nonumber\\ \mathrm{iv.} & \dfrac{d}{\,dt}[\vecs r(t)⋅\vecs u(t)] & = & \vecs r′(t)⋅\vecs u(t)+\vecs r(t)⋅\vecs u′(t) & \text{Dot product} \nonumber\\ \mathrm{v.} & \dfrac{d}{\,dt}[\vecs r(t)×\vecs u(t)] & = & \vecs r′(t)×\vecs u(t)+\vecs r(t)×\vecs u′(t) & \text{Cross product} \nonumber\\ \mathrm{vi.} & \dfrac{d}{\,dt}[\vecs r(f(t))] & = & \vecs r′(f(t))⋅f′(t) & \text{Chain rule} \nonumber\\ \mathrm{vii.} & \text{If} \; \vecs r(t)·\vecs r(t) & = & c, \text{then} \; \vecs r(t)⋅\vecs r′(t) \; =0 \; . & \mathrm{} \nonumber \end{array} \nonumber \]

Prueba

Las pruebas de las dos primeras propiedades se derivan directamente de la definición de la derivada de una función valorada por vector. La tercera propiedad se puede derivar de las dos primeras propiedades, junto con la regla del producto. Vamos\(\vecs u(t)=g(t)\,\mathbf{\hat{i}}+h(t)\,\mathbf{\hat{j}}\). Entonces

\ [\ begin {alinear*}\ dfrac {d} {\, dt} [f (t)\ vecs u (t)] &=\ dfrac {d} {\, dt} [f (t) (g (t)\,\ mathbf {\ hat {i}} +h (t)\,\ mathbf {\ hat {j}})]\ [4pt]
&=\ dfrac {d} {\, dt} [f (t) g (t)\,\ mathbf {\ hat {i}} +f (t) h (t)\,\ mathbf {\ hat {j}}]\\ [4pt]
&=\ dfrac {d} {\, dt} [f (t) g (t)]\,\ mathbf {\ sombrero {i}} +\ dfrac {d} {\, dt} [f (t) h (t)]\,\ mathbf {\ hat {j}}\\ [4pt]
&= (f′ (t) g (t) +f (t) g′ (t))\,\ mathbf {\ hat {i}} + (f′ (t) h (t) +f (t) h′ (t))\,\ mathbf {\ hat {j}}\\ [4pt]
&=f′ (t)\ vecs u (t) +f (t)\ vecs u′ (t). \ end {align*}\ nonumber\]

Para acreditar propiedad iv. dejar\(\vecs r(t)=f_1(t) \,\mathbf{\hat{i}}+g_1(t) \,\mathbf{\hat{j}}\) y\(\vecs u(t)=f_2(t) \,\mathbf{\hat{i}}+g_2(t) \,\mathbf{\hat{j}}\). Entonces

\ [\ begin {align*}\ dfrac {d} {\, dt} [\ vecs r (t) ⋅\ vecs u (t)] &=\ dfrac {d} {\, dt} [f_1 (t) f_2 (t) +g_1 (t) g_2 (t)]\\ [4pt]
&=f_1′ (t) f_2 (t) +f_1 (t) f_2′ (t) +g_1′ (t) g_2 (t) +g_1 (t) g_2′ (t) =f_1′ (t) f_2 (t) +g_1′ (t) g_2 (t) +f_1 (t) f_2′ (t) +g_1 (t) g_2′ (t)\\ [4pt]
& =( f_1′\,\ mathbf {\ hat {i}} +g_1′\,\ mathbf {\ hat {j}}) ⋅ (f_2\,\ mathbf {\ hat {i}} +g_2\,\ mathbf {\ hat {j}}) + (f_1\,\ mathbf {\ hat {i}} +g_1\,\ mathbf {\ hat {j}}) ⋅ (f_2′\,\ mathbf {\ hat {i}} +ggbf _2′\,\ mathbf {\ hat {j}})\\ [4pt]
&=\ vecs r′ (t) ⋅\ vecs u (t) +\ vecs r (t) ⋅\ vecs u′ (t). \ end {align*}\ nonumber\]

El comprobante de propiedad v. es similar a la de propiedad iv. La propiedad vi. se puede probar usando la regla de la cadena. Por último, el inmueble vii. se desprende del inmueble iv:

\ [\ begin {align*}\ dfrac {d} {\, dt} [\ vecs r (t) ·\ vecs r (t)] &=\ dfrac {d} {\, dt} [c]\\ [4pt]
\ vecs r′ (t) ·\ vecs r (t) +\ vecs r (t) ·\ vecs r′ (t) = 0\\ [4pt]
2\ vecs r (t) ·\ vecs r′ (t) &= 0\\ [4pt]
\ vecs r (t) ·\ vecs r′ (t) &= 0\ end {align*}\ nonumber\]

Ahora para algunos ejemplos usando estas propiedades.

Ejemplo\(\PageIndex{3}\): Using the Properties of Derivatives of Vector-Valued Functions

Dadas las funciones vectoriales

\[\vecs{r}(t)=(6t+8)\,\mathbf{\hat{i}}+(4t^2+2t−3)\,\mathbf{\hat{j}}+5t \,\mathbf{\hat{k}} \nonumber \]

y

\[\vecs{u}(t)=(t^2−3)\,\mathbf{\hat{i}}+(2t+4)\,\mathbf{\hat{j}}+(t^3−3t)\,\mathbf{\hat{k}}, \nonumber \]

calcular cada una de las siguientes derivadas utilizando las propiedades de la derivada de funciones con valor vectorial.

1. \(\dfrac{d}{\,dt}[\vecs{r}(t)⋅ \vecs{u}(t)]\)
2. \(\dfrac{d}{\,dt}[ \vecs{u} (t) \times \vecs{u}′(t)]\)

Solución

Tenemos\(\vecs{r}′(t)=6 \,\mathbf{\hat{i}}+(8t+2) \,\mathbf{\hat{j}}+5 \,\mathbf{\hat{k}}\) y\(\vecs{u}′(t)=2t \,\mathbf{\hat{i}}+2 \,\mathbf{\hat{j}}+(3t^2−3) \,\mathbf{\hat{k}}\). Por lo tanto, de acuerdo con la propiedad iv:

1. \ [\ begin {align*}\ dfrac {d} {\, dt} [\ vecs r (t) ⋅\ vecs u (t)] &=\ vecs r′ (t) ⋅\ vecs u (t) +\ vecs r (t) ⋅\ vecs u′ (t)\\ [4pt]
   &= (6\,\ mathbf {\ hat {i} + (8t+2)\,\ mathbf {\ hat {j}} +5\,\ mathbf {\ hat {k}}) ⋅ ((t^2−3)\,\ mathbf {\ hat {i}} + (2t+4)\,\ mathbf {\ hat {j}} + (t^3−3t)\,\ mathbf {\ hat {k}})\\ [4pt]
   &\; + ((6t+8)\,\ mathbf {\ hat {i}} + (4t^2+2t−3)\,\ mathbf {\ hat {j}} +5t\,\ mathbf {\ hat {k}}) ⋅ (2t\,\ mathbf {\ hat {i}} +2\,\ mathbf {\ hat {j}} + (3t t^2−3)\,\ mathbf {\ hat {k}})\\ [4pt]
   &= 6 (t^2−3) + (8t+2) (2t+4) +5 (t^3−3t)\\ [4pt]
   &\; +2t (6t+8) +2 (4t^2+2t−3) +5t (3t^2−3)\\ [4pt ]
   &= 20t^3+42t^2+26t−16. \ end {alinear*}\]
2. Primero, necesitamos adaptar la propiedad v para este problema:

   \[\dfrac{d}{\,dt}[ \vecs{u}(t) \times \vecs{u}′(t)]=\vecs{u}′(t)\times \vecs{u}′(t)+ \vecs{u}(t) \times \vecs{u}′′(t). \nonumber \]

   Recordemos que el producto cruzado de cualquier vector consigo mismo es cero. Además,\(\vecs u′′(t)\) representa la segunda derivada de\(\vecs u(t):\)

   \[\vecs u′′(t)=\dfrac{d}{\,dt}[\vecs u′(t)]=\dfrac{d}{\,dt}[2t \,\mathbf{\hat{i}}+2 \,\mathbf{\hat{j}}+(3t^2−3) \,\mathbf{\hat{k}}]=2 \,\mathbf{\hat{i}}+6t \,\mathbf{\hat{k}}. \nonumber \]

   Por lo tanto,

   \ [\ begin {align*}\ dfrac {d} {\, dt} [\ vecs u (t)\ times\ vecs u′ (t)] &=0+ ((t^2−3)\,\ hat {\ mathbf {i}} + (2t+4)\,\ hat {\ mathbf {j}} + (t^3−3t)\,\ hat {\ mathbf {k}})\ times (2\,\ hat {\ mathbf {i}} +6t\,\ hat {\ mathbf {k}})\\ [4pt]
   &=\ begin {vmatrix}\,\ hat {\ mathbf {i}} &\,\ hat {\ mathbf {j}} &\,\ hat {\ mathbf {k}}\\ t^2-3 & 2t+4 & t^3 -3t\\ 2 & 0 & 6t\ end {vmatrix}\\ [4pt]
   & =6t (2t+4)\,\ hat {\ mathbf {i}} − (6t (t^2−3) −2 (t^3−3t))\,\ hat {\ mathbf j {}} −2 (2t+4)\,\ hat {\ mathbf {k}}\\ [4pt]
   & =( 12t^2+24t)\,\ hat {\ mathbf {i}} + (12t−4t^3)\,\ hat {\ mathbf {j}} − (4t+8)\, \ hat {\ mathbf {k}}. \ end {alinear*}\]

Ejercicio\(\PageIndex{3}\)

Calcular\(\dfrac{d}{\,dt}[\vecs{r}(t)⋅ \vecs{r}′(t)]\) y\( \dfrac{d}{\,dt}[\vecs{u}(t) \times \vecs{r}(t)]\) para las funciones vectorizadas:

• \(\vecs{r}(t)=\cos t \,\mathbf{\hat{i}}+ \sin t \,\mathbf{\hat{j}}−e^{2t} \,\mathbf{\hat{k}}\)
• \(\vecs{u}(t)=t \,\mathbf{\hat{i}}+ \sin t \,\mathbf{\hat{j}}+ \cos t \,\mathbf{\hat{k}}\),

Insinuación

Siga los mismos pasos que en Ejemplo\(\PageIndex{3}\).

Contestar

\(\dfrac{d}{\,dt}[\vecs{r}(t)⋅ \vecs{r}′(t)]=8e^{4t}\)

\( \dfrac{d}{\,dt}[ \vecs{u}(t) \times \vecs{r}(t)] =−(e^{2t}(\cos t+2 \sin t)+ \cos 2t) \,\mathbf{\hat{i}}+(e^{2t}(2t+1)− \sin 2t) \,\mathbf{\hat{j}}+(t \cos t+ \sin t− \cos 2t) \,\mathbf{\hat{k}}\)

Vectores tangentes y vectores tangentes unitarios

Recordemos que la derivada en un punto puede interpretarse como la pendiente de la línea tangente a la gráfica en ese punto. En el caso de una función con valor vectorial, la derivada proporciona un vector tangente a la curva representada por la función. Considere la función de valor vectorial

\[\vecs{r}(t)=\cos t \,\mathbf{\hat{i}} + \sin t \,\mathbf{\hat{j}} \label{eq10} \]

La derivada de esta función es

\[\vecs{r}′(t)=−\sin t \,\mathbf{\hat{i}} + \cos t \,\mathbf{\hat{j}} \nonumber \]

Si sustituimos el valor\(t=π/6\) en ambas funciones obtenemos

\[\vecs{r} \left(\dfrac{π}{6}\right)=\dfrac{\sqrt{3}}{2} \,\mathbf{\hat{i}}+\dfrac{1}{2}\,\mathbf{\hat{j}} \nonumber \]

y

\[ \vecs{r}′ \left(\dfrac{π}{6} \right)=−\dfrac{1}{2}\,\mathbf{\hat{i}}+\dfrac{\sqrt{3}}{2}\,\mathbf{\hat{j}}. \nonumber \]

La gráfica de esta función aparece en la Figura\(\PageIndex{1}\), junto con los vectores\(\vecs{r}\left(\dfrac{π}{6}\right)\) y\(\vecs{r}' \left(\dfrac{π}{6}\right)\).

Figura\(\PageIndex{1}\): La línea tangente en un punto se calcula a partir de la derivada de la función valorada por vector\(\vecs{r}(t)\).

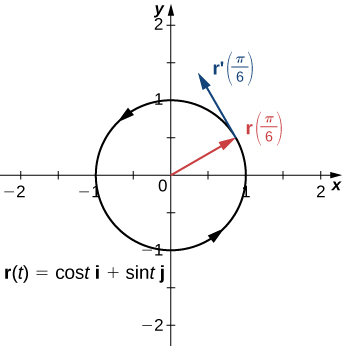
Observe que el vector\(\vecs{r}′\left(\dfrac{π}{6}\right)\) es tangente al círculo en el punto correspondiente a\(t=\dfrac{π}{6}\). Este es un ejemplo de un vector tangente a la curva plana definida por la Ecuación\ ref {eq10}.

Definición: vector tangente de unidad principal

Dejar\(C\) ser una curva definida por una función de valor vectorial\(\vecs{r}\), y asumir que\(\vecs{r}′(t)\) existe cuando\(\mathrm{t=t_0}\) Un vector tangente\(\vecs{r}\) at\(t=t_0\) es cualquier vector tal que, cuando la cola del vector se coloca en el punto\(\vecs r(t_0)\) de la gráfica, el vector\(\vecs{r}\) es tangente a la curva \(C\). Vector\(\vecs{r}′(t_0)\) es un ejemplo de un vector tangente en el punto\(t=t_0\). Además, supongamos que\(\vecs{r}′(t)≠0\). El vector tangente de unidad principal en\(t\) se define como

\[\vecs{T}(t)=\dfrac{ \vecs{r}′(t)}{‖\vecs{r}′(t)‖}, \nonumber \]

siempre\(‖\vecs{r}′(t)‖≠0\).

El vector tangente unitario es exactamente lo que parece: un vector unitario que es tangente a la curva. Para calcular un vector tangente unitario, primero encuentra la derivada\(\vecs{r}′(t)\). Segundo, calcular la magnitud de la derivada. El tercer paso es dividir la derivada por su magnitud.

Ejemplo\(\PageIndex{4}\): Finding a Unit Tangent Vector

Encuentre el vector tangente unitario para cada una de las siguientes funciones con valores vectoriales:

1. \(\vecs{r}(t)=\cos t \,\mathbf{\hat{i}}+\sin t \,\mathbf{\hat{j}}\)
2. \(\vecs{u}(t)=(3t^2+2t) \,\mathbf{\hat{i}}+(2−4t^3)\,\mathbf{\hat{j}}+(6t+5)\,\mathbf{\hat{k}}\)

Solución

1. \(\begin{array}{lrcl} \text{First step:} & \vecs r′(t) & = & − \sin t \,\hat{\mathbf{i}}+ \cos t \,\hat{\mathbf{j}} \\ \text{Second step:} & ‖\vecs r′(t)‖ & = & \sqrt{(− \sin t)^2+( \cos t)^2} = 1 \\ \text{Third step:} & \vecs T(t) & = & \dfrac{\vecs r′(t)}{‖\vecs r′(t)‖}=\dfrac{− \sin t \,\hat{\mathbf{i}}+ \cos t \,\hat{\mathbf{j}}}{1}=− \sin t \,\hat{\mathbf{i}}+ \cos t \,\hat{\mathbf{j}} \end{array}\)
2. \(\begin{array}{lrcl} \text{First step:} & \vecs r′(t) & = & (6t+2) \,\hat{\mathbf{i}}−12t^2 \,\hat{\mathbf{j}}+6 \,\hat{\mathbf{k}} \\ \text{Second step:} & ‖\vecs r′(t)‖ & = & \sqrt{(6t+2)^2+(−12t^2)^2+6^2} \\ \text{} & \text{} & = & \sqrt{144t^4+36t^2+24t+40} \\ \text{} & \text{} & = & 2 \sqrt{36t^4+9t^2+6t+10} \\ \text{Third step:} & \vecs T(t) & = & \dfrac{\vecs r′(t)}{‖\vecs r′(t)‖}=\dfrac{(6t+2) \,\hat{\mathbf{i}}−12t^2 \,\hat{\mathbf{j}}+6 \,\hat{\mathbf{k}}}{2 \sqrt{36t^4+9t^2+6t+10}} \\ \text{} & \text{} & = & \dfrac{3t+1}{\sqrt{36t^4+9t^2+6t+10}} \,\hat{\mathbf{i}} - \dfrac{6t^2}{\sqrt{36t^4+9t^2+6t+10}} \,\hat{\mathbf{j}} + \dfrac{3}{\sqrt{36t^4+9t^2+6t+10}} \,\hat{\mathbf{k}} \end{array}\)

Ejercicio\(\PageIndex{4}\)

Encuentra el vector de tangente unitaria para la función de valor vectorial

\[\vecs r(t)=(t^2−3)\,\mathbf{\hat{i}}+(2t+1) \,\mathbf{\hat{j}}+(t−2) \,\mathbf{\hat{k}}. \nonumber \]

Insinuación

Siga los mismos pasos que en Ejemplo\(\PageIndex{4}\).

Contestar

\[\vecs T(t)=\dfrac{2t}{\sqrt{4t^2+5}}\,\mathbf{\hat{i}}+\dfrac{2}{\sqrt{4t^2+5}}\,\mathbf{\hat{j}}+\dfrac{1}{\sqrt{4t^2+5}}\,\mathbf{\hat{k}} \nonumber \]

Integrales de funciones con valores vectoriales

Introdujimos antiderivados de funciones de valor real en Antiderivados e integrales definidas de funciones de valor real en La Integral Definida. Cada uno de estos conceptos se puede extender a funciones con valores vectoriales. Además, así como podemos calcular la derivada de una función valorada por vector diferenciando las funciones componentes por separado, podemos calcular la antiderivada de la misma manera. Además, el Teorema Fundamental del Cálculo se aplica también a las funciones vectoriales.

La antiderivada de una función vectorizada aparece en las aplicaciones. Por ejemplo, si una función con valor vectorial representa la velocidad de un objeto en el tiempo t, entonces su antiderivada representa la posición. O bien, si la función representa la aceleración del objeto en un momento dado, entonces la antiderivada representa su velocidad.

Definición: Integrales definidas e indefinidas de funciones vectoriales

Dejar\(f\)\(g\), y\(h\) ser integrables funciones de valor real en el intervalo cerrado\([a,b].\)

1. La integral indefinida de una función con valor vectorial\(\vecs{r}(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}\) es

   \[\int [f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}]\,dt= \left[ \int f(t)\,dt \right] \,\hat{\mathbf{i}}+ \left[ \int g(t)\,dt \right] \,\hat{\mathbf{j}}. \nonumber \]

   La integral definida de una función de valor vectorial es

   \[\int_a^b [f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}]\,dt = \left[ \int_a^b f(t)\,dt \right] \,\hat{\mathbf{i}}+ \left[ \int_a^b g(t)\,dt \right] \,\hat{\mathbf{j}}. \nonumber \]

2. La integral indefinida de una función con valor vectorial\(\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}+h(t) \,\hat{\mathbf{k}}\) es

   \[\int [f(t) \,\hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}} + h(t) \,\hat{\mathbf{k}}]\,dt= \left[ \int f(t)\,dt \right] \,\hat{\mathbf{i}}+ \left[ \int g(t)\,dt \right] \,\hat{\mathbf{j}} + \left[ \int h(t)\,dt \right] \,\hat{\mathbf{k}}. \nonumber \]

   La integral definida de la función vectorizada es

   \[\int_a^b [f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}} + h(t) \,\hat{\mathbf{k}}]\,dt= \left[ \int_a^b f(t)\,dt \right] \,\hat{\mathbf{i}}+ \left[ \int_a^b g(t)\,dt \right] \,\hat{\mathbf{j}} + \left[ \int_a^b h(t)\,dt \right] \,\hat{\mathbf{k}}. \nonumber \]

Dado que la integral indefinida de una función de valor vectorial implica integrales indefinidas de las funciones componentes, cada una de estas integrales componentes contiene una constante de integración. Todos pueden ser diferentes. Por ejemplo, en el caso bidimensional, podemos tener

\[\int f(t)\,dt=F(t)+C_1 \; and \; \int g(t)\,dt=G(t)+C_2, \nonumber \]

donde\(F\) y\(G\) son antiderivados de\(f\) y\(g\), respectivamente. Entonces

\ [\ begin {align*}\ int [f (t)\,\ hat {\ mathbf {i}} +g (t)\,\ hat {\ mathbf {j}}]\, dt &=\ izquierda [\ int f (t)\, dt\ derecha]\,\ hat {\ mathbf {i}} +\ izquierda [\ int g (t)\, dt\ derecha]\,\ hat {\ mathbf {j}}\\ [4pt]
&= (F (t) +C_1)\,\ hat {\ mathbf {i}} + (G (t) +C_2)\,\ hat {\ mathbf {j}}\\ [4pt]
&=F (t)\,\ hat {\ mathbf {i}} +G (t)\,\ hat {\ mathbf {j}} +C_1\,\ hat {\ mathbf {i}} +C_2\,\ hat {\ mathbf {j}}\\ [4pt]
&= F (t)\,\ hat {\ mathbf {i}} +G (t)\,\ hat {\ mathbf {j}} +\ vecs {C}\ final {alinear*}\]

donde\(\vecs{C}=C_1 \,\hat{\mathbf{i}}+C_2 \,\hat{\mathbf{j}}\). Por lo tanto, las constantes de integración se convierten en un vector constante.

Ejemplo\(\PageIndex{5}\): Integrating Vector-Valued Functions

Calcula cada una de las siguientes integrales:

1. \( \displaystyle \int [(3t^2+2t) \,\hat{\mathbf{i}}+(3t−6) \,\hat{\mathbf{j}}+(6t^3+5t^2−4) \,\hat{\mathbf{k}}]\,dt\)
2. \( \displaystyle \int [⟨t,t^2,t^3⟩ \times ⟨t^3,t^2,t⟩] \,dt\)
3. \( \displaystyle \int_{0}^{\frac{\pi}{3}} [\sin 2t \,\hat{\mathbf{i}}+ \tan t \,\hat{\mathbf{j}}+e^{−2t} \,\hat{\mathbf{k}}]\,dt\)

Solución

1. Utilizamos la primera parte de la definición de la integral de una curva espacial:
2. \ [\ begin {align*}\ int [(3t^2+2t)\,\ hat {\ mathbf {i}} + (3t−6)\,\ hat {\ mathbf {j}} + (6t^3+5t^2−4)\,\ hat {\ mathbf {k}}]\, dt &=\ left [\ int 3t^2+2t\, dt\ derecha]\,\ hat {\ mathbf {i}} +\ izquierda [\ int 3t−6\, dt\ derecha]\,\ hat {\ mathbf {j}} +\ izquierda [\ int 6t^3+5t^2−4\, dt\ derecha]\,\ hat {\ mathbf {k}}\\ [4pt]
   & =( t^3+t^2) \,\ hat {\ mathbf {i}} +\ izquierda (\ frac {3} {2} t^2−6t\ derecha)\,\ hat {\ mathbf {j}} +\ izquierda (\ frac {3} {2} t^4+\ frac {5} {3} t^3−4t\ derecha)\,\ sombrero {\ mathbf {k}} +\ vecs C.\ final {alinear*}\]
3. Primero calcule\(⟨t,t^2,t^3⟩ \times ⟨t^3,t^2,t⟩:\)

   \ [\ begin {align*} ⟩ t, t^2, t^3⟩\ veces +52 t^3, t^2, t⟩ &=\ begin {vmatrix}\ hat {\ mathbf {i}} &\,\ hat {\ mathbf {j}} &\,\ hat {\ mathbf {k}}\ t & t^2 & t^3\ t^3 & t^3 & t^3 & t^3 & t^3 & t^3 & t^3 & t^3 & t^3 & t^^2 & t\ end {vmatrix}\\ [4pt]
   &= (t^2 (t) −t^3 (t^2))\,\ hat {\ mathbf {i}} − (t^2−t^3 (t^3))\,\ hat {\ mathbf {j}} + (t (t^2) −t ^2 (t^3))\,\ hat {\ mathbf {k}}\\ [4pt]
   & =( t^3−t^5)\,\ hat {\ mathbf {i}} + (t^6−t^2)\,\ hat {\ mathbf {j}} + (t^3−t^5)\,\ hat {\ mathbf {k}}. \ end {align*}\ nonumber\]

   A continuación, sustituya esto de nuevo en lo integral e integre:

   \ [\ begin {alinear*}\ int [ƒt, t^2, t^3⟩\ veces +52 t^3, t^2, t⟩]\, dt &=\ int (t^3−t^5)\,\ hat {\ mathbf {i}} + (t^6−t^2)\,\ hat {\ mathbf {j}} + (t^3−t^2)\,\ hat {\ mathbf {j} + (t^3−t^2)\,\ hat {j} 5)\,\ hat {\ mathbf {k}}\, dt\\ [4pt]
   &=\ left (\ frac {t^4} {4} −\ frac {t^6} {6}\ derecha)\,\ hat {\ mathbf {i}} +\ left (\ frac {t^7} {7} −\ frac {t^3}\ derecha)\,\ hat {\ mathbf {j}} +\ izquierda (\ frac {t^4} {4} −\ frac {t^6} {6}\ derecha)\,\ hat {\ mathbf {k}} +\ vecs C.\ end {align*}\]

4. Utilice la segunda parte de la definición de la integral de una curva espacial:

   \ [\ begin {align*}\ int_0^ {\ frac {\ pi} {3}} [\ sin 2t\,\ hat {\ mathbf {i}} +\ tan t\,\ hat {\ mathbf {j}} +e^ {−2t}\,\ hat {\ mathbf {k}}]\, dt &=\ left [\ int_0^ {frac {π} {3}}\ sin 2t\, dt\ derecha]\,\ sombrero {\ mathbf {i}} +\ izquierda [\ int_0^ {\ frac {π} {3}}\ tan t\, dt\ derecha]\,\ sombrero {\ mathbf {j}} +\ izquierda [\ int_0^ {\ frac {π} {3}} e^ {−2t}\, dt\ derecha] \,\ hat {\ mathbf {k}}\\ [4pt]
   &= (-\ tfrac {1} {2}\ cos 2t)\ Grande\ vert_ {0} ^ {π/3}\,\ hat {\ mathbf {i}} − (\ ln |\ cos t|)\ Grande\ vert_ {0} ^ {π/3}\,\ sombrero {\ mathbf {j}} −\ izquierda (\ tfrac {1} {2} e^ {−2t}\ derecha)\ Grande\ vert_ {0} ^ {π/3}\,\ hat {\ mathbf {k}}\\ [4pt]
   &=\ left (−\ tfrac {1} {2}\ cos\ tfrac {2π} {3} +\ tfrac {1} {2}\ cos 0\ derecha)\,\ hat {\ mathbf {i}} −\ izquierda (\ ln\ izquierda (\ cos\ tfrac {π} {3}\ derecha) −\ ln (\ cos 0)\ derecha)\,\ hat {\ mathbf {j}} −\ izquierda (\ tfrac {1} {2} e^ {−2πp /3} −\ tfrac {1} {2} e^ {−2 (0)}\ derecha)\,\ hat {\ mathbf {k}}\\ [4pt]
   & =\ left (\ tfrac {1} {4} +\ tfrac {1} {2}\ derecha)\,\ hat {\ mathbf {i}} − (−\ ln 2)\,\ sombrero {\ mathbf {j}} −\ izquierda (\ tfrac {1} {2} e^ {−2π/3} −\ tfrac {1} {2}\ derecha)\,\ hat {\ mathbf {k}}\\ [4pt]
   &=\ tfrac {3} {4}\,\ hat {\ mathbf {i}} + (\ ln 2)\,\ hat {\ mathbf {j}} +\ left (\ tfrac {1} {2} −\ tfrac {1} {2} e^ {−2π/3}\ derecha)\,\ hat {\ mathbf {k}}. \ end {alinear*}\]

Ejercicio\(\PageIndex{5}\)

Calcular la siguiente integral:

\[\int_1^3 [(2t+4) \,\mathbf{\hat{i}}+(3t^2−4t) \,\mathbf{\hat{j}}]\,dt \nonumber \]

Pista

Utilice la definición de la integral definida de una curva plana.

Contestar

\[\int_1^3 [(2t+4) \,\mathbf{\hat{i}}+(3t^2−4t) \,\mathbf{\hat{j}}]\,dt = 16 \,\mathbf{\hat{i}}+10 \,\mathbf{\hat{j}} \nonumber \]

Resumen

• Para calcular la derivada de una función con valor vectorial, calcule las derivadas de las funciones componentes, luego vuelva a colocarlas en una nueva función valorada por vector.
• Muchas de las propiedades de diferenciación de funciones escalares también se aplican a las funciones con valores vectoriales.
• La derivada de una función con valor vectorial\(\vecs r(t)\) es también un vector tangente a la curva. El vector tangente unitario\(\vecs T(t)\) se calcula dividiendo la derivada de una función valorada por vector por su magnitud.
• La antiderivada de una función valorada por vector se encuentra encontrando las antiderivadas de las funciones componentes, luego poniéndolas de nuevo juntas en una función valorada por vector.
• La integral definida de una función valorada por vector se encuentra encontrando las integrales definidas de las funciones componentes, luego poniéndolas de nuevo juntas en una función valorada por vector.

Ecuaciones Clave

• Derivada de una función valorada por vector\[\vecs r′(t) = \lim \limits_{\Delta t \to 0} \dfrac{\vecs r(t+\Delta t)−\vecs r(t)}{ \Delta t} \nonumber \]
• Vector tangente de unidad principal\[\vecs T(t)=\frac{\vecs r′(t)}{‖\vecs r′(t)‖} \nonumber \]
• Integral indefinida de una función de valor vectorial\[\int [f(t) \,\mathbf{\hat{i}}+g(t)\,\mathbf{\hat{j}} + h(t) \,\mathbf{\hat{k}}]\,dt= \left[ \int f(t)\,dt \right] \,\mathbf{\hat{i}}+ \left[ \int g(t)\,dt \right] \,\mathbf{\hat{j}} + \left[ \int h(t)\,dt \right] \,\mathbf{\hat{k}}\nonumber \]
• Integral definida de una función valorada por vector\[\int_a^b [f(t) \,\mathbf{\hat{i}}+g(t) \,\mathbf{\hat{j}} + h(t) \,\mathbf{\hat{k}}]\,dt= \left[\int_a^b f(t)\,dt \right] \,\mathbf{\hat{i}}+ \left[ \int _a^b g(t)\,dt \right] \,\mathbf{\hat{j}} + \left[ \int _a^b h(t)\,dt \right] \,\mathbf{\hat{k}}\nonumber \]

Glosario

integral definida de una función valorada por vector

el vector obtenido calculando la integral definida de cada una de las funciones componentes de una función valorada por vector dada, luego usando los resultados como los componentes de la función resultante

derivada de una función valorada por vector

la derivada de una función con valor vectorial\(\vecs{r}(t)\) es\(\vecs{r}′(t) = \lim \limits_{\Delta t \to 0} \frac{\vecs r(t+\Delta t)−\vecs r(t)}{ \Delta t}\), siempre que exista el límite

integral indefinida de una función con valor vectorial

una función de valor vectorial con una derivada que es igual a una función valorada por vector dada

unidad principal, tangente, vector

un vector unitario tangente a una curva C

vector tangente

a\(\vecs{r}(t)\) en\(t=t_0\) cualquier vector\(\vecs v\) tal que, cuando la cola del vector se coloca en el punto\(\vecs r(t_0)\) de la gráfica, el vector\(\vecs{v}\) es tangente a la curva C