13.3E: Ejercicios para la Sección 13.3

Determinación de la longitud del arco

En las preguntas 1 a 5, encuentra la longitud del arco de la curva en el intervalo dado.

1)\(\vecs r(t)=t^2 \,\hat{\mathbf{i}}+(2t^2+1)\,\hat{\mathbf{j}}, \quad 1≤t≤3\)

Responder

\(8\sqrt{5}\)unidades

2)\(\vecs r(t)=t^2 \,\hat{\mathbf{i}}+14t \,\hat{\mathbf{j}},\quad 0≤t≤7\). Esta parte de la gráfica se muestra aquí:

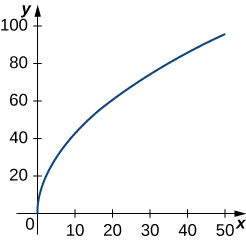
3)\(\vecs r(t)=⟨t^2+1,4t^3+3⟩, \quad −1≤t≤0\)

Responder

\(\frac{1}{54}(37^{3/2}−1)\)unidades

4)\(\vecs r(t)=⟨2 \sin t,5t,2 \cos t⟩,\quad 0≤t≤π\). Esta parte de la gráfica se muestra aquí:

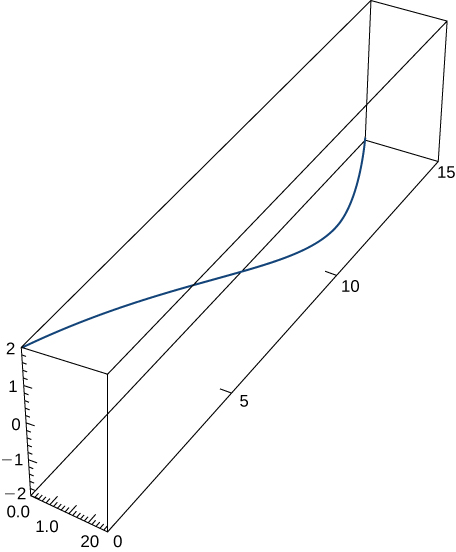
5)\(\vecs r(t)=⟨e^{−t \cos t},e^{−t \sin t}⟩\) en el intervalo\([0,\frac{π}{2}]\). Aquí está la porción de la gráfica en el intervalo indicado:

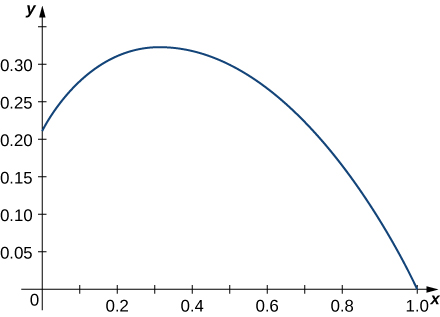
6) Configura una integral para representar la longitud del arco de\(t = 0\) a\(t = 2\) lo largo de la curva trazada por\(\vecs r(t) = \langle t, \, t^4\rangle.\) Luego usa la tecnología para aproximar esta longitud a la milésima de unidad más cercana.

7) Encuentra la longitud de una vuelta de la hélice dada por\(\vecs r(t)= \frac{1}{2} \cos t \,\hat{\mathbf{i}}+\frac{1}{2} \sin t \,\hat{\mathbf{j}}+\frac{\sqrt{3}}{2}\,t \,\hat{\mathbf{k}}\).

Responder

\(=2π\)Unidades de longitud

8) Encuentra la longitud del arco de la función valorada por vector\(\vecs r(t)=−t \,\hat{\mathbf{i}}+4t \,\hat{\mathbf{j}}+3t \,\hat{\mathbf{k}}\) sobre\([0,1]\).

9) Una partícula viaja en círculo con la ecuación de movimiento\(\vecs r(t)=3 \cos t \,\hat{\mathbf{i}}+3 \sin t \,\hat{\mathbf{j}} +0 \,\hat{\mathbf{k}}\). Encuentra la distancia recorrida alrededor del círculo por la partícula.

Responder

\(6π\)unidades

10) Establecer una integral para encontrar la circunferencia de la elipse con la ecuación\(\vecs r(t)= \cos t \,\hat{\mathbf{i}}+2 \sin t \,\hat{\mathbf{j}}+0\,\hat{\mathbf{k}}\).

11) Encuentra la longitud de la curva\(\vecs r(t)=⟨\sqrt{2}t,\, e^t, \, e^{−t}⟩\) a lo largo del intervalo\(0≤t≤1\). El gráfico se muestra aquí:

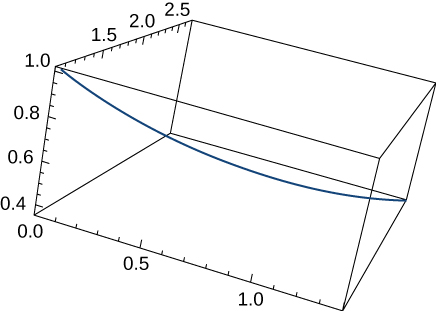
Responder

\(\left(e−\frac{1}{e}\right)\)unidades

12) Encuentra la longitud de la curva\(\vecs r(t)=⟨2 \sin t, \, 5t, \, 2 \cos t⟩\) para\(t∈[−10,10]\).

Vectores de tangentes unitarios y vectores normales unitarios

13) La función de posición para una partícula es\(\vecs r(t)=a \cos( ωt) \,\hat{\mathbf{i}}+b \sin (ωt) \,\hat{\mathbf{j}}\). Encuentre el vector tangente unitario y el vector normal unitario en\(t=0\).

Solución:

\ (\ begin {align*}\ vecs r' (t) &= -aω\ sin (ωt)\,\ hat {\ mathbf {i}} +bω\ cos (ωt)\,\ hat {\ mathbf {j}}\\ [5pt]
\ |\ vecs r' (t)\ | &=\ sqrt {a^2 ω^2\ sin^2 (ωt) +b^2ω^2\ cos^2 (ωt)}\\ [5pt]
\ vecs T (t) &=\ dfrac {\ vecs r' (t)} {\ |\ vecs r' (t)\ |} =\ dfrac {-aω\ sin (ωt)\,\ hat {\ mathbf {i}} +bω\ cos (ωt)\,\ hat {\ mathbf {j}}} {\ sqrt {a^2 ω^2\ sin^2 (ωt) +b^2ω^2\ cos^2 (ωt)}}\\ [5pt]
\ vecs T (0) &=\ dfrac {bω\,\ hat {\ mathbf {j}}} {\ sqrt {(bω) ^2}} =\ dfrac {bω\,\ hat {\ mathbf {j}}} {|bω|}\ end {align*}\)

Si\(bω > 0, \; \vecs T(0) = \hat{\mathbf{j}},\) y si\( bω < 0, \; T(0)= -\hat{\mathbf{j}}\)

Responder

Si\(bω > 0, \; \vecs T(0)= \hat{\mathbf{j}},\) y si\( bω < 0, \; \vecs T(0)= -\hat{\mathbf{j}}\)

Si\(a > 0, \; \vecs N(0)= -\hat{\mathbf{i}},\) y si\( a < 0, \; \vecs N(0)= \hat{\mathbf{i}}\)

14) Dado\(\vecs r(t)=a \cos (ωt) \,\hat{\mathbf{i}} +b \sin (ωt) \,\hat{\mathbf{j}}\), encontrar el vector binormal\(\vecs B(0)\).

15) Dado\(\vecs r(t)=⟨2e^t,e^t \cos t,e^t \sin t⟩\), determinar el vector tangente unitario\(\vecs T(t)\).

Responder

\ (\ begin {align*}\ vecs T (t) &=\ izquierda\ langle\ frac {2} {\ sqrt {6}},\,\ frac {\ cos t−\ sin t} {\ sqrt {6}},\,\ frac {\ cos t+\ sin t} {\ sqrt {6}}\ derecha\ rangle\\ [4pt]
=\ izquierda\ langle\ frac {\ sqrt {6}} {3},\,\ frac {\ sqrt {6}} {6} (\ cos t−\ sin t),\,\ frac {\ sqrt {6}} {6} (\ cos t+\ sin t)\ derecha\ rangle\ final { alinear*}\)

16) Dado\(\vecs r(t)=⟨2e^t,\, e^t \cos t,\, e^t \sin t⟩\), encontrar el vector tangente unitario\(\vecs T(t)\) evaluado en\(t=0\),\(\vecs T(0)\).

17) Dado\(\vecs r(t)=⟨2e^t,\, e^t \cos t,\, e^t \sin t⟩\), determinar el vector normal unitario\(\vecs N(t)\).

Responder

\(\vecs N(t)=⟨0,\, -\frac{\sqrt{2}}{2} (\sin t + \cos t), \, \frac{\sqrt{2}}{2} (\cos t- \sin t)⟩\)

18) Dado\(\vecs r(t)=⟨2e^t,\, e^t \cos t,\, e^t \sin t⟩\), encontrar el vector normal unitario\(\vecs N(t)\) evaluado en\(t=0\),\(\vecs N(0)\).

Responder

\(\vecs N(0)=⟨0, \;-\frac{\sqrt{2}}{2},\;\frac{\sqrt{2}}{2}⟩\)

19) Dado\(\vecs r(t)=t \,\hat{\mathbf{i}}+t^2 \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\), encontrar el vector tangente unitario\(\vecs T(t)\). El gráfico se muestra aquí:

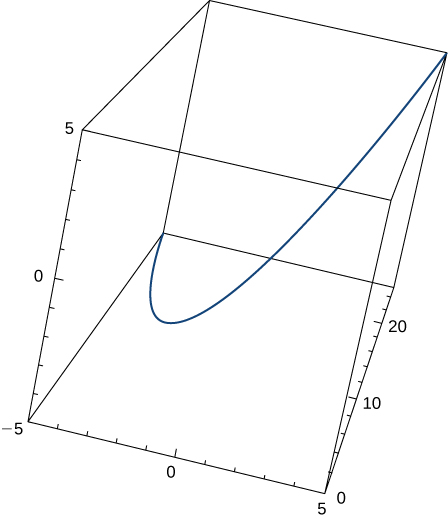
Responder

\(\vecs T(t)=\dfrac{1}{\sqrt{4t^2+2}}<1,2t,1>\)

20) Encuentre el vector tangente unitario\(\vecs T(t)\) y el vector normal unitario\(\vecs N(t)\) en\(t=0\) para la curva plana\(\vecs r(t)=⟨t^3−4t,5t^2−2⟩\). El gráfico se muestra aquí:

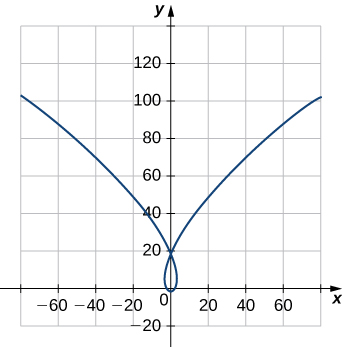
21) Encuentra el vector tangente unitario\(\vecs T(t)\) para\(\vecs r(t)=3t \,\hat{\mathbf{i}}+5t^2 \,\hat{\mathbf{j}}+2t \,\hat{\mathbf{k}}\).

Responder

\(\vecs T(t)=\dfrac{1}{\sqrt{100t^2+13}}(3 \,\hat{\mathbf{i}}+10t \,\hat{\mathbf{j}}+2 \,\hat{\mathbf{k}})\)

22) Encontrar el vector normal principal a la curva\(\vecs r(t)=⟨6 \cos t,6 \sin t⟩\) en el punto determinado por\(t=\frac{π}{3}\).

23) Encuentra\(\vecs T(t)\) para la curva\(\vecs r(t)=(t^3−4t) \,\hat{\mathbf{i}}+(5t^2−2) \,\hat{\mathbf{j}}\).

Responder

\(\vecs T(t)=\dfrac{1}{\sqrt{9t^4+76t^2+16}}\big((3t^2−4)\,\hat{\mathbf{i}}+10t \,\hat{\mathbf{j}}\big)\)

24) Encuentra\(\vecs N(t)\) para la curva\(\vecs r(t)=(t^3−4t)\,\hat{\mathbf{i}}+(5t^2−2)\,\hat{\mathbf{j}}\).

25) Encuentra el vector tangente unitario\(\vecs T(t)\) para\(\vecs r(t)=⟨2 \sin t,\, 5t,\, 2 \cos t⟩\).

Responder

\(\vecs T(t)=⟨\frac{2\sqrt{29}}{29}\cos t,\, \frac{5\sqrt{29}}{29},\,−\frac{2\sqrt{29}}{29}\sin t⟩\)

26) Encuentra el vector normal de la unidad\(\vecs N(t)\) para\(\vecs r(t)=⟨2\sin t,\,5t,\,2\cos t⟩\).

Responder

\(\vecs N(t)=⟨−\sin t,\, 0,\, −\cos t⟩\)

Parameterizaciones de Longitud de Arco

27) Encuentra la función de longitud de arco\(\vecs s(t)\) para el segmento de línea dado por\(\vecs r(t)=⟨3−3t,\, 4t⟩\). Después escribe la parametrización de longitud de arco de\(r\) with\(s\) como parámetro.

Responder

Función de longitud de arco:\(s(t)=5t\); La parametrización de longitud de arco de\(\vecs r(t)\):\(\vecs r(s)=\left(3−\dfrac{3s}{5}\right)\,\hat{\mathbf{i}}+\dfrac{4s}{5}\,\hat{\mathbf{j}}\)

28) Parametrizar la hélice\(\vecs r(t)= \cos t \,\hat{\mathbf{i}}+ \sin t \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\) usando el parámetro de longitud de arco\(s\), de\(t=0\).

29) Parametrizar la curva usando el parámetro de longitud de arco\(s\), en el punto en el que\(t=0\) para\(\vecs r(t)=e^t \sin t \,\hat{\mathbf{i}} + e^t \cos t \,\hat{\mathbf{j}}\)

Responder

\(\vecs r(s)=\left(1+\dfrac{s}{\sqrt{2}}\right) \sin \left( \ln \left(1+ \dfrac{s}{\sqrt{2}}\right)\right)\,\hat{\mathbf{i}} +\left(1+ \dfrac{s}{\sqrt{2}}\right) \cos \left( \ln \left(1+\dfrac{s}{\sqrt{2}}\right)\right)\,\hat{\mathbf{j}}\)

Curvatura y Círculo Osculante

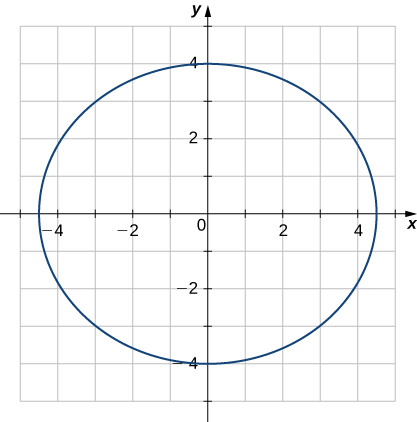
30) Encuentra la curvatura de la curva\(\vecs r(t)=5 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf{j}}\) en\(t=π/3\). (Nota: La gráfica es una elipse.)

31) Encuentra la\(x\) coordenada en la que la curvatura de la curva\(y=1/x\) es un valor máximo.

Responder

El valor máximo de la curvatura se produce en\(x=1\).

32) Encuentra la curvatura de la curva\(\vecs r(t)=5 \cos t \,\hat{\mathbf{i}}+5 \sin t \,\hat{\mathbf{j}}\). ¿La curvatura depende del parámetro\(t\)?

33) Encuentra la curvatura\(κ\) de la curva\(y=x−\frac{1}{4}x^2\) en el punto\(x=2\).

Responder

\(\frac{1}{2}\)

34) Encuentra la curvatura\(κ\) para la curva\(y=\frac{1}{3}x^3\) en el punto\(x=1\).

35) Encuentra la curvatura\(κ\) de la curva\(\vecs r(t)=t \,\hat{\mathbf{i}}+6t^2 \,\hat{\mathbf{j}}+4t \,\hat{\mathbf{k}}\). El gráfico se muestra aquí:

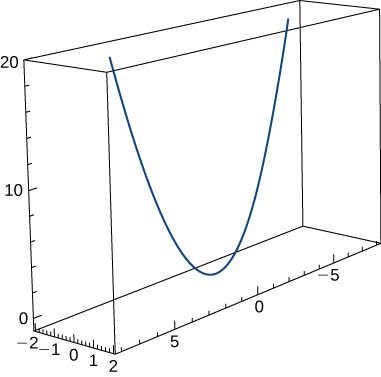
Responder

\(κ≈\dfrac{49.477}{(17+144t^2)^{3/2}}\)

36) Encuentra la curvatura de\(\vecs r(t)=⟨2 \sin t,5t,2 \cos t⟩\).

37) Encuentra la curvatura de\(\vecs r(t)=\sqrt{2}t \,\hat{\mathbf{i}}+e^t \,\hat{\mathbf{j}}+e^{−t} \,\hat{\mathbf{k}}\) en el punto\(P(0,1,1)\).

Responder

\(\frac{1}{2\sqrt{2}}\)

38) ¿En qué punto tiene la curva\(y=e^x\) la curvatura máxima?

39) ¿Qué pasa con la curvatura en\(x→∞\) cuanto a la curva\(y=e^x\)?

Responder

La curvatura se aproxima a cero.

40) Encuentra el punto de curvatura máxima en la curva\(y=\ln x\).

41) Encontrar las ecuaciones del plano normal y el plano osculante de la curva\(\vecs r(t)=⟨2 \sin (3t),t,2 \cos (3t)⟩\) en punto\((0,π,−2)\).

Responder

\(y=6x+π\)y\(x+6y=6π\)

42) Encuentra ecuaciones de los círculos osculantes de la elipse\(4y^2+9x^2=36\) en los puntos\((2,0)\) y\((0,3)\).

43) Encuentra la ecuación para el plano osculante en el punto\(t=π/4\) de la curva\(\vecs r(t)=\cos (2t) \,\hat{\mathbf{i}}+ \sin (2t) \,\hat{\mathbf{j}}+t\,\hat{\mathbf{k}}\).

Responder

\(x+2z=\frac{π}{2}\)

44) Encontrar el radio de curvatura de\(6y=x^3\) en el punto\((2,\frac{4}{3}).\)

45) Encuentra la curvatura en cada punto de\((x,y)\) la hipérbola\(\vecs r(t)=⟨a \cosh( t),b \sinh (t)⟩\).

Responder

\(\dfrac{a^4b^4}{(b^4x^2+a^4y^2)^{3/2}}\)

46) Calcular la curvatura de la hélice circular\(\vecs r(t)=r \sin (t) \,\hat{\mathbf{i}}+r \cos (t) \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\).

47) Encontrar el radio de curvatura de\(y= \ln (x+1)\) en el punto\((2,\ln 3)\).

Responder

\(\frac{10\sqrt{10}}{3}\)

48) Encontrar el radio de curvatura de la hipérbola\(xy=1\) en el punto\((1,1)\).

Una partícula se mueve a lo largo de la curva plana\(C\) descrita por\(\vecs r(t)=t \,\hat{\mathbf{i}}+t^2 \,\hat{\mathbf{j}}\). Utilice esta parametrización para responder a las preguntas 49 - 51.

49) Encuentra la longitud de la curva a lo largo del intervalo\([0,2]\).

Responder

\(\frac{1}{4}\big[ 4\sqrt{17} + \ln\left(4+\sqrt{17}\right)\big]\text{ units }\approx 4.64678 \text{ units}\)

50) Encuentra la curvatura de la curva plana en\(t=0,1,2\).

51) Describir la curvatura a medida que t aumenta de\(t=0\) a\(t=2\).

Responder

La curvatura disminuye a lo largo de este intervalo.

La superficie de una copa grande se forma girando la gráfica de la función\(y=0.25x^{1.6}\) de\(x=0\) a\(x=5\) alrededor del\(y\) eje -eje (medido en centímetros).

52) [T] Utilice la tecnología para graficar la superficie.

53) Encontrar la curvatura\(κ\) de la curva generadora en función de\(x\).

Contestar

\(κ=\dfrac{30}{x^{2/5}\left(25+4x^{6/5}\right)^{3/2}}\)

Ten en cuenta que inicialmente tu respuesta puede ser:
\(\dfrac{6}{25x^{2/5}\left(1+\frac{4}{25}x^{6/5}\right)^{3/2}}\)

Podemos simplificarlo de la siguiente manera:
\ (\ begin {align*}\ dfrac {6} {25x^ {2/5}\ left (1+\ frac {4} {25} x^ {6/5}\ right) ^ {3/2}} &=\ dfrac {6} {25x^ {2/ 5}\ grande [\ frac {1} {25}\ izquierda (25+4x^ {6/5}\ derecha)\ grande] ^ {3/2}}\\ [4pt]
&=\ dfrac {6} {25x^ {2/5}\ izquierda (\ frac {1} {25}\ derecha) ^ {3/2}\ grande [25+4x^ {6/5}\ grande ^ {3/2}}\\ [4pt]
&=\ dfrac {6} {\ frac {25} {125} x^ {2/5}\ grande [25+4x^ {6/5}\ grande] ^ {3/2}}\\ [4pt]
&=\ dfrac {30} {x^ {2/ 5}\ izquierda (25+4x^ {6/5}\ derecha) ^ {3/2}}\ final {alinear*}\)

54) [T] Utilice la tecnología para graficar la función de curvatura.

Colaboradores:

• Template:ContribOpenStaxCalc
• Paul Seeburger (Monroe Community College) created question 6.