14.4: Planos tangentes y aproximaciones lineales

Objetivos de aprendizaje

• Determinar la ecuación de un plano tangente a una superficie dada en un punto.
• Utilice el plano tangente para aproximar una función de dos variables en un punto.
• Explicar cuando una función de dos variables es diferenciable.
• Utilice el diferencial total para aproximar el cambio en una función de dos variables.

En esta sección, consideramos el problema de encontrar el plano tangente a una superficie, lo cual es análogo a encontrar la ecuación de una línea tangente a una curva cuando la curva es definida por la gráfica de una función de una variable,\( y=f(x)\). La pendiente de la línea tangente en el punto\( x=a\) viene dada por\( m=f′(a)\); ¿cuál es la pendiente de un plano tangente? Aprendimos sobre la ecuación de un plano en Ecuaciones de Líneas y Planos en el Espacio; en esta sección, vemos cómo se puede aplicar al problema que nos ocupa.

Planos tangentes

Intuitivamente, parece claro que, en un plano, sólo una línea puede ser tangente a una curva en un punto. Sin embargo, en el espacio tridimensional, muchas líneas pueden ser tangentes a un punto dado. Si estas líneas se encuentran en el mismo plano, determinan el plano tangente en ese punto. Una forma más intuitiva de pensar en un plano tangente es asumir que la superficie es lisa en ese punto (sin esquinas). Entonces, una línea tangente a la superficie en ese punto en cualquier dirección no tiene ningún cambio abrupto en la pendiente porque la dirección cambia suavemente. Por lo tanto, en un vecindario lo suficientemente pequeño alrededor del punto, un plano tangente toca la superficie solo en ese punto.

Definición: líneas tangentes

Dejar\( P_0=(x_0,y_0,z_0)\) ser un punto en una superficie\( S\), y dejar que\( C\) sea cualquier curva que pase a través\( P_0\) y que quede completamente adentro\( S\). Si las líneas tangentes a todas esas curvas se\( P_0\) encuentran\( C\) en el mismo plano, entonces este plano se llama el plano tangente a\( S\) at\( P_0\) (Figura\(\PageIndex{1}\)).

Figura\(\PageIndex{1}\): El plano tangente a una superficie\( S\) en un punto\( P_0\) contiene todas las líneas tangentes a las curvas en\(S\) ese paso\( P_0\).

Para que un plano tangente a una superficie exista en un punto de esa superficie, es suficiente que la función que define la superficie sea diferenciable en ese punto. Definimos el término plano tangente aquí y luego exploramos la idea de manera intuitiva.

Definición: planos tangentes

Dejar\( S\) ser una superficie definida por una función diferenciable\( z=f(x,y),\) y dejar\( P_0=(x_0,y_0)\) ser un punto en el dominio de\( f\). Entonces, la ecuación del plano tangente a\( S\) at\( P_0\) viene dada por

\[z=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0). \label{tanplane} \]

Para ver por qué esta fórmula es correcta, primero busquemos dos líneas tangentes a la superficie\( S\). La ecuación de la línea tangente a la curva que se representa por la intersección de\( S\) con la traza vertical dada por\( x=x_0\) es\( z=f(x_0,y_0)+f_y(x_0,y_0)(y−y_0)\). De igual manera, la ecuación de la línea tangente a la curva que se representa por la intersección de\( S\) con la traza vertical dada por\( y=y_0\) es\( z=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)\). Un vector paralelo a la primera línea tangente es\( \vecs a=\,\hat{\mathbf j}+f_y(x_0,y_0)\,\hat{\mathbf k}\); un vector paralelo a la segunda línea tangente es\(\vecs b=\hat{\mathbf i}+f_x(x_0,y_0)\,\hat{\mathbf k}\). Podemos tomar el producto cruzado de estos dos vectores:

\[\begin{align*} \vecs a\times \vecs b &=(\,\hat{\mathbf j}+f_y(x_0,y_0)\,\hat{\mathbf k})×(\,\hat{\mathbf i}+f_x(x_0,y_0)\,\hat{\mathbf k})\\[4pt] &=\begin{vmatrix}\hat{\mathbf i} & \hat{\mathbf j} & \hat{\mathbf k}\\[4pt] 0 & 1 & f_y(x_0,y_0)\\[4pt] 1 & 0 & f_x(x_0,y_0)\end{vmatrix} \\[4pt] &=f_x(x_0,y_0)\,\hat{\mathbf i}+f_y(x_0,y_0)\,\hat{\mathbf j}−\,\hat{\mathbf k}. \end{align*}\]

Este vector es perpendicular a ambas líneas y por lo tanto es perpendicular al plano tangente. Podemos usar este vector como un vector normal al plano tangente, junto con el punto\( P_0=(x_0,y_0,f(x_0,y_0))\) en la ecuación para un plano:

\[ \begin{align*}\vecs n·((x−x_0)\,\hat{\mathbf i}+(y−y_0)\,\hat{\mathbf j}+(z−f(x_0,y_0))\,\hat{\mathbf k}) &=0 \\[4pt] (f_x(x_0,y_0)\,\hat{\mathbf i}+f_y(x_0,y_0)\,\hat{\mathbf j}-\,\hat{\mathbf k})·((x−x_0)\,\hat{\mathbf i}+(y−y_0)\,\hat{\mathbf j}+(z−f(x_0,y_0))\,\hat{\mathbf k}) &=0 \\[4pt] f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)−(z−f(x_0,y_0)) &=0. \end{align*}\]

Resolviendo esta ecuación para\(z\) da Ecuación\ ref {tanplane}.

Ejemplo\( \PageIndex{1}\): Finding a Tangent Plane

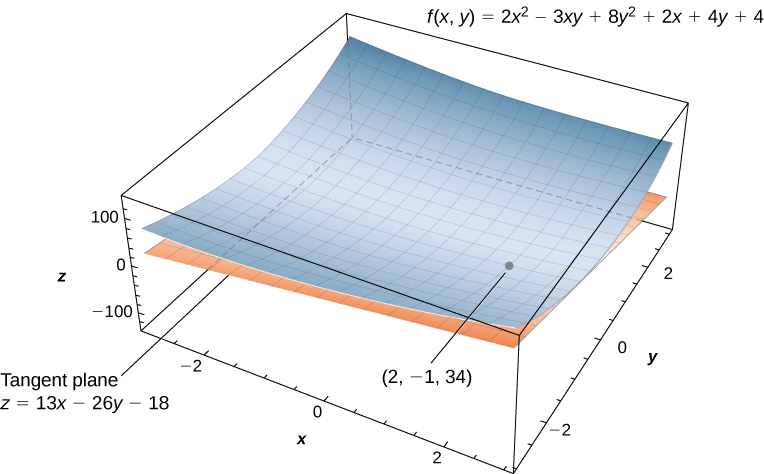
Encontrar la ecuación del plano tangente a la superficie definida por la función\( f(x,y)=2x^2−3xy+8y^2+2x−4y+4\) en el punto\( (2,−1).\)

Solución

Primero, debemos calcular\( f_x(x,y)\) y\( f_y(x,y)\), luego usar Ecuación con\( x_0=2\) y\( y_0=−1\):

\[\begin{align*} f_x(x,y) &=4x−3y+2 \\[4pt] f_y(x,y) &=−3x+16y−4 \\[4pt] f(2,−1) &=2(2)^2−3(2)(−1)+8(−1)^2+2(2)−4(−1)+4=34 \\[4pt] f_x(2,−1) &=4(2)−3(−1)+2=13 \\[4pt] f_y(2,−1) &=−3(2)+16(−1)−4=−26.\end{align*}\]

Entonces la Ecuación\ ref {tanplane} se convierte

\[\begin{align*} z &=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0) \\[4pt] z &=34+13(x−2)−26(y−(−1)) \\[4pt] z &=34+13x−26−26y−26 \\[4pt] z &=13x−26y−18. \end{align*}\]

(Ver la siguiente figura).

Figura\(\PageIndex{2}\): Calcular la ecuación de un plano tangente a una superficie dada en un punto dado.

Ejercicio\( \PageIndex{1}\)

Encuentra la ecuación del plano tangente a la superficie definida por la función\( f(x,y)=x^3−x^2y+y^2−2x+3y−2\) en punto\( (−1,3)\).

Insinuación

Primero, calcule\( f_x(x,y)\) y\( f_y(x,y)\), luego use la Ecuación\ ref {tanplane}.

Contestar

\( z=7x+8y−3\)

Ejemplo\( \PageIndex{2}\): Finding Another Tangent Plane

Encuentra la ecuación del plano tangente a la superficie definida por la función\( f(x,y)=\sin(2x)\cos(3y)\) en el punto\( (π/3,π/4).\)

Solución

Primero, calcule\( f_x(x,y)\) y\( f_y(x,y)\), luego use la ecuación\ ref {tanplane} con\( x_0=π/3\) y\( y_0=π/4\):

\[\begin{align*} f_x(x,y) &=2\cos(2x)\cos(3y) \\[4pt] f_y(x,y) &=−3\sin(2x)\sin(3y) \\[4pt] f\left(\dfrac{π}{3},\dfrac{π}{4}\right) &=\sin\left(2\left(\dfrac{π}{3}\right)\right)\cos\left(3\left(\dfrac{π}{4}\right)\right)=\left(\dfrac{\sqrt{3}}{2}\right)\left(−\dfrac{\sqrt{2}}{2}\right)=−\dfrac{\sqrt{6}}{4} \\[4pt] f_x\left(\dfrac{π}{3},\dfrac{π}{4}\right) &=2\cos\left(2\left(\dfrac{π}{3}\right)\right)\cos\left(3\left(\dfrac{π}{4}\right)\right)=2\left(−\dfrac{1}{2}\right)\left(−\dfrac{\sqrt{2}}{2}\right)=\dfrac{\sqrt{2}}{2} \\[4pt] f_y \left(\dfrac{π}{3},\dfrac{π}{4}\right) &=−3\sin\left(2\left(\dfrac{π}{3}\right)\right)\sin\left(3\left(\dfrac{π}{4}\right)\right)=−3\left(\dfrac{\sqrt{3}}{2}\right)\left(\dfrac{\sqrt{2}}{2}\right)=−\dfrac{3\sqrt{6}}{4}. \end{align*}\]

Entonces la Ecuación\ ref {tanplane} se convierte

\[\begin{align*} z &=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0) \\[4pt] &=−\dfrac{\sqrt{6}}{4}+\dfrac{\sqrt{2}}{2}\left(x−\dfrac{π}{3}\right)−\dfrac{3\sqrt{6}}{4}\left(y−\dfrac{π}{4}\right) \\[4pt] &=\dfrac{\sqrt{2}}{2}x−\dfrac{3\sqrt{6}}{4}y−\dfrac{\sqrt{6}}{4}−\dfrac{π\sqrt{2}}{6}+\dfrac{3π\sqrt{6}}{16} \end{align*}\]

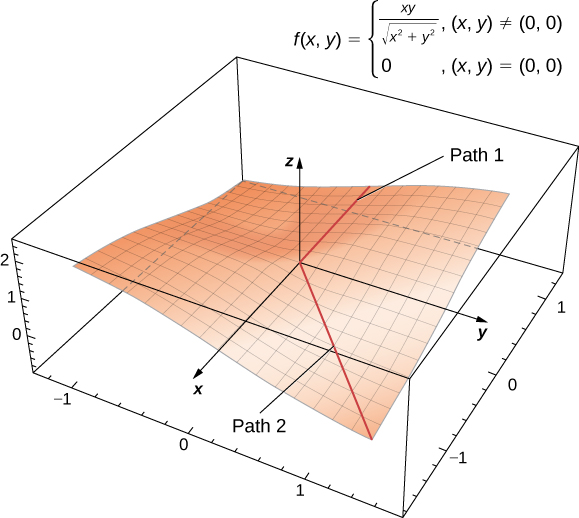
Un plano tangente a una superficie no siempre existe en todos los puntos de la superficie. Considere la función por piezas

\[f(x,y)=\begin{cases}\dfrac{xy}{\sqrt{x^2+y^2}}, & & (x,y)≠(0,0)\\[4pt] 0, & & (x,y)=(0,0)\end{cases}. \label{oddfunction} \]

A continuación se muestra la gráfica de esta función.

Figura\(\PageIndex{3}\): Gráfica de una función que no tiene un plano tangente en el origen. Figura dinámica impulsada por CalcPlot3D.

Si cualquiera\( x=0\) o\( y=0\),\( f(x,y)=0,\) entonces entonces el valor de la función no cambia en el eje\(x\) - o\(y\) -. Por lo tanto\( f_x(x,0)=f_y(0,y)=0\), para que ya sea\( x\) o se\( y\) acerque a cero, estas derivadas parciales permanecen iguales a cero. Sustituyéndolos en Ecuación da\( z=0\) como la ecuación de la línea tangente. No obstante, si nos acercamos al origen desde una dirección diferente, obtenemos una historia diferente. Por ejemplo, supongamos que nos acercamos al origen a lo largo de la línea\( y=x\). Si ponemos\( y=x\) en la función original, se convierte

\[f(x,x)=\dfrac{x(x)}{\sqrt{x^2+(x)^2}}=\dfrac{x^2}{\sqrt{2x^2}}=\dfrac{|x|}{\sqrt{2}}. \nonumber \]

Cuando\( x>0,\) la pendiente de esta curva es igual a\( \sqrt{2}/2\); cuando\( x<0\), la pendiente de esta curva es igual a\( −(\sqrt{2}/2).\) Esto presenta un problema. En la definición de plano tangente, presumimos que todas las líneas tangentes a través del punto\( P\) (en este caso, el origen) yacían en el mismo plano. Claramente este no es el caso aquí. Cuando estudiemos funciones diferenciables, veremos que esta función no es diferenciable en el origen.

Aproximaciones Lineales

Recordemos de aproximaciones lineales y diferenciales que la fórmula para la aproximación lineal de una función\( f(x)\) en el punto\( x=a\) viene dada por

\[y≈f(a)+f'(a)(x−a). \nonumber \]

El diagrama para la aproximación lineal de una función de una variable aparece en la siguiente gráfica.

Figura\(\PageIndex{4}\): Aproximación lineal de una función en una variable.

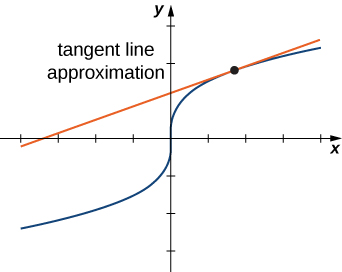
La línea tangente se puede utilizar como una aproximación a la función\( f(x)\) para valores\( x\) razonablemente cercanos a\( x=a\). Cuando se trabaja con una función de dos variables, la línea tangente es reemplazada por un plano tangente, pero la idea de aproximación es muy parecida.

Definición: Aproximación lineal

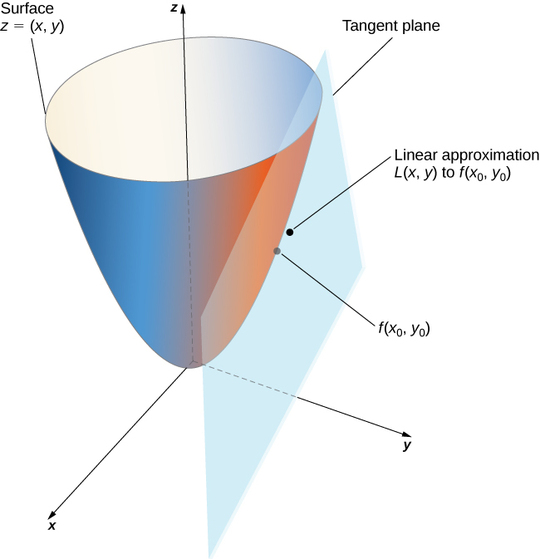
Dada una función\( z=f(x,y)\) con derivadas parciales continuas que existen en el punto\( (x_0,y_0)\), la aproximación lineal de\(f\) en el punto\( (x_0,y_0)\) viene dada por la ecuación

\[L(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0). \label{approx} \]

Observe que esta ecuación también representa el plano tangente a la superficie definida por\( z=f(x,y)\) en el punto\( (x_0,y_0)\). La idea detrás del uso de una aproximación lineal es que, si hay un punto\( (x_0,y_0)\) en el que\( f(x,y)\) se conoce el valor preciso de, entonces para valores\( (x,y)\) razonablemente cercanos a\( (x_0,y_0)\), la aproximación lineal (es decir, plano tangente) produce un valor que también es razonablemente cercano al valor exacto de\( f(x,y)\) (Figura). Además, el plano que se utiliza para encontrar la aproximación lineal es también el plano tangente a la superficie en el punto\( (x_0,y_0).\)

Figura\(\PageIndex{5}\): Uso de un plano tangente para aproximación lineal en un punto.

Ejemplo\( \PageIndex{3}\): Using a Tangent Plane Approximation

Dada la función\( f(x,y)=\sqrt{41−4x^2−y^2}\), aproximado\( f(2.1,2.9)\) usando punto\( (2,3)\) para\( (x_0,y_0).\) ¿Cuál es el valor aproximado de\( f(2.1,2.9)\) a cuatro decimales?

Solución

Para aplicar la Ecuación\ ref {approx}, primero debemos calcular\( f(x_0,y_0), f_x(x_0,y_0),\) y\( f_y(x_0,y_0)\) usar\( x_0=2\) y\( y_0=3:\)

\[\begin{align*} f(x_0,y_0) &=f(2,3)=\sqrt{41−4(2)^2−(3)^2}=\sqrt{41−16−9}=\sqrt{16}=4 \\[4pt] f_x(x,y) &=−\dfrac{4x}{\sqrt{41−4x^2−y^2}} \text{ so} \; f_x(x_0,y_0)=−\dfrac{4(2)}{\sqrt{41−4(2)^2−(3)^2}}=−2 \\[4pt] f_y(x,y) &=−\dfrac{y}{\sqrt{41−4x^2−y^2}} \text{ so}\; f_y(x_0,y_0)=−\dfrac{3}{\sqrt{41−4(2)^2−(3)^2}}=−\dfrac{3}{4}. \end{align*}\]

Ahora sustituimos estos valores en Ecuación\ ref {approx}:

\[\begin{align*} L(x,y) &=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0) \\[4pt] &=4−2(x−2)−\dfrac{3}{4}(y−3) \\[4pt] &=\dfrac{41}{4}−2x−\dfrac{3}{4}y. \end{align*}\]

Por último, sustituimos\( x=2.1\) y\( y=2.9\) en\(L(x,y):\)

\[ L(2.1,2.9)=\dfrac{41}{4}−2(2.1)−\dfrac{3}{4}(2.9)=10.25−4.2−2.175=3.875. \nonumber \]

El valor aproximado de\( f(2.1,2.9)\) a cuatro decimales es

\[ f(2.1,2.9)=\sqrt{41−4(2.1)^2−(2.9)^2}=\sqrt{14.95}≈3.8665, \nonumber \]

lo que corresponde a un\( 0.2%\) error de aproximación.

Ejercicio\( \PageIndex{2}\)

Dada la función\( f(x,y)=e^{5−2x+3y},\) aproximada\( f(4.1,0.9)\) usando punto\( (4,1)\) para\( (x_0,y_0)\). ¿Cuál es el valor aproximado de\( f(4.1,0.9)\) a cuatro decimales?

Insinuación

Primero calcule\( f(x_0,y_0),f_x(x_0,y_0),\) y\( f_y(x_0,y_0)\) use\( x_0=4\) y\( y_0=1\), luego use la ecuación\ ref {approx}.

Contestar

\( L(x,y)=6−2x+3y,\)por lo\( L(4.1,0.9)=6−2(4.1)+3(0.9)=0.5\)\( f(4.1,0.9)=e^{5−2(4.1)+3(0.9)}=e^{−0.5}≈0.6065.\)

Diferenciabilidad

Cuando se trabaja con una función\( y=f(x)\) de una variable, se dice que la función es diferenciable en un punto\( x=a\) si\( f′(a)\) existe. Además, si una función de una variable es diferenciable en un punto, la gráfica es “suave” en ese punto (es decir, no existen esquinas) y una línea tangente está bien definida en ese punto.

La idea detrás de la diferenciabilidad de una función de dos variables está conectada con la idea de suavidad en ese punto. En este caso, se considera que una superficie es lisa en el punto\( P\) si existe un plano tangente a la superficie en ese punto. Si una función es diferenciable en un punto, entonces existe un plano tangente a la superficie en ese punto. Recordemos la fórmula (Ecuación\ ref {tanplane}) para un plano tangente en un punto\( (x_0,y_0)\) viene dada por

\[z=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0) \nonumber \]

Para que exista un plano tangente en el punto\( (x_0,y_0),\) las derivadas parciales deben existir, por lo tanto, en ese punto. Sin embargo, esta no es una condición suficiente para la suavidad, como se ilustra en la Figura. En ese caso, las derivadas parciales existían en el origen, pero la función también tenía una esquina en la gráfica en el origen.

Definición: Funciones diferenciables

Una función\( f(x,y)\) es diferenciable en un punto\( P(x_0,y_0)\) si, para todos los puntos\( (x,y)\) en un\( δ\) disco alrededor\( P\), podemos escribir

\[f(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)+E(x,y), \label{diff1} \]

donde el término de error\( E\) satisface

\[\lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}=0. \label{diff2} \]

El último término en la Ecuación\ ref {diff1} es como el término de error y representa cuán cerca llega el plano tangente a la superficie en una pequeña vecindad (\( δ\)disco) de punto\( P\). Para\( f\) que la función sea diferenciable en\( P\), la función debe ser suave, es decir, la gráfica de\( f\) debe estar cerca del plano tangente para los puntos cercanos\( P\).

Ejemplo\( \PageIndex{4}\): Demonstrating Differentiability

Demostrar que la función\( f(x,y)=2x^2−4y\) es diferenciable en el punto\( (2,−3).\)

Solución

Primero, calculamos\( f(x_0,y_0),f_x(x_0,y_0),\) y\( f_y(x_0,y_0)\) usamos\( x_0=2\) y\( y_0=−3,\) luego usamos la ecuación\ ref {diff1}:

\[\begin{align*} f(2,−3) &=2(2)^2−4(−3)=8+12=20 \\[4pt] f_x(2,−3) &=4(2)=8 \\[4pt] f_y(2,−3) &=−4. \end{align*}\]

Por lo tanto\( m_1=8\)\( m_2=−4,\) y y la Ecuación\ ref {diff1} se convierte

\[ \begin{align*} f(x,y) &=f(2,−3)+f_x(2,−3)(x−2)+f_y(2,−3)(y+3)+E(x,y) \\[4pt] 2x^2−4y &=20+8(x−2)−4(y+3)+E(x,y) \\[4pt] 2x^2−4y &=20+8x−16−4y−12+E(x,y) \\[4pt] 2x^2−4y &=8x−4y−8+E(x,y) \\[4pt] E(x,y) &=2x^2−8x+8. \end{align*}\]

A continuación, calculamos el límite en la Ecuación\ ref {diff2}:

\ [\ begin {alinear*}\ lim_ {(x, y) → (x_0, y_0)}\ dfrac {E (x, y)} {\ sqrt {(x−x+0) ^2+ (y−y_0) ^2}} &=\ lim_ {(x, y) → (2, −3)}\ dfrac {2x^2−+8} {\ sqrt {(x−2) ^2+ (y+3) ^2}}\\ [4pt]
&=\ lim_ {(x, y) → (2, −3)}\ dfrac {2 (x^2−4x+4)} {\ sqrt {(x−2) ^2+ (y+3) ^2}}\\ [4pt]
&=\ lim_ (x, y) → (2, −3)}\ dfrac {2 (x−2) ^2} {\ sqrt {(x −2) ^2+ (y+3) ^2}}\\ [4pt]
&=\ lim_ {(x, y) → (2, −3)}\ dfrac {2 ((x−2) ^2+ (y+3) ^2)} {\ sqrt {(x−2) ^2+ (y+3) ^2}}\\ [4pt]
&=\ lim_ {(x, y) → (2, −3)} 2\ sqrt {(x−2) ^2+ (y+3) ^2}\\ [4pt]
&=0. \ end {alinear*}\]

Ya que\( E(x,y)≥0\) para cualquier valor de\( x\) o\( y\), el límite original debe ser igual a cero. Por lo tanto,\( f(x,y)=2x^2−4y\) es diferenciable en el punto\( (2,−3)\).

Ejercicio\( \PageIndex{3}\)

Demostrar que la función\( f(x,y)=3x−4y^2\) es diferenciable en el punto\((−1,2)\).

Insinuación

Primero, calcula\( f(x_0,y_0),f_x(x_0,y_0),\) y\( f_y(x_0,y_0)\) usa\( x_0=−1\) y\( y_0=2\), luego usa la ecuación\ ref {diff2} para encontrar\( E(x,y)\). Por último, calcule el límite.

Contestar

\ [\ begin {alinear*} f (−1,2) &=−19,\ quad f_x (−1,2) =3,\ quad f_y (−1,2) =−16,\ quad E (x, y) =−4 (y−2) ^2.\\ [4pt]
\ lim_ {(x, y) → (x_0, y_0)}\ dfrac {E (x, y)} {\ sqrt {(x−x_0) ^2+ (y−y_0) ^2}} &=\ lim_ {(x, y) → (−1,2)}\ dfrac {−4 (y−2) ^2} {\ sqrt {(x+1) ^2+ (y−2) ^2}}\\ [4pt]
&≤\ lim_ (x, y) → (−1,2)}\ dfrac {−4 ((x+1) ^2+ (y−2) ^2)} {\ sqrt {(x+1) ^2+ (y−2) ^2}}\\ [4pt]
&=\ lim_ {(x, y) → (2, −3)} −4\ sqrt {(x+1) ^2+ (y−2) ^2}\\ [4pt]
=0. \ end {alinear*}\]

Esta función de (Ecuación\ ref {oddfunction})

\[ f(x,y)=\begin{cases}\dfrac{xy}{\sqrt{x^2+y^2}}, & & (x,y)≠(0,0)\\[4pt] 0, & & (x,y)=(0,0)\end{cases} \nonumber \]

no es diferenciable en el origen (Figura\(\PageIndex{3}\)). Esto lo podemos ver calculando las derivadas parciales. Esta función apareció anteriormente en la sección, donde lo demostramos\( f_x(0,0)=f_y(0,0)=0\). Sustituyendo esta información en Ecuaciones\ ref {diff1} y\ ref {diff2} usando\( x_0=0\) y\( y_0=0\), obtenemos

\[\begin{align*} f(x,y) &=f(0,0)+f_x(0,0)(x−0)+f_y(0,0)(y−0)+E(x,y) \\[4pt] E(x,y) &=\dfrac{xy}{\sqrt{x^2+y^2}}. \end{align*}\]

Calculando

\[ \lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}} \nonumber \]

da

\[\begin{align*} \lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}} &=\lim_{(x,y)→(0,0)}\dfrac{\dfrac{xy}{\sqrt{x^2+y^2}}}{\sqrt{x^2+y^2}} \\[4pt] &=\lim_{(x,y)→(0,0)}\dfrac{xy}{x^2+y^2}. \end{align*}\]

Dependiendo del camino que se tome hacia el origen, este límite toma diferentes valores. Por lo tanto, el límite no existe y la función no\( f\) es diferenciable en el origen como se muestra en la siguiente figura.

Figura\(\PageIndex{6}\): Esta función\( f(x,y)\) (Ecuación\ ref {oddfunction}) no es diferenciable en el origen.

Se conectan diferenciabilidad y continuidad para funciones de dos o más variables, lo mismo que para funciones de una variable. De hecho, con algunos ajustes de notación, el teorema básico es el mismo.

TEOREMA: Diferenciabilidad Implica Continuidad

Dejar\( z=f(x,y)\) ser una función de dos variables con\( (x_0,y_0)\) en el dominio de\( f\). Si\( f(x,y)\) es diferenciable en\( (x_0,y_0)\), entonces\( f(x,y)\) es continuo en\( (x_0,y_0).\)

Nota muestra que si una función es diferenciable en un punto, entonces es continua ahí. Sin embargo, si una función es continua en un punto, entonces no es necesariamente diferenciable en ese punto. Por ejemplo, la función discutida anteriormente (Ecuación\ ref {oddfunction})

\[f(x,y)=\begin{cases}\dfrac{xy}{\sqrt{x^2+y^2}}, & & (x,y)≠(0,0)\\[4pt] 0, & & (x,y)=(0,0)\end{cases} \nonumber \]

es continuo en el origen, pero no es diferenciable en el origen. Esta observación también es similar a la situación en el cálculo de una sola variable.

Podemos explorar más a fondo la conexión entre continuidad y diferenciabilidad en un punto. Este siguiente teorema dice que si la función y sus derivadas parciales son continuas en un punto, la función es diferenciable.

Teorema: La continuidad de los primeros parciales implica diferenciabilidad

Dejar\( z=f(x,y)\) ser una función de dos variables con\( (x_0,y_0)\) en el dominio de\( f\). Si\(f(x,y)\),\(f_x(x,y)\), y\(f_y(x,y)\) todos existen en un barrio de\((x_0,y_0)\) y son continuos en\((x_0,y_0)\), entonces\(f(x,y)\) es diferenciable ahí.

Recordemos que antes demostramos que la función en Ecuación\ ref {oddfunction} no era diferenciable en el origen. Calculemos las derivadas parciales\( f_x\) y\( f_y\):

\[ \dfrac{∂f}{∂x}=\dfrac{y^3}{(x^2+y^2)^{3/2}} \nonumber \]

y

\[\dfrac{∂f}{∂y}=\dfrac{x^3}{(x^2+y^2)^{3/2}}. \nonumber \]

El contrapositivo del teorema anterior establece que si una función no es diferenciable, entonces al menos una de las hipótesis debe ser falsa. Exploremos la condición que\( f_x(0,0)\) debe ser continua. Para que esto sea cierto, debe ser cierto que

\[ \lim_{(x,y)→(0,0)} f_x(x,y)=f_x(0,0) \nonumber \]

por lo tanto

\[ \lim_{(x,y)→(0,0)}f_x(x,y)=\lim_{(x,y)→(0,0)}\dfrac{y^3}{(x^2+y^2)^{3/2}}. \nonumber \]

Vamos\( x=ky\). Entonces

\ [\ begin {alinear*}\ lim_ {(x, y) → (0,0)}\ dfrac {y^3} {(x^2+y^2) ^ {3/2}} &=\ lim_ {y→0}\ dfrac {y^3} {((ky) ^2+y^2) ^ {3/2}}\\ [4pt]
&=\ lim_ {y→0}\ dfrac {y^3} {(k^2y^2+y^2) ^ {3/2}}\\ [4pt]
&=\ lim_ {y→0}\ dfrac {y^3} {|y|^3 (k^2+1) ^ {3/2}}\\ [4pt] &=\ dfrac {1} {(k^2+1) ^ {(k^2}}\\ [4pt]
&=\ dfrac {1} {(k^^2+1) ^ {3/2}}\ lim_ {y →0}\ dfrac {|y|} {y}. \ end {alinear*}\]

Si\( y>0\), entonces esta expresión es igual\( 1/(k^2+1)^{3/2}\); si\( y<0\), entonces es igual\( −(1/(k^2+1)^{3/2})\). En cualquier caso, el valor depende de\( k\), por lo que el límite no existe.

Diferenciales

En Aproximaciones Lineales y Diferenciales estudiamos primero el concepto de diferenciales. El diferencial de\( y\), escrito\( dy\), se define como\( f′(x)dx\). El diferencial se utiliza para aproximar\( Δy=f(x+Δx)−f(x)\), donde\( Δx=dx\). Al extender esta idea a la aproximación lineal de una función de dos variables en el punto se\( (x_0,y_0)\) obtiene la fórmula para el diferencial total para una función de dos variables.

Definición: Diferencial Total

Dejar\( z=f(x,y)\) ser una función de dos variables con\( (x_0,y_0)\) en el dominio de\( f\), y dejar\( Δx\) y\( Δy\) ser elegido para que también\( (x_0+Δx,y_0+Δy)\) esté en el dominio de\( f\). Si\( f\) es diferenciable en el punto\( (x_0,y_0)\), entonces los diferenciales\( dx\) y\( dy\) se definen como

\[dx=Δx \nonumber \]

y

\[dy=Δy. \nonumber \]

El diferencial\( dz\), también llamado diferencial total de\( z=f(x,y)\) at\( (x_0,y_0)\), se define como

\[dz=f_x(x_0,y_0)dx+f_y(x_0,y_0)dy. \label{total} \]

Observe que el símbolo no\( ∂\) se utiliza para denotar el diferencial total; más bien,\( d\) aparece frente a\( z\). Ahora, vamos a definir\( Δz=f(x+Δx,y+Δy)−f(x,y).\) Utilizamos\( dz\) para aproximar\( Δz\), entonces

\[Δz≈dz=f_x(x_0,y_0)dx+f_y(x_0,y_0)dy. \nonumber \]

Por lo tanto, el diferencial se utiliza para aproximar el cambio en la función\( z=f(x_0,y_0)\) en el punto\( (x_0,y_0)\) para valores dados de\( Δx\) y\( Δy\). Ya que\( Δz=f(x+Δx,y+Δy)−f(x,y)\), esto se puede utilizar más para aproximarse\( f(x+Δx,y+Δy):\)

\[ f(x+Δx,y+Δy)=f(x,y)+Δz≈f(x,y)+fx(x_0,y_0)Δx+f_y(x_0,y_0)Δy. \nonumber \]

Consulte la siguiente figura.

Figura\(\PageIndex{7}\): La aproximación lineal se calcula a través de la fórmula\( f(x+Δx,y+Δy)≈f(x,y)+f_x(x_0,y_0)Δx+f_y(x_0,y_0)Δy.\)

Una de esas aplicaciones de esta idea es determinar la propagación de errores. Por ejemplo, si estamos fabricando un gadget y estamos apagados en cierta cantidad al medir una cantidad dada, el diferencial puede usarse para estimar el error en el volumen total del gadget.

Ejemplo\( \PageIndex{5}\): Approximation by Differentials

Encuentra el diferencial\( dz\) de la función\( f(x,y)=3x^2−2xy+y^2\) y úsalo para aproximar\( Δz\) en el punto\( (2,−3).\) Uso\( Δx=0.1\) y\( Δy=−0.05.\) ¿Cuál es el valor exacto de\( Δz\)?

Solución

Primero, debemos calcular\( f(x_0,y_0),f_x(x_0,y_0),\) y\( f_y(x_0,y_0)\) usar\( x_0=2\) y\( y_0=−3:\)

\[\begin{align*} f(x_0,y_0) &=f(2,−3)=3(2)^2−2(2)(−3)+(−3)^2=12+12+9=33 \\[4pt] f_x(x,y) &=6x−2y \\[10pt] f_y(x,y) &=−2x+2y \\[4pt] f_x(x_0,y_0) &= fx(2,−3) \\[4pt] &=6(2)−2(−3)=12+6=18 \\[10pt] f_y(x_0,y_0) &=f_y(2,−3) \\[4pt] &=−2(2)+2(−3) \\[4pt] &=−4−6=−10. \end{align*}\]

Luego, sustituimos estas cantidades en la Ecuación\ ref {total}:

\[\begin{align*} dz &=f_x(x_0,y_0)dx+f_y(x_0,y_0)dy \\[4pt] dz &=18(0.1)−10(−0.05)=1.8+0.5=2.3. \end{align*}\]

Esta es la aproximación a\( Δz=f(x_0+Δx,y_0+Δy)−f(x_0,y_0).\) El valor exacto de\( Δz\) viene dado por

\[\begin{align*} Δz &=f(x_0+Δx,y_0+Δy)−f(x_0,y_0) \\[4pt] &=f(2+0.1,−3−0.05)−f(2,−3) \\[4pt] &=f(2.1,−3.05)−f(2,−3) \\[4pt] &=2.3425. \end{align*}\]

Ejercicio\( \PageIndex{4}\)

Encuentra el diferencial\( dz\) de la función\( f(x,y)=4y^2+x^2y−2xy\) y úsalo para aproximarlo\( Δz\) en el punto\( (1,−1)\). Uso\( Δx=0.03\) y\( Δy=−0.02\). ¿Cuál es el valor exacto de\( Δz\)?

Insinuación

Primero, calcule\( f_x(x_0,y_0)\) y\( f_y(x_0,y_0)\) use\( x_0=1\) y\( y_0=−1\), luego use la Ecuación\ ref {total}.

Contestar

\( dz=0.18\)

\( Δz=f(1.03,−1.02)−f(1,−1)=0.180682\)

Diferenciabilidad de una función de tres variables

Todos los resultados anteriores para la diferenciabilidad de funciones de dos variables pueden generalizarse a funciones de tres variables. En primer lugar, la definición:

Definición: Diferenciabilidad en un punto

Una función\( f(x,y,z)\) es diferenciable en un punto\( P(x_0,y_0,z_0)\) si para todos los puntos\( (x,y,z)\) en un\( δ\) disco alrededor\( P\) podemos escribir

\[f(x,y)=f(x_0,y_0,z_0)+f_x(x_0,y_0,z_0)(x−x_0)+f_y(x_0,y_0,z_0)(y−y_0)+f_z(x_0,y_0,z_0)(z−z_0)+E(x,y,z), \nonumber \]

donde el término de error E satisface

\[\lim_{(x,y,z)→(x_0,y_0,z_0)}\dfrac{E(x,y,z)}{\sqrt{(x−x_0)^2+(y−y_0)^2+(z−z_0)^2}}=0. \nonumber \]

Si una función de tres variables es diferenciable en un punto\( (x_0,y_0,z_0)\), entonces ahí es continua. Además, la continuidad de las primeras derivadas parciales en ese punto garantiza la diferenciabilidad.

Conceptos clave

• El análogo de una línea tangente a una curva es un plano tangente a una superficie para funciones de dos variables.
• Los planos tangentes se pueden utilizar para aproximar valores de funciones cerca de valores conocidos.
• Una función es diferenciable en un punto si es “suave” en ese punto (es decir, no existen esquinas ni discontinuidades en ese punto).
• El diferencial total se puede utilizar para aproximar el cambio en una función\( z=f(x_0,y_0)\) en el punto\( (x_0,y_0)\) para valores dados de\( Δx\) y\( Δy\).

Ecuaciones Clave

• Plano tangente

\( z=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)\)

• Aproximación lineal

\( L(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)\)

• Diferencial total

\( dz=f_x(x_0,y_0)dx+f_y(x_0,y_0)dy\).

• Diferenciabilidad (dos variables)

\( f(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)+E(x,y),\)

donde el término de error\( E\) satisface

\(\displaystyle \lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}=0\).

• Diferenciabilidad (tres variables)

\( f(x,y)=f(x_0,y_0,z_0)+f_x(x_0,y_0,z_0)(x−x_0)+f_y(x_0,y_0,z_0)(y−y_0)+f_z(x_0,y_0,z_0)(z−z_0)+E(x,y,z),\)

donde el término de error\( E\) satisface

\(\displaystyle \lim_{(x,y,z)→(x_0,y_0,z_0)}\dfrac{E(x,y,z)}{\sqrt{(x−x_0)^2+(y−y_0)^2+(z−z_0)^2}}=0\).

Glosario

diferenciable

una función\( f(x,y)\) es diferenciable en\( (x_0,y_0)\) si se\( f(x,y)\) puede expresar en la forma\( f(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)+E(x,y),\)

donde el término de error\( E(x,y)\) satisface\( \lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}=0\)

aproximación lineal

dada una función\( f(x,y)\) y un plano tangente a la función en un punto\( (x_0,y_0)\), podemos aproximarnos\( f(x,y)\) para los puntos cercanos\( (x_0,y_0)\) usando la fórmula del plano tangente

plano tangente

dada una función\( f(x,y)\) que es diferenciable en un punto\( (x_0,y_0)\), la ecuación del plano tangente a la superficie\( z=f(x,y)\) viene dada por\( z=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)\)

diferencial total

el diferencial total de la función\( f(x,y)\) at\( (x_0,y_0)\) viene dado por la fórmula\( dz=f_x(x_0,y_0)dx+fy(x_0,y_0)dy\)