14.4E: Ejercicios para la Sección 14.4

Última actualización
Guardar como PDF

Page ID: 116209

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En los ejercicios 1 - 2, encuentra un vector normal unitario a la superficie en el punto indicado.

1)$ f(x,y)=x^3,\quad (2,−1,8)$

Contestar: $ (\frac{\sqrt{145}}{145})(12\hat{\mathbf i}−\hat{\mathbf k})$

2)$ \ln\left(\dfrac{x}{y−z}\right)=0$ cuando$ x=y=1$

En los ejercicios 3 - 7, encuentra un vector normal y un vector tangente en el punto$ P$.

3)$ x^2+xy+y^2=3,\quad P(−1,−1)$

Contestar: Vector normal:$ \hat{\mathbf i}+\hat{\mathbf j}$, vector tangente:$ \hat{\mathbf i}−\hat{\mathbf j}$

4)$ (x^2+y^2)^2=9(x^2−y^2),\quad P(\sqrt{2},1)$

5)$ xy^2−2x^2+y+5x=6,\quad P(4,2)$

Contestar: Vector normal:$ 7\hat{\mathbf i}−17\hat{\mathbf j}$, vector tangente:$ 17\hat{\mathbf i}+7\hat{\mathbf j}$

6)$ 2x^3−x^2y^2=3x−y−7,\quad P(1,−2)$

7)$ ze^{x^2−y^2}−3=0, \quad P(2,2,3)$

Contestar: Vector normal:$ -12\hat{\mathbf i}+12\hat{\mathbf j}-\hat{\mathbf k}$ o$ 12\hat{\mathbf i}-12\hat{\mathbf j}+\hat{\mathbf k}$, Vector
tangente:$ 0\hat{\mathbf i}+1\hat{\mathbf j}+12\hat{\mathbf k}$ o$ 1\hat{\mathbf i}+0\hat{\mathbf j}-12\hat{\mathbf k}$

En los ejercicios 8 - 19, encuentra la ecuación para el plano tangente a la superficie en el punto indicado. (Pista: Si la función dada no está ya resuelta para$z$, comience por resolverla$ z$ en términos de$ x$ y$ y$.)

8)$ −8x−3y−7z=−19,\quad P(1,−1,2)$

9)$ z=−9x^2−3y^2,\quad P(2,1,−39)$

Contestar: $ −36x−6y−z=−39$

10)$ x^2+10xyz+y^2+8z^2=0,\quad P(−1,−1,−1)$

11)$ z=\ln(10x^2+2y^2+1),\quad P(0,0,0)$

Contestar: $ z=0$

12)$ z=e^{7x^2+4y^2}, \quad P(0,0,1)$

13)$ xy+yz+zx=11,\quad P(1,2,3)$

Contestar: $ 5x+4y+3z−22=0$

14)$ x^2+4y^2=z^2,\quad P(3,2,5)$

15)$ x^3+y^3=3xyz,\quad P(1,2,\frac{3}{2})$

Contestar: $ 4x−5y+4z=0$

16)$ z=axy,\quad P(1,\frac{1}{a},1)$

17)$ z=\sin x+\sin y+\sin(x+y),\quad P(0,0,0)$

Contestar: $ 2x+2y−z=0$

18)$ h(x,y)=\ln\sqrt{x^2+y^2},\quad P(3,4)$

19)$ z=x^2−2xy+y^2,\quad P(1,2,1)$

Contestar: $ −2(x−1)+2(y−2)−(z−1)=0$

En los ejercicios 20 - 25, encuentra ecuaciones paramétricas para la línea normal a la superficie en el punto indicado. (Recordemos que para encontrar la ecuación de una línea en el espacio, se necesita un punto en la línea$ P_0(x_0,y_0,z_0)$,, y un vector$ \vecs v=⟨a,b,c⟩$ que sea paralelo a la línea. Entonces las ecuaciones de la línea son:$\quad x=x_0+at,\quad y=y_0+bt, \quad z=z_0+ct.)$

20)$ −3x+9y+4z=−4,\quad P(1,−1,2)$

21)$ z=5x^2−2y^2,\quad P(2,1,18)$

Contestar: $ x=20t+2,y=−4t+1,z=−t+18$

22)$ x^2−8xyz+y^2+6z^2=0,\quad P(1,1,1)$

23)$ z=\ln(3x^2+7y^2+1),\quad P(0,0,0)$

Contestar: $ x=0,y=0,z=t$

24)$ z=e^{4x^2+6y^2},\quad P(0,0,1)$

25)$ z=x^2−2xy+y^2$ en el punto$ P(1,2,1)$

Contestar: $ x−1=2t;y−2=−2t;z−1=t$

En los ejercicios 26 - 28, utilice la figura que se muestra aquí.

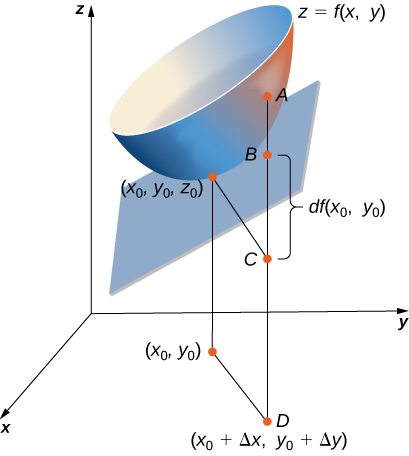
$Diagrama que muestra el diferencial de f en el punto (x_0, y_0)$

26) ¿La longitud del segmento de línea$ AC$ es igual a qué expresión matemática?

27) ¿La longitud del segmento de línea$ BC$ es igual a qué expresión matemática?

Contestar: El diferencial de la función$ z(x,y)=dz=f_xdx+f_ydy$

28) Usando la figura, explica lo que$ AB$ representa la longitud del segmento de línea.

29) Demostrar que$ f(x,y)=e^{xy}x$ es diferenciable en el punto$ (1,0).$

Contestar: Usando la definición de diferenciabilidad, tenemos$ e^{xy}x≈x+y$.

30) Demostrar que$ f(x,y)=x^2+3y$ es diferenciable en cada punto. En otras palabras, mostrar que$ Δz=f(x+Δx,y+Δy)−f(x,y)=f_xΔx+f_yΔy+ε_1Δx+ε_2Δy$, donde ambos$ ε_1$ y$ ε_2$ acercarse a cero como se$ (Δx,Δy)$ acerca$ (0,0).$

Contestar: $ Δz=2xΔx+3Δy+(Δx)^2.(Δx)^2→0$para pequeños$ Δx$ y$ z$ satisface la definición de diferenciabilidad.

31) Encuentra el diferencial total de cada función:

$ z=x^3 + y^3 - 5$
$ z=e^{xy}$
$ z=y\cos x+\sin y$
$P = t^2 + 3t + tu^3$
$ w=e^y\cos(x)+z^2$

Respuestas:

$ dz = 3x^2\,dx +3y^2\,dy $
$ dz = ye^{xy}\,dx +xe^{xy}\,dy $
$ dz = -y\sin x\,dx +(\cos x + \cos y)\,dy $
$ dP = (2t + 3 + u^3)\, dt + 3t u^2 \,du $
$ dw = -e^y\sin(x)\,dx +e^y\cos(x)\,dy +2z\,dz$

32) a. Encontrar el diferencial total$dz$ de la función$ z=\dfrac{xy}{y+x}$ y luego
b. Indicar su valor donde$ x$ cambia de$ 10$ a$ 10.5$ y$ y$ cambia de$ 15$ a$ 13$.

Contestar: a.$ dz = \dfrac{y^2}{(x+y)^2}\, dx + \dfrac{x^2}{(x+y)^2} \,dy $
b.$dx = 0.5$ y$dy = -2$ así

\ (\ begin {align*} dz &= f_x (10, 15)\, dx + f_y (10,15)\, dy\\
&=\ frac {15^2} {25^2}\, dx +\ frac {10^2} {25^2}\, dy\\
&=\ frac {225} {625}\, (0.5) +\ frac {100} { 625} (-2)\\
&=\ frac {9} {25}\ izquierda (\ frac {1} {2}\ derecha) +\ frac {4} {25} (-2)\\
&=\ frac {18} {100} -\ frac {32} {100}\
&= .18 - .32 = -0.14\ final {alinear*}\)

33) Vamos a$ z=f(x,y)=xe^y.$ exponer su diferencial total. Después computa$ Δz$ de$ P(1,2)$ a$ Q(1.05,2.1)$ y luego encuentra el cambio aproximado en$ z$,$dz$, de punto$ P$ a punto$ Q$. Recordar$ Δz=f(x+Δx,y+Δy)−f(x,y)$,$ dz$ y y$ Δz$ debe ser aproximadamente igual, si$dx$ y$dy$ son ambos razonablemente pequeños.

Contestar: Diferencial Total:$dz = e^y\,dx + xe^y\, dy $
$ Δz≈1.185422$ y$ dz≈1.108.$ Tenga en cuenta que están relativamente cerca.

34) El volumen de un cilindro circular derecho viene dado por$ V(r,h)=πr^2h.$ Encuentra el diferencial$ dV$. Interpretar la fórmula geométricamente.

Contestar: $ dV = 2 \pi r h\, dr + \pi r^2 \,dh $

35) Ver el problema anterior. Utilice diferenciales para estimar la cantidad de aluminio en una lata de aluminio encerrada con diámetro$ 8.0cm$ y altura$ 12cm$ si el aluminio tiene$ 0.04$ cm de espesor.

Contestar: $ 16\,\text{cm}^3$

36) Usa el diferencial$ dz$ para aproximar el cambio en a$ z=\sqrt{4−x^2−y^2}$ medida que$ (x,y)$ se mueve de punto$ (1,1)$ a punto$ (1.01,0.97).$ Compara esta aproximación con el cambio real en la función.

37) Dejar$ z=f(x,y)=x^2+3xy−y^2.$ Encontrar el cambio exacto en la función y el cambio aproximado en la función como$ x$ cambios de$ 2.00$ a$ 2.05$ y$ y$ cambios de$ 3.00$ a$ 2.96$.

Contestar: $ Δz=$cambio exacto$ =0.6449$, cambio aproximado es$ dz=0.65$. Los dos valores son cercanos.

38) La aceleración centrípeta de una partícula que se mueve en un círculo viene dada por$ a(r,v)=\frac{v^2}{r},$ donde$ v$ está la velocidad y$ r$ es el radio del círculo. Aproximar el porcentaje máximo de error en la medición de la aceleración resultante de errores de$ 3\%$ in$ v$ y$ 2\%$ in$ r$. (Recordemos que el error porcentual es la relación entre la cantidad de error sobre la cantidad original. Entonces, en este caso, el porcentaje de error en a viene dado por$ \frac{da}{a}$.)

39) El radio$ r$ y la altura$ h$ de un cilindro circular derecho se miden con posibles errores de$ 4\%$ y$ 5\%$, respectivamente. Aproximar el error porcentual máximo posible en la medición del volumen (Recordemos que el error porcentual es la relación entre la cantidad de error sobre la cantidad original. Entonces, en este caso, el porcentaje de error en$ V$ viene dado por$ \frac{dV}{V}$.)

Contestar: $ 13\%$o$ 0.13$

40) El radio base y la altura de un cono circular derecho se miden como$ 10$ en. y$ 25$ in., respectivamente, con un posible error en la medición de tanto como$ 0.1$ en. cada uno. Utilice diferenciales para estimar el error máximo en el volumen calculado del cono.

41) La resistencia eléctrica$ R$ producida por resistencias de cableado$ R_1$ y$ R_2$ en paralelo se puede calcular a partir de la fórmula$ \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}$. Si$ R_1$ y$ R_2$ se miden para ser$ 7Ω$ y$ 6Ω$, respectivamente, y si estas mediciones son precisas dentro$ 0.05Ω$, estime el máximo error posible en la computación$ R$. (El símbolo$ Ω$ representa un ohmio, la unidad de resistencia eléctrica.)

Contestar: $ 0.025$

42) El área de una elipse con ejes de longitud$ 2a$ y$ 2b$ viene dada por la fórmula$ A=πab$. Aproximar el porcentaje de cambio en el área cuando$ a$ aumenta en$ 2\%$ y$ b$ aumenta en$ 1.5\%.$

43) El periodo$ T$ de un péndulo simple con pequeñas oscilaciones se calcula a partir de la fórmula$ T=2π\sqrt{\frac{L}{g}}$, donde$ L$ está la longitud del péndulo y$ g$ es la aceleración resultante de la gravedad. Supongamos que$ L$ y$ g$ tienen errores de, a lo sumo,$ 0.5\%$ y$ 0.1\%$, respectivamente. Utilice diferenciales para aproximar el porcentaje máximo de error en el valor calculado de$ T$.

Contestar: $ 0.3\%$

44)$ P$ La energía eléctrica viene dada por$ P=\frac{V^2}{R}$, donde$ V$ esta el voltaje y$ R$ es la resistencia. Aproximar el porcentaje máximo de error en el cálculo de la potencia si$ 120 V$ se aplica a una$ 2000−Ω$ resistencia y los posibles errores porcentuales en la medición$ V$ y$ R$ son$ 3\%$ y$ 4\%$, respectivamente.

Para los ejercicios 45 - 49, encuentra la aproximación lineal de cada función en el punto indicado.

45)$ f(x,y)=x\sqrt{y},\quad P(1,4)$

Contestar: $ L(x,y) = 2x+\frac{1}{4}y−1$

46)$ f(x,y)=e^x\cos y;\quad P(0,0)$

47)$ f(x,y)=\arctan(x+2y),\quad P(1,0)$

Contestar: $ L(x,y) = \frac{1}{2}x+y+\frac{1}{4}π−\frac{1}{2}$

48)$ f(x,y)=\sqrt{20−x^2−7y^2},\quad P(2,1)$

49)$ f(x,y,z)=\sqrt{x^2+y^2+z^2},\quad P(3,2,6)$

Contestar: $ L(x,y,z) = \frac{3}{7}x+\frac{2}{7}y+\frac{6}{7}z$

50) [T] Encuentra la ecuación del plano tangente a la superficie$ f(x,y)=x^2+y^2$ en el punto$ (1,2,5),$ y grafica la superficie y el plano tangente en el punto.

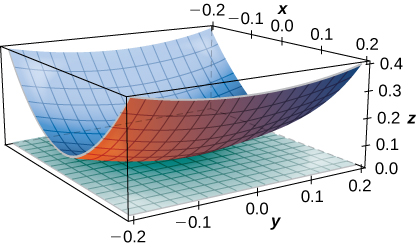
51) [T] Encuentra la ecuación para el plano tangente a la superficie en el punto indicado, y grafica la superficie y el plano tangente:$ z=\ln(10x^2+2y^2+1),\quad P(0,0,0).$

Contestar

$ z=0$

$Superficie que representa la función z=ln (10x^2+2y^2+1) y su plano tangente en el punto (0, 0)$

52) [T] Encuentra la ecuación del plano tangente a la superficie$ z=f(x,y)=\sin(x+y^2)$ en el punto$ \left(\frac{π}{4},0,\frac{\sqrt{2}}{2}\right)$, y grafica la superficie y el plano tangente.

Colaboradores

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) created all but part e of exercise 31.